PASAPORTE MATEMATICAS 2 BIMESTRE 2

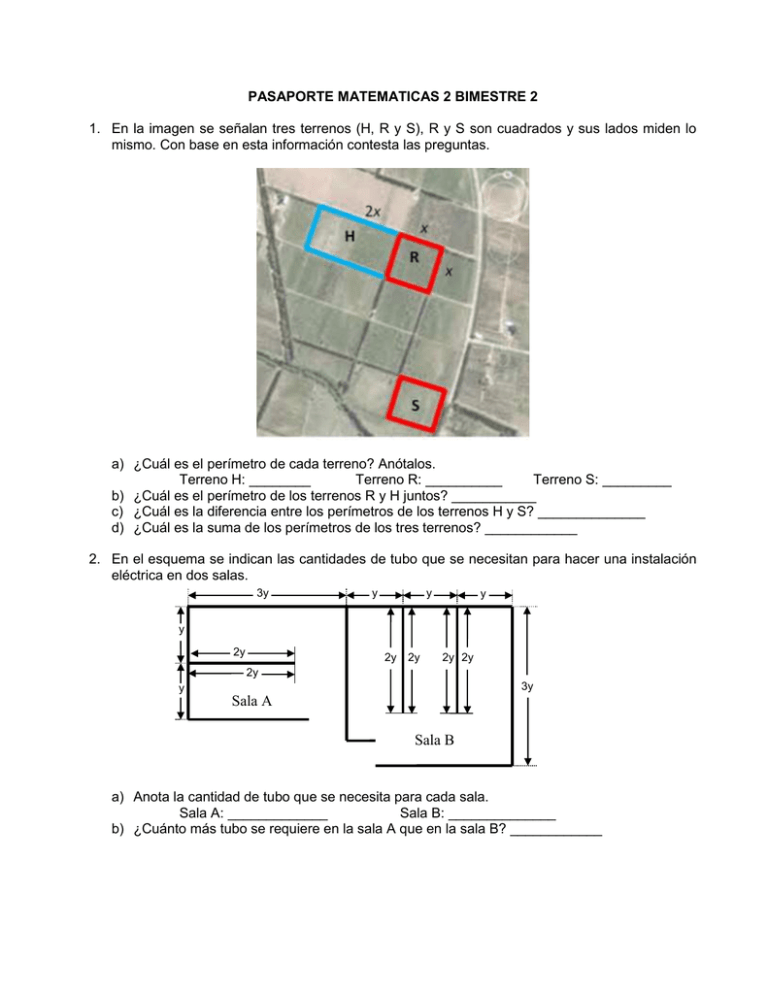
PASAPORTE MATEMATICAS 2 BIMESTRE 2
1. En la imagen se señalan tres terrenos (H, R y S), R y S son cuadrados y sus lados miden lo
mismo. Con base en esta información contesta las preguntas.
a) ¿Cuál es el perímetro de cada terreno? Anótalos.
Terreno H: ________
Terreno R: __________
Terreno S: _________
b) ¿Cuál es el perímetro de los terrenos R y H juntos? ___________
c) ¿Cuál es la diferencia entre los perímetros de los terrenos H y S? ______________
d) ¿Cuál es la suma de los perímetros de los tres terrenos? ____________
2. En el esquema se indican las cantidades de tubo que se necesitan para hacer una instalación
eléctrica en dos salas.
3y
y
y
y
y
2y
2y
2y
2y 2y
2y
3y
y
Sala A
Sala B
a) Anota la cantidad de tubo que se necesita para cada sala.
Sala A: _____________
Sala B: ______________
b) ¿Cuánto más tubo se requiere en la sala A que en la sala B? ____________
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1. ¿Cuál es la expresión algebraica que representa el perímetro de cada polígono que se
muestra?
3.21z
4.44z
1
3 z
2
1
4 z
3
2.91z
3.58z
1
3 z
4
1
4.31z
1
z
10
1
2 z
5
3.43z
2. Un decágono regular y un rectángulo tienen igual perímetro. Tracen ambas figuras y anoten las
medidas de los lados sabiendo que el perímetro de cada figura es 10x.
3.-¿Cuál es el
perímetro de la siguiente figura?
w
4
1.3w
3w
2
1.3w
4.-¿Cuál es el perímetro de las siguientes figuras?
a
x
x
x
x
a
a
x
n
a
P = ________
m
m
P = ________
n
n
P = ________
5.-Expresen de manera general y simplificada, cada una de las siguientes situaciones:
a) La suma de tres números consecutivos _______________________________
b) La suma de cuatro números consecutivos ______________________________
c) La suma de cinco números consecutivos _______________________________
6.-¿Cuál es el perímetro de cada una de las siguientes figuras?
3a + 5
5x - 2
2x
2x – 1
3x + 2
7.-Pedro compró 8 cuadernos a n pesos cada uno, si al pagar le descontaron el precio de 2 cuadernos
¿Cuánto pagó?
8.-Rosa y Tere fueron al supermercado, Rosa compró 3 kg de manzanas y Tere compró 2 kg de
manzanas y 3 kg de uvas. Cada una pagó con un billete de $100.00. Si el kilogramo de manzanas
cuesta n pesos, y el de uvas m pesos, ¿Cuánto recibió de cambio cada una?
Encuentren la expresión algebraica que representa el área de las siguientes figuras:
m
m
n
n
m
A = __________
A=___________
n
A=___________
Representen algebraicamente las áreas de las siguientes figuras tomando como base las
anteriores:
a)
m
A = ___________________________
m
m
n
b)
n
m
n
c)
m
n
n
A = ___________________________
n
m
A = ___________________________
m
n
n
m
1. Una fábrica produce azulejos de tres tamaños diferentes. Las dimensiones de los
azulejos son como las que se muestran enseguida:
a
a
1
1
1
a
a) Representen algebraicamente las áreas de las siguientes figuras formadas con
azulejos:
Figura 1
Figura 2

4
4
a
a + 1
A= ______________
1
A= ________________
Figura 3
Figura 4
2
2

2
2
a + 1
A= _______________
a
1
A= _________________
1
Figura 6
Figura 5

a
a
a
a
+ 2
A= __________________
2
A= ____________________
b) ¿Qué relación observaron entre las áreas de cada par de figuras?
c) ¿Se puede afirmar, entonces, lo mismo para sus respectivas expresiones
algebraicas?
d) Si se sustituye la literal “a” en cada figura por un valor determinado (2, 3 ó 4) ¿cómo
son los resultados en cada caso?
Dados los siguientes patrones de figuras; construir para cada expresión algebraica, dos
modelos diferentes de figuras geométricas y expresar algebraicamente sus áreas.
Figura 2
Figura 1
m
Figura 3
m
n
m
a) 3m 2  2m n
b) 2m 2  2n 2  mn
n
n
REALIZA LAS OPERACIONES.
n(n  4) 
4x 2  2x 
2x 2  x 
2a 2  ab 
Expresen el volumen de los siguientes cuerpos.
3cm
3cm
3cm
V=
V=
V=
15
12
10
3cm
2cm
7
V=
V=
4cm
V=
3a
V=
a
a
c
V=
Se puede obtener el volumen de estos cuerpos geométricos empleando las fórmulas que
aparecen abajo? digan por qué.
Cubo
V = l3
Prismas
V= ABh
(lado al cubo)
(Área de la base x altura)
Armen los desarrollos planos de los prismas que se encuentran abajo. Cuiden dejar una
cara del prisma cuadrangular sin pegar.
Una vez armados los cuerpos, calculen su volumen. Expliquen su procedimiento.
a) Recorten el desarrollo plano de la pirámide que está enseguida y peguen sus caras
cuidando dejar la base sin pegar.
b) Comparen la pirámide que acaban de armar y el prisma cuadrangular que armaron
antes y señalen semejanzas y diferencias.
c) Llenen la pirámide con sal y vacíen el contenido en el prisma cuadrangular anterior,
háganlo tantas veces como sea necesario para llenar el prisma. Al terminar de
hacer esto contesten las siguientes preguntas.
◊ ¿Cuántas veces vaciaron el contenido completo de la pirámide en el prisma?
◊ ¿Qué relación habrá entre lo que hicieron y la fórmula para calcular el
volumen de una pirámide (V = ABh o V = 1/3 ABh )?
3
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1.- A un cubo le caben 3 375 cm3 de agua, ¿cuánto miden las aristas del cubo?
2.- Si se duplica la medida de las aristas del cubo:
a) ¿Qué cantidad de agua le cabría?
b) ¿También la cantidad de agua que se tenía inicialmente se duplicó?
3.- Un tanque de almacenamiento de agua instalado en una comunidad tiene forma de
prisma rectangular y una capacidad de 8 000 litros, su base mide 2.5 m por 2 m.
a) ¿Qué altura tiene este tanque?
b) ¿Qué cantidad de agua contendría si sólo llegara el agua a una altura de 75 cm?
4.- En un envase con forma de prisma cuadrangular cuya base mide 5 cm por lado caben
250 cm3 de aceite.
a) ¿Cuál es la altura de la caja?
b) ¿Cabría la misma cantidad de aceite en un envase forma de pirámide cuya base y
altura sean iguales que en el envase anterior? Justifica tu respuesta.
c) ¿Qué condiciones deben cumplirse para que un envase con forma de prisma y otro
con forma de pirámide que tienen la misma base, tengan la misma capacidad? ¿Por
qué?
Completen la tabla siguiente. Pueden usar calculadora.
Cuerpo
Prisma cuadrangular
Prisma cuadrangular
Prisma cuadrangular
Prisma cuadrangular
Prisma rectangular
Prisma rectangular
Prisma rectangular
Prisma rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del
cuerpo (cm)
Volumen
(cm3)
10
360
360
240
240
160
160
180
180
3
4
9.6
8
5
5
2
2
3
10
20
Hagan una tabla como la anterior y con las mismas dimensiones de la base y altura de los
prismas, calculen el volumen de las pirámides. Pueden usar calculadora.
Cuerpo
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del
cuerpo (cm)
10
3
4
9.6
8
5
5
2
2
3
10
20
Volumen
(cm3)
Si el volumen de las pirámides fuese el mismo que el de los prismas, ¿cuáles deberían ser
las dimensiones? Pueden usar calculadora.
Cuerpo
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del
cuerpo (cm)
Volumen
(cm3)
10
360
360
240
240
160
160
180
180
3
4
9.6
8
5
5
2
2
3
10
20
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1.- En la tienda de Don José se venden 5 kg de naranjas en $16.00. ¿Cuál sería el costo de 9 kg?, ¿y
de 6 kg?, ¿y de un kilogramo?, ¿y de 3 kg? Con los datos anteriores y sus respuestas, completen la
siguiente tabla:
Kilogramos
Costo
¿Qué sucede con el costo al aumentar la cantidad de kilogramos de naranja que se compren?
______________
¿Qué sucede con el costo al disminuir la cantidad de kilogramos de naranja que se compren?
______________
2.- Una empresa elaboradora de alimentos para animales envasan su producción en bolsas de 3kg,
5kg, 10kg, 15 kg y 20 kg. Si dispone de 15 toneladas a granel, ¿cuántas bolsas utilizaría en cada
caso?. Completa la tabla siguiente con los datos que obtuvieron.
Kilogramos
No. Bolsas
¿Qué sucede con el No. de bolsas al aumentar la cantidad de kilogramos en cada una?
______________
¿Qué sucede con el No. de bolsas al disminuir la cantidad de kilogramos en cada una?
______________
¿Qué observan entre el comportamiento de los datos de la primera tabla con respecto a los de la
segunda tabla? ______________________________________________
1. La tabla siguiente muestra el perímetro (P) de un cuadrado de longitud l por lado, para distintos
valores de l. Hacen falta algunos datos complétenla:
l
P
2
16
6
24
8
40
¿Qué tipo de variación observan en esta tabla? ______________
¿Cuál es la constante de proporcionalidad? ______________
¿Cómo determinaron la constante de proporcionalidad? _________________________
2. En la siguiente tabla se muestran algunos valores de la base y la altura de un rectángulo cuya área
es constante. Anoten los datos que faltan.
Base (b)
Altura (h)
2
24
3
8
4
4
¿Cuál es el área del rectángulo? _____________
¿Qué tipo de variación observan en esta tabla? ______________
¿Cuál es la constante de proporcionalidad? ______________
¿Cómo determinaron la constante de proporcionalidad?
___________________________________________
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1. Una persona da 420 pasos de 0.75 m cada uno para recorrer cierta distancia, ¿cuántos
pasos de 0.70 m cada uno necesitaría para recorrer la misma distancia?
2. Un coche tarda 9 horas en recorrer un trayecto siendo su velocidad de 85 km por hora.
¿Cuánto tardará en recorrer el mismo trayecto a 70 km por hora?
3. En una fábrica de chocolates se necesitan 3 600 cajas con capacidad de ½ kg para
envasar su producción diaria. ¿Cuántas cajas con capacidad de ¼ de kg se necesitarán
para envasar la producción de todo un día? ¿Y si se quiere envasar la producción diaria
en cajas cuya capacidad es de 300 g?
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1. En el lanzamiento de una moneda al aire:
a. ¿Qué es más probable, que se obtenga sol o águila? ______________________
b. ¿Cuál es la probabilidad de obtener águila? _____________________¿Cuál es la
probabilidad de obtener sol? ________________________
2. En el lanzamiento de un dado al aire:
a. ¿Qué es más probable, que se obtenga 1 o 4? ___________________________
b. ¿Cuál es la probabilidad de obtener 1? _______________________ ¿Cuál es la
probabilidad de obtener 4? __________________________
c. ¿Cuál es la probabilidad de obtener un número mayor a 4? ________________
d. ¿Cuál es la probabilidad de obtener cualquier número del dado? ____________
3. En el lanzamiento simultáneo de una moneda y un dado al aire:
a. ¿Cuál es la probabilidad de obtener águila y el número 3? _________________
b. ¿Cuál es la probabilidad de obtener sol y un número par? _________________
4. En el lanzamiento simultáneo de dos dados al aire:
a. ¿Cuál es la probabilidad de obtener dos números impares? ________________
b. ¿Cuál es la probabilidad de obtener un número par y uno impar? ____________
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1. El juego de los volados consiste en lanzar una moneda al aire y predecir el resultado
(águila o sol). ¿Cuál es la probabilidad de que caiga águila? ______________ ¿Y de
que caiga sol? ____________________________
2. Ahora lancen 20 veces una moneda y registren sus resultados en la siguiente tabla.
a) ¿Cuántas águilas cayeron? ______________________
b) Escriban el cociente del número de águilas entre el total de volados.
_____________
c) ¿Qué relación observan entre el cociente que escribieron y la probabilidad de caer
águila que obtuvieron sin hacer el volado en la actividad 1? ________________
3. En el pizarrón, con ayuda de su maestro, hagan una tabla para registrar los resultados
de todas las parejas del grupo. Escriban también los resultados en la siguiente tabla.
a) ¿Cuántas águilas cayeron en total? __________________
b) Escriban el cociente del número de águilas entre el total de volados. _________
c) ¿Qué relación observan entre el cociente que obtuvieron en pareja y en el grupo,
respecto a la probabilidad que escribieron en la actividad 1 sin hacer el volado?
_________________________________________________________
d) Si lanzaran la moneda 1 000 veces, ¿cuántas veces creen que se obtenga águila?
________ ¿Por qué? _________________________________________________
CONTESTA CORRECTAMENTE LO QUE SE TE PIDE.
1. La maestra de primero grado de secundaria realizó un concurso de conocimientos por
equipos y dijo que el equipo ganador obtendría de regalo un balón. Después los
miembros de ese equipo deberían elegir la forma de asignar el premio entre ellos.
Ganó el equipo formado por Daniela, Verónica, Lulú, Manuel, Rodrigo y Luis.
Para seleccionar al alumno que se llevará el balón, Daniela propuso que fuera
mediante el lanzamiento de un dado. Cada quien elegiría un número y luego se
lanzaría 60 veces el dado; el alumno que haya seleccionado el número que haya
salido más veces, sería el ganador.
a) ¿Quién tiene más posibilidades de ganar, Rodrigo o Verónica? ____________
¿Por qué? ____________________________________________________
b) ¿Cuál es la probabilidad de que Daniela resulte ganadora? ______________
¿Por qué? ____________________________________________________
2. Ahora realicen el experimento para obtener un posible ganador. Tiren un dado 60
veces y registren sus resultados en la siguiente tabla de frecuencias.
a) De acuerdo con los resultados de su experimento, ¿quién ganaría el balón?
_______________ ¿Cuál es la probabilidad de que Manuel se lleve el balón?
__________________
b) Si el experimento se repitiera 600 veces, ¿a qué valor se aproximaría la
probabilidad frecuencial de que resulte ganador Manuel? _____________________