Guía N 4: TRABAJO, ENERGÍA Y POTENCIA

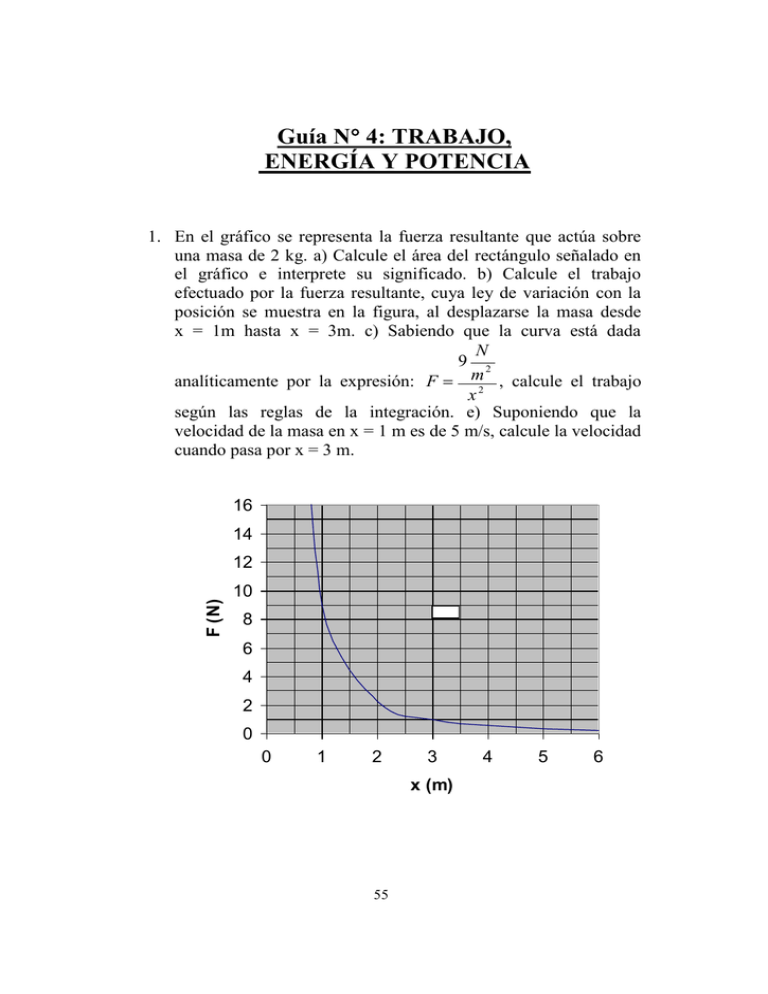
Guía N 4: TRABAJO,
ENERGÍA Y POTENCIA
1. En el gráfico se representa la fuerza resultante que actúa sobre
una masa de 2 kg. a) Calcule el área del rectángulo señalado en
el gráfico e interprete su significado. b) Calcule el trabajo
efectuado por la fuerza resultante, cuya ley de variación con la
posición se muestra en la figura, al desplazarse la masa desde
x = 1m hasta x = 3m. c) Sabiendo que la curva está dada
N
9 2
analíticamente por la expresión: F  m2 , calcule el trabajo
x
según las reglas de la integración. e) Suponiendo que la
velocidad de la masa en x = 1 m es de 5 m/s, calcule la velocidad
cuando pasa por x = 3 m.
16
14
F (N)
12
10
8
6
4
2
0
0
1
2
3
x (m)
55
4
5
6
Respuesta: 6 N . m;
5,57
m
.
s
2. Un resorte tiene una constante de fuerza de 15.0 N/cm. a)
¿Cuánto trabajo se debe realizar sobre el resorte para estirarlo
7.60 mm desde su posición sin deformación? b) ¿Cuánto trabajo
es necesario para estirar el resorte 7.60 mm más?
Respuesta:  4,3.102 J ;  0,13 J .
F (N)
3. Un bloque de 5 kg se mueve en línea recta sobre una superficie
horizontal sin fricción bajo la influencia de una fuerza que varía
con la posición, como se muestra en la figura. a) ¿Cuánto trabajo
efectúa la fuerza cuando el bloque se mueve desde el origen
hasta x = 8.0 m? b) Si la velocidad del bloque en x = 0 es de 8
m/s, ¿cuál será su velocidad en x = 8 m? ¿Y en x = 4 m?
22
20
18
16
14
12
10
8
6
4
2
0
0
2
4
6
8
10
12
x (m)
Respuesta: 113,3 J ; 10,45
m
m
; 9,69 .
s
s
4. Se usa una cuerda para bajar verticalmente un bloque de masa M
a una distancia d con una aceleración constante hacia abajo de
g/4. a) Halle el trabajo efectuado por la cuerda sobre el bloque.
56
b) Halle el trabajo efectuado en el mismo trayecto por la fuerza
de gravedad.
Respuesta:
3
M . g .d ;
4
M .g . d .
5. Una pelota pierde el 15.0% de su energía cinética cuando rebota
en una acera de concreto. ¿A qué velocidad deberá ser arrojada
hacia abajo verticalmente desde una altura de 12.4 m para que
rebote hasta esa misma altura? Desprecie la resistencia del aire.
Respuesta: 6,61
m
.
s
6. Un hombre que corre tiene la mitad de la energía cinética que
tiene un niño. La masa del hombre es el doble que la masa del
niño. Cuando el hombre aumenta su velocidad en 1 m/s tiene la
misma energía cinética que el niño. ¿Cuáles eran las velocidades
originales del hombre y del niño?
m
m
Respuesta: 2,41 ; 4,82 .
s
s
7. Un automóvil de 1110 kg viaja a 46 km/h por una carretera llana.
Se accionan los frenos para disminuir en 51 kJ su energía
cinética. a) ¿Cuál es la velocidad final del automóvil? b) ¿Cuánta
más cantidad de energía cinética deberá eliminarse por los
frenos para detener el automóvil?
Respuesta: 8,45
m
;
s
39,6 kJ .
8. El gráfico siguiente
muestra como varía,
en
función
del
tiempo, el módulo de
la fuerza F resultante
que actúa sobre una
partícula de 20 kg de
masa, inicialmente en
reposo,
que
se
F
100 N
0
57
20
s
t
desplaza sobre el eje x. Obtenga por integración la velocidad de
la partícula a los 10 s y a los 20 s, la energía cinética de la masa
en los mismos instantes y el trabajo que realiza la fuerza entre 0
s y 10 s y entre 10 s y 20 s.
m
;
s
Respuesta: 37,5
50
m
;
s
14 kJ ;
25 kJ ; 14 kJ ;
11 kJ .
9. El
gráfico
siguiente
muestra como varía, en
F
función de la posición, el
módulo de la fuerza F 100 N
resultante que actúa sobre
una partícula de 20 kg de
masa, inicialmente en
reposo, que se desplaza
20 m
0
x
sobre el eje x. Obtenga
por
integración
la
velocidad de la partícula a los 10 m y a los 20 m, la energía
cinética de la masa en las mismas posiciones y el trabajo que
realiza la fuerza entre 0 m y 10 m y entre 10 m y 20 m.
m
;
s
Respuesta: 8,66
10
m
;
s
750 J ;
1 kJ ;
750 J ;
250 J .
10. Un cuerpo de 0,1 kg cae desde una altura de 3 m sobre un
montón de arena, penetrando en ella 5 cm hasta detenerse.
Calcule la fuerza de rozamiento entre el cuerpo y la arena
suponiéndola constante en los 5 cm.
Respuesta: 61N .
11. Un plano inclinado tiene 13 m de largo y 12 m de base. Un
bloque de 0,8 kg resbala hacia abajo sin rozamiento sobre el
plano. Si en el extremo superior tiene una velocidad de 4 m/s,
calcule la velocidad y la energía cinética del bloque en la base
del plano.
Respuesta: 10,8
m
; 46,4 J .
s
58
12. Un cuerpo cae libremente desde una altura h sobre el piso.
Analice cualitativamente cómo cambia su energía cinética y su
energía potencial en función de la altura. Analice también que
ocurre con la energía mecánica.
13. Un automóvil de 1600 kg sube por un camino inclinado 15º con
velocidad constante de 45 km/h. Despreciando los rozamientos
pasivos, haga un balance energético para este problema (esto
significa analizar cómo y por qué varían las energías cinética,
potencial y mecánica del auto) y calcule la potencia que
desarrolla el motor en HP y en kwatt y el trabajo entregado por
el motor en 10 minutos, expresando el resultado en Joule y en
kwatt.h.
Respuesta: 51.76 kWatt ;
69 HP ;
3,1.107 J ;
8,6 kWatt . h .
14. En un teleférico para esquiadores con cabida para 100 personas,
una máquina eleva a los 100 pasajeros, que promedian 667 N de
peso, a una altura de 152 m en 55.0 s, a velocidad constante.
Halle la potencia suministrada por el motor, suponiendo que no
existan pérdidas por fricción.
Respuesta: 1,84.105 Watt .
15. Al comenzar una carrera, un corredor de 68 kg corre los
primeros 7 m en 1.60 s, comenzando desde el reposo y
acelerando uniformemente. a) ¿Cuál es la velocidad del corredor
al final de 1.60 s?, b) ¿Qué potencia promedio genera el corredor
durante el intervalo de 1.60s?
m
Respuesta: 8,75 ; 1627 Watt.
s
16. En una cascada de 96.3 m de altura pasan 73800 m3 de agua por
minuto. Suponiendo que el 58.0 % de la energía cinética ganada
por el agua al caer sea convertida a energía eléctrica por un
generador hidroeléctrico, calcule la potencia de salida del
generador.
Respuesta: 6,87. 108 Watt .
59
17. Demuestre que la velocidad v alcanzada por un automóvil de
masa m que es impulsado con una potencia constante P está dada
1/ 3
3x P
por: v  
 , donde x es la distancia recorrida desde el
 m 
reposo.
18. Demuestre que la potencia desarrollada por un avión que viaja a
velocidad constante v en un vuelo a nivel es proporcional a v3.
Suponga que la fuerza de arrastre está dada por D = b v2. b) ¿En
qué factor deberán aumentar su potencia los motores para
aumentar la velocidad en el aire en 25.0%?
19. Un regulador consta de
dos esferas de 200 g
unidas
por
varillas
rígidas, de 10.0 cm de
longitud, a un eje
vertical giratorio. Las
varillas están acopladas

de modo que las esferas
puedan oscilar desde el
eje al girar con él. Sin
embargo, cuando el
ángulo  es de 45º, las
esferas tocan la pared
del cilindro dentro del
que está girando el
regulador.
a)
¿Cuál es la frecuencia mínima de rotación, en revoluciones por
minuto, necesaria para que las esferas toquen la pared? b) Si el
coeficiente de fricción cinética entre las esferas y la pared es de
0.35, ¿qué potencia se disipa debido a que las esferas frotan
contra la pared cuando el mecanismo está girando a
300
rev/min?.
Respuesta: 112RPM; 18.59 Watt .
20. Un cuerpo de 4 kg se mueve hacia arriba sobre un plano
inclinado 30º, sometido a la acción de una fuerza de 25 N
paralela al plano y en el sentido del movimiento, otra de 80 N en
60
dirección horizontal que también "ayuda" al movimiento, y una
fuerza de fricción de 10 N que se opone a él. Si el cuerpo tiene
una velocidad inicial de 10 m/s y se desplaza 20 m en estas
condiciones, halle su velocidad final. Sugerencia: primero haga
un diagrama de las fuerzas que actúan sobre el cuerpo, vea si
realizan trabajo o no, y finalmente haga el balance energético.
Respuesta: 27,16 m/s.
21. Una partícula desliza por una vía que tiene la forma indicada en
el diagrama. En la parte plana, el coeficiente de rozamiento
dinámico entre el bloque y el piso es 0,2. En las porciones curvas
de la vía la masa desliza con rozamiento despreciable. Si el
movimiento comienza en el punto A, que se encuentra a 1 m de
alto, determine en que punto del plano horizontal quedará
finalmente detenida.
A
1m
B
Respuesta: a 5 m del punto B.
22. Un trineo de 20 kg de masa desliza hacia abajo, partiendo del
reposo, desde una altura de 20 m, adquiriendo al llegar a la base
una velocidad de 16 m/s. Explique las transformaciones de
energía de este sistema. ¿Toda la energía potencial del trineo se
transforma en cinética al llegar a la base? Compárelas y extraiga
conclusiones.
23. Una bola de 5 kg se lanza hacia arriba con velocidad inicial de
20 m/s y alcanza una altura máxima de 15 m. Calcule la pérdida
de energía de la bola debida a la resistencia del aire.
61
Respuesta: 250 J .
24. Un bloque de 1 kg choca contra un resorte ideal cuya constante
de elasticidad es 20 N/m. Sabiendo que la compresión máxima
que experimenta el resorte es 0,4 m, calcule la velocidad del
bloque en el instante de chocar, y la que tenía 3 m antes, primero
suponiendo que el rozamiento con el piso es despreciable y
luego asumiendo que el coeficiente dinámico de fricción entre el
bloque y el piso es de 0,2. En cada caso analice previamente que
ocurre con la energía de este sistema a medida que el bloque se
mueve. Compare ambos resultados, ¿es lo que Ud. esperaba?
Explique.
k
v
Respuesta: 1,79
m
m
, 1,79
;
s
s
2,19
m
,
s
4,1
m
..
s
25. El cuerpo A de la figura
tiene 0,5 kg de masa.
Partiendo del reposo
resbala 3 m sobre el plano
3m
hasta chocar con el resorte
M cuya constante de
elasticidad es 400 N/m.
Explique
las
k
transformaciones
de
energía para este sistema
 = 30
y calcule la máxima
deformación del resorte.
El coeficiente de rozamiento entre el bloque y el plano es 0,2.
Calcule también a qué distancia máxima del extremo libre del
resorte se aleja luego del primer rebote.
62
Respuesta: 0,16 m; 1,52 m.
26. Un cuerpo de 3 kg se deja caer desde una altura de 1 m sobre el
extremo superior de un resorte dispuesto verticalmente sobre el
piso. Si la constante elástica del mismo es de 400 N/m, calcule la
máxima deformación que experimentará. Tenga en cuenta que el
bloque, al quedar nuevamente detenido, recorrerá algo más que 1
m.
Respuesta: 0,47 m .
27. El cable de un ascensor de 1800 kg
se corta cuando el ascensor se halla
en reposo con su fondo a una altura
de 4 m sobre un resorte
amortiguador
cuya
constante
elástica es de 146000 N/m. Si al
movimiento del elevador se opone
una fuerza de rozamiento de 4500
N, halle: a) la velocidad del
ascensor al chocar contra el resorte.
b) la máxima deformación que éste
experimenta. c) la altura sobre el
extremo superior del resorte a la que
se elevará el fondo del ascensor
luego del rebote. d) la distancia total que recorrerá el ascensor
hasta que quedará finalmente detenido.
Respuesta: 7,73
m
;
s
0,96 m ;
2,03m ; 16,24 m .
28. Un cuerpo de 2 kg es empujado hacia arriba sobre un plano
inclinado 30º, de 3 m de longitud, mediante una fuerza
horizontal F. Si la velocidad del bloque en el extremo inferior
del plano es 0,66 m/s y en el extremo superior es 2,8 m/s,
calcule el módulo de la fuerza F y el trabajo que realiza sobre el
cuerpo.
Respuesta: 14,5 N; 37,4 J.
63
29. Un péndulo simple está formado por una masa puntual de 0,4 kg
unida a un hilo de 1,2 m de longitud. Si el péndulo oscila con
una amplitud angular de 90º, calcule la tensión del hilo y la
velocidad de la masa cuando ésta pasa por la posición de
equilibrio. Compare el valor que halló para la tensión con el peso
de la lenteja, ¿le parece lógico? Explique.
m
Respuesta: 12 N ; 4,90 . .
s
30. ¿Qué velocidad debería tener la lenteja del péndulo del problema
anterior al pasar por la posición en la que el hilo queda
horizontal, para que en la posición de equilibrio (hilo vertical) la
tensión de la soga sea 20 N?
Respuesta: 4,90
m
.
s
31. Una vagoneta de 20 kg desciende desde el reposo sobre una vía
inclinada que se empalma con otra en forma de bucle circular de
2 m de radio. Calcule desde que altura mínima debe caer para
que pueda recorrer toda la circunferencia sin apartarse de la vía.
Obtenga para este mismo caso la fuerza normal que ejerce la vía
sobre el carro en el punto M. Calcule desde que altura debería
caer para que la fuerza normal de la vía sobre el carro en el
punto N sea igual a 200 N.
N
M
Respuesta: 5 m ; 600 N ; 6 m .
64
32. Una masa puntual
comienza a caer,
partiendo
del
reposo, desde el
punto superior de
una
superficie
R
esférica de radio R.

Obtenga,
por
consideraciones
energéticas,
la
energía cinética, la velocidad de la partícula y la reacción
normal de la superficie sobre ella en función del ángulo . A
partir de esta última expresión calcule para qué valor de  la
masa pierde contacto con la superficie.
Respuesta:
E c  m . g . R 1  cos ;
N  m . g 3 . cos  2 ;
v  2 . g . R 1  cos  ;
480
.
33. En cada uno de los siguientes sistemas estudie las
transformaciones de energía que se producen cuando el bloque
de masa m1 desciende 1 m a partir del reposo. Analice si cada
uno de los bloques conserva o no su energía mecánica. ¿Y el
sistema formado por ambos bloques es conservativo? Explique.
m1 = 10 kg, m2 = 8 kg
m2
a
m2
b
m1
m1
65
34. Una gran central nuclear produce 3000 MW de potencia por
fisión nuclear, que convierte la masa m en energía según la
fórmula de Einstein: E = m.c2, donde c es la velocidad de la luz
en el vacío. a) ¿Cuánta masa se convierte en energía al cabo de
un año? b) En una central térmica de carbón, cada kilogramo de
carbón libera en la combustión 31 MJ de energía. ¿Cuántos
kilogramos de carbón se necesitarán anualmente para una central
térmica de 3000 MW?
35. Se cree que el sol obtiene su energía por un proceso de fusión en
el cual cuatro átomos de hidrógeno se transforman en un átomo
de helio con emisión de energía en diversas formas de radiación.
Si las masas en reposo de los átomos de hidrógeno y helio son
respectivamente 1,0081 uma y 4,0039 uma, calcule la energía
desprendida en cada proceso de fusión. (Una unidad de masa
-27
atómica equivale a 1,67.10 kg)
36. Se empuja hacia una lado la lenteja de un péndulo de longitud L
de modo que la cuerda forme un ángulo 0 con la vertical, y
luego se lo suelta. En otros problemas de esta guía Ud. utilizó el
principio de conservación de la energía para obtener la velocidad
de la lenteja al pasar por la posición más baja de la trayectoria.
En este problema se pide resolver lo mismo pero por aplicación
de la segunda ley de Newton. a) Demuestre que la componente
dv
tangencial de la aceleración es a 
 g. sin donde v es la
dt
velocidad y  es el ángulo que forma la cuerda con la vertical. b)
d
Demuestre que v se puede escribir como: v  L
. c) Utilice
dt
este resultado y la regla de derivación en cadena para obtener:
dv dv d dv v
. d) Combine los resultados de a) y c) para


dt d dt d L
obtener v. dv   g. l. sin  . d . e) Integre ahora el primer
miembro de esta ecuación desde v = 0 hasta la velocidad final v
y el segundo miembro desde  = 0 hasta  = 0 y demuestre que
el resultado es equivalente a: v  2. g. h , siendo h la altura
original de la lenteja del péndulo sobre la posición más baja del
trayecto.
66