http://mundogenial.com/archivos/RAZONAMIENTO%20ARITM%c3%89TICO%201%20-%202015.pdf

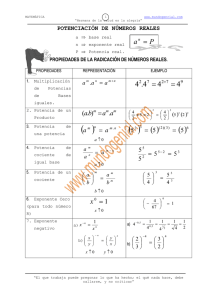
RAZONAMIENTO
1
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
1)
Multiplicar los siguientes productos:
2)
( 1 ) x ( 91 ) =
( 2 ) x ( 91 ) =
¡El curioso número 37!
Halla el valor de las
multiplicaciones
( 3 ) x( 37 ) =
( 3 ) x ( 91 ) =
( 6 ) x( 37 ) =
( 4 ) x ( 91 ) =
( 9 ) x( 37 ) =
( 5 ) x ( 91 ) =
( 12 ) x( 37 ) =
( 6 ) x ( 91 ) =
( 15 ) x( 37 ) =
( 7 ) x ( 91 ) =
( 18 ) x( 37 ) =
( 8 ) x ( 91 ) =
( 21 ) x( 37 ) =
( 9 ) x ( 91 ) =
( 24 ) x( 37 ) =
( 27 ) x( 37 ) =
3)
4)
Calcular y descubra la propiedad correspondiente:

332 

3333332 

3332 

33333332 

33332 

333333332 

333332 

3333333332 
Calcular y descubra la propiedad correspondiente:

66 2 

666666 2 

666 2 

6666666 2 

6666 2 

66666666 2 

66666 2 

666666666 2 
siguientes
RAZONAMIENTO
2
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
5)
6)
7)
8)
Calcular y descubra la propiedad correspondiente:

682 

6666682 

6682 

66666682 

66682 

666666682 

666682 

6666666682 
Calcular y descubra la propiedad correspondiente:

952 

9999952 

9952 

99999952 

99952 

999999952 

999952 

9999999952 
Calcular y descubra la propiedad correspondiente:

92 

999992 

992 

9999992 

9992 

99999992 

99992 

999999992 
Calcula la suma de cifras de:
A  (11111...1113) 2  (1111...11111) 2
 
100 cifras
9)
100 cifras
a) 504
b) 404
c) 234
Calcular la suma de cifras de:
N  (323232
3232
...

 ).6
d) 202
e) 909
a) 3633
d) 3424
e) 3604
604 cifras
b) 3624
c) 3618
RAZONAMIENTO
3
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
10) Calcular el valor B y dar como respuesta la suma de sus cifras: B  (666666666666) 2
a) 102
b) 140 c) 108 d) 110 e) 111
11) Calcular la suma de cifras del resultado:
C  (555...555) x (999...999)
 
100 cifras
100 cifras
a) 1
b) 10
c) 100
d) 90
2
2
12) Si: A  (3333...3333) y A  (666...6666)





61cifras
e) 900
31cifras
Calcular la diferencia entre la suma de cifras del resultado de A y la suma de cifras del
resultado de B.
a) 720
b) 270
c) 828
d) 279
e) 549
13) Calcular la suma de cifras del resultado de “B”
A  (999...9995) 2



101cifras
a) 90
b) 925 c) 625 d) 900 e) 907
14) Calcular la suma de cifras del resultado de efectuar: E  81(12345679) 2
a) 49
b) 100 c) 72 d) 81 e) 64
15) Calcular l suma de cifras del resultado de:
2
2
E  (5555
...
556
...
445

 )  (4444

)
101 cifras
101cifras
a) 203
b) 205
c) 206
d) 202
e) 102
16) Hallar “P”, si hay cantidad de números negativos y positivos.
P  ...
 3
1
 2

4 6

...
5
400 cifras
a) 100
b) 200
c) 150
d) 250
e) 280
17) Indicar la suma de las cifras del resultado al efectuar la expresión siguiente:
A  (666...6666) 2



666 cifras
a) 1998
b) 1332
c) 6998
d) 5994
e) 1292
18) Calcular: 366  463  251  234  137  366  234  349 
a) 137
b) 401
c) 300
d) 600
e) 400
19) Calcular: 20032003 2  20032002 2  . E indicar la suma de cifras del resultado.
a) 7
b) 11
c) 19
d) 17
e) 8
RAZONAMIENTO
4
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
20) Calcular: 9995 2  9994 2  . E indicar la suma de cifras del resultado.
a) 37
b) 38
c) 39
d) 47
e) 48
21) ¿Cuál de las siguientes expresiones es menor que 5?
5
5
a)
5 
5
5
5 x5
b) 5 
5
5
5(5 x5)
c)
55
555

d)
55
5 x5 x5

e)
5 x5
22) Calcular la suma de cifras del resultado de E:
E  (1).(3).(5).(17).(257)  1
a) 16
b) 12 c) 13
d) 10
e) 6
23) Calcular la suma de cifras del resultado de efectuar: M  (777778) 2  ( 222223) 2
a) 20
b) 30
c) 35
d) 42
e) 43
24) Encuentra el resultado de las siguientes potencias:
12
=
112
=
1112
=
11112
=
111112
=
1111112
=
11111112
=
111111112
=
1111111112
=
RAZONAMIENTO
5
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
(Esta curiosidad se cumple solamente hasta el caso en que la base tenga 9 cifras uno)
25) Hallar la suma de cifras del resultado de: 1111111112 =
a) 9
b) 18
c) 90
d) 1
e) 81
26) A continuación te presentamos una tabla de doble entrada en la cual cada elemento de la
naturaleza representa un número de una cifra y que sumados ya sea de forma horizontal
o vertical dan como resultado los valores que se consignan.
Es obvio que el mismo dibujo representa siempre el mismo número.
14
15
16
17
18
19
37
9
23
30
27) ¡VAYA MULTIPLICACIONES¡: Observa cuidadosamente estas operaciones
Podrías indicar sin necesidad de utilizar calculadora, ni multiplicar, cuales son los valores
de las variables en las siguientes operaciones:

(1).(2).(3).(4)  1  25  5 2

(2).(3).(4).(5)  1  121  112

(3).(4).(5).(6)  1  361  19 2
RAZONAMIENTO
6
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”

(4).(5).(6).(7)  1  ............  a 2

(5).(6).(7).(8)  1  ............  b 2

(6).(7).(8).(9)  1  ............  c 2

(7).(8).(9).(10)  1  ............  d 2

(8).(9).(10).(11)  1  .............  e 2

(9).(10).(11).(12)  1  .............  e 2
28) Como sabemos el número dos es un número muy especial, por ejemplo es el único
número primo par, está presente en la fórmula para el cálculo del área de un triángulo y
en el cálculo de las áreas de otras figuras geométricas.
Recurre a tu habilidad operativa para que con cinco veces el número 2, y utilizando sólo
las cuatro operaciones fundamentales: +; -; x; /, y los necesarios signos de colección,
escribas los números desde el 0 hasta el 10.
0
5
1
6
2
( 22  2 )  ( 2 ).( 2 )
7
3
8
4
9
 10
29) Halla el resultado de:
PIRÁMIDE NUMÉRICO
1X9 + 2 =
12X9 + 3 =
123X9 + 4 =
1234X9 + 5 =
12345X9 + 6 =
123456X9 + 7 =
1234567X9 + 8 =
12345678X9 + 9 =
RAZONAMIENTO
7
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
30) Calcular la suma de cifras del resultado de:



...
11100
A  (444...448) 2  (444...447) 2  111
   
 
100
cifras
100 cifras
 100 cifras

a) 898
b) 916
c) 891
2
d) 716
e) 457
31) Hallar la suma de cifras del producto:
B  (7777
...
777
99)

 ).(9999
...

1275 cifras
1275 cifras
a) 11 895
b) 11 475
c) 12 891
32) Hallar la suma de cifras del resultado de:
a) 8
b) 9
d) 15715
e) 455
P  123456789  2468
c) 11
d) 111
e) 5
33) Hallar la suma de cifras de:
A  (7777
...
777
99)

 ).(9999
...

50 cifras
50 cifras
a) 320
b) 480 c) 360
d) 510
34) Calcular la suma de cifras del resultado:
M  (12345678) 2  (12345676 ) 2
a) 32
b) 48
c) 36
e) 450
d) 41
e) 45
35) Calcular la suma de cifras del resultado:
M  (99).(100).(101).(102)  1
a) 20
b) 19 c) 12
d) 25
e) 15
36) Calcular la suma de cifras del resultado:
(135) 2  85  65  145
2
a) 20
2
2
b) 19 c) 12
d) 25
e) 15
37) ¿Qué número continúa? 8; 16; 17; 34; 35; 70; ………
a) 80
b) 71 c) 72
d) 85
e) 75
38) Calcular la suma de cifras del resultado de:
 __________________________________________
__________________________________________ 
A  (a  3)(a  3)...(a  3)(a  3)(a  3)  (a  3)(a  3)...(a  3)(a  3)(a  3)

 

 
101 cifras
101cifras


a) 680
b) 671
c) 610
d) 810
e) 775
2
RAZONAMIENTO
8
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
39) Si:
d
______
abcd  d , calcular: R 
a) 8
b) 7
c) 2
(a).(b)  d
c
d) 4
e) 5
_____
40) Hallar la suma de cifras del resultado de multiplicar " (abc).(512)" , sabiendo que la suma
de los productos parciales de esta multiplicación resulta 3496.
a) 22
b) 41
c) 32 d)
15
e) 7
41) Si: a, b y c  Z  y se cumple que:
a + b + c = 11
a 2  b 2  c 2  49
Calcular: D  (a  b) 2  (b  c) 2  (c  a) 2
a) 180
b) 171
c) 178
d) 170
e) 270
42) Halla el valor de: D  (7000) 3  (6999) 3  (6999) 2  7(6999 )(10) 2
a) 1800
b) 7000
c) 6999
d) 17000
e) 2700
43) PROBLEMA RECREATIVO: Mover un dígito y hacer que la igualdad sea correcta :
44) PROBLEMA RECREATIVO: Moviendo las 4 cifras que aparecen en esta falsa
igualdad, consigue una igualdad verdadera.
45) además: En lugar de ir por los lados de una terreno de 60 por 80 m, para ir de una
esquina a otra, una persona lo atraviesa por su diagonal. ¿Cuántos metros se ahorró?
a) 160 m
b) 40 m
c) 100 m
d) 140 m
e) 60 m
46) La longitud de la sombra de un árbol es igual a la altura del árbol. ¿Qué ángulo
determinan los rayos solares con la superficie?
a) 300 b) 600
c) 150 d) 450
e) 750
47) Coloca nueve monedas, en cuatro vasos, de tal manera que en cada uno haya un número
impar de monedas.
48) Se han de repartir 160 caramelos entre 45 niños de un salón, dándole 3 caramelos a cada
varón y 4 a cada niña. ¿cuántas niñas hay en esta aula
a) 20
b) 21
c) 225
e) 30
49) Al multiplicar por 73 un cierto número, éste aumenta en 26 280. ¿Cuál es el número?
a) 365
b) 456
c) 456
d) 340
e) 265
50) De la casa a la fábrica gasto S/. 45 y de regreso gasto S/. 90. Si tengo gastado S/. 1 575;
¿dónde estoy?
RAZONAMIENTO
9
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
a) ………………..
51) Multiplicar los siguientes productos:
( 1 ) x ( 91 ) =
( 5 ) x ( 91 ) =
( 2 ) x ( 91 ) =
( 6 ) x ( 91 ) =
( 3 ) x ( 91 ) =
( 7 ) x ( 91 ) =
( 4 ) x ( 91 ) =
( 8 ) x ( 91 ) =
( 9 ) x ( 91 ) =
52) La caída del huevo sin romperse.- Si estamos de pie sobre un piso de mármol, ¿cómo nos
las arreglaremos para soltar un huevo de gallina y hacer que éste recorra en su caída un
metro sin romperse?. No vale colocar ninguna almohada ni cosas blandas para
amortiguar el golpe contra el mármol
……………………………………………………………………………………………………………………………………
……………………………………………………
53) Una persona de 2 metros de estatura observa la parte más alta de una torre con un
ángulo de elevación de 300. ¿A que distancia se encuentran de la base de la torre, si esta
mide 82 m?
a) 80 3 m
b) 80 m
c) 40 m
d) 17 80 m
54) Un niño de 1,5 m de estatura divisa una piedra en el suelo con un ángulo de depresión de
370, ¿a qué distancia del niño se encuentra la piedra?
a) 1 m
b) 2 m
c) 3 m
d) 2,5 m
e) 4 m
55) Un estudiante observa una estatua, con visuales que miden 8 m y 7 m; las cuales forman
un ángulo de 600. Calcule la altura de la estatura.
f) 8 m
g) 2 10 m
h) 65 m
i)
57 m
j) 2 17 m
56) En un Instituto de idiomas, en el que solo se enseña, inglés, francés y ruso, el 70% del
alumnado estudia inglés, el 30% estudia francés, el 10% estudia ruso y ningún alumno
estudia los tres idiomas. ¿Qué porcentaje de los alumnos estudia exactamente un idioma?
a) 50%
b) 60%
c) 70%
d) 80%
e) 90%
RAZONAMIENTO
10
JRC
“El que trabaja puede pregonar lo que ha hecho; el qué nada hace, debe callarse, y no criticar”
57) EL NÚMERO QUE MAS QUIERES: Pídele a un amigo, que escriba todas las cifras del 1 al
9, menos el 8 (1; 2; 3; 4; 5; 6; 7; 9)
Pregúntele cual es la cifra que más desea escribir; el dirá cualquiera (del 1 al 9).
Supongo que dijo el 5.
Pídale que multiplique que el número 12345679 por 45 y el resultado de la operación
estarán compuestos por números iguales, precisamente de la cifra que más desea
escribir, el 5.