IDEA INTUITIVA DE LÍMITE DE UNA FUNCIÓN

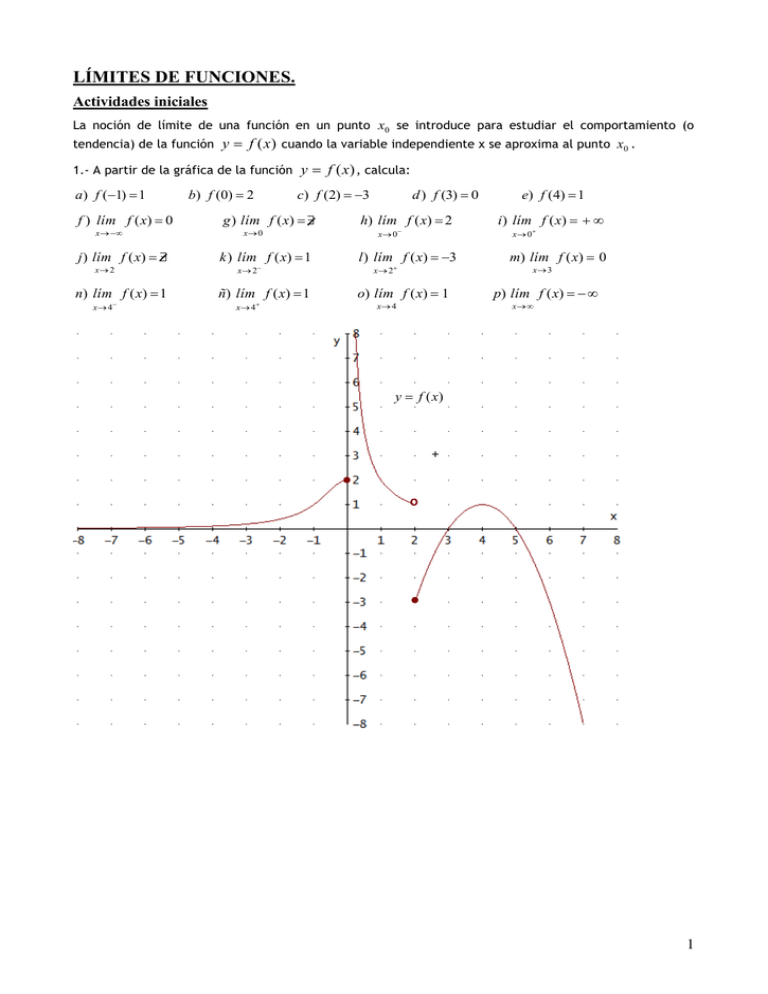
LÍMITES DE FUNCIONES.
Actividades iniciales
La noción de límite de una función en un punto x0 se introduce para estudiar el comportamiento (o
tendencia) de la función y  f (x) cuando la variable independiente x se aproxima al punto x0 .
1.- A partir de la gráfica de la función y  f (x) , calcula:
a) f (1)  1
f ) lím f ( x)  0
x  
j ) lím f ( x)  
x 2
n) lím f ( x)  1
x 4
b) f (0)  2
c) f (2)  3
g ) lím f ( x)  
d ) f (3)  0
h) lím f ( x)  2
x 0
x 0
k ) lím f ( x)  1
l ) lím f ( x)  3
x 2
x 2
ñ) lím f ( x)  1
i) lím f ( x)   
x 0
m) lím f ( x)  0
x 3
o) lím f ( x)  1
x 4
e) f (4)  1
x 4
p) lím f ( x)   
x 
y  f (x)
.
o
.
1
2

 x
2.- Dada la función f ( x)  
 x 1
 x 2  2
si x  1
si  1  x  2
si x  2
Calcula:
a) lím f ( x) 
x  1
Como en x  1 cambia la expresión analítica de la función, tenemos que estudiar los límites laterales.
lím f ( x)  lím

x  1

2  2
x  1
Como lím
x  1
y
lím f ( x)  lím

x  1

x  1
x
1
1 1



x 1 11  2 2
f ( x)  lím f ( x)   lím f ( x) (el límite no existe)
x  1
x  1
b) lím f ( x)
x 2
Como en x  2 cambia la expresión analítica de la función, tenemos que estudiar los límites laterales.
lím f ( x)  lím
x 2

x 2

x
2

2 y
x 1 2 1
Como lím f ( x)  lím f ( x)
x 2
x 2


lím f ( x)  lím x 2  2  2 2  2  2
x 2
x 2
  lím f ( x)  2
x 2
2
.- Concepto de límite de una función en un punto.
Sea f : A  R  R y sea
x0 un punto de acumulación de A.
Diremos que el nº real L es el límite de la función
f cuando x "tiende a" x0 , y escribiremos
Lím f ( x)  L si y solo si   0    0 / x  x0   y x  A  f ( x)  L  
x  x0
Otra definición alternativa: (Utilizando entornos; es la que vamos a adoptar este año).
Lím f ( x)  L si y solo si  E(L ,  )  E( x0 ,  ) /  x  E * ( x0 ,  )  A  f ( x)  E(L ,  )
x  x0
Explicación: Cuando nos aproximamos a
x0 en una cantidad menor que  , entonces el valor que toma la
función en ese punto x , f ( x) , se aproxima al valor del límite, L, en una cantidad menor que
.
Nota aclarativa:
E ( L ,  )  ( L   , L   )  se lee: “entorno de centro L y radio  (epsilon)”.
E( x0 ,  )  ( x0   , x0   )  se lee: “entorno de centro x0 y radio  (delta)”.
E * ( x0 ,  )  E( x0 ,  )  x0   se lee: “entorno reducido de centro x0 y radio  ”.
.- Límites laterales:
La noción de límite lateral aparece cuando nos aproximamos al punto de abscisas
por la izquierda.
x  x0 por la derecha o
Límite lateral por la izquierda:
Lím f ( x)  L si y solo si  E(L ,  )  E  ( x0 ,  ) /  x  E  ( x0 ,  )  A  f ( x)  E(L ,  )
x  x0
x0 , por la izquierda, en una cantidad menor que  , entonces el
valor que toma la función en ese punto x , f ( x) , se aproxima al valor del límite, L, en una cantidad
Explicación: Cuando nos aproximamos a
menor que
.
Límite lateral por la derecha:
Lím f ( x)  L si y solo si  E(L ,  )  E  ( x0 ,  ) /  x  E  ( x0 ,  )  A  f ( x)  E(L ,  )
x  x0
x0 , por la derecha, en una cantidad menor que  , entonces el
valor que toma la función en ese punto x , f ( x) , se aproxima al valor del límite, L, en una cantidad
Explicación: Cuando nos aproximamos a
menor que
.
Nota aclarativa:
E  ( x0 ,  )  ( x0   , x0 )
E  ( x0 ,  )  ( x0 , x0   )
.- Unicidad del límite:
El límite de una función en un punto, si existe, es único.
Si existe el Lím f ( x)  L , entonces este límite es único.
x  x0
En virtud de la propiedad anterior, enunciamos el siguiente resultado:
Lím f ( x)  L si y solo si Lím f ( x)  L  Lím f ( x)
x  x0
x  x0
x  x0
3
Límites infinitos:
Sea f : A  R  R y sea
x0 un punto de acumulación de A.
Lím f ( x)   si y solo si  k  R  E( x0 ,  ) /  x  E * ( x0 ,  )  A  f ( x)  k
x  x0
Ejemplos:
Lím f ( x)  
x 2
Lím f ( x)  
x 3
Límites finitos en el infinito:
Sea f : A  R  R
Lím f ( x)  L si y solo si  E(L ,  )  k  R /  x  k  f ( x)  E(L ,  )
x  
Ejemplos.
Lím f ( x)  0
Lím f ( x)  2
Lím f ( x)  0
Lím f ( x)  2
x  
x  
x  
x  
4
Límites infinitos en el infinito:
Sea f : A  R  R
Lím f (x)   si y solo si  k  R  M  R /  x  M  f ( x)  K
x  
Ejemplos:
Lím f ( x)  
Lím f ( x)  
Lím f ( x)  
Lím f ( x)  
Lím f ( x)  
Lím f ( x)  
x  
x  
x  
x  
x  
x  
5
OPERACIONES CON LÍMITES DE FUNCIONES.
Sea
x0  R donde R  R   ,
Sean f , g : A  R  R dos funciones con Lím f ( x)  L
x  x0
y
Lím g ( x)  L'
x  x0
Se definen las siguientes operaciones con límites:
a) Lím  f  g x   Lím f ( x)  Lím g ( x)  L  L'
x  x0
x  x0
x  x0
b) Lím  k  f  ( x)  k  Lím f ( x)  k  L
x  x0
k  R
x  x0
c) Lím  f  g  ( x)  Lím f ( x)  Lím g ( x)  L  L'
x  x0
x  x0
x  x0
Lím f ( x)
f 
L
x  x0
d ) Lím   ( x) 

x  x0 g
Lím g ( x) L'
 
x x
0


f ) Lím
f ( x) 
e) Lím f ( x) g ( x )   Lím f ( x) 
x  x0
 x x0

x  x0
Lím g ( x )
x  x0
 LL '
Lím f ( x)  L
x  x0
g ) Lím Log a f ( x)  Log a  Lím f ( x)  Log a L
 x  x0

x  x0
Todos estos límites estarán definidos, salvo en los siguientes casos de indeterminación.
 0
;
; 0     ;     ; 1 ;  0 ; 0 0
 0
Si al calcular un límite nos aparece una de estas indeterminaciones, debemos transformar el límite en otro
equivalente (mediante técnicas algebraicas o utilizando la definición del número e) para así, resolver la
indeterminación.
Observación:
No son indeterminaciones los siguientes casos:
  
0  0
k
   en este caso, debemos estudiar los límites laterales.
0
6
.- Situaciones del tipo
K
con K  0
0
Este tipo de situaciones pueden aparecer al estudiar el límite del cociente de dos funciones polinómicas.
En este tipo de situaciones siempre nos encontraremos con dos ramas infinitas: una puede tender a   y
la otra a   , o bien las dos tender a   ó   .
Este tipo de límites está, por tanto, caracterizado por la presencia de una asíntota vertical.
Se resuelven estudiando los límites laterales.
Los límites laterales siempre van a ser   ó  
Si los límites laterales coinciden el límite existe y será   ó   , y si un límite lateral es   y el otro
  , entonces el límite no existe.
Ejemplos:
a) Lím
x 0
K
0
1

x
Estudiamos los límites laterales.
Lím
1 1

 
x 0
Lím
1
1
   
x 0
x 0
x 0
Como Lím
x 0
1
1
1
 Lím se concluye que no existe el Lím
x 0 x
x x 0 x

Nota: Cuando me acerco a 0 por la izquierda ( x  0 ) x toma valores muy cercanos a 0, pero negativos.
En la expresión
1

, 0 es una cantidad muy cercana a cero pero negativa (-0,0000....01)

0

Cuando me acerco a 0 por la derecha ( x  0 ) x toma valores muy cercanos a 0, pero positivos.
En la expresión
b) Lím
x 1
2

x 1
1
, 0  es una cantidad muy cercana a cero pero positiva (0,0000....01)
0
K
0
Estudiamos los límites laterales.
Lím
2 2

 
x  1 0
Lím
2 2

 
x  1 0
x 1
x 1
Como Lím
x 1
2
2
2
 Lím
se concluye que no existe el Lím
x 1 x  1
x  1 x 1 x  1


Nota: 0 es una cantidad muy pequeña pero negativa, por eso -2 partido de 0 es positivo (menos entre
menos es más) y el resultado es   .
Igual explicación se puede dar para el otro límite lateral.
7
c) Lím
x 2
x

x2
K
0
Estudiamos los límites laterales.
Lím
x
2
   
x2 0
Lím 
x
2
   
x2 0
x 2
x 2
Como
x
x
x
 Lím 
se concluye que no existe el Lím
x 2 x  2
x  2 x 2 x  2
Lím 
x 2
d ) Lím
x 0
K
0
3

x2
Estudiamos los límites laterales.
Lím
3
3
   
2
x
0
Lím
3
3
   
2
x
0
x 0
x 0
Como Lím
x 0
e) Lím
x  1
3
3
3
 Lím 2 se concluye que el Lím 2  
2
x 0 x
x 0 x
x
1
x  1
2
K
0

Estudiamos los límites laterales.
Lím
x  1
Lím
x  1
1
x  1
2
1
x  1
Como Lím
x  1
2

1
 
0

1
 
0
1
x  1
2
 Lím
x  1
1
x  1
2
se concluye que el Lím
x  1
1
x  12
 
8
RESOLUCIÓN DE INDETERMINACIONES:
Hacemos un breve repaso del cálculo de límites y resolución de indeterminaciones ya tratados el curso
anterior.
Veamos algunos ejemplos:
. Indeterminaciones del tipo


Calcula los siguientes límites:
a) Lím
x 3  3x 2  4 x  5
2 x 2  3x  1
x 
b) Lím
x 
c) Lím
x 
d ) Lím
x 
e) Lím
x  
4 x3  5 x2  2 x  3
2
x 
x 
x3  x2  3 x  4
x  2 x  2 x  4x  3
4
3
4 x3
 Lím
3 x  4 x  5x  4
3
2
3x
3
2
2
2 x 3  5x  4
x6  x4  2 x3  x2
 Lím
x 
x6  2 x3
4
3
 Lím
x 
x  
 2 x3
x3  2 x3
x6  2 x3
 Lím
3 x2
x x
4
 Lím
x 
 2 x3
x 
2
k
 0 con k  R

Nota :
 Lím
x 
3 x2
x x
2
2
 Lím
x 
2  x 
3 x2
2x
3
2 x3
 Lím
. Indeterminaciones del tipo

x3
1
 Lím  0
4
x  x
x  x
x  3x  4 x  x  5 x  3
4
3
 Lím
3 x2  4 x  5
 2 x3
 Lím
x3
 x
 Lím     
x  2 x 2
x   2 
 Lím
 x3
 x 6
 2  x 
3
 Lím
x 
2

3
2
 2 x3
x6  2 x3

2
0
.
0
Calcula los siguientes límites:
x3  1

x 1 x  1
0
0
a) Lím
1
1
1
 Lím
x 1
0
0
-1
1
1
1
1
1
0
x  1  x 2  x  1  Lím x 2  x  1  12  1  1  3
x 1
0
0
x 1








x  2  x 2  2 x  3  Lím x 2  2 x  3  5  1
x  7x  6

Lím
x 2 x 3  2 x 2  5 x  6
x   2 x  2  x 2  4 x  3
x 2 x 2  4 x  3
15 3
3
b) Lím
1
-2
1
0
-7
-6
-2
4
6
-2
-3
0
1
-2
1
-2
-5
6
-2
8
-6
-4
3
0
9
0
0

0
0


0
0

x  1  x 2  3x  2  Lím x 2  3x  2  Lím x  1  x  2 
x 3  4 x 2  5x  2

Lím
x  1 x 3  x 2  x  1
x  1
x  1
x  1  x  1   x  1
x  1  x 2  1
x2 1
x  2  1
 Lím
x  1  x  1
2
c) Lím
1
-1
1
-1
4
5
2
-1
-3 -2
3
2
1
-1
0
1


1
-1
-1
-1
0
1
0
-1
0


-1 -2
1
2
0
0
 x  2  2 0


x24
x2
  Lím  x  2  2  x  2  2   Lím
d ) Lím 
 Lím



x 2 
x  2 ( x  2) 
x  2  2  x 2 ( x  2)  x  2  2
x22
 x  2  x 2  x  2
1
1
 Lím

x 2
x22 4






Nota: El producto de una suma por una diferencia es una diferencia de cuadrados, es decir, es igual al
cuadrado del primero menos el cuadrado del segundo.
a  b  a  b  a 2  b 2


x2 2 
e) Lím
x 0
 
x22 
x2

2
 22  x  2  4
0
0





x
1  1  x 
x  1 1 x
x  1 1 x
 Lím 

 Lím
 Lím

2


x

0
x

0
x

0
2


1

1

x
1 1 x
1

1

x
1

1

x


1  1 x
x








x  1 1 x
x  1 1 x
 Lím
 Lím 1  1  x  2
x 0
x 0
x 0
11 x
x
 Lím
0
f ) Lím
x 1
 Lím
x 1
 Lím
x 1

 3x  2  4x 3 3x  2  4x 3 
3x  2  4x 3 0

 Lím 


x 1 
x 1
x

1
3
x

2

4
x

3


3x  2
x  1  
x  1  
 
2
4x3

2
3x  2  4x 3
 x 1
3x  2  4x 3

 Lím

 Lím
x 1
x 1
3 x  2  4 x  3
x  1  
x  1  
3x  2  4x 3
 x  1
3x  2  4x 3

 Lím

 Lím
x 1
3x  2  4 x  3
x  1  
x 1

3x  2  4x 3
1
3x  2  4x 3



1 1

11 2
10
0
0
  x  2  2   2 x  2 
 2 x  2   2 x  2   x  2  2
 x  2   2    2 x  2 


x  2  4   2 x  2  Lím x  2   2 x  2  2  2  2 
 Lím 
 Lím
 2 x   2    x  2  2 
2 x  4   x  2  2
2  x  2   x  2  2 2   2  2  2


g ) Lím
 x  2  2 x  2  2 2x  2 
  Lím
 Lím 


x 2 
2x  2
x  2  2 2 x  2  x 2
 2x  2
x2 2
x 2
2
x 2

2

42


x2 2 
2
2
42

x 2
2
x 2
22
4 1
 
2  2  2 8 2
. Indeterminaciones del tipo 0  
Este tipo de indeterminaciones se resuelven transformándolas en las del tipo
0

ó en las del tipo .
0

Calcula el siguiente límite:
1

Lím   x 2  3 x  
x   x

 x 2  3x 

 Lím 

x  
x


0


 x2 
  Lím x  1
 Lím 
x   x 
x  x


. Indeterminaciones del tipo   
Calcula los siguientes límites:
a) Lím  4 x  5 x  2 x  
x  

2
 Lím
x 
 Lím
x 
4 x2  5 x  4 x2
4 x 2  5 x  2x

5x
 Lím
x 
4 x 2  5 x  2x



5x
 Lím
x 
4 x 2  2x
 Lím
x 
5x

2x  2x
5x 5

4x
4
 x2  2 x2  1

b) Lím 


x 
x

1
x


 Lím
 4 x 2  5 x  2 x    4 x 2  5 x  2 x 
 

 Lím 
x 
2
 4 x  5 x  2 x 




 Lím
  Lím x
x3  2 x  x3  x2  x  1
x 
x x
2
x 
x 
3




x  x 2  2  x  1  x 2  1

x  x  1
 2 x  x3  x2  x  1
x x
2
 x2  x 1

x 
x2  x
 Lím


 x2
 1
x  x 2
 Lím
11
. Indeterminaciones del tipo 1
x

x   
Se resuelven aplicando la definición del nº e: Lím 1 
1
  e , o bien, aplicando directamente la
x
siguiente fórmula:
Lím  f ( x)
e
g ( x)
x  x0
Lím
x xo
 g ( x )   f ( x) 1 
donde x0  R   
Veamos algunos ejemplos:
 x2 

a) Lím  2
x  x  3 


x2
1



x2
 Lím 1  2
 1
x 
x 3 

x2
(sumamos y restamos "1" en la base)

x2  x2  3 

 Lím 1 
x 
x 2  3 

x2
3 

 Lím 1  2

x   
x  3
x2

(dividimos el numerador y el denominador entre (-3))

3 


 Lím 1  2 3 
x   
x 3


3 

x2




1 
 Lím 1  2
x   
x 3


3 

x2

(el siguiente paso es conseguir la misma expresión en el exponente y en el denominador de la base)
x 2  3 3
x 

 3 x 2  3
2



1 
 Lím 1  2
x   
x 3


3 





1 
 Lím 1  2
x  
x 3




3 

x 2 3
 3







x2 
3
x 2 3
3 x 2




1 
 Lím 1  2
x  
x 3




3 

x 2 3
 3
 x 2 3







(aplicamos la definición de número e)
e
Lím
x 
 3 x 2 


 x 2 3 


e
Lím
x 
 3 x 2

 x2





1
e3
 e 3 
Vamos a resolver este mismo límite aplicando la fórmula:
Lím  f ( x)
e
g ( x)
x  x0
 x2 

a) Lím  2
x  x  3 


Lím
e
x 
 3 x 2 


 x 2 3 


x2

Lím
x 
e

1
 3 x 2

 x2





Lím
x xo
e
 g ( x )   f ( x) 1 
Lím
x 
 e 3 
2


 2  x

 x   2 1  
x

3


 

e
Lím
x 
2
2

 2  x  x 3  

x 

2
x

3  

 

e
Lím
x 
 2  3  
 x  2 
  x 3  

1
e3
Como vemos resulta mucho más fácil aplicar la fórmula para calcular el límite (así lo haremos de ahora en
adelante)
2
x
b) Lím 1  3 x  
x 0
1
e
2

Lím  13 x 1
x 0  x

e
Lím
x 0
6x
x
 e6
12