R I V 

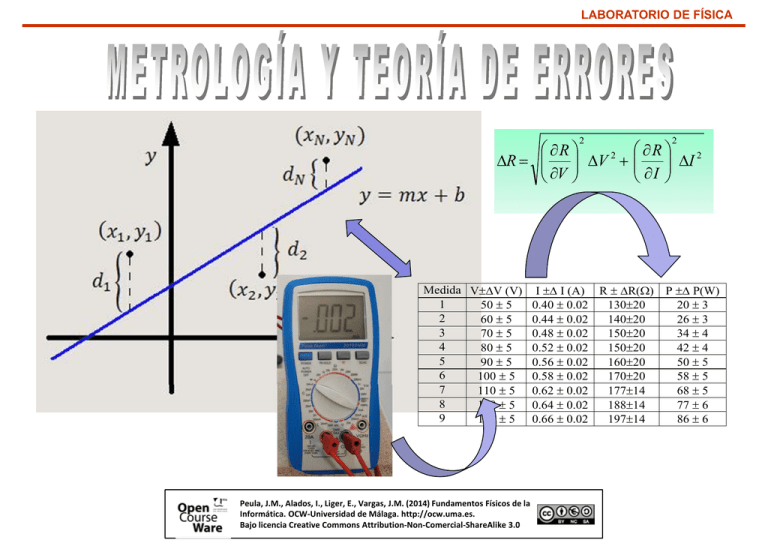
LABORATORIO DE FÍSICA
2
 R 
 V 2 
R  
 V 
Medida VV (V)
1
50  5
2
60  5
3
70  5
4
80  5
5
90  5
6
100  5
7
110  5
8
120  5
9
130  5
I  I (A) R  R()
0.40  0.02
13020
0.44  0.02
14020
0.48  0.02
15020
0.52  0.02
15020
0.56  0.02
16020
0.58  0.02
17020
0.62  0.02
17714
0.64  0.02
18814
0.66  0.02
19714
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 2
 R 

 I 2
 I 
P  P(W)
20  3
26  3
34  4
42  4
50  5
58  5
68  5
77  6
86  6
LABORATORIO DE FÍSICA
LA MEDIDA Y SU INCERTIDUMBRE
Medir
Comparar la cantidad de una magnitud física con una cantidad
de referencia que se toma como unidad.
Error
El proceso de medición siempre esta afectado por un error.
Parámetro asociado al resultado de una medida que
caracteriza la dispersión de los valores que
razonablemente se pueden asignar a la magnitud medida.
Incertidumbre
x  x  x  x  x
Errores
Sistemáticos
• Instrumentales
• Personales
• Metódicos
SENSIBILIDAD
División de escala
Intervalo más pequeño de
la magnitud medible con
un instrumento
Errores
Accidentales
Causas aleatorias o
irregulares
Incertidumbre absoluta o error absoluto
x  x  x
Precisión
Exactitud
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 LABORATORIO DE FÍSICA
Incertidumbre y cifras significativas
Incertidumbre o
error absoluto
(∆x)
x  x  x
Incertidumbre
o error relativo
(εr)
x
r 
x
Se expresa en %
Expresión de las medidas
Cifras significativas
La incertidumbre o error
absoluto sólo tendrá una cifra
significativa
La magnitud se expresa con
tantas cifras significativas
como indique su error absoluto
Expresión incorrecta
Expresión correcta
(5.328 ± 0.118) m
(5.33 ± 0.12) m
(8.4 ± 0.076) g
(8.40 ± 0.08) g
(6320 ± 257) s
(6300 ± 300) s
(32.3541 ± 0.17) V
(32.4 ± 0.2) V
(203.48 ± 0.4) mA
(203.5 ± 0.4) mA
(1.2038 ± 0.0103) Ω
(1.204 ± 0.010) Ω
Notación científica
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 95000 = 9,5 · 104
6300 ± 300 = (6.3 ± 0.3) · 103
LABORATORIO DE FÍSICA
MEDIDA DIRECTA DE UN MAGNITUD
Error o incertidumbre
nominal
Errores
Sistemáticos
Minimización
Error de sensibilidad
del aparato
 nom  Error sistemátic o
• Instrumental
• Apreciación
• Calibración
• Método medición
 sensilidad  E
E es la división de escala
 nom   sensibilidad
Procedimiento
• Inicialmente se realizan tres medidas de la magnitud física.
• Se calcula la Dispersión (diferencia entre valores extremos).
• Se compara la dispersión con el error de sensibilidad.
D0
D   nom
x
x1  x2  x3
3
 x   nom
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 x  x  x
LABORATORIO DE FÍSICA
MEDIDA DIRECTA DE UN MAGNITUD
100 D
D 
x
D   nom
Incertidumbre asociada a la
dispersión estadística
n
εD
Medidas a realizar
εD < 2 %
3
2 % < εD < 8 %
6
8 % < εD < 15%
15
εD > 15 %
50
est  x 
xi  x
i 1
2
N N 1
Desviación
estándar del
promedio
Incertidumbre de una medida directa repetida N veces
 x   est   nom
2
Aplicar factor de cobertura
Distribución
estadística
2
x  x  x
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 LABORATORIO DE FÍSICA
MEDIDA INDIRECTA DE UN MAGNITUD
Ley de propagación de errores o incertidumbres
y  f x 
2
 df 
  y     x2
 dx 
n
y  f xi ,....., xn    y 
Ejemplo

i 1
El resultado de una medida
indirecta nunca podrá tener
más cifras significativas que
las de la medida directa que
menos tenga
2
 f 
   xi 2
 xi 
2
Z m x y
a
uZ 
b
ma x
2
 Z 
 Z 
2
  y 2 
  x  
  z  
 y 
 x 
a 1
y
  x  ma x
b 2
2
a
y
 y
b 1 2
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 2
LABORATORIO DE FÍSICA
REPRESENTACIÓN DE DATOS EXPERIMENTALES
Elaboración de tablas
Medida VV (V)
1
2
3
4
5
6
7
8
9
50  5
60  5
70  5
80  5
90  5
100  5
110  5
120  5
130  5
Representación gráfica
70
R  R() P  P(W)
0.40  0.02
0.44  0.02
0.48  0.02
0.52  0.02
0.56  0.02
0.58  0.02
0.62  0.02
0.64  0.02
0.66  0.02
20  3
26  3
34  4
42  4
50  5
58  5
68  5
77  6
86  6
13020
14020
15020
15020
16020
17020
17714
18814
19714
Relación entre magnitudes
90
80
I  I (A)
90
INCORRECTO
80
CORRECTO
70
60
P (W)
P (W)
60
50
40
50
30
40
20
30
10
20
0
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70
I (A)
10
0,40
0,45
0,50
0,55
I (A)
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 0,60
0,65
0,70
LABORATORIO DE FÍSICA
REPRESENTACIÓN DE DATOS EXPERIMENTALES
Dependencia lineal
Representación gráfica
7
I (A)
1.52 ± 0.01
0.03 ± 0.02
3.01 ± 0.01
0.06 ± 0.02
4.52 ± 0.01
0.07 ± 0.02
4.60 ± 0.01
0.09 ± 0.02
6.25 ± 0.01
0.12 ± 0.02
6
Punto experimental
erróneo
5
V-V´ (V)
V-V´ (V)
V V   R I
4
3
2
1
0,02
0,04
0,06
0,10
0,12
I (A)
La ley de Ohm predice una dependencia lineal
• La variable dependiente, y, se corresponde con V-V´
• La variable independiente x, se corresponde con I
• El parámetro b, pendiente de la recta, tiene un significado
físico: es equivalente a la resistencia eléctrica, R.
0,08
Ecuación matemática
de una recta
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 y  a b x
0,14
LABORATORIO DE FÍSICA
REPRESENTACIÓN DE DATOS EXPERIMENTALES
Funciones exponeciales
y  ma x
 log y  log m  x log a
Papel semilogarítmico
log y vs x
8
7
•Eje abcisas lineal
•Eje ordenada logarítmico
RECTA
Tensión (V)
6
5
4
3
2
1
0
0
50
100
150
200
250
Papel logarítmico
Tiempo (s)
y  m xa
•Eje abcisas logarítmico
•Eje ordenada logarítmico
 log y  log m  a log x
log y vs log x
Método cuantitativo de
análisis lineal: ajuste por
mínimos cuadrados
y  a  bx
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0 RECTA
Cálculo de la ordenada en
el origen (a) y la
pendiente de la recta (b)
LABORATORIO DE FÍSICA
ANÁLISIS DE DATOS EXPERIMENTALES
Ajuste por mínimos cuadrados
y  a  bx
Dependencia lineal



Cálculo de la ordenada en el
origen (a) y la pendiente de la
recta (b)
V
Sentido físico de ambos parámetros
Cálculo de las magnitudes físicas
y su incertidumbre
Interpretación de las experiencias
Conclusiones acerca de los resultados
obtenidos en la experiencia
Peula, J.M., Alados, I., Liger, E., Vargas, J.M. (2014) Fundamentos Físicos de la Informática. OCW‐Universidad de Málaga. http://ocw.uma.es. Bajo licencia Creative Commons Attribution‐Non‐Comercial‐ShareAlike 3.0