Pruebas de Acceso a Ense˜ nanzas Universitarias Oficiales de Grado (2013) Materia:

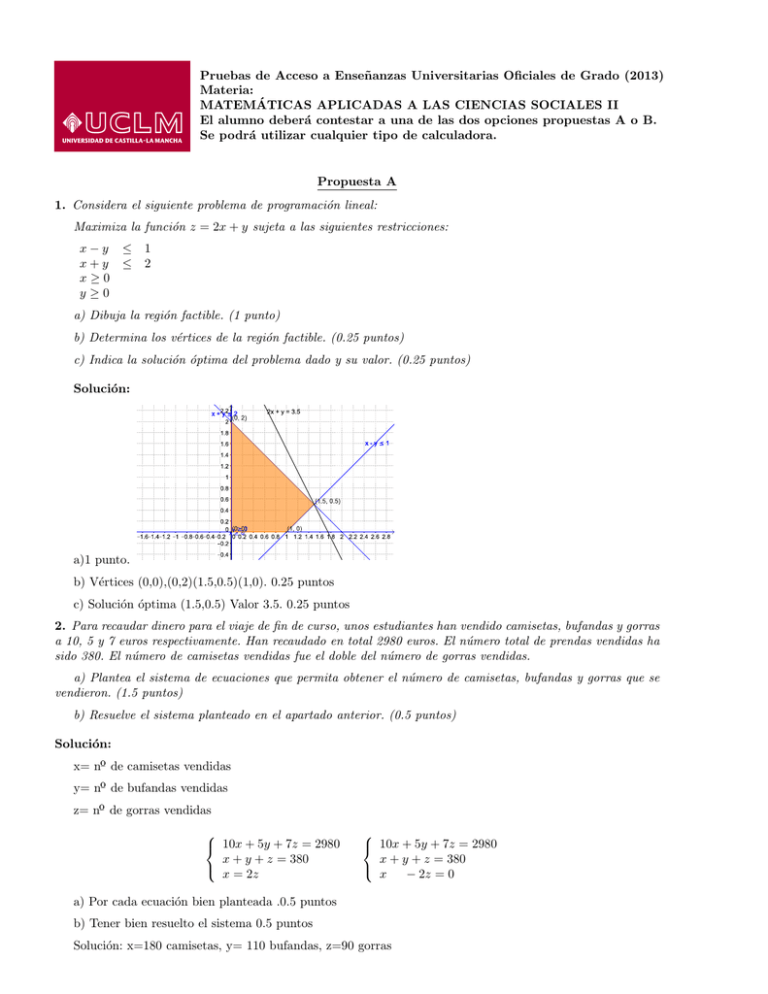
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (2013)
Materia:
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
El alumno deberá contestar a una de las dos opciones propuestas A o B.
Se podrá utilizar cualquier tipo de calculadora.
Propuesta A
1. Considera el siguiente problema de programación lineal:
Maximiza la función z = 2x + y sujeta a las siguientes restricciones:
x−y
x+y
x≥0
y≥0
≤
≤
1
2
a) Dibuja la región factible. (1 punto)
b) Determina los vértices de la región factible. (0.25 puntos)
c) Indica la solución óptima del problema dado y su valor. (0.25 puntos)
Solución:
a)1 punto.
b) Vértices (0,0),(0,2)(1.5,0.5)(1,0). 0.25 puntos
c) Solución óptima (1.5,0.5) Valor 3.5. 0.25 puntos
2. Para recaudar dinero para el viaje de fin de curso, unos estudiantes han vendido camisetas, bufandas y gorras
a 10, 5 y 7 euros respectivamente. Han recaudado en total 2980 euros. El número total de prendas vendidas ha
sido 380. El número de camisetas vendidas fue el doble del número de gorras vendidas.
a) Plantea el sistema de ecuaciones que permita obtener el número de camisetas, bufandas y gorras que se
vendieron. (1.5 puntos)
b) Resuelve el sistema planteado en el apartado anterior. (0.5 puntos)
Solución:
x= nº de camisetas vendidas
y= nº de bufandas vendidas
z= nº de gorras vendidas

 10x + 5y + 7z = 2980
x + y + z = 380

x = 2z

 10x + 5y + 7z = 2980
x + y + z = 380

x
− 2z = 0
a) Por cada ecuación bien planteada .0.5 puntos
b) Tener bien resuelto el sistema 0.5 puntos
Solución: x=180 camisetas, y= 110 bufandas, z=90 gorras
3. Se considera la función f (x) =
| − x − 1| − t si x ≤ 2
x−5
si x > 2
a) Halla el valor de t para que f sea continua en x = 2. (0.5 ptos)
b) Para t = 2, representa gráficamente la función f. (1 pto)
Solución:
a) Para que sea continua, debe coincidir el valor de la función en ese punto con sus lı́mites laterales.
Saber condiciones (0.25 puntos)
Cálculo correcto del valor, t=6 (0.25 puntos)
b)
0.5 ptos por cada trozo bien dibujado
4. Calcula los valores de los parámetros a y b para que la función f (x) = x2 + ax + b tenga un mı́nimo en el
punto (2, 1). (1.5 puntos)
Solución:
f (x = 2) = 1 ⇒ 4 + 2a + b = 1 ⇒ 2a + b = −3 (0.5 puntos)
f 0 (x) = 2x + a (0.25 puntos)
f 0 (x = 2) = 0 por tener f un mı́nimo en el punto de abscisa x = 2 (0.25 puntos)
⇒ 4 + a = 0 ⇒ a = −4 (0.25 puntos)
2a + b = −3 ⇒ b = −3 − 2a = −3 + 8 = 5 (0.25 puntos)
5. En una empresa se producen dos tipos de piezas: A y B. El 20 % son piezas del tipo A y el 80 % piezas del
tipo B. La probabilidad de que una pieza de tipo A sea defectuosa es 0.02 y de que una pieza de tipo B sea
defectuosa es 0.1.
a) Elegida una pieza al azar, ¿cuál es la probabilidad de que sea defectuosa? (0.75 puntos)
b) Se escoge al azar una pieza y resulta no defectuosa, ¿cuál es la probabilidad de que sea del tipo A? (0.75
puntos)
Solución:
a) A= Tipo A; B=Tipo B; D=defecto;ND= No defecto P(A)=1/5; P(B)=4/5
P(D/A)=0.02; P(D/B)=0.1
Plantear probabilidades (0.25 ptos)
P(D)=P(D ∩ A)+ P(D ∩ B)=P(A)*P(D/A)+P(B)*P(D/B)=0.084. (0.5 puntos)
b) P(A/ND)=P(A ∩ ND)/P(ND)=(P(ND/A)*P(A))/(1-P(D))=(0.98*0.2)/(1-0.084)=0.2139738. (0.75 puntos)
6. Se considera una muestra aleatoria de 10 consumidores mayores de edad, que en las rebajas de invierno
gastaron: 65, 72, 74, 75, 80, 81, 82, 84, 87 y 90 euros respectivamente.
a) Sabiendo que el gasto por persona, en las rebajas de invierno, sigue una distribución normal de media
desconocida y desviación tı́pica σ = 20 euros, halla un intervalo de confianza para el gasto medio poblacional
con un nivel de confianza del 95 %. (1.25 puntos)
b) Explica razonadamente cómo podrı́amos disminuir la amplitud del intervalo con el mismo nivel de confianza. (0.75 puntos)
Solución:
a) La media muestral es:
x̄ =
65+72+74+75+80+81+82+84+87+90
10
Del enunciado se deduce:
= 79 euros (0.25 puntos)
n = 10 y σ = 20 euros
1- α = 0,95 ⇒ Z α2 =1,96 (0.25 puntos)
IC= ( x̄ − Z α2
√σ
n
,
IC= (79 - 1.96 √2010 ,
x̄ + Z α2
√σ
n
79 + 1, 96
) (0.25 puntos)
√20
10
) = (66.604, 91.396) (0.5 puntos)
b) Aumentando el tamaño de la muestra. (0.75puntos)
Propuesta B

1
1. Dadas las matrices: A =  1
1
−1
3
0

1
−1

1
yB=
5
1
1
0
.
a) Calcula la matriz M = (3 · I + A2 ), donde I es la matriz identidad de orden 3. (0.75 ptos)
b) Calcula la matriz X tal que X · B = I, donde I es la matriz identidad de orden 2. (0.75 ptos)
Solución:
a)

1
A2 = A · A =  1
1
−1
3
0
 
1
1
1 · 1
1
1
 
1
1
1 = 5
1
2
−1
3
0
−4
8
−1

1
5 
2
Cálculo de A2 (0.5 puntos)


4 −4 1
M = (3 · I + A2 ) =  5 11 5 
2 −1 5
Multiplicación y suma (0.25 puntos)
b)
0.5 puntos procedimiento y 0.25 puntos por
0 1/5
X=
1 1/5
2. Una empresa produce tres tipos de bicicletas: de montaña, de paseo y estáticas. Para su fabricación cada bicicleta necesita piezas de acero, aluminio y fibra de carbono en las cantidades que se indican en la tabla siguiente:
Bicicleta de montaña Bicicleta de paseo
Bicicleta estática
Piezas de acero
2
3
1
Piezas de aluminio
6
4
6
Piezas de fibra de carbono
8
6
6
Si se dispone de 9 piezas de acero, 28 piezas de aluminio y 34 piezas de fibra de carbono:
a) Plantea el sistema que nos permita obtener el número de bicicletas de cada tipo que se podrán fabricar
utilizando todas las piezas. (1.5 puntos)
b) Resuelve el sistema planteado en el apartado anterior. (0.5 puntos)
Solución:
a)
x= nº de bicicletas de montaña fabricadas
y=nº de bicicletas de paseo fabricadas
z=nº de bicicletas estáticas fabricadas

 2x + 3y + z = 9
6x + 4y + 6z = 28

8x + 6y + 6z = 34

 2x + 3y + z = 9
3x + 7y
= 13

x + 3y
=5
Por cada ecuación bien planteada.0.5 puntos
b)
Por tener bien resuelto el sistema.0.5 puntos
Soluciones: x=2, y=1, z=2

 2x + 3y + z = 9
3x + 7y
= 13

y
=1
3. Se considera la función f (x) =
|x − t|
(x − 3)2 − 1
si x ≤ 2
si x > 2
a) ¿Para qué valor de t la función f (x) es continua en x = 2? (0.5 ptos)
b) Calcula los extremos relativos de la función f (x) en el intervalo (2, +∞). (0.5 ptos)
c) Calcula los intervalos de crecimiento y decrecimiento de la función f (x) en (2, +∞). (0.5 ptos)
Solución:
a) Para que sea continua, debe coincidir el valor de la función en ese punto con sus lı́mites laterales.
Saber condiciones (0.25 puntos)
Cálculo correcto del valor, t=2 (0.25 puntos)
b)
Saber condiciones de extremo (0.25 puntos)
Tiene un mı́nimo en (3,-1) (0.25 puntos)
c)
En (2,3) es decreciente y en (3,+∞) es creciente
(0.5 puntos)
4. En un tramo de una montaña rusa, la altura alcanzada por el vagón, medida en metros, se ajusta a la función
f (t) = t3 − 9t2 + 15t + 38, siendo t el tiempo medido en segundos, 0 ≤ t ≤ 6.
a) ¿En qué instante t, el vagón alcanza la altura máxima en ese tramo, y cuál es dicha altura? (1 punto)
b) ¿En qué instante t, el vagón alcanza la altura mı́nima en el tramo mencionado, y cuánto vale dicha altura?
(0.5 puntos)
Solución: a)
f (t) = t3 − 9t2 + 15t + 38
f 0 (t) = 3t2 − 18t + 15 (0.25 puntos)
f 0 (t) = 0 ⇔ 3t2 − 18t + 15 = 0 ⇒ t = 1 y t = 5 (0.25 puntos)
f 00 (t) = 6t − 18
f 00 (t = 1) = 6 − 18 = −12 < 0 corresponde a un máximo relativo (0.25 puntos)→ (t = 1, f (1) = 45)
En el instante t=1 el vagón alcanza su altura máxima y es de 45m (0.25 puntos)
b) f 00 (t = 5) = 6 · 5 − 18 = 12 > 0 corresponde a un mı́nimo relativo (0.25 puntos)→ (t = 5, f (5) = 13)
En el instante t=5 el vagón alcanza su altura mı́nima en ese tramo considerado y es 13m. (0.25 puntos)
5. En un colegio el 30 % de los alumnos juegan al baloncesto, el 40 % juegan al fútbol, y el 50 % juegan al fútbol
o al baloncesto o a ambos deportes.
a) Se elige un alumno al azar, ¿cuál es la probabilidad de que juegue al fútbol y juegue al baloncesto? (0.75
puntos)
b) Si elegimos un alumno al azar y juega al baloncesto, ¿cuál es la probabilidad de que juegue al fútbol? (0.75
puntos)
Solución:
a) F= jugar al fútbol; B= jugar al baloncesto; P(B)=0.30; P(F)=0.40; P (B ∪ F)=0.5
Plantear probabilidades (0.25 ptos)
P(B ∩ F)=P(B)+P(F)-P(B ∪ F)=0.3+0.4-0.5=0.2. (0.5 ptos)
b)
P(F/B)=P(F ∩ B)/P(B)=0.2/0.3=2/3 (0.75 ptos)
6. Una fábrica produce cables de acero, cuya resiliencia sigue una distribución normal de media desconocida y
desviación tı́pica σ = 10 KJ/m3 . Se tomó una muestra aleatoria de 100 piezas y mediante un estudio estadı́stico
se obtuvo un intervalo de confianza (898.04 , 901.96) para la resiliencia media de los cables de acero producidos
en la fábrica.
a) Calcula el valor de la resiliencia media de las 100 piezas de la muestra. (0.75 puntos)
b) Calcula el nivel de confianza con el que se ha obtenido dicho intervalo. (1.25 puntos)
Solución:
a) El intervalo de confianza es simétrico respecto de la media muestral. Por tanto la media muestral es:
x̄ = 898,04+901,96
= 900 KJ/m3 (0.75 puntos)
2
b)
IC = x̄ − z α2 √σn , x̄ + z α2
= (898,04 , 901, 96)
√σ
n
= 900 − z α2
√10
100
, 900 + z α2
√10
100
=
900 − z α2 , 900 + z α2 =
900 − z α2 = 898,04 ⇒ z α2 = 1,96 ⇒ El nivel de confianza es del 95 %
Escribir la fórmula del intervalo de confianza.0.25 puntos
Escribir la fórmula del intervalo de confianza con los datos del problema.0.25 puntos
Igualar el intervalo obtenido anteriormente y el dado. 0.25 puntos
Obtener z α2 = 1,96 . 0.25 puntos
Obtener que el nivel de confianza es del 95 %.0.25 puntos