ex sept06 solucion

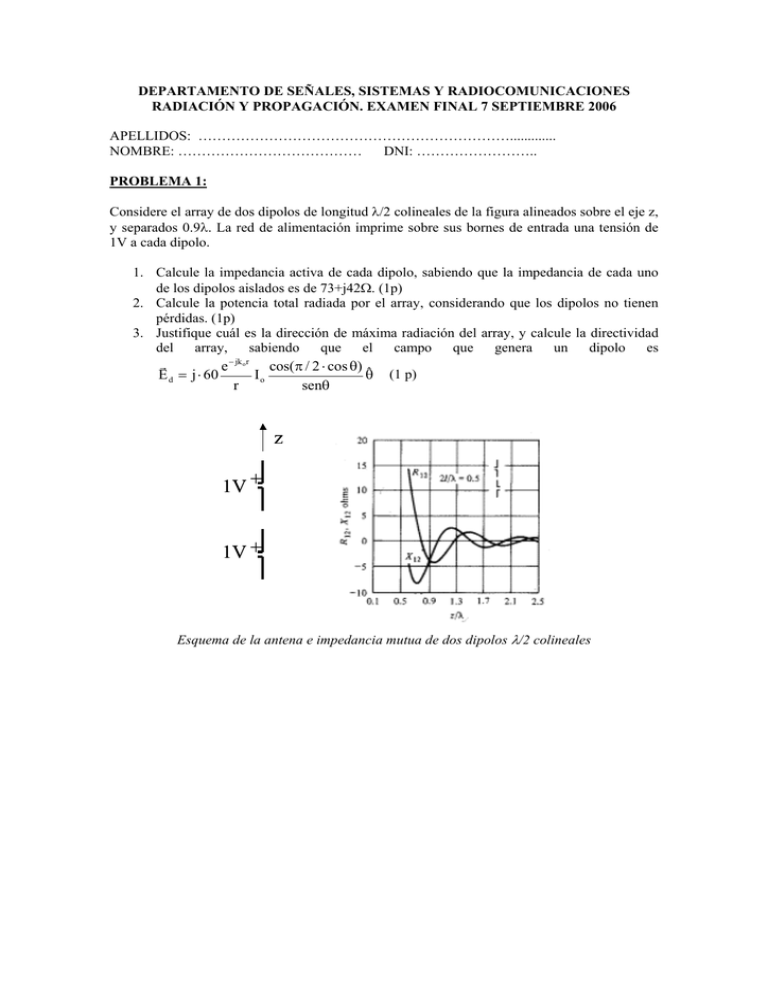
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 7 SEPTIEMBRE 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
PROBLEMA 1:
Considere el array de dos dipolos de longitud λ/2 colineales de la figura alineados sobre el eje z,
y separados 0.9λ. La red de alimentación imprime sobre sus bornes de entrada una tensión de
1V a cada dipolo.
1. Calcule la impedancia activa de cada dipolo, sabiendo que la impedancia de cada uno
de los dipolos aislados es de 73+j42Ω. (1p)
2. Calcule la potencia total radiada por el array, considerando que los dipolos no tienen
pérdidas. (1p)
3. Justifique cuál es la dirección de máxima radiación del array, y calcule la directividad
del
array,
sabiendo
que
el
campo que genera un dipolo es
r
e − jk or cos(π / 2 ⋅ cos θ) ˆ
E d = j ⋅ 60
Io
θ
r
senθ
(1 p)
z
1V +
1V +
Esquema de la antena e impedancia mutua de dos dipolos λ/2 colineales
Solución:
1. Para el cálculo de la impedancia de entrada partimos del modelo de cuadripolo, donde
las ecuaciones son:
V1 = I1 z11 + I2 z12
V2 = I1 z21 + I2 z22
donde, por la simetría del problema: V1 = V2 ; I1 = I2 y z11 = z22, con lo que queda
V1 = I1 (z11 + z12) y Zin = V1 / I1 = z11 + z12
Zin = z11 + z12 = 73 +j42 – (4+j4) = 69 + j38 Ω, donde 4+4j es la impedancia mutua de
los dos dipolos, que se observa en la gráfica para una separación entre dipolos de 0.9λ.
2. La potencia radiada por el array se puede poner como suma de las potencias radiadas
por cada uno de los dos elementos:
2
Prad
1
1 V
= P1 + P2 = 2 ⋅ I 2 ⋅ R in = 2 ⋅
⋅ 69 = 0.0111W = 11mW
2
2 Zin
donde, Zin
2
= 69 + j38
2
3. La dirección de máxima radiación es θ=90º, porque ambos dipolos están excitados con
la misma fase. Para el cálculo de la directividad hacemos:
2
4πr 2 ⋅ E max
Do =
;
2ηo Prad
siendo el campo máximo que genera el conjunto la suma de los campos que genera cada
dipolo de manera individual (en el máximo se suman los campos que genera cada
dipolo en fase), es decir 2 veces el campo máximo que genera cada uno de ellos:
E max
60 ⋅ I o
= 2⋅
=2
r
60 ⋅ V
Zin
r
operando con ηo=120π, se obtiene: Do=3.48, que en dBi es: 10 log 3.48 = 5.4 dBi
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 7 SEPTIEMBRE 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
PROBLEMA 2:
Considere un radioenlace a 30 GHz, de corta distancia (500 m) entre dos edificios altos que
utiliza como antena transmisora una bocina cónica corrugada de 5 cm de diámetro de apertura
con un error de fase s=0.8, que radia una potencia de 10 mW.
1. A partir de los anchos de haz a –3dB, estime la directividad de la bocina. (1p)
2. Si hay una densidad de lluvia en el trayecto de 25 mm/hora, calcule la densidad de
potencia incidente sobre la antena receptora situada en el segundo edificio. Considere la
bocina bien orientada (1p)
3. Como antena receptora se utiliza un reflector parabólico tipo offset. Estime el diámetro
de la apertura para conseguir una potencia recibida de –50 dBm (1p)
Diagrama universal de la bocina cónica
corrugada
Atenuación por lluvia(dB/km)
Solución:
1. Para el cálculo del ancho de haz a –3 dB, utilizamos el diagrama universal de la bocina
cónica corrugada, para la curva de s=0.8, y vamos al punto de ordenada 10-3/20=0.7, y
obtenemos: 2π(a/λ)senθ-3dB=3.7 en abcisas. De aquí despejamos el valor de θ-3dB =
0.235 rad, donde a=2.5 cm (radio de la bocina) y λ=1 cm (longitud de onda c/f). Si
pasamos el valor anterior a grados, se obtienen 13.5º. El ancho de haz a –3 dB es 2
veces este ángulo (la bocina tiene el máximo de radiación en θ=0º), obteniendo BW3dB=27º.
A partir de este valor, y para calcular la directividad, hacemos uso de la expresión
aproximada:
Do =
4π
4π
=
= 56.6 ⇒ 10 log 56.6 = 17.5dBi
2
BWE ⋅ BWH
27 ⋅ π
180
(
)
donde BWE = BWH, debido a la simetría de revolución del diagrama de radiación de las
bocinas cónicas corrugadas, y los 27º se han transformado a radianes.
2. Para calcular la densidad de potencia incidente en presencia de lluvia con intensidad de
25 mm/hora, aplicamos la expresión de la densidad de potencia, modificada por un
factor de potencia adicional debido a la atenuación que produce la lluvia.
S =
PIRE
10mW ⋅ 1017.5 /10
⋅
F
=
Fp
p
4πd 2
4π500 2
donde el factor de potencia se calcula a partir de la atenuación que produce la lluvia. La
atenuación es, según la gráfica para 25 mm/hora y 30 GHz, de 5dB/km. Como el
trayecto es de 500 metros, la atenuación total es de 2.5 dB, y el factor de potencia de:
Fp=10-2.5/10.
Operando la expresión anterior y pasando a unidades logarítmicas (10log):
<S>=-40 dB(mW/m2)
3. Para obtener el diámetro de la apertura del reflector, calculamos primero su área
equivalente como:
Pdis = S ⋅ A eq ⇒ A eq =
Pdis
= 0.1m 2
S
El área equivalente se puede escribir a partir de la superficie de la apertura del reflector
y su eficiencia de apertura. Estimando la eficiencia de apertura en 0.75, se obtiene:
2
D
A eq = 0.1m = ε ap ⋅ Sap = 0.75 ⋅ π  ⇒ D = 41.2cm
2
2
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 7 SEPTIEMBRE 2006
APELLIDOS: ………………………………………………………….............
NOMBRE: …………………………………
DNI: ……………………..
TEORÍA:
1. Una antena que posee una impedancia de entrada de 75+j20Ω y un rendimiento de
radiación de 0.8 se alimenta a través de un cable coaxial sin pérdidas de 50Ω, conectado
a un generador de 50Ω con una potencia disponible de 1W. Calcule la potencia radiada
por la antena. (1p)
Solución:
La potencia radiada se puede poner a partir del coeficiente de reflexión y del
rendimiento de radiación como:
(
2
)
Prad = Pdg 1 − ΓT ηrad = 0.75W
donde, el cuadrado del coeficiente de reflexión se obtiene como:
ΓT
2
75 + j20 − 50
=
75 + j20 + 50
2
r
e − jk o z
mV / m . Diga
2. Una antena radia en la dirección del eje z un campo E = ( x̂ + j2 ŷ)
z
cómo situaría un dipolo para conseguir la máxima potencia en recepción, y calcule las
pérdidas por desacoplo de polarización del radioenlace (1p)
Solución:
La antena transmisora genera una onda con polarización elíptica, mientras que el dipolo
receptor tiene polarización lineal. Para conseguir el máximo acoplo de potencia, hay
que situar el dipolo receptor alineado según el eje mayor de la elipse de polarización de
la onda transmitida, es decir según la dirección y. En este caso, las pérdidas por
desacoplo de polarización se obtienen como el producto escalar de los dos vectores
unitarios de polarización:
2
L despol = −10 log
x̂ + 2 jŷ
⋅ ŷ = 0.97dB
5
3. Considere un enlace up-link a 14 GHz vía satélite entre Tierra y un satélite
geostacionario (a 36000 km de la Tierra). Calcule la PIRE necesaria en el transmisor en
Tierra, para tener una relación S/N en el satélite de 20 dB, sabiendo que el satélite
utiliza un reflector de 37 dBi de ganancia, y el receptor presenta una figura de ruido de
2 dB con un ancho de banda de canal de 27 MHz. (k=1.38 10-23 J/K) (1p)
Solución:
La PIRE depende de la potencia recibida que se puede poner a partir de la Fórmula de
Friis:
Prx (dBm) = PIRE(dBm) + G RX − 20 log
4πd
. Por su parte, la potencia
λ
recibida, se puede escribir a partir de la relación S/N como:
S
(dB) = Prx (dBm) − N(dBm) ⇒ Prx (dBm) = 10 log kBTeq + S / N , donde
N
Teq=To(f-1)+Ta = 459.6 K. Operando, resulta: N=-97.7 dBm, y Prx = -77.7 dBm.
Despejando de la fórmula de Friis se obtiene: PIRE = 91.8 dBm = 61.8 dBW, donde las
pérdidas de espacio libre son de 206.5 dB
4. Explique porqué el alcance de las emisoras de Onda Media es mucho mayor durante la
noche que durante el día. (1p)
Solución:
Por la noche no existe capa D de la ionosfera, con lo que la atenuación que presenta ésta
en onda media es mucho menor. Esto hace que el alcance sea mucho mayor que durante
el día.