sol feb 10

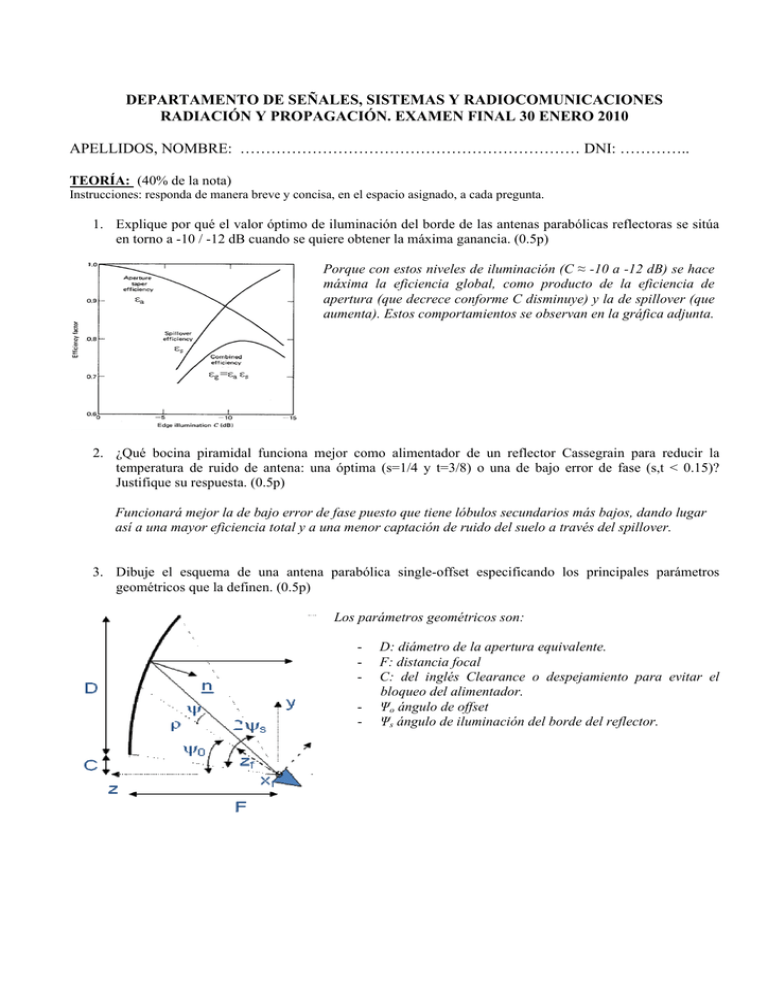
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2010
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
TEORÍA: (40% de la nota)
Instrucciones: responda de manera breve y concisa, en el espacio asignado, a cada pregunta.
1. Explique por qué el valor óptimo de iluminación del borde de las antenas parabólicas reflectoras se sitúa
en torno a -10 / -12 dB cuando se quiere obtener la máxima ganancia. (0.5p)
Porque con estos niveles de iluminación (C ≈ -10 a -12 dB) se hace
máxima la eficiencia global, como producto de la eficiencia de
apertura (que decrece conforme C disminuye) y la de spillover (que
aumenta). Estos comportamientos se observan en la gráfica adjunta.
2. ¿Qué bocina piramidal funciona mejor como alimentador de un reflector Cassegrain para reducir la
temperatura de ruido de antena: una óptima (s=1/4 y t=3/8) o una de bajo error de fase (s,t < 0.15)?
Justifique su respuesta. (0.5p)
Funcionará mejor la de bajo error de fase puesto que tiene lóbulos secundarios más bajos, dando lugar
así a una mayor eficiencia total y a una menor captación de ruido del suelo a través del spillover.
3. Dibuje el esquema de una antena parabólica single-offset especificando los principales parámetros
geométricos que la definen. (0.5p)
Los parámetros geométricos son:
-
D: diámetro de la apertura equivalente.
F: distancia focal
C: del inglés Clearance o despejamiento para evitar el
bloqueo del alimentador.
Ψo ángulo de offset
Ψs ángulo de iluminación del borde del reflector.
4. El valor de campo radiado por una antena en la dirección de máxima radiación vale 20 V/m a 100 m de
distancia ¿Qué campo radiará a 200 metros a través de un lóbulo secundario con un nivel de 20 dB por
debajo del principal? (0.5p)
En el máximo de radiación y a 200 metros, debido a que el campo se propaga como 1/r, tendremos:
20V / mx100
 10V / m
200
A través de un lóbulo secundario de -20 dB, tendremos: 10V / m 10 20 / 20  1V / m
5. Considere un array endfire formado por 7 elementos, que pueden considerarse isótropos, separados 0.4.
¿Cuánto vale el desfasaje entre elementos? (0.5p)
El array endfire presenta el máximo de radiación en θ=0. A partir de la condición del máximo se puede
obtener el desfasaje entre elementos:
  k o d cos     0    k o d  
2

0.4  0.8rad  144º
6. ¿Qué son las frecuencias críticas en propagación ionosférica? ¿Por qué se suelen utilizar frecuencias por
encima de la máxima de éstas en comunicaciones de radioaficionados de larga distancia? (0.5p)
Las frecuencias críticas son las frecuencias más altas que son reflejadas por las distintas capas
ionosféricas con incidencia vertical (fcD<fcE<fcF). Para comunicaciones a larga distancia hay que utilizar
frecuencias de HF algo más altas para que las ondas con ángulos φo elevados penetren hasta cerca de la
máxima densidad electrónica de las capas F y lleguen así más lejos. Las frecuencias óptimas de trabajo
se sitúan en OWF=0.85 MUF = 0.85 fcF sec φo
7. ¿Por qué hay zonas de “fading” durante la noche en la propagación de ondas medias de radio? (0.5p)
Porque durante la noche la práctica desaparición de la ionización de la capa D reduce la atenuación de
las frecuencias de onda media de unos 2/4 dB/km a 0.1/0.2 dB/km, permitiendo que las ondas de estas
frecuencias retornen a Tierra con amplitud suficiente como para interferir con las propias de su onda de
superficie, dando lugar, cuando ambas son de amplitudes similares, a reforzamientos y debilitamientos
intensos (fading) de la señal.
8. Dibuje el esquema, señalando de manera aproximada dimensiones eléctricas, y diga las principales
características eléctricas (forma del diagrama de radiación, polarización, directividad…), de las antenas
de tipo de Yagi-Uda (0.5p)
Por ejemplo se presenta una antena Yagi con un dipolo
plegado como elemento activo, dos varillas reflectoras y 6
elementos directores. Las dimensiones son las siguientes:
- Elemento activo: en torno a 0.47 (resonante)
- Elementos directores: en torno a 0.45 y separados entre sí
de 0.25 a 0.4.
- Los elementos reflectores en torno a .
El diagrama de radiación es unidireccional y en la dirección
del eje de la antena (en la dirección de los elementos
directores). La polarización es lineal (la propia de los dipolos
que la forman). La directividad va desde unos 7 dBi para una
Yagi de 2 elementos hasta unos 17/18 dBi cuando se diseña
con unos 30 elementos.
DEPARTAMENTO DE SEÑALES, SISTEMAS Y RADIOCOMUNICACIONES
RADIACIÓN Y PROPAGACIÓN. EXAMEN FINAL 30 ENERO 2010
APELLIDOS, NOMBRE: ………………………………………………………… DNI: …………..
PROBLEMA 1: (30% de la nota)
Se dispone de dos bocinas piramidales cónicas
corrugadas de banda C (f=6 GHz) con aperturas de 24
cm de diámetro y longitud de L=18 cm. Se dispone
también de un amplificador de la misma banda que da
una figura de ruido a un sistema receptor de 3 dB. Se
trata de diseñar un radioenlace para transmisión de
video de 8 MHz de ancho banda para comunicar las
orillas de un lago de 5 km de ancho.
1. Calcule la altura óptima de las torres
(supuestas iguales) para situar las bocinas. (1p)
2. Estime la ganancia de las bocinas a partir de
los diagramas universales (para esta bocina de
tipo escalar, con gran ángulo, no vale la
fórmula de apertura equivalente). (1p)
3. Calcule la potencia disponible del transmisor
necesaria para conseguir una S/N=26 dB, si la
temperatura de ruido de antena para el trayecto
horizontal a Tierra es de 180K (k=1.38 10-23
W/Hz/K y To=290K) (1p)
Diagramas universales de bocinas cónicas corrugadas
Solución:
1. Para calcular la altura óptima de las antenas (supuestas las dos a la misma altura), sumo
vectorialmente el campo del rayo directo con el campo del rayo reflejado y busco la altura mínima en
el que se suman en fase. La altura mínima minimiza el coste de las torres. Para la suma vectorial, con
esta distancia de 5 km, puedo asumir que el diagrama de radiación va a afectar por igual al rayo
directo y al rayo reflejado. También, con el ángulo de reflexión en el lago, puedo asumir que el
coeficiente de reflexión es -1.





2
Et  E d  E r  E d  1  e  jko R  e  jko R  1  k o R  n   
R    R 
2



En las expresiones anteriores, he hecho n=1, que corresponde a la mínima distancia entre los
recorridos del rayo reflejado y directo, y por lo tanto a la altura mínima de las antenas.
R  rref  rdir  5000 2  2h   5000 
2

2
 2.5cm  h  7.9m
2. Para estimar la ganancia de las bocinas, lo hacemos a partir de la estimación de la directividad a
través de los anchos de haz a -3dB (10-3/20=0.71). Para ello utilizamos la gráfica del diagrama de
radiación universal de las bocinas cónicas corrugadas con s 
2
a

a2
 0.8 . En abcisas obtenemos:
2L
sen  3.7 . Despejando el valor de θ, obtenemos: θ=14.2 grados. El ancho de haz a -3dB es
dos veces este valor (por la simetría del diagrama de radiación en torno a θ=0), es decir BW=28.4º.
Este ancho de haz es igual en el plano E que en el plano H por la simetría de revolución del diagrama
de radiación en las bocinas cónicas corrugadas. El rendimiento de radiación lo podemos aproximar a
1, ya que estas bocinas son metálicas. Por lo tanto:
GD
4
41253

 51.1  10 log 51.1  17.1dBi
2
BW (rad )
BW ( grados ) 2
3. Para calcular la potencia transmitida utilizaremos la fórmula de Friis. Para ello necesitamos la
potencia recibida, que se calcula a partir de la relación señal a ruido de 26dB, teniendo en cuenta tanto
la temperatura de antena como la temperatura equivalente de ruido del receptor (ojo, en la expresión
el factor de ruido debe ir en unidades lineales f=10-F/10).
N  10 logk Ta  Trx B   10 logk Ta  To  f  1B   102.8dBm
A partir de este valor, la señal recibida es: Prx = N + S/N = -76.8 dBm. Aplicando la fórmula de Friis,
considerando adaptación perfecta de impedancias y acoplo perfecto de polarización, obtenemos la
potencia transmitida. :
Prx  Ptx  20 log
4d

 2Gant  Fp  76.8dBm
Para ello, las pérdidas de espacio libre son 122 dB y el factor de propagación debido a la reflexión en
el lago supone una ganancia de 6 dB (suma en fase de rayo directo y reflejado). Las ganancias de las
bocinas son las calculadas en el apartado anterior. Operando: Ptx = 5dBm
PROBLEMA 2: (30% de la nota)
Considere el array de dos dipolos de longitud /2 paralelos separados 0.5. La red de alimentación imprime sobre
sus bornes de entrada una corriente de 1A de pico a cada dipolo (con la misma fase).
1. Calcule la impedancia activa de cada dipolo, sabiendo que la impedancia de cada uno cuando están
aislados es de 73+j30. (1p)
2. Justifique cuáles son las direcciones de máxima radiación del array, revisando para las distintas
direcciones del plano perpendicular a los dipolos, dónde las contribuciones del campo de ambos se suman
en fase. (0.5p)
3. Calcule la potencia radiada por el array (0.5p) y su directividad (1p), sabiendo que la directividad de un
dipolo /2 es de 1.64 (2.15 dBi).

e  jk o r cos( / 2  cos ) ˆ
E d  j  o
Io

2r
sen
Campo de un dipolo /2 centrado en el origen y
alineado según el eje z
Impedancia mutua de dos dipolos /2 paralelos
Solución:
1. Para calcular la impedancia de entrada hacemos uso del modelo de cuadripolo, donde I1=I2, con lo
que se obtiene:
V1  z11 I 1  z12 I 2 
V1
  Z in   z11  z12
V2  z12 I 1  z 22 I 2 
I1
El valor de z12 lo obtenemos de la gráfica de acoplos mutuos, para una separación entre elementos de
0.5, es decir, una abcisa de y/=0.5. Se obtiene en ordenadas: z12=-15-j30Ω. Sumando con el valor de
autoimpedancia del enunciado z11=73+j30Ω, se obtiene: Zin = 58Ω
2. El máximo de radiación de un dipolo alineado según el eje z se encuentra en el plano XY. La
radiación de ambos dipolos se sumará en fase en las direcciones correspondientes al eje x, por lo que
es en este eje donde se encuentra el máximo de radiación.
3. La potencia radiada calcula como la suma de las potencias radiadas de cada elemento, utilizando el
valor de la impedancia activa de 58Ω. Por lo tanto, la potencia radiada es:
1
Prad  2 I 2 Rin  58W
2
Para calcular la directividad, hacemos uso de la definición de la misma: D  4r 2
S max
Prad
, del valor de
la directividad de un dipolo aislado, de la potencia radiada por un dipolo y por el array de dos dipolos,
y de la densidad de potencia radiada por el array de dos dipolos. Para ello, en la dirección del máximo,
el campo de los dipolos se suma en fase (se multiplica por 2), por lo que la densidad de potencia se
multiplicará por 4. La potencia radiada por el dipolo será: Prad ,1dipolo  1 I 2 Rin  1 12 73  36.5W . La
2
2
directividad será:
Darray
Ddipolo

S max,array
Prad , array
S max,dipolo
Prad , dipolo
 4
36.5
36.5
 Darray  1.64  4 
 4.1  10 log 4.1  6.2dBi
58
58