VIBRACION LIBRE Y LA ECUACION DE FRECUENCIA

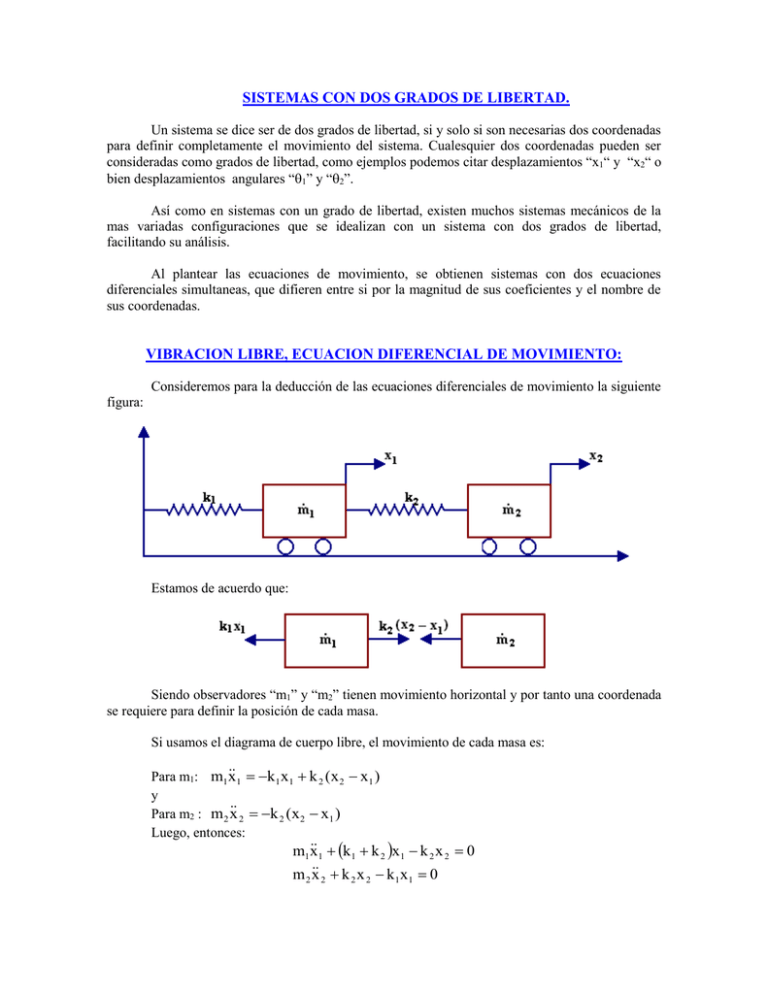
SISTEMAS CON DOS GRADOS DE LIBERTAD.
Un sistema se dice ser de dos grados de libertad, si y solo si son necesarias dos coordenadas
para definir completamente el movimiento del sistema. Cualesquier dos coordenadas pueden ser
consideradas como grados de libertad, como ejemplos podemos citar desplazamientos “x1“ y “x2“ o
bien desplazamientos angulares “1” y “2”.
Así como en sistemas con un grado de libertad, existen muchos sistemas mecánicos de la
mas variadas configuraciones que se idealizan con un sistema con dos grados de libertad,
facilitando su análisis.
Al plantear las ecuaciones de movimiento, se obtienen sistemas con dos ecuaciones
diferenciales simultaneas, que difieren entre si por la magnitud de sus coeficientes y el nombre de
sus coordenadas.
VIBRACION LIBRE, ECUACION DIFERENCIAL DE MOVIMIENTO:
Consideremos para la deducción de las ecuaciones diferenciales de movimiento la siguiente
figura:
Estamos de acuerdo que:
Siendo observadores “m1” y “m2” tienen movimiento horizontal y por tanto una coordenada
se requiere para definir la posición de cada masa.
Si usamos el diagrama de cuerpo libre, el movimiento de cada masa es:
Para m1: m1x1  k1 x1  k 2 (x 2  x1 )
y
Para m2 : m 2 x 2  k 2 (x 2  x1 )
Luego, entonces:
m1x1  k1  k 2 x1  k 2 x 2  0
m 2 x 2  k 2 x 2  k1 x1  0
Que precisamente son las ecuaciones diferenciales de movimiento acopladas y deberán ser
resueltas de forma simultánea. La solución tiene un proceso similar que se ha usado en sistemas
con un grado de libertad:
Supongamos que:
x 1  A1 sen(t  )
y
x 2  A 2 sen(t  )
Derivando dos veces:
x1   2 A1 sen( t  )
x 2   2 A 2 sen( t  )
Sustituyendo, tenemos:
k
k
1
2

 k 2  2n m1 A1 sen t    k 2 A 2 sen t    0

 2n m 2 A 2 sen t    k 2 A1 sen t    0
Y de aquí, si igualamos miembro a miembro tenemos:
(k1  k 2   n m1 )A 1  k 2 A 2  0
2
(k 2   n m 2 )A 2  k 2 A1  0
2
La solución trivial a estas ecuaciones es que A1 = A2 = 0 y tiene solución no trivial si y solo
si...
(k1+k2-n2m1)
- k2
=0
2
-k2
k2-n m2
De donde se ve que:
(k1  k 2  n m1 )(k2  n m2 )  k 2  0
2
2
2
Desarrollando y simplificando tenemos que:
m1m2 n  m1k 2  m2 (k1  k 2 )n  k1k 2  0
4
2
esta última es conocida como la ecuación característica, y como se puede observar, es una función
cuadrática en “n2” entonces:
1 
 b  b 2  4ac
2a
2 
 b  b 2  4ac
2a
2
2
En donde a = m1 m2; b = m1k2 + m2(k1 + k2); c = k1k2 y n1, n2 son las dos frecuencias
naturales que se esperaba por tanto existen dos soluciones; una asociada con n1 y la otra con n2.
Para el caso de n1 tendremos que:
(k1  k 2  1 m1 )A1  k 2 A 2  0
2
(k 2  1 m 2 )A 2  k 2 A1  0
2
debido a que n1 se puede obtener del determinante anterior, y hagamos ahora:
2
A 
A 
k2
k 2  1 m 2
1   1 
  11  

2
k2
 A 2  n 1  A 21  k 1  k 2  1 m1
donde “A11” y “A21” son las amplitudes de “m1” y “m2” respectivamente si el sistema vibra con su
primer frecuencia “1”, entonces las soluciones correspondientes a esta frecuencia son:
x 11  A11 sen(1 t  1 )
x 21  A 21 sen(1 t  1 )
o bien, usando “1”:
x 11  1A 21 sen1 t  
x 21  A 21 sen1 t  
Simultáneamente para “n2”:
A
 2   1
 A2
2

A
k2
k 2  2 m 2

 12 

2
k2
 2 A 22 k 1  k 2   2 m1
Esto implica que:
x 12   2 A 22 sen(2 t   2 )
x 22  A 22 sen(2 t   2 )
las relaciones de amplitud “1 y  2” son llamadas los modos principales de vibración.
La solución cumple para cada x(t) es entonces:
x 1 (t)  x 11  x 12
x 2 (t)  x 21  x 22
Luego:
x 1 (t)  1A 21 sen(1 t  1 )   2 A 22 sen(2 t   2 )
x 2 (t)  A 21 sen(1 t  1 )  A 22 sen(2 t   2 )
En estas ecuaciones, se tienen cuatro constantes A21, A22, 1, 2 que se determinan de las
condiciones iniciales.
CONDICIONES INICIALES.
Diferenciando “x1(t) y x2(t)” obtenemos:
x 1 (t)  11A 21 cos(1 t  )  2 2 A 22 cos(2 t   2 )
x 2 (t)  1A 21 cos(1 t  )  2 A 22 cos(2 t   2 )
Consideramos ahora las siguientes condiciones iniciales:
x1 (t  0)  x10 ;
x2 (t  0)  x20 ;
x1 (t  0)  x10
x 2 (t  0)  x 20
al sustituir, tenemos las siguientes cuatro ecuaciones que deberán resolverse para “A21, A22, 1, 2”
x10   1 A21 Sen1   2 A22 Sen 2
x 20  A21 Sen1  A22 Sen 2
x10  w1  1Cos1  w2  2 A22 cos 2
x 20  w1 A21Cos1  w2 A22 Cos 2
SISTEMA TORSIONAL CON DOS GRADOS DE LIBERTAD.
Como otro ejemplo, el sistema torsional de la sig. figura, consiste en dos discos, cada uno
con un momento de inercia de masa, unidos por un resorte torsional y fijos a una pared rígida por
otro.
y
y
x
+1
K11
+2
x
K2 (2 - 1)
z
+2
K2 (2 - 1)
z
Si se desplazan los discos alrededor del eje del eje de las z y se liberan, el sistema vibrara
torsionalmente alrededor del eje de las z, y las coordenadas generalizadas que describen el
movimiento de los discos y la distorsión de los resortes, serán 2 y 1.
Las ecuaciones de movimiento para los desplazamientos angulares son,
 k 11  k 2 ( 2  1 )  I11
 k (   )  I 
2
2
1
2
2
Para la vibración en modo principal,
1 = 1 sen  t
2 = 2 sen  t
La fracción modal 2 /1 es
Y esto nos da una ecuación de frecuencia
Esta es otra vez cuadrática en , con dos raíces.
La existencia de una ecuación de frecuencia involucrando las constantes físicas del sistema,
las raíces de la cual son valores característicos o frecuencias naturales, es típica de los sistemas con
grado múltiple de libertad. Para dos grados de libertad, es fácil establecer una ecuación de
frecuencia y buscar algebraicamente los valores característicos. Esto se vuelve crecientemente
difícil para grados de múltiple libertad, ya que aumente el orden de la ecuación de frecuencia con el
numero de grados de libertad. Para tres grados de libertad, la ecuación de frecuencia tendrá tres
raíces, para cuatro grados de libertad, la ecuación de frecuencia será una ecuación de cuarto orden
para , y así sucesivamente.
Para cualquier numero mayor, deberemos buscar un medio para encontrar los valores
característicos de la ecuación de frecuencia sin conocer la propia ecuación de frecuencia. El
determinar la ecuación de frecuencia explícitamente, viene a ser un trabajo arduo, y existen otros
modos de encontrar las raíces de las ecuaciones algebraicas, numéricamente. No obstante, es
importante reconocer que cuando usamos métodos numéricos para determinar los valores
característicos de un sistema de varios grados de libertad, estos valores característicos son las raíces
de una ecuación de frecuencia que no hemos determinado, pero que, sin embargo, existe.
MODOS Y FRACCIONES MODALES
Un modo es una descripción de movimiento. Existen varias clases de modos, muchos con
una frase modificaste, tales como el primer modo, el segundo modo, un modo principal o un modo
acoplado, todos los cuales describen una manera particular de movimiento.
A una frecuencia natural, un sistema vibratorios se mueve de un modo principal. Este modo
se denomina también un modo natural. Si la amplitud de movimiento de una masa tiene una unidad
de desplazamiento, se dice que el modo esta normalizado o se le denomina simplemente un modo
normal. Todas estas descripciones significan la misma cosa, que todas las partes del sistema tienen
el mismo movimiento armónico, con desplazamientos máximos en tiempos idénticos y velocidades
máximas en otros tiempos idénticos. El numero de modos principales que existan, corresponderá al
numero de grados de libertad.
Las coordenadas que se usan para describir el movimiento, describen también el modo.
Estas coordenadas no se establecen en cantidades absolutas, sino como relaciones numéricas. Esto
es, se fija el valor de una coordenada con relación a todas las otras, para cualquier otro modo dado,
y el valor absoluto de cualquier coordenada determina el valor de todas las demás coordenadas.
Como ejemplo, el valor de A1 / A2 y de 1 / 2 establece los modos de movimiento para
los dos sistemas que hemos considerado. No existe diferencia en lo que realmente sean los valores
absolutos de 2, 1, A1 o A2, ya que lo que fija el modo es el valor relativo de una con respecto a
otra. Para encontrar el modo de una valor especifico de , se sustituye simplemente ese valor en la
ecuación de movimiento, con la fracción modal.
Cuando nos referimos a la fracción modal para un valor característico dado, se acostumbra
indicarlo con un índice dentro del paréntesis. Este no deberá confundirse con un exponente, pues no
lo es. Se usa un índice (1) para el primer modo, un índice (2) para el segundo modo, un índice (i)
para el modo i-esimo, etc.
A2(1)
A(1) =
=
A1(1)
k1+k3- m1
A2(2)
A(2) =
=
A1(2)
k1+k3- m1
k3
k3
Si uno de los modos tiene un desplazamiento de una unidad, entonces los modos son
normalizados y la fracción modal tiene el mismo valor numérico que el de la otra coordenada.