Efecto fotoeléctrico

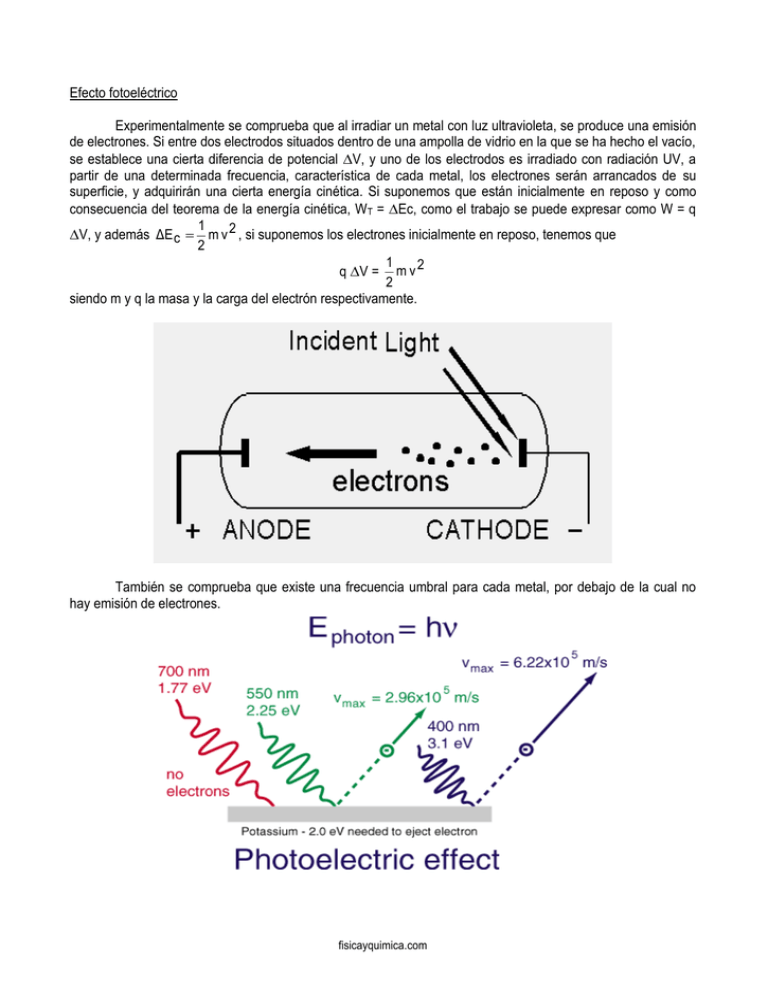
Efecto fotoeléctrico
Experimentalmente se comprueba que al irradiar un metal con luz ultravioleta, se produce una emisión
de electrones. Si entre dos electrodos situados dentro de una ampolla de vidrio en la que se ha hecho el vacío,
se establece una cierta diferencia de potencial V, y uno de los electrodos es irradiado con radiación UV, a
partir de una determinada frecuencia, característica de cada metal, los electrones serán arrancados de su
superficie, y adquirirán una cierta energía cinética. Si suponemos que están inicialmente en reposo y como
consecuencia del teorema de la energía cinética, WT = Ec, como el trabajo se puede expresar como W = q
1
V, y además ΔE c  m v 2 , si suponemos los electrones inicialmente en reposo, tenemos que
2
1
q V = m v 2
2
siendo m y q la masa y la carga del electrón respectivamente.
También se comprueba que existe una frecuencia umbral para cada metal, por debajo de la cual no
hay emisión de electrones.
fisicayquimica.com
Interpretación
Einstein consideró que la radiación electromagnética se emitía y propagaba de forma discreta.
Así, cuando un cuanto de radiación (fotón) de energía E = h (h es la constante de Planck, cuyo valor
es h = 6,624  10-34 J s, y  es la frecuencia del fotón) choca con un electrón del metal, es absorbido,
y si la energía que tiene es suficiente, puede arrancar al electrón del metal.
La existencia de una frecuencia umbral, 0, indica la energía mínima h0 necesaria para
arrancar un electrón. Esta energía es la correspondiente a los electrones cuya energía cinética
después de ser arrancados es 0, es decir, aquellos que al ser arrancados de la superficie del metal
quedan en reposo. Esta energía mínima, característica de cada metal, recibe el nombre de función
trabajo o trabajo de extracción,
WL = h0
La energía cinética máxima de los electrones emitidos por el metal puede calcularse como la
diferencia entre la energía absorbida por el fotón (que es la energía total del fotón que es transmitida
sin pérdidas al electrón) y el trabajo de extracción,
Ec máx = h - WL= h - h0
Ejemplos
1. La frecuencia umbral del potasio en el efecto fotoeléctrico es 4,5  1014 Hz. Determinar la velocidad
máxima de los electrones emitidos cuando se hace incidir sobre él luz cuya frecuencia es de 6  1014
Hz. Datos: h = 6,63  10-34 J  s ; me = 9,1  10-31 kg
solución:
Que la frecuencia umbral sea 4,5  1014 Hz nos indica que cualquier radiación de frecuencia
inferior a ésta, no será capaz de arrancar ningún electrón de la superficie del potasio. Para radiaciones
de frecuencia igual a la indicada, dejará a los electrones con una velocidad “nula” en la superficie del
metal, por lo que será necesaria una radiación de frecuencia superior a la umbral para arrancar
electrones.
1
Ec máx = m v 2 = h - h0
2
2 h (  - 0 )
despejando v, nos queda que m v 2  2 h ( -  0 ) y entonces v 
m
y sustituyendo los valores numéricos tenemos que
v
unidades:
2  6,63 10-34 J  s  ( 6  1014 Hz - 4,5  1014 Hz )
J  s  Hz
=
kg
- 31
9,1 10
J  s  s -1
=
kg
kg
J
=
kg
Nm
=
kg
fisicayquimica.com
= 4,67  105 m/s
kg  m  s - 2  m
=
kg
m
m2
=
s
s2
2. El trabajo de extracción de un electrón para el sodio es de 2,5 eV. Calcula,
a) la frecuencia umbral
b) la longitud de la luz incidente para que se produzca el efecto fotoeléctrico en dicho metal.
Datos: h = 6,63  10-34 J  s ; 1 eV = 1,6  10-19 J ; c = 3  108 m  s
solución:
a) como WL = h 0 tenemos que 0 =
WL
=
h
1,6  10 -19 J
1 eV
= 6  1014 Hz, es decir, que
34
6,63 10
J s
2,5 eV 
ésta es la frecuencia mínima con la que deberá ser radiado el sodio para que los electrones de su
superficie queden libres. Si queremos además que adquieran cierta velocidad, deberán ser
radiados con una radiación de frecuencia superior a la frecuencia umbral.
b) como tenemos que c =    podemos despejar  quedando
c 3  10 8 m  s -1
=
= 5  10-7 m = 0,5 m = 500 nm,
ν
6  1014 s -1
siendo ésta la mayor longitud de onda con la que podemos radiar el sodio para poder extraer
electrones de su superficie (a mayor frecuencia, menor longitud de onda)
λ
fisicayquimica.com