Instituto Profesional de Chile Ingeniería en Industrias Cálculo

Instituto Profesional de Chile
Ingeniería en Industrias
Cálculo
Modulo Nº 2
Integración triple y cambio de coordenadas
INTEGRALES
1. Objetivo del modulo

Calcular integrales triples

Aplicar cambio de coordenadas al calcular integrales
2. Desarrollo de Contenidos
INTEGRAL TRIPLE
Las siguientes figuras ilustran algunos ejemplos de como se pueden efectuar tales
subdivisiones en virtud de la propiedad aditiva de conjuntos:
La definición de integral triple es análoga a la de integral doble. En el caso más simple
consideremos una caja rectangular R acotada por 6 planos x= a0, x= a1, y = b0, y = b1, z
= c0, z = c1; y sea u = f(x,y,z) una función de tres variables definida en todo (x,y,z) de R.
Subdividimos el espacio en cajas rectángulares mediante planos paralelos a los planos
coordenados. Sean B1, B2,......, Bn aquellas cajas de la subdivisión que contienen puntos
de R.
z
z = c1
c1
Bi
R
co
b0
0
a0
a1
x
b1
y
Designaremos con V(Bi) el volumen de la i-ésima caja Bi.
Elegimos un punto Pi(i, i, i) en Bi, esta elección se puede hacer en forma arbitraria.
n
La suma
 f (i, i, i).V(Bi) es una aproximación de la integral triple.
i 1
La norma de subdivisión es la longitud de la mayor diagonal de las cajas B1, B2,....., Bn.
Si las sumas anteriores tienden a un límite cuando la norma de la subdivisión tiende a
cero y para elecciones arbitrarias de los puntos Pi, a este límite lo llamaremos la
INTEGRAL TRIPLE DE f SOBRE R
La expresión:  f ( x, y, z). dV se utiliza para representar el límite.
R
Así como la integral doble es igual a dos integrales iteradas, también la integral triple es
igual a tres integrales iteradas.
Para
el
caso
de
la
caja
rectángular
R
obtenemos:
a1 b1 c1
 f (x, y, z).dV  a b c f (x, y, z).dz.dy.dx
0
0
0
R
Suponemos ahora que una región S está limitada por los planos x = a0; x = a1; y = b0; y
= b1 y por las superficies z = r(x,y), z = s(x,y).
La integral triple se puede definir de igual forma
TEOREMA
Sea S una región definida por las desigualdades:
S:{P(x,y,z)/a  x  b; p(x)  y  q(x); r(x,y)  z  s(x,y)
donde las p ; q ; r y s son continuas. Si f es una función continua en S, tenemos:

S
f ( x, y, z).dV 
a1 q ( x ) s( x , y )
a p r
0
(x)
f ( x, y, z).dz.dy.dx
( x , y)
Las integrales iteradas se efectúan considerando todas las variables constantes, excepto
aquella respecto a la cual se integra. Este concepto se puede extender a n variables.
CAMBIO DE VARIABLE EN LAS INTEGRALES MULTIPLES
Sea
 f (x, y).dx.dy
de donde
R
inversa
J
única
dada
por:
 x  (u , v)
(1) y que esta transformación posee una

 y   ( u , v)
u  u ( x, y)

 v  v ( x , y)
por
lo
que
el
Jacobiano
de
(1)
 ( ,  )  ( x , y )

0
 ( u , v )  ( u, v )
Al recinto R del plano x, y le corresponde un recinto R en el plano u, v.
Haciendo entonces una partición en R con rectas paralelas a los ejes u, v; le
corresponde en el plano x, y una partición de R por curvas continuas dadas por (1).
v
y
R
Ri
Ri
R
u
x
A un subrecinto Ri de R le corresponde un subrecinto Ri de R.
Queremos encontrar como se transforma cada elemento rectangular Ri en el elemento
curvilíneo
Ri correspondiente. Para mejor ilustración ampliaremos el dibujo de ambos recintos:
y
x=(ui+h; vj+k)
y=(ui+h,vj+k)
vj+k
Ri
Ri
x=(ui+h;
vj)
k
v
y=(ui+h,
v
h
vj
x=(ui; vj+k)
y=(ui, vj+k)
u
ui
x=(ui; vj)
y=(ui, vj)
ui + h
x
Buscamos la relación que existe entre las áreas de Ri y Ri ; para lo cual podemos
considerar a Ri compuesto por dos triángulos iguales; lo mismo que a Ri.
Para una partición con   suficientemente pequeña, podemos considerar a los
triángulos curvilíneos de Ri como planos, siendo el área de cada uno de ellos:
 (u i , v, ) (u i  h, v, ) (u i , v,  k ) 
 (u i , v, ) h.u (u i , v, ) k.v (u i , v, ) 
A(R ) 1 
1

  (u i , v, )  (u i  h , v, )  (u i , v,  k )   (u i , v, ) h. u (u i , v, ) k. v (u i , v, )
2
2
2
 1

 1

1
1
0
0
Esta ultima expresión resulta de restar a los elementos de la segunda y tercera columna,
los de la primera y aplicando Taylor (despreciando los términos de orden superior al
primero) es:
Desarrollando por los elementos de la tercera fila, es:
A(R ) 1  h.u (u i , v j ) k.u (u i , v j )  h.k
 

2
2 h. u (u i , v j ) k. u (u i , v j ) 2
 u (u i , v j ) u (u i , v j )  h.k (, ) h.k (, )

J
 (u , v )  (u , v ) 
2  ( u , v)
2 ( u , v)
u
i
j 
 u i j
A(ri) = h . k . J = u . v . J = A(Ri) J
(, )
Recordando la definición de integral
( u , v)
doble
n
f
(
x
,
y
)
dx
.
dy

lim
f ( xi, yi).A(ri) y como f(x,y) = f[(u,v); (u,v)] = F(u,v)


 0i 1
R
será
(, )
 f (x, y)dx.dy   F(u, v).J.du.dv   F(u, v). (u, v) .du.dv
R
R
R
con lo que hemos obtenido la relación que liga las variables (x,y) con (u,v).
en la cual el signo debe escogerse de tal manera que la distancia no resulte negativa.
Transformación de Coordenadas Cartesianas (x,y) a Coordenadas Polares
3
r
y
( r,  )
2
1
r
r32
r1
x
r=r1
r=r2
r=r3
4

1
1
2
3  4 
y
P(x,y
)
y
r
0<r<+ 
0    2

O
x
 x  r. cos 

 y  r. sen 
 r. cos2   r. sen2   r  0 en
todo punto distinto del O (0,0)
x
x , y  
J
r ,  
x
r
y
r
x
  cos 
y
sen 

 r. sen 

r. cos 
r   x 2  y 2

Geométricamente vemos que es : 
y
  arctg


x
Coordenadas cilíndricas:


2
2
x

r
cos

r  x  y

 y  r sen  o    tan 1 xy
z z

 z  z

z
{

P
z
O
x
y
r

y
x
Coordenadas esféricas
Relación con coordenadas cartesianas:
(x,y,z)
(r, z)

 r  x2  y2  z2

y
   tan 1 x


1
z
  cos  x 2  y 2  z 2 

3. Evaluación.
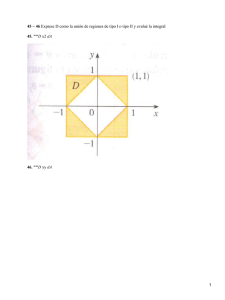
1.- En las figuras se muestra la región R. Determine si debe usar coordenadas polares o
rectangulares y escriba la expresión para  f ( x, y )dA como una integral iterada,
R
donde f ( x, y) es una función continua.
a)
2 2
RESPUESTA:
  f (r cos , r sin  )r dr d ,
0 0
2 2
b)
RESPUESTA:.,
  f ( x, y) dy dx ,
2 x
2 5
c)
RESPUESTA:
  f (r cos , r sin  )r dr d
0 2
2.- Evalue la integral dada, pasando a coordenadas polares:
a)
 xdA , donde R es el disco con centro en el origen y radio 5.
R
RESPUESTA. 0
b)

R
xydA , donde R es la región del primer cuadrante, que se encuentra entre los
círculos x 2  y 2  4 y x 2  y 2  25
c)
 e
D
 x2  y2
RESPUESTA.
609
8
dA, donde D es la región limitada por el semicírculo x  4  y 2 y el eje y.
RESPUESTA.

2
1  e 
4
3.-Utilice una integral doble para hallar el área de la región:
a) Un pétalo de la rosa r  cos 3
b)
La región interior a la lemniscata r 2  4 cos2
RESPUESTA.

12
RESPUESTA. 4
4.-Utilice las coordenadas polares para hallar el volumen del sólido dado en cada uno de
los incisos siguientes:.
a) Debajo del paraboloide z  x 2  y 2 y arriba del disco x 2  y 2  9
RESPUESTA.
81
2
b) Una esfera de radio a
RESPUESTA.
4 3
a
3
c) Arriba del cono z  x 2  y 2 y debajo de la esfera x 2  y 2  z 2  1
RESPUESTA.
2 
1 
1


3 
2
d) Interior al cilindro x 2  y 2  4 y al elipsoide 4x 2  4 y 2  z 2  64
RESPUESTA.
8
64  24 3
3


4. Bibliografía
1. Larson, Roland. “Cálculo y Geometría Analítica”, McGraw Hill, Quinta edición,
España, 1997, Volúmenes uno y dos.
2. Leithold, Louis. “Cálculo con Geometría Analítica”, Harla, sexta edición, 1992.
3. Swokoswski, Earl. “Cálculo con Geometría Analítica”, Editorial Iberoamérica,
segunda edición, 1989.
4. Ayres, Frank. Mendelson, Elliott. “Cálculo”, Schaum McGraw Hill, cuarta edición,
Colombia, 2003.
5. Thomas, George. Finney, Ross. “Cálculo con geometría analítica”, Addison-wesley
iberoamericana, U.S.A., 1987.
6. Purcell, Edwin. Varberg, Dale. “Cálculo”, Pearson educación (Prentice Hall), sexta
edición, México, 1992.