UNIVERSIDAD PONTIFICIA BOLIVARIANA TALLER # 1 DE GEOMETRÍA YTRIGONOMETRÍA

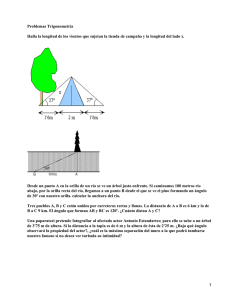
UNIVERSIDAD PONTIFICIA BOLIVARIANA
TALLER # 1 DE GEOMETRÍA YTRIGONOMETRÍA
PLANTEE Y RESUELVA LOS SIGUIENTES PROBLEMAS:
1. Una escalera de 6 m de largo descansa sobre la pared de un edificio. Si el ángulo entre la
escalera y el edificio es de 22◦, ¿a qué distancia del edificio está la parte inferior de la
escalera?
2. En un parque dos jóvenes de 1,7 m de alto se encuentran separados por una distancia de
180 m. Si uno de ellos ve un globo elevado, exactamente arriba de él, y el otro lo ve con un
ángulo de elevación de 63◦, ¿cuál es la altura del globo, respecto al suelo?
3. El cordón de una cometa se encuentra tensionado y forma un ángulo de 54◦ 20´ con la
horizontal. Encuentre la altura de la cometa, respecto al suelo, si el cordón mide 100 m y
el extremo del cordón se sostiene a 1,5 m del suelo?
4. El ángulo de elevación a la parte superior del Empire State de Nueva York, desde una
distancia de 1609 m de la base del edificio, se ha determinado que es de 11◦ sobre el nivel
del piso. ¿Cuál es la altura del Empire State?
5. Desde la parte superior de un faro de 200 pies de altura, el ángulo de depresión hasta un
barco sobre el océano es de 23◦. ¿A qué distancia está el barco de la base del faro?
6. Una escalera de 20 pies está apoyada contra un edificio, de tal manera que el ángulo entre
el piso y la escalera es de 72◦. ¿Qué altura alcanza la escalera sobre el piso?
7. Una escalera de 20 pies está apoyada contra un edificio. Si la base de la escalera está a 6
pies de la base del edificio, ¿cuál es el ángulo de elevación de la escalera? ¿Qué altura
alcanza la escalera sobre el edificio?
8. Un árbol de 96 pies proyecta una sombra de 120 pies de largo. ¿Cuál es el ángulo de
elevación del sol?
9. Un cable guía de 600 pies está sujeto a la parte superior de una torre de comunicaciones.
Si el cable forma un ángulo de 65◦ 38” con el suelo, ¿cuál es la altura de la torre?
10. Un depósito de agua está a 325 pies de un edificio. Desde una ventana del edificio se
observa que el ángulo de elevación hasta la parte superior del depósito es de 39◦ 48´ y el
ángulo de depresión a la parte inferior es de 25◦. ¿Cuál es la altura del depósito? ¿A qué
altura está la ventana?
11. Un aeroplano vuela a la altura de 5150 pies directamente por encima de una carretera
recta. Dos automovilistas están manejando automóviles sobre la carretera en lados
opuestos del aeroplano. Si el ángulo de depresión de un automóvil es de 35◦ y de 52◦ el del
otro, ¿a qué distancia están los automóviles entre sí?
12. Si ambos automóviles del ejercicio anterior están a un solo lado del aeroplano y si el ángulo
de depresión a uno de ellos es de 38◦ y al otro de 52◦. ¿a qué distancia están entre sí los
automóviles?
13. Para estimar la altura de una montaña sobre una llanura, se encuentra que el ángulo de
elevación a la cima de la montaña es de 32◦. Mil pies más cerca de la montaña sobre la
llanura se determina que el ángulo de elevación es de 35◦. Estime la altura de la montaña.
14. Desde lo alto de un edificio que mira al mar, un observador divisa una lancha que navega
directamente hacia el edificio. Si el observador está a 100 pies sobre el nivel del mar y el
ángulo de depresión de la lancha cambia de 25◦ a 40◦ durante el período de observación.
Calcule la distancia que recorre la lancha.
15. Una caja rectangular tiene dimensiones 8x6x4 cm. Calcule el ángulo formado por una
diagonal de la base y la diagonal de la caja.
16. Desde un punto P situado a nivel del suelo, el ángulo de elevación de la parte alta de una
torre es de 26◦ 50´. De un punto que está 25 m más cercano a la torre y en la misma línea
con P y la base de la torre, el ángulo de elevación de la parte alta es de 53◦ 30´. Calcule la
altura de la torre.
17. Una antena está instalada en el techo de una bodega de 16 pies de alto. Desde un punto P
a nivel del suelo y que está a 10 pies de un punto Q que está directamente bajo la antena,
las visuales a la parte inferior y superior de ésta forman un ángulo de 12◦. Calcule la
longitud de la antena.
18. Un edificio proyecta una sombra de 56 m cuando el ángulo de elevación del sol es de 24◦
11´23”. Calcule la altura del edificio.
19. Uno de los lados congruentes de un triángulo isósceles mide 14 cm y los ángulos de la
base miden 36◦ 45´. ¿Cuál es el área del triángulo?
20. Dos aviones parten de un mismo punto; el primero hacia el norte con velocidad de 48 km/h
y el segundo hacia el este con velocidad de 538 km/h. Después de dos horas, ¿a qué
distancia se encuentra uno del otro?
21. Un hombre de 1,70 m de estatura está de pie sobre el techo de un edificio y
observa un
punto sobre el pavimento de la calle. El ángulo de depresión de los pies del hombre es de
24º, mientras que el ángulo de depresión de su cabeza es de 25º. Calcular la altura del
edificio y la distancia del pie del edificio al punto observado.
22. Una escalera se coloca en el muro de una casa, de tal manera que sobresale 1 m. arriba
de la orilla del techo, que tiene una altura de 23,5 m. La escalera forma un ángulo de 70º
con el piso. ¿Cuál es la longitud de la escalera? ¿Qué distancia hay entre el muro y la base
de la escalera?
23. Para una nueva carretera debe excavarse un túnel bajo una montaña que mide 260 p. de
altura. A una distancia de 200 p de la base de la montaña el ángulo de elevación es de 36º.
De una distancia de 150 p. en el otro lado, el ángulo de elevación es de 17º. Calcular la
longitud del túnel.
24. Una escalera eléctrica debe transportar a una altura del piso de 20 pies, con un ángulo de
elevación de 25º. ¿Qué longitud tendrá la escalera?
25. Cuando se observa una torre desde lo alto de un edificio de 50 p. de altura, el ángulo de
elevación es de 59º, cuando se observa desde el pie del edificio, el ángulo de observación
es de 62º. ¿A qué distancia están las 2 estructuras ?Calcular la altura de la torre.
26. Una palma proyecta una sombra de 18 m de largo. Si el ángulo que se forma desde la
punta de la sombra hasta el punto más alto es de 48º, ¿Cuál es la altura de la palma?
27. Desde un punto situado a 29,4 m de una iglesia, los ángulos de elevación de la base y la
parte superior del campanario son 35,8º y 52,6º respectivamente. Encontrar la altura del
campanario, es decir, la distancia de su base a la parte superior.
28. Una estatua de 8.9 metros de altura se sitúa sobre un pedestal. Si desde un sitio
a 48 metros del pie del pedestal se observa el extremo superior de la estatua con
un ángulo de elevación de 26°, ¿cuál es la altura del pedestal?
29. Desde un punto A en el suelo, el ángulo de elevación a la parte superior de un
edificio es de 22º. Desde un punto B 60 m más cerca del edificio, el ángulo de
elevación es de 34º. Determine la altura del edificio.
30. El cordón de una cometa se encuentra tensionado y forma un ángulo de 54◦ 20´ con la
horizontal. Encuentre la longitud del cordón si la cometa se encuentra a una altura de 98 m
y el cordón se sostiene a 1,5 m del suelo