Análisis-insumo-producto-LEONTIEF11

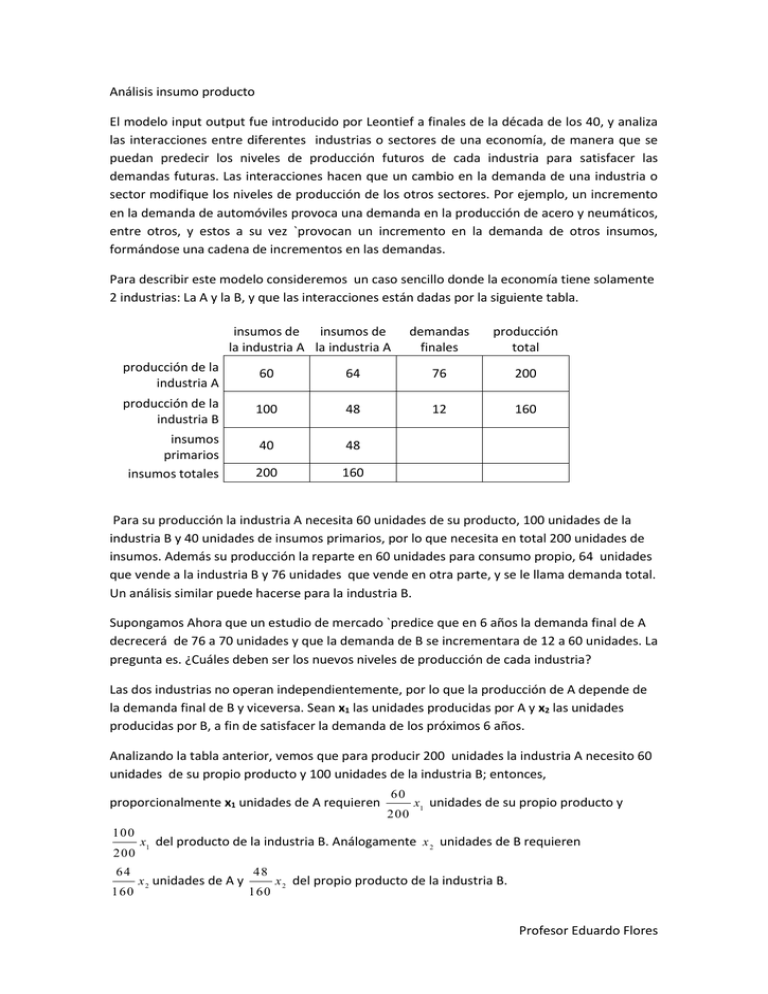
Análisis insumo producto
El modelo input output fue introducido por Leontief a finales de la década de los 40, y analiza
las interacciones entre diferentes industrias o sectores de una economía, de manera que se
puedan predecir los niveles de producción futuros de cada industria para satisfacer las
demandas futuras. Las interacciones hacen que un cambio en la demanda de una industria o
sector modifique los niveles de producción de los otros sectores. Por ejemplo, un incremento
en la demanda de automóviles provoca una demanda en la producción de acero y neumáticos,
entre otros, y estos a su vez `provocan un incremento en la demanda de otros insumos,
formándose una cadena de incrementos en las demandas.
Para describir este modelo consideremos un caso sencillo donde la economía tiene solamente
2 industrias: La A y la B, y que las interacciones están dadas por la siguiente tabla.
insumos de insumos de
la industria A la industria A
demandas
finales
producción
total
producción de la
industria A
60
64
76
200
producción de la
industria B
100
48
12
160
insumos
primarios
insumos totales
40
48
200
160
Para su producción la industria A necesita 60 unidades de su producto, 100 unidades de la
industria B y 40 unidades de insumos primarios, por lo que necesita en total 200 unidades de
insumos. Además su producción la reparte en 60 unidades para consumo propio, 64 unidades
que vende a la industria B y 76 unidades que vende en otra parte, y se le llama demanda total.
Un análisis similar puede hacerse para la industria B.
Supongamos Ahora que un estudio de mercado `predice que en 6 años la demanda final de A
decrecerá de 76 a 70 unidades y que la demanda de B se incrementara de 12 a 60 unidades. La
pregunta es. ¿Cuáles deben ser los nuevos niveles de producción de cada industria?
Las dos industrias no operan independientemente, por lo que la producción de A depende de
la demanda final de B y viceversa. Sean x1 las unidades producidas por A y x2 las unidades
producidas por B, a fin de satisfacer la demanda de los próximos 6 años.
Analizando la tabla anterior, vemos que para producir 200 unidades la industria A necesito 60
unidades de su propio producto y 100 unidades de la industria B; entonces,
proporcionalmente x1 unidades de A requieren
100
200
64
160
60
200
x1 unidades de su propio producto y
x1 del producto de la industria B. Análogamente x 2 unidades de B requieren
x 2 unidades de A y
48
160
x 2 del propio producto de la industria B.
Profesor Eduardo Flores
Las siguientes ecuaciones indican cómo se repartirá la producción de cada una de las industrias
x1 
x2 
60
200
x1 
100
200
64
160
x1 
48
160
x 2  70
x 2  60
La producción de x1 unidades de A se reparte en
64
160
60
200
x1 para consumo propio y
x 2 unidades para el consumo de la industria B y otra 70 unidades para satisfacer la
demanda final. Análogamente se explica la distribución de x2
El sistema anterior fue de escribirse en forma matricial
X  AX  D
 x1 
 70 
 es la matriz de producción, D  
 es la matriz de demanda y finalmente
 x2 
 60 
Donde X  
 60
 200
A
 100
 200
64 
160 
 la cual es conocida como la matriz de insumo producto.
48 
160 
A los elementos de la matriz A se les conoce por diversos nombres; coeficientes de insumo
producto, coeficientes de leontief o coeficientes técnicos.
Para conocer los niveles de producción que se requieren se despeja la matriz X
Por nuestro ejemplo
X  AX  D
IX  A X  D
IX  A X  D
Entonces
( I  A) X  D
I
1
X  ( I  A) D
1
X  ( I  A) D 
1
IA
0
1  70

29  50
 A
1

 60
0   200

1   100
 200
1  70

29  50
64 
160   0.7

48    0.5
160 
 0.4 

0.7 
40 

70 
40   70   251, 7 



70   60   265, 5 
Por lo tanto la industria A deberá producir 251,7 unidades y La industria B 265,5.
Profesor Eduardo Flores
Ejercicios.
1. Suponga que en una economía existen solo dos industrias, cuya interacción se resume
en la siguiente tabla
insumos de insumos de
la industria A la industria B
demandas
finales
producción
total
producción de la
industria A
240
750
210
1200
producción de la
industria B
720
450
330
1500
insumos
primarios
insumos totales
240
300
a) Obtenga la matriz de insumo producto
1

5
A
3

5
1 

2

3 

10 
b) Determine la matriz de producción si las demandas finales cambian a 312 unidades en
A y a 299 unidades en B
 I  A
1

 1
 
 0

1
0  5

1  3

5
1 

2

3 

10  
1

1  35

13  30
25 

40 
Por ende
1
 I  A  X  
1  35

13  30
25   312   1415 



40   299   1640 
c) ¿Cuáles son los nuevos insumos primarios correspondientes?
Bastara plantear la proporcionalidad
Para la industria A se necesitara
1415
1200
Y para la industria B se necesitara
 240  283 unidades
1640
1500
 300  328 unidades
Profesor Eduardo Flores
2. Suponga que en una economía existen solo dos industrias, cuya interacción se resume
en la siguiente tabla
insumos de insumos de
la industria A la industria B
demandas
finales
producción
total
producción de la
industria A
20
56
24
100
producción de la
industria B
50
8
22
80
insumos
primarios
insumos totales
30
16
a) Obtenga la matriz de insumo producto


A



7 

10

1 

10 
1
5
1
2
 I  A
1

 1
 
 0


0 

1 


1
5
1
2
7 

10

1 

10  
1

1  90

37  50
70 

80 
b) Si en cinco años las demandas finales cambian a 80 en el caso de la industria A y a
45 en el caso de la industria B. ¿Cuánto deberá producir cada industria para
satisfacer la demanda proyectada?
1
 I  A  X  
1  90

37  50
70   80   279.7297 



80   45   205.4054 
c) ¿Cuáles son los nuevos requerimientos de insumos primarios en cinco años para
las dos industrias?
279.7297
100
205.4054
80
 30  82.11891  83 Para la industria A
 16  41.0810  42
Para la industria B
Profesor Eduardo Flores
3. Suponga que en una economía existen solo dos industrias, cuya interacción se resume
en la siguiente tabla
Agricultura
Bienes
manufacturados
Mano de
obra
producción
total
Agricultura
200
200
100
500
Bienes
manufacturados
250
80
70
400
Mano de obra
60
90
insumos totales
a) Obtenga la matriz de insumo producto


A



1

2

1

5
2
5
1
2
 I  A
1

 1
 
 0


0 

1 


2
5
1
2
1 

2

1 

5  
1

1  80

23  50
50 

60 
b) Si en tres años la demanda de productos agrícolas decrece a 40 unidades y a 60
unidades para bienes manufacturados. Determine el nuevo vector de producción
que satisfaga estas nuevas demandas
 I  A
1
 X

1  80

23  50
50   40   269.5652 


 
60   60   243.4782 
c) ¿Cuáles son los nuevos requerimientos de mano de obra para cada sector?
269.5652
500
243.4782
400
 60  32.347  33 Para agricultura
 90  54.7828  55 Para bienes manufacturados
Profesor Eduardo Flores
4. La interacción entre dos sectores de una economía, está dada por la siguiente tabla
Industria P
Industria Q
Demandas
finales
600
750
650
2000
800
300
400
1500
600
450
Industria P
Industrias Q
demandas finales
insumos totales
producción
total
a) Obtenga la matriz de insumo producto
 3

10
A
 2

 5
1

2

1

5
 I  A
1

 1
 
 0

 3
0   10

1  2

 5
1 

2

1 

5  
1

1  40

18  20
25 

35 
b) Determine la matriz de producción si las demandas finales cambian a 1000 en el
caso de P y a 1700 en el caso de Q
1  40

18  20
25   1000   4583, 3333 


 
35   1700   4416.6666 
c) ¿Cuáles son los nuevos requerimientos de mano de obra?
4583, 3333
2000
4416.6666
1500
 600  1374.9999  1375 Para la industria P
 450  1324.9999  1325 Para la industria Q
Profesor Eduardo Flores
5. La interacción entre dos sectores de una economía hipotética, está dada por la
siguiente tabla
Industria P
Industrias Q
demandas finales
insumos totales
Industria P
Industria Q
Demandas
finales
producción
total
26
222
12
260
200
80
90
370
90
110
d) Obtenga la matriz de insumo producto
e) Determine la matriz de producción si las demandas finales cambian a 130 en el
caso de P y a 215 en el caso de Q
f) ¿Cuáles son los nuevos requerimientos de mano de obra?
6. Modelo insumo Producto: la interacción de las tres industrias P. Q y R está dada por la
tabla
industria
industria
P
Q
R
P
18
42
0
Q
0
40
80
R
40
90
40
insumos
primarios
35
75
25
Demandas producción
Finales
total
42
100
28
200
120
240
producción
total
a) Construya la matriz de insumo producto
b) Determine las nuevas producciones de P, Q y R si las demandas finales
cambian en el futuro a 65, 55 y 110, respectivamente.
c) ¿Cuáles serán entonces los insumos primarios para las tres industrias?
Profesor Eduardo Flores
7. Repita el ejercicio anterior para los partes sectores de economía dados en la tabla si las
nuevas demandas finales son 60, 50 y 20 para P, Q y R
industria
industria
P
Q
R
P
22
88
66
Q
80
40
60
R
76
38
57
insumos
primarios
40
20
20
Demandas producción
Finales
total
42
220
74
240
17
200
producción
total
8. Modelo insumo Producto: la interacción de las tres industrias P. Q y R está dada por la
tabla
industria
industria
P
Q
R
insumos en
mano de
obra
P
32
64
24
Q
60
30
150
R
40
80
80
16
60
120
Demandas producción
Finales
total
28
160
126
300
146
400
producción
total
a) Construya la matriz de insumo producto
b) Determine las nuevas producciones de P, Q y R si las demandas finales
cambian en el futuro a 25, 60 y 80, respectivamente. ¿Cuánto debería
producir cada industria para satisfacer esta demanda proyectada?
c) ¿Cuáles serán entonces los nuevos requerimientos de consumo en mano de
obra para las tres industrias?
Profesor Eduardo Flores
9. La interacción entre dos sectores de una economía hipotética, está dada por la
siguiente tabla
Industria P
Industrias Q
demandas finales
insumos totales
Industria P
Industria Q
Demandas
finales
producción
total
8
52
20
80
56
26
48
130
16
52
a) Obtenga la matriz de insumo producto
b) Si en tres años las demandas finales cambian a 58 en el caso de la industria A y a
79 en el caso de la industria B. ¿Cuánto deberá producir cada industria para
satisfacer la demanda proyectada?
c) ¿Cuáles serán entonces los nuevos requerimientos de consumo en mano de obra
para las tres industrias?
10. La interacción entre dos sectores de una economía hipotética, está dada por la
siguiente tabla
Industria P
Industrias Q
Insumos en mano
de obra
insumos totales
Industria P
Industria Q
Demandas
finales
producción
total
120
384
96
600
420
288
252
960
60
288
d) Obtenga la matriz de insumo producto
e) Si en tres años las demandas finales cambian a 140 en el caso de la industria A y a
287 en el caso de la industria B. ¿Cuánto deberá producir cada industria para
satisfacer la demanda proyectada?
f) ¿Cuáles serán entonces los nuevos requerimientos de consumo en mano de obra
para las tres industrias?
Soluciones y desarrollos en breve.
Atte, el profe
Profesor Eduardo Flores