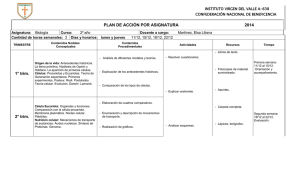
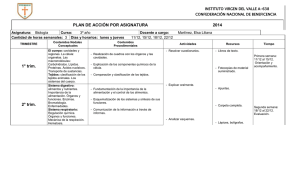
guia s1

Universidad Diego Portales
Facultad de Ingeniería
Gestión de Operaciones
1er semestre, 2011.
Carlos Melo R.
Guía Nº 1
Problema 1
En una empresa manufacturera la producción final de determinada semana fue de 30.000 unidades,
habiendo 20 trabajadores en la línea de producción que ganan $20 la hora normal, con un recargo del 50%
para las horas extra. La empresa trabaja 40 horas a la semana. Cada trabajador es capaz de producir 30
unidades en una hora. El costo por materiales de cada unidad producida es de $3. Los costos fijos por
arriendo del taller son de $6.000 por semana. El precio de venta neto de la unidades producidas es de $5.
Determine los costos totales de producción de la semana, los ingresos, y la productividad.
Solución:
Trabajadores
Horas semana
Req. Producción
Prod. Hombre
Horas semana
Prod. Horas normales
Prod. Horas extra
Horas extra
Salario
Pago salarios
Precio unitario
Costo unitario
Costo fijo
20
40
30000
30
800
24000
6000
200
20
22000
5
3
6000
Costos totales semana
Ingresos totales semana
Productividad
Problema 2
hb
hr
u/semana
u/HH
HH/semana
u/semana
u/semana
HH/semana
$/HH
$/semana
$/u
$/u
$/semana
118000
150000
1,271
Considere el problema de la p-mediana:
min
∑c
i , j∈N
ij
·d i · X ij
s.a:
∑X
j
= 1, ∀i ∈ N
ij
∑δ
j
=p
j
X ij ≤ δ j , ∀i, j ∈ N
X ij , δ j ∈ {0,1}, ∀i, j ∈ N
Explique el significado de cada restricción del modelo.
Solución:
•
•
•
•
La restricción 1 asegura que cada cliente es asignado a una planta.
La restricción 2 garantiza que se seleccionen exactamente p localizaciones para las plantas.
La restricción 3 asegura que los clientes se asignen a una planta solo si ésta ha sido
seleccionada
La restricción 4 especifica que todas las variables de decisión son binarias.
Problema 3
Resolviendo un problema de localización mediante Khumawala, usted ya ha resuelto la iteración de
minsave, y una iteración de maxsave. Como resultado de estas iteraciones, usted ya ha decidido abrir las
plantas 3 y 5, y cerrar la 4. Realice una iteración más del algoritmo. Especifique claramente qué plantas se
abren o se cierran en esta etapa, y si es necesario hacer otra iteración o no. Se entrega la matriz de costos, y
dos planillas de guía para que pueda hacer sus cálculos.
A
70
66
8
21
66
1
2
3
4
5
B
35
30
89
107
55
C
94
83
67
70
31
D
36
33
34
53
56
A
B
C
E
80
73
21
22
50
D
F
39
31
83
100
43
E
G
70
59
65
76
7
F
H
19
8
59
78
45
G
C. Fijo
42
64
46
80
38
H
Costo Tte. Actual
Iteración 2
1
2
3
4
5
A
B
C
D
E
F
G
H
C. Fijo MAXSAVE
Solución:
No es necesario calcular los maxsave de 3, 4 y 5, ya que se encuentran ya abiertas o cerradas.
A
8
Costo Tte. Actual
Iteración 2
1
2
3
4
5
A
0
0
B
20
25
B
55
C
0
0
C
31
D
0
1
D
34
E
0
0
E
21
F
4
12
F
43
G
0
0
H
26
37
G
7
H
45
C. Fijo MAXSAVE
42
8
64
11
Se debe abrir la planta 2. Para saber si se abre 1 o se cierra se debe hacer una nueva iteración.
Problema 4
Considere la siguiente serie de datos de demanda:
Período
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Trimestre
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Año
2000
2000
2000
2000
2001
2001
2001
2001
2002
2002
2002
2002
2003
2003
2003
2003
2004
2004
2004
2004
At
143,8
185,2
209,6
158,8
161,4
191,8
219,4
189,4
181,8
222,8
224,4
193,6
187,4
197,6
226,6
196,6
194,4
228
245,8
229,8
Realice un pronóstico de demanda para cada trimestre del año 2005 aplicando una regresión lineal con
estacionalidad.
Solución:
Agregamos la demanda a nivel anual:
Año
2000
2001
2002
2003
2004
Demanda Anual
697,40
762,00
822,60
808,20
898,00
Aplicando una regresión lineal, obtenemos la demanda para el año 2005:
Promedio
Suma
Año (x)
2000
2001
2002
2003
2004
2002
Demanda Anual (y)
697,40
762,00
822,60
808,20
898,00
797,64
x·y
1394800
1524762
1646845,2
1618824,6
1799592
7984823,8
x^2
4000000,00
4004001,00
4008004,00
4012009,00
4016016,00
4008006
20040030
Con esto, la demanda para el año 2005 sería de:
La demanda total por trimestre, y el factor estacional asociado a cada uno, son:
Trimestre
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Demanda Total
868,8
1025,4
1125,8
968,2
Sk
21,8%
25,7%
28,2%
24,3%
Con esto obtenemos la predicción para cada trimestre del 2005:
Período
21
22
23
24
Trimestre
Trim. 1
Trim. 2
Trim. 3
Trim. 4
Año
2005
2005
2005
2005
Pred. Año
931,9
931,9
931,9
931,9
Sk
21,78%
25,71%
28,23%
24,28%
Ft
203,00
239,59
263,05
226,22
Problema 5
1.
Considere que la demanda anual por un producto para el período 2000 – 2002 fue de 1.090, 910 y
890 unidades respectivamente. Estime la demanda del año 2003 aplicando suavizado exponencial
con ajuste de tendencia, con parámetros α = 0,25 y δ = 0,2. Considere que FIT 2000 = 0,95·A 2000 , y
que T 2000 = -20. Calcule el MAD de este ajuste para el año 2002, compárelo con el de un suavizado
exponencial sin tendencia con los mismos parámetros. Considere en ambos casos al año 2000
dentro del cálculo del MAD.
Solución:
Período
2000
2001
2002
2003
At
1090
910
890
Ft
1049
1001
956
Tt
-20.00
-17.28
-23.37
-27.77
FITt
1036
1032
978
928
Ft (S/A)
1090
1090
1045
1006
MAD
ErrorAbs1
55
122
88
ErrorAbs2
0
180
155
88
112
El suavizado con tendencia tiene un MAD de 88, menor (y por lo tanto mejor) que el del caso sin tendencia
que es de 112.
2.
Suponga que usted cuenta con un programa que resuelve el problema de la p-mediana en su forma
convencional, donde todos los nodos son puntos de demanda y candidatos a localización a la vez.
Sin modificar el código del programa, explique cómo podría utilizar esta herramienta para resolver
una instancia en la que existen dos conjuntos de nodos: uno que corresponde a puntos de
demanda, pero no que no sirven para localizarse, y otro conjunto que contiene nodos que son
potenciales ubicaciones pero no son puntos de demanda.
Solución:
A los nodos de localización sin demanda se les asigna demanda cero, y a los nodos de demanda que no son
de localización se les pone un costo fijo lo suficientemente alto como para que nunca sean utilizados.
Problema 6
1.
Considere que se conocen los costos de operación para cuatro candidatos a localización de plantas
respecto a cuatro puntos de demanda a atender, y los costos fijos de cada candidato a localización,
como se indica en la tabla. Determine cuáles plantas abrir utilizando la heurística de Khumawala.
Indique claramente qué planta atiende a qué punto de demanda, y los costos totales de la solución
encontrada.
A
9
74
46
99
33
1
2
3
4
5
B
34
89
18
74
55
C
77
66
70
64
77
D
74
82
63
73
100
C. Fijo
50
30
40
30
10
Solución:
MINSAVE:
1
2
3
4
5
A
24
0
0
0
0
B
0
0
16
0
0
C
0
0
0
2
0
D
0
0
10
0
0
Costo Tte. Actual
33
55
77
100
MAXSAVE 1:
1
2
3
4
5
A
24
0
0
0
B
21
0
37
0
C
0
11
7
13
D
26
18
37
27
Costo Tte. Actual
33
18
70
63
MAXSAVE 2:
1
2
3
4
5
A
24
B
0
C
0
D
0
0
0
6
0
Costo Tte. Actual
33
18
70
63
C. Fijo
50
30
40
30
10
MINSAVE
-26
-30
-14
-28
-10
ESTADO
0
0
0
0
1
C. Total:
275
MAXSAVE
21
-1
41
10
ESTADO
0
-1
1
0
1
C. Total:
234
C. Fijo
50
MAXSAVE
-26
30
-24
ESTADO
-1
-1
1
-1
1
C. Fijo
50
30
40
30
C. Total:
234
Resumen:
Costos variables:
Punto de Demanda
Atendido Desde
Costo Variable
A
5
33
B
3
18
C
3
70
D
3
63
Total:
184.00
3
Sí
40
4
No
0
Total:
50.00
Total:
234.00
Costos Fijos:
Planta
Utilizada?
Costo Fijo
Costos Totales:
2.
1
No
0
2
No
0
¿Qué corresponde hacer según la heurística de Khumawala en las siguientes situaciones?
a.
b.
c.
d.
e.
Al resolver MINSAVE se obtiene que todas las plantas tienen MINSAVE negativo.
Al resolver MINSAVE se obtiene que dos plantas tienen MINSAVE positivo, una cero, y el
resto negativo.
Al resolver MAXSAVE se obtiene que de las plantas pendientes todas tienen MAXSAVE
negativo excepto una que tiene MAXSAVE igual a cero.
Al resolver MAXSAVE se obtiene que de las plantas pendientes todas tienen MAXSAVE
positivo excepto una que tiene MAXSAVE igual a cero.
Al resolver MAXSAVE se obtiene que dos plantas tienen MAXSAVE negativo, una cero, y las
otras tres positivo.
Solución:
a.
b.
c.
d.
e.
Se abre la menos negativa (si hay empate se escoge una en forma arbitraria), y las demás
permanecen pendientes.
Se deben abrir todas las positivas. La con MINSAVE cero puede abrirse o permanecer pendiente,
pero dado que el ahorro mínimo asegurado es cero, resulta razonable abrirla para que haya menos
iteraciones. Las de MINSAVE negativo permanecen pendientes.
Se cierran todas las con MAXSAVE negativo. La otra se puede abrir o cerrar, da lo mismo porque el
costo total será el mismo.
Se debe abrir la de mayor MAXSAVE. La de MAXSAVE cero se puede dejar pendiente o cerrar, pero
como su ahorro máximo es cero, podemos cerrarla inmediatamente sabiendo que no se pierde
nada. Las demás plantas permanecen pendientes.
Se debe abrir la de mayor MAXSAVE. La de MAXSAVE cero se puede dejar pendiente o cerrar, pero
como su ahorro máximo es cero, podemos cerrarla inmediatamente sabiendo que no se pierde
nada. Las plantas con MAXSAVE negativo se cierran. Las plantas positivas que no se abrieron
permanecen pendientes.
Problema 7
Considere el siguiente problema de transporte:
Source 1
Source 2
Source 3
DEMAND
Destination 1
10
8
12
80
Destination 2
8
12
10
120
Destination 3
0
0
0
60
SUPPLY
60
80
120
La destinación 3 corresponde a un nodo ficticio para el balanceo. Encuentre la solución óptima, comenzando
con la solución cuyas variables básicas son X12, X13, X21, X22, y X32.
Solución:
Destination 1
Destination 2
Destination 3
Iteration 1
Source 1
Source 2
Source 3
(6)
80
(6)
(0)
(0)
120
60
(-4)
(-2)
Iteration 2
Source 1
Source 2
Source 3
(2)
80
(2)
(0)
(4)
120
60
(0)
(-2)
Iteration 3
Source 1
Source 2
Source 3
(4)
80
(4)
60
(2)
60
(2)
(0)
60
Los envíos y los costos de la solución óptima son:
From
To
Shipment
Cost per unit
Shipment cost
Source 1
Source 2
Source 2
Source 3
Source 3
Destination 2
Destination 1
Destination 3
Destination 2
Destination 3
60
80
0
60
60
8
8
0
10
0
480
640
0
600
0
El costo total es de 1.720.
Problema 8
Una empresa produce motos en dos plantas, una en China y otra en Brasil. La producción máxima factible en
cada planta (en miles de unidades mensuales) son, respectivamente, 50 y 30. La empresa cuenta con tres
centros de distribución (América, Asia, y Europa) con demandas mensuales de 20, 10 y 30, respectivamente.
Las utilidades reportadas por atender cada punto de demanda (por cada mil unidades de demanda) desde
cada centro de distribución se entregan en la tabla a continuación:
China
Brasil
Demanda
América
10
12
20
Asia
24
20
10
Europa
15
12
30
Oferta
50
30
Determine el esquema de distribución óptimo para la empresa. Convierta el problema a minimización
aplicando la regla del máximo, y utilice la solución inicial que se obtiene con el método de la esquina
noroeste. Para el balanceo considere utilidades nulas en los orígenes o destinos ficticios. Indique las
utilidades totales mensuales de la solución propuesta.
Solución:
Convertimos a minimización, agregando un destino ficticio para capturar el exceso de demanda:
China
Brasil
Demanda
América
14
12
20
Asia
0
4
10
Europa
9
12
30
Ficticio
0
0
20
Oferta
50
30
Las iteraciones se muestran a continuación (los números entre paréntesis representan costos reducidos):
América
Asia
Europa
Ficticio
It. 1
China
Brasil
20
(-5)
10
(1)
20
10
(3)
20
It. 2
China
Brasil
10
10
10
(6)
30
(5)
(-2)
20
It. 3
China
Brasil
(2)
20
10
(4)
30
(3)
10
10
Conviene enviar desde China 10 a Asia, 30 a Europa, y dejar 10 sin enviar, con utilidad de 10*24 + 30*15 =
690, y enviar desde Brasil 20 a América, dejando 10 sin enviar, con una utilidad de 20*12 = 240. La utilidad
total es de 930.
Problema 9
Una empresa cuenta con dos bodegas, una ubicada en Pudahuel y otra en Lo Espejo, para atender la
demanda existente en tres centros comerciales de la capital. Los tres centros corresponden a los sectores
Norte, Sur y Cordillera, y consumen respectivamente 200, 100 y 350 unidades mensuales. La capacidad
máxima de cada bodega es de 300 y 400 unidades mensuales, respectivamente. Los costos unitarios de
distribución se detallan a continuación:
Pudahuel
Lo Espejo
Norte
18
25
Sur
22
20
Cordillera
39
34
La empresa desea determinar cuánto enviar desde cada bodega hasta cada centro comercial de forma de
minimizar sus costos de distribución.
3.
Plantee este problema como un problema de programación lineal.
Solución:
s.a:
La sexta restricción es opcional (se puede derivar de las demás).
También se puede escribir sin usar variables de holgura, cambiando las restricciones por:
4.
(doble) Resuelva este problema aplicando el algoritmo estudiado en clases. Utilice el método de la
esquina noroeste para obtener la solución inicial, usando costos nulos para el nodo ficticio. Indique
las cantidades óptimas enviadas y los costos totales de distribución.
Solución:
Norte
Sur
Cordillera
Destination 4
Iteration 1
Pudahuel
Lo Espejo
200
12
100
3
0
350
-5
50
Iteration 2
Pudahuel
Lo Espejo
200
3
100
-2
5
350
0
50
Iteration 3
Pudahuel
Lo Espejo
200
9
50
50
3
350
50
2
Partiendo de la otra solución inicial se llega al mismo resultado:
Op. 1
Iteration 1
Pudahuel
Lo Espejo
Iteration 2
Pudahuel
Lo Espejo
Norte
Sur
Cordillera
Destination 4
200
9
100
0
3
350
-2
50
200
9
50
50
3
350
50
2