Anexo 1.2: Modelación Matemática de Sistemas Físicos

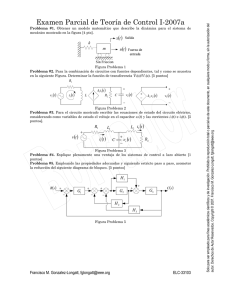
ELC-33103
Teoría de Control
Anexo 1.2
Modelación Matemática de
Sistemas Físicos
Prof. Francisco M. Gonzalez-Longatt
[email protected]
http://www.giaelec.org/fglongatt/TeoriaControlI.html
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• Obtener un modelo dinámico para el sistema de
fuerzas trasnacional en al dirección vertical que se
muestra considerando que la entrada fuerza f(t),
Salidas x1(t) x2(t)
B/2
k2
B/2
x2 (t )
M2
k1
x1 (t )
M1
f (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
B/2
k2
B/2
x2 (t )
M2
Salida 2
x1 (t ) − x2 (t )
Elongación
k1
x1 (t )
M1
f (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Salida 1
Entrada 1
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• Con las posiciones de referencia determinadas tal
como se ha especificado.
• Un desplazamiento inicial del resorte superior
produce una fuerza igual
p
g y opuesta
p
a M1g + M2gg.
• Y un desplazamiento inicial del resorte inferior
produce una fuerza que compensa M1g.
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• Se efectúa un diagrama de cuerpo libre:
FB2 =
B dx2 (t )
FR2 = K2 x2 (t )
2 dt
FB1 =
B dx2 (t )
2 dt
M2
FR1 = K1[x1(t ) − x2 (t )]
Fuerzas Pasivas se dirigen
en sentido opuesto al
desplazamiento
x2 (t )
FR1 = K1[x1(t ) − x2 (t )]
x1 (t )
M1
f (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• Del cuerpo M1 se tiene:
FR1 = K1[x1(t ) − x2 (t )]
Aplicando la 2da Ley de
Newton:
f (t ) = M 1a1 + FR1
x1 (t )
M1
f (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Sustituyendo las respectivas fuerzas se
tiene:
d 2 x1 (t )
f (t ) = M 1
+ K1 [x1 (t ) − x2 (t )]
2
dt
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• Del cuerpo M2 se tiene:
FB2 =
B dx2 (t )
FR2 = K2 x2 (t )
2 dt
FB1 =
B dx2 (t )
2 dt
M2
x2 (t )
A li d la
Aplicando
l 2da
2d Ley
L de
d Newton:
N t
0 = M 2 a2 + FR 2 + FB1 + FB 2 − FR1
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
FR1 = K1[x1(t ) − x2 (t )]
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
FB2 =
B dx2 (t )
FR2 = K2 x2 (t )
2 dt
FB1 =
B dx2 (t )
2 dt
M2
Sustituyendo las respectivas fuerzas se
tiene:
x2 (t )
FR1 = K1[x1(t ) − x2 (t )]
d x2 (t )
dx(t )
0 = M2
− K1 [x1 (t ) − x2 (t )] + K 2 x2 (t ) + B
2
dt
dt
2
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
1. Modelo Matemático de Sistemas Físicos
• El modelo dinámico del sistema queda dado por las
siguientes ecuaciones diferenciales:
d x2 (t )
dx(t )
− K1 [x1 (t ) − x2 (t )] + K 2 x2 (t ) + B
=0
M2
2
dt
dt
2
d 2 x1 (t )
M1
+ K1 [x1 (t ) − x2 (t )] = f (t )
2
dt
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
2. Función de Transferencia
• Para la combinación de circuitos con fuentes
dependientes, tal y como se muestra en la siguiente
Figura.
R1
v1 (t )
i1 (t )
L
k1i1 (t )
R2
+
+
v2 (t )
C
+
−
k 2 v2 (t )
v3 (t )
−
• Determinar la función de transferencia V3(s)/V1(s).
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
−
2. Función de Transferencia
• Se procede a establecer las ecuaciones circuitales que
definen la mala de la entrada
R1
v1 (t )
i1 (t )
L
k1i1 (t )
R2
+
+
v2 (t )
C
+
−
k 2 v2 (t )
v3 (t )
−
di1 (t )
vin (t ) = R1i (t ) + L
dt
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
−
2. Función de Transferencia
• En la segunda red acoplada, y se aplica la ley de
dv2 (t )
corriente de Kirchoff:
ic (t ) = C2
R
dt
1
v1 (t )
i1 (t )
k1i1 (t )
R2
L
+
+
v2 (t )
C
+
−
k 2 v2 (t )
v3 (t )
−
k 1i1 (t )
ic (t )
v2 (t )
R2
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
v2 (t )
dv2 (t )
k1i1 (t ) =
+ C2
R2
dt
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
−
2. Función de Transferencia
• De la tercera malla se tiene:
R1
v1 (t )
i1 (t )
L
k1i1 (t )
R2
+
+
v2 (t )
C
+
−
k 2 v2 (t )
v3 (t )
−
vout (t ) = k 2 v2 (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
−
2. Función de Transferencia
• El modelo dinámico del circuito resulta ser:
v2 (t )
dv2 (t )
k1i1 (t ) =
+ C2
R2
dt
vout (t ) = k 2 v2 (t )
di1 (t )
vin (t ) = R1i (t ) + L
dt
• Se procede a aplicar transformada de Laplace en
ambos lados de cada ecuación,
ecuación considerando las
condiciones iníciales nulas.
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
2. Función de Transferencia
• Aplicando transformada de Laplace resulta:
di1 (t )
vin (t ) = R1i (t ) + L
dt
v2 (t )
dv2 (t )
k1i1 (t ) =
+ C2
R2
dt
vout (t ) = k 2 v2 (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Vin (s ) = R1 I1 (s ) + sLI1 (s )
V2 (s )
k1 I1 (s ) =
+ sC2V2 (s )
R2
Vout (s ) = k 2V2 (s )
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
2. Función de Transferencia
• Se despeja I1:
Vin (s )
I1 (s ) =
R1 + sL
V2 (s )
k1 I1 (s ) =
+ sC2V2 (s )
R2
⎡1
⎤
Vin (s )
= V2 (s )⎢ + sC2 ⎥
k1
R1 + sL
⎦
⎣ R2
• Se opera matemáticamente:
Vout
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
k 2 R2 k1Vin (s )
=
(R1 + sL )(1 + sR2C2 )
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
2. Función de Transferencia
• Finalmente la función de transferencia resulta:
Vout
k 2 R2 k1
=
Vin (R1 + sL )(1 + sR2C2 )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Para el sistema de control mostrado en la Figura.
TW (s )
Θ R (s )
+
−
Θ E (s )
100
K0
Va (s ) +
−
I a (s )
1
sLa + Ra
KT
N1
N2
++
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Θ y (s )
Kb
1.0
• Determine
D
i la
l representación
ió en ecuación
ió de
d estado
d
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Para determinar la representación de estado del
sistema se tiene que la entrada θ R (t ) y salida θ y (t ) .
• Para las variables intermedias se tiene:
−1
va (t ) = L {Va (s )}
ia (t ) = L {I a (s )}
ωm (t ) = L {Ω M (s )}
ω y (t ) = L {Ω y (s )}
−1
−1
−1
θ c (t ) = L {Θ c (s )}
Θ R (s )
+
−
−1
TW (s )
Θ E (s )
N1
N2
++
100
K0
Va (s ) +
−
I a (s )
1
sLa + Ra
KT
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Θ y (s )
Kb
1.0
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Tomando en cuenta esta sección del diagrama de
()
bloques:
TW s
Θ R (s )
Va (s ) +
−
+
Θ E (s )
−
I a (s )
1
sLa + Ra
Kb
100
K0
Va (s ) +
−
I a (s )
1
sLa + Ra
KT
N1
N2
++
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Kb
1 .0
KT
Ω M (s )
dia
+ Ra ia + K bωm (t )
va (t ) = La
dt
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
Θ y (s )
3. Función de Transferencia
• Para otra porción del sistema resulta:
TW (s )
TW (s )
Θ R (s )
KT Ia (s)
N1
N2
++
+
−
Θ E (s )
100
K0
Va (s ) +
−
I a (s )
1
sLa + Ra
KT
N1
N2
++
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Kb
1.0
Ω M (s )
1
sJ eq + Beq
dω m
N1
K T ia (t ) +
TW (t ) = J EQ
+ BEQωm
N2
dt
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
Θ y (s )
3. Función de Transferencia
• Para la parte de la entrada se tiene:
TW (s )
Θ R (s )
+
−
Θ E (s )
100
K0
Va (s ) +
−
N1
N2
++
I a (s )
1
sLa + Ra
KT
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Θ y (s )
Kb
1 .0
Θ R (s )
+
Θ E (s )
−
100
Θ y (s )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
K0
Va (s )
[
]
va (t ) = 100 K 0 θ r (t ) − θ y (t )
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Para la parte de la salida:
Θ R (s )
TW (s )
+
−
Θ E (s )
100
K0
Va (s ) +
−
I a (s )
1
sLa + Ra
KT
N1
N2
++
Ω M (s ) N1 Ω y (s ) 1
1
sJ eq + Beq
N2
s
Kb
Ω M (s ) N1 Ω y (s ) 1
N2
s
1.0
Θ y (s )
N 1 dθ y
ωm (t ) =
N 2 dt
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
Θ y (s )
3. Función de Transferencia
• Finalmente el conjunto de ecuaciones que definen la
dinámica son:
dia
va (t ) = La
+ Ra ia + K bωm (t )
dt
dω m
N1
TW (t ) = J EQ
+ BEQωm
K T ia (t ) +
N2
dt
N 1 dθ y
ωm (t ) =
N 2 dt
d
[
]
va (t ) = 100 K 0 θ r (t ) − θ y (t )
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Se construye la presentación de modelo de estado:
⎡ Ra
⎢− L
⎡ i&a ⎤ ⎢ a
⎢ ⎥ ⎢ KT
⎢ω& m ⎥ = ⎢ J
⎢ θ&y ⎥ ⎢ EQ
⎣ ⎦
⎢ 0
⎣⎢
kb
−
La
BEQ
−
J EQ
N1
N2
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
100ko ⎤
⎡100ko
−
⎥
La ⎥ ⎡ i ⎤ ⎢ La
a
⎢
⎢ ⎥ ⎢
⎥
0 ⎥ ⎢ωm ⎥ +
0
⎢
⎥ ⎢⎣ θ y ⎥⎦ ⎢
0
⎥
⎢
0
⎥⎦
⎣
⎤
0 ⎥
⎥ θ
N1 ⎥ ⎡ r ⎤
N 2 J EQ ⎥ ⎢⎣TW ⎥⎦
0 ⎥
⎥
⎦
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
3. Función de Transferencia
• Las ecuaciones algebraicas resultan ser:
⎡θ e ⎤ ⎡0
⎢θ ⎥ = ⎢0
⎣ y ⎦ ⎢⎣
0
N1
N2
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
⎡
⎤
i
a
− 1⎤
⎡1 0⎤ ⎡ θ r ⎤
⎢
⎥
⎥ ⎢ωm ⎥ + ⎢
⎢
⎥
⎥
0⎥
0 0⎦ ⎣TW ⎦
⎣
⎦ ⎢⎣ θ y ⎥⎦
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
4. Reducción de Diagrama de Bloques
• Determine el diagrama de bloque equivalente
reducido del siguiente sistema.
1
s
Θ R (s )
+
−
1
1 + 100s
+
−
1
s+5
1
− +
55s + 5
100s + 1
100s 2 + 10s + 1000
1 +
s+5
−
Θ y (s )
−105
1.0
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
4. Reducción de Diagrama de Bloques
• Se modifica la posición de un punto de bifurcación.
100s 2 + 10 s + 100
100 s + 1
1
s
Θ R (s )
+
1
1 + 100s
−
+
1
− +
55s + 5
−
100s + 1
100s 2 + 10s + 1000
1
s+5
1 +
s+5
−
−105
1.0
• S
Se modifica
difi la
l posición
i ió de
d un punto
t de
d bifurcación,
bif
ió y
se efectúa una simplificación de cascada.
100 s 2 + 10 s + 100
(100s + 1)(s + 5)
1
s
Θ R (s )
+
−
1
1 + 100s
+
−
1
− +
55s + 5
−105
1
s+5
+
−
Θ y (s )
100s + 1
100s + 10 s + 1000
2
1 .0
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
Θ y (s )
4. Reducción de Diagrama de Bloques
• Se simplifica otra cascada.
100 s 2 + 10 s + 100
(100s + 1)(s + 5)
1
s
+
Θ R (s )
−
+
1
1 + 100 s
1
− +
55s + 5
− 105(100s + 1)
−
1
s+5
+
−
Θ y (s )
100s 2 + 10 s + 1000
1 .0
• Se
S simplifica
i lifi la
l sumatoria
t i
1
s
Θ R (s )
+
−
1
1 + 100 s
+
−
1
− +
55s + 5
− 105(100s + 1)
1 ⎡ 100s 2 + 10s + 100 ⎤
1−
(s + 5) ⎢⎢⎣
(100s + 1) ⎥⎥⎦
Θ y (s )
100s 2 + 10s + 1000
1 .0
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008
4. Reducción de Diagrama de Bloques
• Afectando sumas y simplificando:
1
s
Θ R (s )
+
+
1
1 + 100 s
−
1
− +
55s + 5
− 105(100s + 1)
−
− 100s 2 − 90 s + 999
(s + 5)(100s + 1)
Θ y (s )
100s 2 + 10s + 1000
1.0
• Finalmente
Fi l
t resulta:
lt
Θ R (s )
(− 20s
2
)(
)(
)
− 2s − 200 554s + 5500s 2 + 5 100s 2 − 90s + 999
11000000s + 45520000s + 146339100s 442042430s + 90179752s − 1089947161s 2 − 110608085s − 999000
7
6
TEORÍA DE CONTROL
Ejemplos de Modelación de Sistemas Físicos
5
4
3
Θ y (s )
Dr. Francisco M. Gonzalez-Longatt, [email protected]
Copyright © 2008