Consumo medio por familia

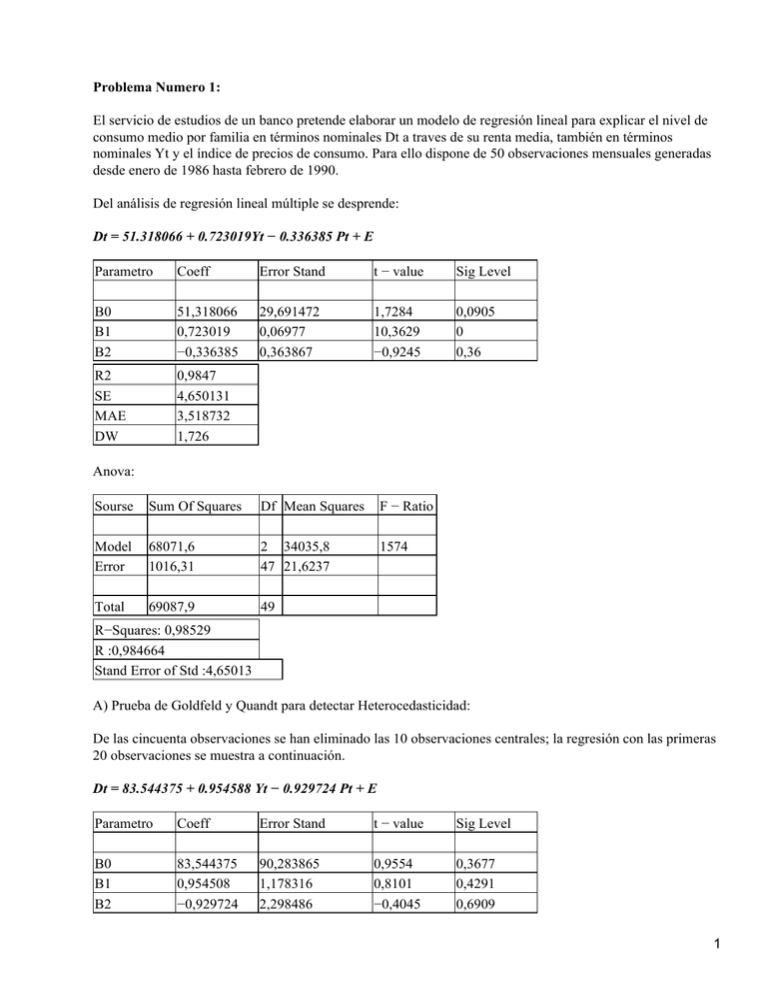
Problema Numero 1:
El servicio de estudios de un banco pretende elaborar un modelo de regresión lineal para explicar el nivel de
consumo medio por familia en términos nominales Dt a traves de su renta media, también en términos
nominales Yt y el índice de precios de consumo. Para ello dispone de 50 observaciones mensuales generadas
desde enero de 1986 hasta febrero de 1990.
Del análisis de regresión lineal múltiple se desprende:
Dt = 51.318066 + 0.723019Yt − 0.336385 Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
51,318066
0,723019
−0,336385
29,691472
0,06977
0,363867
1,7284
10,3629
−0,9245
0,0905
0
0,36
R2
SE
MAE
DW
0,9847
4,650131
3,518732
1,726
Anova:
Sourse
Sum Of Squares
Df Mean Squares
F − Ratio
Model
Error
68071,6
1016,31
2 34035,8
47 21,6237
1574
Total
69087,9
49
R−Squares: 0,98529
R :0,984664
Stand Error of Std :4,65013
A) Prueba de Goldfeld y Quandt para detectar Heterocedasticidad:
De las cincuenta observaciones se han eliminado las 10 observaciones centrales; la regresión con las primeras
20 observaciones se muestra a continuación.
Dt = 83.544375 + 0.954588 Yt − 0.929724 Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
83,544375
0,954508
−0,929724
90,283865
1,178316
2,298486
0,9554
0,8101
−0,4045
0,3677
0,4291
0,6909
1
R
SE
MAE
DW
0,3931
2,998114
2,551865
2,464
Anova:
Sourse
Sum of Squares
Df Mean Squares
F− Ratio
Model
Error
128,578
152,808
2 64,289
17 8,98868
7,15222
Total
281,386
19
R: 0,456946
R Adj: 0,393057
Stand Error of Est :2,99811
Dw: 2,46431
Para las veinte siguientes observaciones los resultados de la regresión y la ANOVA son los siguientes:
Dt = 23.583192 + 0.569763Yt + 0.183243 Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
23,583192
0,569763
0,183243
235,527171
0,404417
2,617527
0,1001
1,4089
0,07
0,9214
0,1769
0,945
R
SE
MAE
DW
0,9282
5,507667
4,222239
2,017
Anova:
Sourse
Sum of Squares
Df Mean Squares
F− Ratio
Model
Error
7520,07
515,685
2 3760,04
17 30,3344
123,953
Total
8035,76
19
R: 0,935826
R Adj: 0,928276
Stand Error of Est :5,50767
Dw: 2,01651
2
H0: Homocedasticidad
H1: Heterocedasticidad
Golfeld−Guandt SRC2
SRC1
= 8035,76
281,386
= 28,5577818
F obs: 28,5577818
F tabla (0.025 , 20 , 20) = 2,4645
Por lo tanto se rechaza H0 y se acepta H1, es decir hay indicios de heterocedasticidad en el modelo bajo esta
prueba.
b) Pruebas de Park para detectar Heterocedasticidad.
ln e2 = 0.63872 + 0.833311ln Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
−5,670144
1,440697
4,684303
0,90826
−1,2079
1,5862
0,2330
0,1193
R
SE
MAE
DW
0,0300
1,895700
1,551507
2,391
H0:Homocedasticidad
H1:Heterocedasticidad.
T obs: 1,5862
T tabla: (0.025, 48) = 2.0106
Se acepta H0, y se rechaza H1; es decir existe homocedasticidad por el lado de la variable renta mensual
media
ln e2 = −7.57908 + 2.63667 ln Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
−17,19214
3,9928
13,941338
2,935982
−1,2322
1,3600
0,2235
0,1802
R
SE
MAE
DW
0,0170
1,908333
1,570581
2,373
3
H0: Homocedasticidad
H1:Heterocedasticidad
T obs:1,3600
T tabla:2,0106
Se acepta H0 y se rechaza H1; es decir el modelo es homocedastico por el lado de la variable Indice de
Precios.
c) Prueba de Rango de Spearman para detectar Heterocedasticidad.
Dt = 51,318066+ 0,723019 Yt − 0,336385 Pt + E
A) Dt = 51,318066+0,723019 Yt + E
Rs= 1 − 6 16126 = 0,22564225603
50 (502 −1)
t= (0,22564225603) raiz (50−2) = 1,60467972818
raiz 1− 0,225642256032
H0: Homocedasticidad
H1: Heterocedasticidad
T tabla (0,05; 50−2) = 1,6772
Dado que t no pertenece a la région de rechazo se puede decir que no existe heterocedasticidad en esta sub
regresión.
B) Dt = 51,318066 − 0,336385 Pt + E
Rs= 1 − 6 15366 = 0,262136854742
50 (502 −1)
t= (0,262136854742) raiz (50−2) = 1,88194778341
raiz 1− 0,2621368547422
H0: Homocedasticidad
H1: Heterocedasticidad
T tabla (0,05; 50−2) = 1,6772
Como t pertenece a la región de rechazo se puede afirmar que el modelo presenta problemas de
Heterocedasticidad por parte de la variable Pt.
4
d) Compara los Resultados Obtenidos.
Tomando en consideración las tres pruebas realizadas para la determinación de Heterocedasticidad en el
modelo presentado, se concluye que el modelo si tiene problemas de Heterocedasticidad; reflejado tanto en la
prueba de Goldfeld y Quandt, como en la prueba de rango de Speraman, la que dice que la variable que
presenta heterocedasticidad es la Pt.
En la prueba de Park, no se refleja muestras de Heterocedasticidad; lo que demuestra que no es totalmente
concluyente.
e) Prueba de D − W para Autocorrelación Serial
Del análisis de regresión lineal se desprenden los siguientes resultados bajo MCO
Dt = 51.318066 + 0.723019Yt − 0.336385 Pt + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
51,318066
0,723019
−0,336385
29,691472
0,06977
0,363867
1,7284
10,3629
−0,9245
0,0905
0
0,36
R2
SE
MAE
DW
0,9847
4,650131
3,518732
1,726
Un supuesto importante en el modelo de regresión lineal es que no hay correlación serial o autocorrelación
entre las perturbaciones ui consideradas dentro de la función de regresión poblacional.
Para detectar la no existencia de este supuesto se utilizara la prueba del estadístico d, de Durbin y Watson, el
cual define como la razón de la suma de las diferencias al cuadrado de residuales sucesivos sobre la suma
residuo cuadrado, considerando la siguiente formula.
D = Sumatoria ( ui − ui − 1) 2
Sumatoria ui2
1,726
0 dl dv 2 4−dv 4−dl 4
1.462 1.628 2.372 2.538
Como en la grafica se muestra, los valores dl y dv, son sacados de una tabla que esta expresada en un grado de
0.05 es decir 5% de significancia, con 50 observaciones y 2 variables, esto demuestra la no existencia de
autocorrelación serial; es decir no hay correlación serial o autocorrelación entre las perturbaciones ui
consideradas dentro de la función de regresión poblacional.
f) Corrección del Modelo:
5
Como se pudo ver, a travez de la prueba de Rango de Spearman; la variable que produce heterocedasticidad
en el modelo es la variable Pt; la cual mide el Indice de Precio; considerando lo anterior se procedió a la
corrección del modelo dividiendo las variable del mismo por la variable que presenta el problema, de esta
forma:
Dt/Pt = B0 + B1 Yt/Pt − B2 Pt/Pt.
El nuevo Análisis de Regresión y Anova se presentan a continuación.
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
1,325496
0,589614
0,0588308
0,0325602
6,40352
18,1084
0,0000
0,0000
R2
SE
MAE
DW
0,933976
Sourse
Sum of Squares
Df Mean Squares
F− Ratio
Model
Error
1.77404
0.259683
1 1,77404
48 0,005410
327,9150
Total
2,033725
49
R: 0,933976
R Adj: 0,8723
Stand Error of Est :0,0735531
Dw:
Problema 2:
El numero total de calefactores vendidos por una empresa Ft, depende del numero de puntos de distribución
Pt, que dicha empresa tiene y de la temperatura media del área en la que la misma trabaja Et.
Del análisis de regresión se desprende:
Ft = 2,353547 + 0,473013 Pt + 0,487835 Et + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
2,353547
0,473013
0,487835
0,531831
0,023849
0,108628
4,4254
19,8336
4,4909
0,001
0,0000
0,0000
R2
SE
MAE
0,8949
1,224324
0,951351
6
DW
1,763
Anova:
Sourse
Sum Of Squares
Df Mean Squares
F − Ratio
Model
Error
615,375
68,9525
2 307,687
46 1,49897
205,266
Total
684,327
48
R−Squares: 0,89924
R :0,89486
Stand Error of Std :1,22432
a) Prueba de Goldfeld y Quandt para detectar Heterocedasticidad:
De las cuarenta y nueve observaciones se han eliminado las 19 observaciones centrales; la regresión con las
primeras 15 observaciones se muestra a continuación.
Ft = 4,716992 + 0,223534 Pt + 0,457795 Et + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
4,716992
0,223534
0,457795
3,087425
0,252182
0,267562
1,5278
0.8864
1,7110
0,1525
0,8864
0,1128
R
SE
MAE
DW
0,1405
1,394835
1,082134
1,460
Anova:
Sourse
Sum of Squares
Df Mean Squares
F− Ratio
Model
Error
8,34545
23,3468
2 4,17273
12 1,94557
2,14474
Total
31,6922
14
R: 0,263328
R Adj: 0,140549
Stand Error of Est :1,39484
Dw: 1,45961
Para las quince siguientes observaciones los resultados de la regresión y la ANOVA son los siguientes:
7
Ft = −7,003447 + 0,729608 Pt + −0,729302 Et + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
−7,003447
0,729608
−0,729302
2,393968
0,07039
0,296125
−2,9255
10,3652
−2,4628
0,0127
0,0000
0,0299
R
SE
MAE
DW
0,9071
0,651768
0,404418
2,182
Anova:
Sourse
Sum of Squares
Df Mean Squares
F− Ratio
Model
Error
58,9484
5,09761
2 29,4742
12 0,424801
69,3836
Total
69,0460
14
R: 0,950407
R Adj: 0,907172
Stand Error of Est :0,651768
Dw: 2,18177
H0: Homocedasticidad
H1: Heterocedasticidad
Golfeld−Guandt SRC2
SRC1
= 69,0480
31,6922
= 2,17870643
F obs: 2,17870643
F tabla (0.025 , 15 , 15) = 2,8621
Por lo tanto se rechaza H0 y se acepta H1, es decir hay indicios de heterocedasticidad en el modelo bajo esta
prueba.
b) Pruebas de Park para detectar Heterocedasticidad.
Dado los datos en donde la variable temperatura media, esta expresada en forma negativa es imposible
determinar el Logaritmo de esta variable necesario para la determinación de la prueba, con lo que se concluye
que las condiciones necesarias para la determinación de Heterocedasticidad bajo esta prueba no están dada.
c) Prueba de rango de Spearman para detectar Heterocedasticidad:
8
.
Ft = 2,353547+ 0,473013 Pt + 0,487835 + E
A) F t = 2,353547 + 0,473013 Pt + E
Rs= 1 − 6 19896 = 0,0140816326531
49 (492 −1)
t= (0,0140816326531) raiz (49−2) = 0,0965483825285
raiz 1− 0.0148163265312
H0: Homocedasticidad
H1: Heterocedasticidad
T tabla (0,05; 49−2) = 1,6779
Como t; no pertenece a la región de rechazo se puede decir que no existe evidencia suficiente como para
demostrar que el modelo tiene Heterocedasticidad, por parte de la variable Pt.
B) F t= 2,353547 + 0,487835 Et + E
Rs= 1 − 6 25338 = 0,292755102041
49 (492 −1)
t= (0,292755102041) raiz (49−2) = 2,09898995261
raiz 1− 0,2927551020412
H0: Homocedasticidad
H1: Heterocedasticidad
T tabla (0,05; 49−2) = 1,6779
Considerando que t pertenece a la región de rechazo se puede decir que existe Heterocedasticidad por parte de
la variable Et bajo esta prueba.
d) Comparación de los datos Obtenidos.
A través de la aplicación de la prueba de Goldfeld y Quandt se puede decir que existe Heterocedasticidad en
el modelo; bajo la prueba de Park no se pudo detectar la presencia de Heterocedasticidad, puesto que las
condiciones necesarias para la aplicación de esta prueba no se encontraban dadas.
Considerando la prueba de Spearman se puede afirmar que existen indicios de Heterocedasticidad por parte de
la variable Et.
e) Prueba de D − W para Autocorrelación Serial:
9
Del análisis de regresión lineal se desprenden los siguientes resultados bajo MCO
Ft = 2,353547 + 0,473013 Pt + 0,487835 Et + E
Parametro
Coeff
Error Stand
t − value
Sig Level
B0
B1
B2
2,353547
0,473013
0,487835
0,531831
0,023579
0,108628
4,4254
19,8336
4,4909
0,001
0,0000
0,0000
R2
SE
MAE
DW
0,8949
1,224324
0,951351
1,763
Un supuesto importante en el modelo de regresión lineal es que no hay correlación serial o autocorrelación
entre las perturbaciones ui consideradas dentro de la función de regresión poblacional.
Para detectar la no existencia de este supuesto se utilizara la prueba del estadístico d, de Durbin y Watson, el
cual define como la razón de la suma de las diferencias al cuadrado de residuales sucesivos sobre la suma
residuo cuadrado, considerando la siguiente formula.
D = Sumatoria ( ui − ui − 1) 2
Sumatoria ui2
1,763
0 dl dv 2 4−dv 4−dl 4
1.462 1.628 2.372 2.538
Como en la grafica se muestra, los valores dl y dv, son sacados de una tabla que esta expresada en un grado de
0.05 es decir 5% de significancia; considerando que nuestra muestra expuesta es de 49 observaciones, en la
tabla el valor que mas se asemeja a este valor (numero de observaciones) es 50 observaciones, la variables
utilizadas en el modelo son 2 Pt, Et . En vista de lo s análisis realizados se puede concluir la no existencia de
autocorrelación serial; es decir no hay correlación serial o autocorrelación entre las perturbaciones ui
consideradas dentro de la función de regresión poblacional.
10