Sistema numérico de Base 10 (decimal)

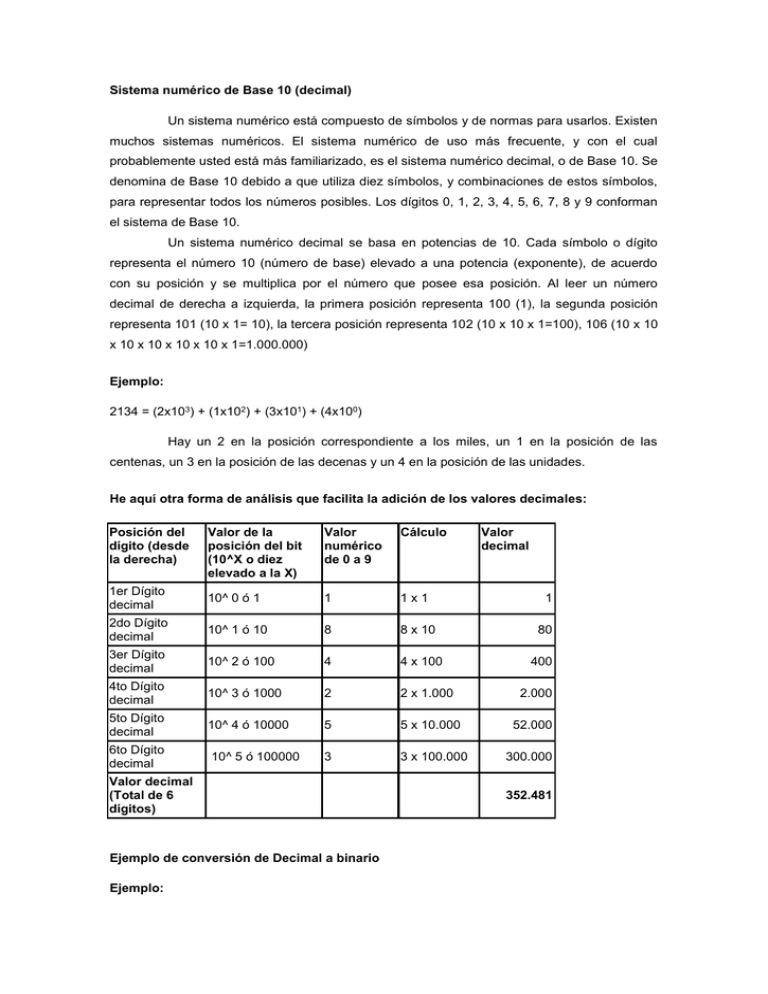
Sistema numérico de Base 10 (decimal)
Un sistema numérico está compuesto de símbolos y de normas para usarlos. Existen
muchos sistemas numéricos. El sistema numérico de uso más frecuente, y con el cual
probablemente usted está más familiarizado, es el sistema numérico decimal, o de Base 10. Se
denomina de Base 10 debido a que utiliza diez símbolos, y combinaciones de estos símbolos,
para representar todos los números posibles. Los dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 conforman
el sistema de Base 10.
Un sistema numérico decimal se basa en potencias de 10. Cada símbolo o dígito
representa el número 10 (número de base) elevado a una potencia (exponente), de acuerdo
con su posición y se multiplica por el número que posee esa posición. Al leer un número
decimal de derecha a izquierda, la primera posición representa 100 (1), la segunda posición
representa 101 (10 x 1= 10), la tercera posición representa 102 (10 x 10 x 1=100), 106 (10 x 10
x 10 x 10 x 10 x 10 x 1=1.000.000)
Ejemplo:
2134 = (2x103) + (1x102) + (3x101) + (4x100)
Hay un 2 en la posición correspondiente a los miles, un 1 en la posición de las
centenas, un 3 en la posición de las decenas y un 4 en la posición de las unidades.
He aquí otra forma de análisis que facilita la adición de los valores decimales:
Posición del
dígito (desde
la derecha)
Valor de la
posición del bit
(10^X o diez
elevado a la X)
Valor
numérico
de 0 a 9
Cálculo
1er Dígito
decimal
10^ 0 ó 1
1
1x1
1
2do Dígito
decimal
10^ 1 ó 10
8
8 x 10
80
3er Dígito
decimal
10^ 2 ó 100
4
4 x 100
400
4to Dígito
decimal
10^ 3 ó 1000
2
2 x 1.000
2.000
5to Dígito
decimal
10^ 4 ó 10000
5
5 x 10.000
52.000
6to Dígito
decimal
10^ 5 ó 100000
3
3 x 100.000
300.000
Valor decimal
(Total de 6
dígitos)
Ejemplo de conversión de Decimal a binario
Ejemplo:
Valor
decimal
352.481
Convertir el número decimal 192 en número binario.
192/2 = 96 con un residuo de 0
96/2
= 48 con un residuo de 0
48/2
= 24 con un residuo de 0
24/2
= 12 con un residuo de 0
12/2
= 6
con un residuo de 0
6/2
= 3
con un residuo de 0
3/2
= 1
con un residuo de 1
1/2
= 0
con un residuo de 1
Escriba todos los residuos, de atrás hacia adelante y obtendrá el número binario
11000000