Histograma

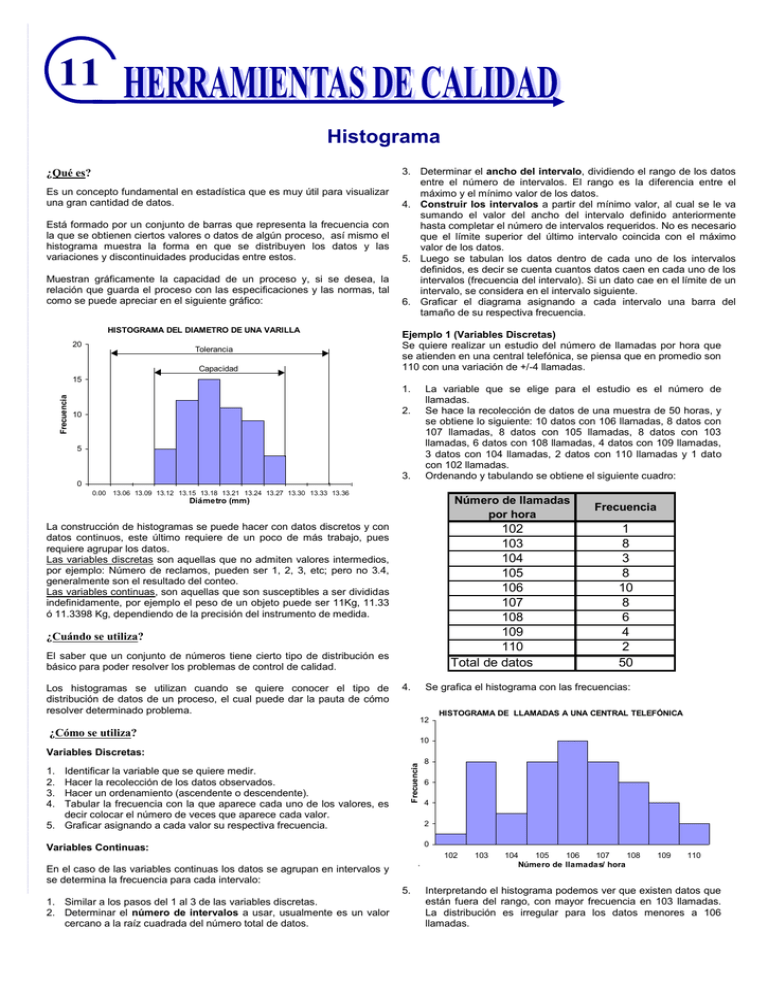
11
Histograma
¿Qué es?
Es un concepto fundamental en estadística que es muy útil para visualizar
una gran cantidad de datos.
Está formado por un conjunto de barras que representa la frecuencia con
la que se obtienen ciertos valores o datos de algún proceso, así mismo el
histograma muestra la forma en que se distribuyen los datos y las
variaciones y discontinuidades producidas entre estos.
Muestran gráficamente la capacidad de un proceso y, si se desea, la
relación que guarda el proceso con las especificaciones y las normas, tal
como se puede apreciar en el siguiente gráfico:
HISTOGRAMA DEL DIAMETRO DE UNA VARILLA
20
Tolerancia
Capacidad
3. Determinar el ancho del intervalo, dividiendo el rango de los datos
entre el número de intervalos. El rango es la diferencia entre el
máximo y el mínimo valor de los datos.
4. Construir los intervalos a partir del mínimo valor, al cual se le va
sumando el valor del ancho del intervalo definido anteriormente
hasta completar el número de intervalos requeridos. No es necesario
que el límite superior del último intervalo coincida con el máximo
valor de los datos.
5. Luego se tabulan los datos dentro de cada uno de los intervalos
definidos, es decir se cuenta cuantos datos caen en cada uno de los
intervalos (frecuencia del intervalo). Si un dato cae en el límite de un
intervalo, se considera en el intervalo siguiente.
6. Graficar el diagrama asignando a cada intervalo una barra del
tamaño de su respectiva frecuencia.
Ejemplo 1 (Variables Discretas)
Se quiere realizar un estudio del número de llamadas por hora que
se atienden en una central telefónica, se piensa que en promedio son
110 con una variación de +/-4 llamadas.
15
Frecuencia
1.
La variable que se elige para el estudio es el número de
llamadas.
Se hace la recolección de datos de una muestra de 50 horas, y
se obtiene lo siguiente: 10 datos con 106 llamadas, 8 datos con
107 llamadas, 8 datos con 105 llamadas, 8 datos con 103
llamadas, 6 datos con 108 llamadas, 4 datos con 109 llamadas,
3 datos con 104 llamadas, 2 datos con 110 llamadas y 1 dato
con 102 llamadas.
Ordenando y tabulando se obtiene el siguiente cuadro:
2.
10
5
3.
0
0.00 13.06 13.09 13.12 13.15 13.18 13.21 13.24 13.27 13.30 13.33 13.36
Número de llamadas
por hora
Diámetro (mm)
La construcción de histogramas se puede hacer con datos discretos y con
datos continuos, este último requiere de un poco de más trabajo, pues
requiere agrupar los datos.
Las variables discretas son aquellas que no admiten valores intermedios,
por ejemplo: Número de reclamos, pueden ser 1, 2, 3, etc; pero no 3.4,
generalmente son el resultado del conteo.
Las variables continuas, son aquellas que son susceptibles a ser divididas
indefinidamente, por ejemplo el peso de un objeto puede ser 11Kg, 11.33
ó 11.3398 Kg, dependiendo de la precisión del instrumento de medida.
102
103
104
105
106
107
108
109
110
Total de datos
¿Cuándo se utiliza?
El saber que un conjunto de números tiene cierto tipo de distribución es
básico para poder resolver los problemas de control de calidad.
Los histogramas se utilizan cuando se quiere conocer el tipo de
distribución de datos de un proceso, el cual puede dar la pauta de cómo
resolver determinado problema.
4.
Frecuencia
1
8
3
8
10
8
6
4
2
50
Se grafica el histograma con las frecuencias:
12
¿Cómo se utiliza?
HISTOGRAMA DE LLAMADAS A UNA CENTRAL TELEFÓNICA
10
Frecuencia
Variables Discretas:
1.
2.
3.
4.
Identificar la variable que se quiere medir.
Hacer la recolección de los datos observados.
Hacer un ordenamiento (ascendente o descendente).
Tabular la frecuencia con la que aparece cada uno de los valores, es
decir colocar el número de veces que aparece cada valor.
5. Graficar asignando a cada valor su respectiva frecuencia.
6
4
2
0
Variables Continuas:
102
En el caso de las variables continuas los datos se agrupan en intervalos y
se determina la frecuencia para cada intervalo:
5.
1. Similar a los pasos del 1 al 3 de las variables discretas.
2. Determinar el número de intervalos a usar, usualmente es un valor
cercano a la raíz cuadrada del número total de datos.
8
103
104
105
106
107
108
Número de llamadas/ hora
109
110
Interpretando el histograma podemos ver que existen datos que
están fuera del rango, con mayor frecuencia en 103 llamadas.
La distribución es irregular para los datos menores a 106
llamadas.
11
Intervalos
Ejemplo 2 (Variables Continuas)
58.5
62.8
67.1
71.4
75.7
80.0
84.3
88.6
92.9
97.2
101.5
Se quiere hacer un estudio del peso de los trabajadores de una
empresa:
1. La variable elegida para el estudio es el peso en kg de los
trabajadores. Se trata de una variable continua.
2. Se toma una muestra de 110 trabajadores y se mide el peso de
cada uno, tal como se presenta a continuación, previamente
ordenadas ascendentemente:
60.9
66.3
70.8
72.7
74.3
75.3
76.5
78.6
81.0
85.1
88.9
61.3
67.5
70.8
72.8
74.5
75.3
76.5
78.9
81.1
85.6
89.0
61.5
67.9
71.1
72.8
74.5
75.4
76.8
79.0
81.2
85.8
89.1
62.6
68.3
71.1
72.9
74.6
75.4
76.8
79.0
81.3
85.9
91.1
64.9
68.4
71.3
73.2
74.6
75.5
76.9
79.6
82.2
86.3
91.9
65.4
69.3
71.4
73.2
74.8
75.7
77.0
80.3
82.4
86.4
95.3
65.5
65.7
65.9
69.4
69.5
69.8
71.6
72.1
72.5
73.4
73.6
73.7
74.9
75.1
75.1
75.7
76.1
76.2
77.3
77.8
77.9
80.8
80.8
80.9
83.4
83.6
83.9
86.7
87.3
88.6
95.6 100.2 105.5
3. Una vez que se tienen los datos ordenados se determina el número
de intervalos:
N º int evalos  110 = 10.48  11
4. Determinando el ancho de intervalo:
Rango
# de int ervalos
=
105 .5  58.5
 4.27  4.3
11
5. Construyendo los intervalos y tabulando los datos se tiene:
5
7
15
30
19
14
10
6
2
1
1
HISTOGRAMA DE PESOS DE LOS TRABAJAODRES
35
_
x
30
25
20
15
10
5
0
58.5
Ancho 
62.8
67.1
71.4
75.7
80.0
84.3
88.6
92.9
97.2
101.5
105.8
6. A continuación se grafica el histograma:
Frecuencia
58.5
66.0
70.4
72.5
74.0
75.2
76.3
78.5
80.9
84.9
88.7
-
Frecuencia
62.8
67.1
71.4
75.7
80.0
84.3
88.6
92.9
97.2
101.5
Intervalos
7. Se puede observar que el peso promedio de los trabajadores se
encuentra entre 71.4 y 75.7 Kg.