PRACTICAS SALA INFORMÁTICA

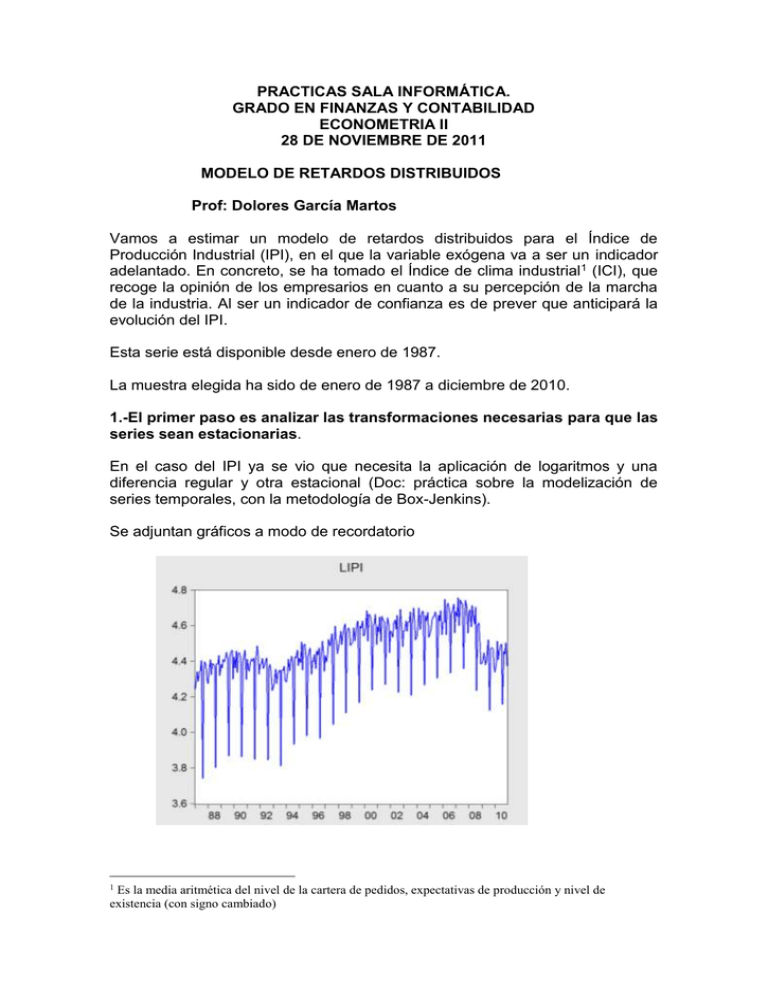
PRACTICAS SALA INFORMÁTICA.
GRADO EN FINANZAS Y CONTABILIDAD
ECONOMETRIA II
28 DE NOVIEMBRE DE 2011
MODELO DE RETARDOS DISTRIBUIDOS
Prof: Dolores García Martos
Vamos a estimar un modelo de retardos distribuidos para el Índice de
Producción Industrial (IPI), en el que la variable exógena va a ser un indicador
adelantado. En concreto, se ha tomado el Índice de clima industrial 1 (ICI), que
recoge la opinión de los empresarios en cuanto a su percepción de la marcha
de la industria. Al ser un indicador de confianza es de prever que anticipará la
evolución del IPI.
Esta serie está disponible desde enero de 1987.
La muestra elegida ha sido de enero de 1987 a diciembre de 2010.
1.-El primer paso es analizar las transformaciones necesarias para que las
series sean estacionarias.
En el caso del IPI ya se vio que necesita la aplicación de logaritmos y una
diferencia regular y otra estacional (Doc: práctica sobre la modelización de
series temporales, con la metodología de Box-Jenkins).
Se adjuntan gráficos a modo de recordatorio
1
Es la media aritmética del nivel de la cartera de pedidos, expectativas de producción y nivel de
existencia (con signo cambiado)
En relación con la serie ICI, hay que examinar si es una serie estacionaria o no.
El gráfico adjunto refleja la serie original. Al ser una serie de opiniones
empresariales no presentará un comportamiento tendencial. Igualmente, no
cabe esperar que presente estacionalidad.
Se comprueba que la serie no es estacionaria, al no presentar una media
constante, sino que exhibe oscilaciones de nivel. Por lo que pone de manifiesto
que será necesario tomar una primera diferencia regular. No obstante, habrá
que mirar el test de Dickey-Fuller para tomar la decisión.
El correlograma de la serie original no presenta punto de corte y decae muy
lentamente sin apenas anularse, señal de que podríamos estar ante una serie
no estacionaria.
Por su parte, el test de Dickey y Fuller presenta un valor de su test superior a
los valores críticos, por lo que se acepta la hipótesis nula de la existencia de
una raíz unitaria.
Por tanto, la transformación estacionaria de la serie ICI se consigue con la
primera diferencia regular. Tanto el gráfico de la serie transformada como su
correlograma avalan que se ha alcanzado la estacionariedad.
2.- Modelo de retardos distribuidos
En este caso, no hay una teoría económica que señale cual es el modelo que
explique el comportamiento dinámico del IPI en función del ICI. Se trata de un
indicador adelantado, por ello hay que analizar cuál es el modelo más
apropiado.
En la práctica de modelización de una serie temporal mensual, el modelo
estimado para el IPI era un
ARIMA (2,1,0) (2,1,1)12
Ahora bien, como se ha trabajado con una muestra más corta, conviene
analizar si para la muestra actual el modelo anterior sigue siendo válido.
Se observa que al modificar la muestra, el coeficiente del AR(24) no es
significativo. Así que lo eliminamos.
El modelo quedaría:
Teniendo en cuenta este modelo, estimemos un modelo aumentado en el que
se incluya el ICI como variable explicativa hasta un retardo p. Por ejemplo,
supongamos que la variable ICI entra en el modelo hasta el retardo 12.
En el modelo estimado se observa:
a) Hay una relación contemporánea entre el ICI y el IPI
b) Diversos retardos del ICI presentan parámetros significativos.
Teniendo en cuenta lo expuesto, procedemos a eliminar retardos no
significativos y en función del valor del criterio de Akaike aceptamos el modelo.
Modelo(retardos ICI)
0 a 12
Sin retardo 10
Sin retardo 8
Sin retardo 4
Sin retardo 3
AIC
-3.918
-3,925
-3,933
-3,94
-3,941
C Schwarz
-3,687
-3,708
-3,729
-3,75
-3,76
En concreto, el modelo con el menor AIC es el siguiente:
Log likelihood
532,19
532,16
532,15
523,09
531,25
El gráfico de los residuos presenta un comportamiento bastante aleatorio, sin
estructura. No obstante, será el correlograma el que nos permita concluir si es
compatible con un proceso ruido blanco.
El correlograma adjunto sugiere que habría que incluir una estructura de
retardos más compleja en el modelo en relación con el IPI. Aún cuando las
correlaciones de orden bajo (0,1,2) se encuentran en el borde de la
significatividad.
Se propone como modelo alternativo el siguiente. Como se puede comprobar el
criterio de AIC es ahora menor (-3,996). Incluso es menor que el valor que se
alcanzó con el modelo univariante (-3,70), lo que pone de manifiesto que el
modelo ADL es mejor.
Con fines predictivos, se pueden manejar ambos modelos; si bien, el modelo
ADL recogerá los movimientos que se produzcan en la economía
anticipadamente, al tratarse la variable explicativa de una variable de opiniones
de los empresarios que es más sensible que las variables que reflejan
producción, como el IPI.
El gráfico de los residuos muestra estructura de ruido blanco que corrobora el
correlograma.