EJERCICIOS DEL CURSO

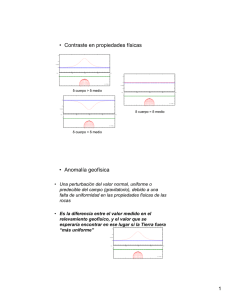
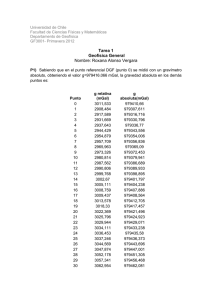
EJERCICIOS DEL CURSO
1. Determine la densidad del granito, sabiendo que sus componentes son:
35 % del volumen es cuarzo con una densidad de 2.65 gr/cm3
50 % del volumen es feldespato con una densidad de 2.55 gr/cm3
15 % del volumen es mica con una densidad de 3.15 gr/cm3
2. A partir de estudios sismológicos se sabe que la tierra está constituída por esferas
concéntricas:
Corteza:
espesor 35 km, densidad 2.80 gr/cm3
Manto:
espesor ?? km, densidad 4.60 gr/cm3
Núcleo:
espesor ?? km, densidad 10.85 gr/cm3
El radio medio de la tierra es 6370 km, la densidad promedio es 5.52 gr/cm3.
Calcule el radio del núcleo terrestre.
3. Cuales de las columnas A – F están en equilibrio con la columna X? Hacia donde se
moverían las demás? Densidades en gr/cm3.
4. Demuestre graficamente que la correción topográfica es normalmente siempre positiva.
E = Estación
Cerro:
E ____
Valle:
E_____
5. La tabla muestra las mediciones de la gravedad en una galería de una mina en
Rammelsberg/Harz, además la gravedad corregida por topografía, la gravedad
corregida por el efecto de las galerías, la altura sobre el nivel del mar y la descripción
geológica. Mediante la siguiente fórmula y conociendo el gradiente normal de
0.3086 mGal/m, calcule la densidad de cada intervalo de medición:
∆g = ∆h (∂γ/∂h - 4πfρ)
donde f = 6.67 x 10-8 cm3 gr-1 seg-2
6. Explique matematicamente porque la siguiente curva no podria ser el
resultado de una medición real:
7. Calcule la componente vertical de la gravedad gz en un punto P del eje central
de un cono cuya altura es z, radio r y densidad superficial u. Dé una solución
SIN integraciones.
Ayuda:
gz = f ∫ u dΩ
dΩ diferencial de ángulo sólido
f = 6.67 x 10-8 cm3 gr-1 seg-2
8. Sobre varias líneas de calibración de gravímetros, se sabe que las diferencias
de la gravedad son:
Harzburg – Torfhaus
München – Flensburg
Roma – Hammerfest
∆g = 85.15 mGal
∆g = 757.70 mGal
∆g = 2300.00 mGal
Con errores mp = 0.5 mGal. La relación
∆gp = (1 + ε) ∆gG
Con ∆gG las diferencias de gravedad medida con nuestro gravímetro, que
también tiene un error mG = 0.05 mGal, vincula ∆gP con ∆gG.
Determine mediante la ayuda da la función „Gauß´sches
Fehlerfortpflanzungsgesetz“ („Ley de propagación de errores de Gauß“) el
error en la determinación del factor de escala del gravímetro:
m
mc =

 ( x
i 1
i
f ( xi ) mi ) 2
9. Un hombre de 60 kg camina sobre el ecuador hacia el este, su velocidad es 1
m/seg. La gravedad está disminuída por el efecto de Eötvös, por lo tanto su
peso también. En cuántos gramos?
10. Calcule el valor de la ondulación del geoide N(x) para x = 0 que provoca una
masa puntual M ubicada a una profundidad d = 50 km. Su anomalía es en d =
0 km, ∆g = 300 mGal mientras que la gravedad normal es γ = 9.8 m/seg2.
Ayuda: Calcule primero las componentes horizontal y vertical de la gravedad
en x = 0. Calcule la desviación de la vertical como θ = gx/γ. La ondulación del
geoide está definida por:
N(x) = ∫ θ dx.
11. Qué magnitud tiene el ángulo de desviación de la vertical θ, sí la componente
horizontal gx es 10 mGal?
12. Pratt calculó para el meridiano λ = 77°.7 las siguientes desviaciones de la
vertical:
S1 (Φ = 39° 31`N) : 27.853``
S2 (Φ = 24° 07`N) : 11.968``
S3 (Φ = 18° 03`N) : 06.909``
Cuáles son los valores de la componente horizontal de la gravedad ?
γ = 9.79 m/seg2 y la dirección de x apunta al Norte.
13. Calcule la anomalía de Bouguer del cuerpo de la figura en las cuatro
estaciones, mediante el método de plantillas:
∆g = 2.328 x 10-4 N ∆  ∆Z ∆ρ
donde N el número de compartimentos determinados
∆  = 5°
∆ Z = 10 m
∆ρ
= -0.3 gr/cm3
Comentario: ∆g es dada en mGal si ∆  está en grados, ∆Z en metros y
∆ρ en gr/cm3.
14. En los modelos esquemáticos bidimensionales dados (horst, graben, fallas,
domo de sal, anticlinales, sinclinales, etc.) modefique parámetros relevantes
como: rechazo de la falla, ángulo de inclinación de la falla,
densidad/susceptibilidad, y en general su geometría y observe el efecto en la
anomalía que ello provoca.
15. Procese los datos de la „campaña de campo“ para obtener las anomalías de
Bouguer.
16. Modele las anomalías medidas en la „campaña de campo“.
17. Desarrolle un modelo tridimensional (en base a los modelos del ejercicio 14)
que justique la anomalía de Bouguer dada.