Formulario Geo 2D 030859 241209 5030

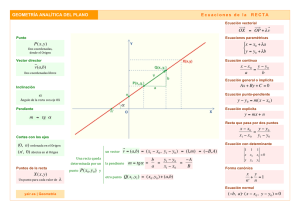
GEOMETRÍA ANALÍTICA DEL PLANO
Ecuación y Características de una RECTA
•
•
o
!
o
!
"
#
"
$
%
GEOMETRÍA ANALÍTICA DEL PLANO
DATOS
Ecuación y Características de una RECTA
I
Pasa por (x0, y0) y ...
Vector (a, b)
N
Vector
Otro punto
(a, b)
( x 1 , y1 ) =
( x 0 , y 0 ) + (a , b )
C
Ó
G
Pendiente Áng con OX
m=
b
a
α = arc tg m
N
I
T
A
S
Ec. general
Ec. implícita
x − x o y − y0
=
a
b
Despejar y
Gráfica
v(a, b)
P(x0, y0)
forma continua
(a , b ) =
Otro punto (x1, y1)
( x1 , y1 ) − ( x 0 , y 0 )
(a , b) = (1, m )
Pendiente m
Ángulo con OX
(x1, y1)
( x 1 , y1 ) =
( x 0 , y 0 ) + (1, m)
α
m=
(a , b) = ( − B, A )
Ax + By + C = 0
Ecuación implícita:
= ( B,− A )
(a , b) = (1, m )
y = mx + n
Gráfica:
x
*
*
y
*
*
m
x
0
*
y
n
*
(α, 0)
α
(0,β)
m=−
m
P(x0, y0)
α = arc tg m
m = tg α
Ecuación general:
Q(x1, y1)
y1 − y 0
x1 − x 0
A
B
Agrupar términos
P(x0,y0)
y − y 0 = m( x − x 0 )
α=arctg
m
α=
P(x0,y0)
α
α
α = arc tg m
Ax + By + C = 0
Despejar y
α = arc tg m
Agrupar términos
y = mx + n
x y
+ =1
α β
forma canónica
Q(*,*)
P(*,*)
n
Q(*,*)
GEOMETRÍA ANALÍTICA DEL PLANO
Vectores, distancias y ángulos
V E C T O R E S
Vector
módulo
dirección
sentido
v
u
Suma
Diferencia
u −v
Producto por
un número
Producto
escalar
r
α
a = r cos α
b = r sen α
u − v = ( a − a ' , b − b' )
v (a ' , b' )
coincidentes
u (a , b)
k ∈ℜ
u
α
u ⋅ v = u v cos α
u ( a , b)
v ( a ' , b' )
v ( a ' , b' )
A' x + B' y + C' = 0
v = k⋅u
( a ' , b' ) = k ( a , b )
A
B
=
A' B'
vectores proporcionales
coeficientes proporcionales
m = m'
( a ' , b' ) = k ( a , b )
pendientes iguales
y un punto común
vectores proporcionales
y un punto común
A
B C
= =
A' B' C'
pendientes iguales
m=−
ku = ( ka , kb)
perpendiculares
u ⋅ v = aa '+ bb'∈ ℜ
α
tg α =
ángulo α
1
m'
m − m'
1 + m ⋅ m'
m=0
D I S T AN C I A S
Q
d
punto–punto
recta horizontal
P ( x1 , y1 )
d ( P, Q) = PQ =
Q ( x2 , y 2 )
= ( x2 − x1 ) + ( y2 − y1 )
2
P
2
recta vertical
P ( x0 , y0 )
Punto–recta
P
d
r
d ( P, r ) =
Ax0 + By0 + C = 0
A2 + B 2
α = 0º
m=∞
α = 90º
m =1
r ≡ Ax + By + C = 0
diagonal
Ecuaciones:
Ax + B y+ C=0
m = m'
paralelas
Vectores:
u ( a , b)
m
m'
Rectas
a
se suma
el opuesto
ku
Pendientes:
u + v = ( a + a ' , b + b' )
u ( a , b)
v
u
r = a 2 + b2
b
b
tg α =
a
u ( a , b)
v ( a ' , b' )
u+v
−v
ÁN G U L O S
α = 45º
u⋅ v = 0
a ⋅ a ' + b ⋅ b' = 0
coeficientes proporcionales
A ⋅ A ' + B ⋅ B' = 0
vectores perpendiculares
cos α =
u⋅ v
u⋅v
cos α =
A ⋅ A' + B ⋅ B'
A 2 + B2 A' 2 + B' 2
(a ,0)
y=n
(0, b)
x =k
(1,1)
y =x+n
GEOMETRÍA ANALÍTICA DEL PLANO
DATOS
Pasa por ( ,
Vector (
,
Otro punto (
I
) y ...
)
,
)
Pendiente ______
Ángulo con OX _____
Ecuación general:
Ecuación implícita:
y=
Gráfica:
Hallar Ecuación y Características de una RECTA
Vector
Otro punto
N
C
Pendiente
Ó
Áng con OX
G
N
Ec. general
I
T
A
Ec. implícita
S
Gráfica
GEOMETRÍA ANALÍTICA DEL PLANO
DATOS
Pasa por ( ,
Vector (
,
Otro punto (
I
) y ...
)
,
)
Pendiente ______
Ángulo con OX _____
Ecuación general:
Ecuación implícita:
y=
Gráfica:
Hallar Ecuación y Características de una RECTA
Vector
Otro punto
N
C
Pendiente
Ó
Áng con OX
G
N
Ec. general
I
T
A
Ec. implícita
S
Gráfica