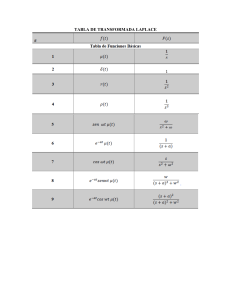
Transformada de Laplace.
La principal utilidad de la transformada de Laplace en Control de Procesos, es
que nos permite convertir una EDO en una EA, la cual es, usualmente, mas facil
de resolver.
La transformada de Laplace esta definida como la integral en el intervalo [0,∞],
para una funcion esta definida por
∞
F (s)=L { f (t)}=∫ f (t )e− st dt
0
Notas:
La funcion F(s) unicamente contiene informacion de f(t) para t>0.
Como la transformada de Laplace es una integral impropia no existe para todas
las funciones.
Algunas transformadas importantes.
Funcion escalon unitario.
La cual esta definida por u (t)= 0 t< 0
1 t≥0
Graficamente esta representada por:
{
}
Aplicando la transformada de Laplace, tenemos:
∞
∞
0
0
u ( s)=L {u (t)}=∫ u (t) e−st dt=∫ 1 e−st dt=¿ ?
Funcion impulso unitario.
Tambien es conocida como la funcion delta de Dirac, δ(t). Es una funcion
idealizada que tiene un area unitaria, formada por un rectangulo de base 0 y
altura infinita, la cual sucede a tiempo 0.
0 t <0
δ(t )= 1 t=0
0 t >0
Graficamente se representa como:
{
}
La transformada de Laplace esta dada por:
∞
δ( s)=L {δ(t)}=∫ δ (t) e−st dt=¿ ?
0
Funcion exponencial.
Para la funcion f (t)=e−at para
transformada esta dada por
t≥0 donde a es una constante positiva, la
Funcion rampa.
La funcion rampa esta definida por f (t)=α t donde α≠0 .
En el caso donde la pendiente es 1, la grafica esta dada por:
La transformada de la funcion rampa se expresa como:
(Autoestudio) Transformada de Laplace de las funciones trigonometricas.
Algunas propiedades de las trasformadas de Laplace.
Linealidad.
Traslacion compleja
Traslacion en el tiempo
Derivada.
1er orden
nth orden
Convolucion.
Si F (s)=L { f (t )} y
esta definida por
G(s )=L {g (t)}
existen, entonces la convolucion de f(t)*g(t)
t
t
f (t)∗g (t )=∫ f (t−τ) g (τ ) d τ=∫ f ( τ) g (t−τ ) d τ
0
y la transformada de Laplace esta dada por
Ejemplos de transformadas de Laplace.
o
L { f (t)∗g (t)}=F (s)G(s)
.
Transformada inversa de Laplace.
Una vez que hemos obtenido una expresion algebraica en el plano s para una
ecn. Diferencial, queremos obtener la solucion en el tiempo.
⃗
Y (s)
L−1
y (t)
Para esto, podemos expresar la funcion Y(s) en fracciones parciales, i.e.
Y ( s )=
G N (s ) N 1 ( s ) N 2 ( s) N 3 (s)
=
+
+
+...
G D (s) D 1 ( s) D 2 ( s) D 3 (s)
Para expandir una funcion en fracciones parciales, hay que encontrar las raices
del polinomio GD(s). Dependiendo de la forma de las raices tenemos 3 casos.
Caso 1. Raices reales diferentes.
Y ( s )=
G N (s )
G N (s)
=
G D (s) (s−s1 )( s−s 2) ...( s−sn )
en fracciones parciales se expresa como:
A1
A2
An
Y ( s )=
+
+...+
s−s 1 s−s 2
s−sn
donde las Ai's son constantes por determinar, las cuales se obtienen mediante
Caso 2. Raices reales repetidas.
G ( s)
G N(s)
Y ( s )= N =
G D ( s ) ( s−s1 )( s−s 2) ...( s−s j )r ... (s−s n )
en fracciones parciales se expresa como:
A j (r −1 )
A j (1)
A
A
A jr
A
Y ( s )= 1 + 2 +...+
+
+..+
+...+ n
r
r−1
s−s 1 s−s 2
( s−s j )
s−s n
(s−s j ) ( s−s j )
donde las Aj's se calculan mediante:
Caso 3. Factores de 2do orden.
Se pueden trabajar de 2 formas.
a) usando raices complejas se convierte en el caso 1 o 2.
b) usando una ecn. Cuadratica y expresando la fraccion parcial como
A
A
A
Bs+C
Y ( s )= 1 + 2 +...+ 2
+...+ n
s−s 1 s−s 2
s−s n
as +bs +c
donde las constantes B, C , a, b y c se obtienen mediante un sistema de
ecuaciones lineales.