1.1.
MARCO TEÓRICO
1.1.1. CONCEPTOS Y DEFINICIONES BASICAS
• Viga
Se denomina viga a un elemento estructural lineal que trabaja principalmente a flexión, en
ellas la longitud predomina sobra las otras dos dimensiones y suele ser horizontal.
• Módulo de Elasticidad o módulo de Young
Es un parámetro que caracteriza el comportamiento de un material elástico, según la dirección
en la que se aplica una fuerza.
Para un material elástico e isótropo, el módulo de Young tiene el mismo valor para una
tracción que para una compresión, siendo una constante independiente del esfuerzo siempre
que no exceda del valor máximo denominado limite elástico, y es siempre mayor que cero.
El módulo de elasticidad es una constante elástica, que al igual que el límite elástico puede
encontrarse empíricamente mediante un ensayo de tracción del material.
• Momento de inercia
El momento de inercia es una medida de la inercia rotacional del cuerpo, cuando un cuerpo
gira en torno a los ejes principales de inercia, la inercia rotacional puede ser representada
como magnitud escalar llamada momento de inercia.
El momento de inercia refleja la distribución de masa de un cuerpo o de un sistema de
partículas en rotación, respecto a un eje de giro. El momento de inercia solo depende de la
geometría del cuerpo y de la posición del eje de giro; pero no dependen de las fuerzas que
intervienen en el movimiento
• Flexión
Se denomina flexión al tipo de deformación que representa un elemento estructural alargado
en una dirección perpendicular a su eje longitudinal.
Las vigas o arcos son elementos estructurales pensados para trabajar predominantemente en
flexión, geométricamente son prismas mecánicos cuya rigidez depende, entre otras cosas, del
momento de inercia de la sección transversal de la viga
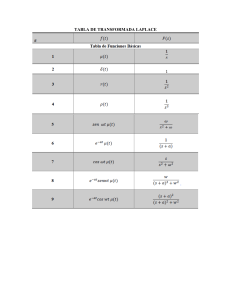
1.1.2. Transformada de Laplace
Sea la función 𝑓(𝑡) una función continua por tramos o en todo su dominio. La
Transformada de Laplace de 𝑓(𝑡) es denotada como ℒ{𝑓(𝑡)} y se define como la
integral impropia. (DiPrima, 2010).
De la definición anterior, se tiene una notación alternativa para las transformaciones de
Laplace. Por conveniencia, a menudo se denotará la transformada de Laplace como:
ℒ{𝑓(𝑡)} = 𝐹(𝑠)
Con esta notación alternativa, tenga en cuenta que la transformada de Laplace es realmente
una función de una nueva variable, esta variable es “𝑠” y toda la expresión que depende de 𝑡
en la función se abandonará en el proceso de integración. Ahora, la integral en la definición
de la transformación es una integral impropia y probablemente sería mejor recordar cómo
funcionan este tipo de integrales antes de poder calcular algunas transformaciones (Lang,
1980).
Adicionalmente, una función continua por tramos o también llamada seccionalmente
continua, es aquella que es continua en todo su dominio excepto en una cantidad finita de
puntos, un ejemplo se muestra en la siguiente figura (William Boyce, 2010).
Propiedades de la Transformada de Laplace
La transformada de Laplace posee muchas propiedades que se aplican tanto en su definición
como en su aplicación a los problemas de valor inicial (PVI) de las ecuaciones diferenciales,
entre estas se tiene:
Propiedad de Linealidad
Sean 𝑓(𝑡) y 𝑔(𝑡) dos funciones, entonces:
ℒ{𝛼𝑓(𝑡) + 𝛽𝑔(𝑡)} = 𝛼ℒ{𝑓(𝑡) } + 𝛽ℒ{𝑔(𝑡) }
Para cualquier constante 𝛼, 𝛽 ∈ 𝑅.
Propiedad de cambio de escala
Sea 𝑓(𝑡) una función con transformada de Laplace 𝐹(𝑠) y sea 𝛼 ∈ 𝑅 − {0}, entonces:
Propiedad de desplazamiento
Sea 𝑓(𝑡) una función con transformada de Laplace 𝐹(𝑠), entonces:
Para cualquier constante 𝑎 ∈ 𝑅.
Propiedad de la derivada
Sea 𝑓(𝑡) una función derivable con transformada de Laplace 𝐹(𝑠) y cuyo valor inicial 𝑓(0)
está definido, entonces:
Propiedad de la segunda derivada
Sea 𝑓(𝑡) una función dos veces derivable con transformada de Laplace 𝐹(𝑠) y cuyos valores
iniciales 𝑓(0), 𝑓′ (0) están definidos, entonces:
Propiedad de la n-ésima derivada
Sea 𝑓(𝑡) una función n veces derivable con transformada de Laplace 𝐹(𝑠) y cuyos
valores iniciales 𝑓(0), 𝑓′ (0), …, 𝑓(𝑛−1) (0) están definidos, entonces:
Propiedad de la integral
Sea 𝑓(𝑡) una función integrable con transformada de Laplace 𝐹(𝑠), entonces:
TRASFORMADA DE LAPLACE EN DEFORMACIONES DE VIGA
Consideremos una viga delgada de longitud L y sea y(x) su desplazamiento transversal, a una
distancia x medida desde uno de los extremos, de la posición original debido a la carga.
Entonces, de la teoría elemental de las vigas, tenemos: EI (d^4 y)/(dx^4 )=-W(x) Donde:
W(x) es la fuerza transversal por unidad de longitud, considerando la dirección positiva hacia
abajo y EI es la rigidez de flexión de la viga (E es el módulo de elasticidad de Young e I es el
momento de inercia de a viga alrededor de su eje central). Se supone que la viga tiene
propiedades uniformes de elasticidad y una sección transversal uniforme en toda su longitud,
así que tanto E como I se toman como constantes.
La ecuación se escribe algunas veces como:
Donde: y(x) es su desplazamiento transversal medido hacia abajo y no hacia arriba.
Deflexión transversal de una viga: (a) posición inicial. (b) posición desplazada.
VIGA VOLADIZA
Las vigas voladizas se encuentran frecuentemente en la construcción, especialmente en
puentes en voladizo y balcones. En los puentes, los voladizos se construyen habitualmente en
parejas, de manera que cada uno sostiene una parte de voladizo. Una sección central. El Forth
Bridge de Escocia es un ejemplo de puente de celosía en En la construcción también se usan a
menudo voladizos temporales, es decir, cuando la estructura está en obras hay un voladizo,
que sin embargo cuando la estructura se completa no actúa como voladizo. Esto es muy útil
cuando no se pueden usar apoyos temporales, como cimbras o puntales, para sostener la
estructura mientras se está construyendo.
METODO DE DOBLE INTEGRACIÓN:
Es el más general para determinar deflexiones. Se puede usar para resolver casi cualquier
combinación de cargas y condiciones de apoyo en vigas estáticamente determinadas e
indeterminadas. Su uso requiere la capacidad de escribir las ecuaciones de los diagramas de
fuerza cortante y momento flector y obtener posteriormente las ecuaciones de la pendiente y
deflexión de una viga por medio del cálculo integral. El método de doble integración produce
ecuaciones para la pendiente la flexión en toda la viga y permite la determinación directa del
punto de máxima deflexión. Ecuación diferencial de la elástica:
𝑑2𝑦
𝑀
=
𝑑𝑥 2
𝐸𝐼
El producto de “E.I” se conoce como la rigidez a flexión y en caso de que varié a lo largo de
la vida, como es el caso de una viga de sección transversal variable. Debe expresarse en una
función de “x” antes de integrar la ecuación diferencial.