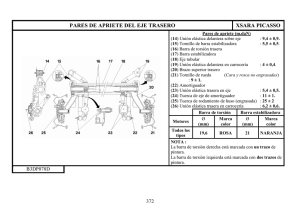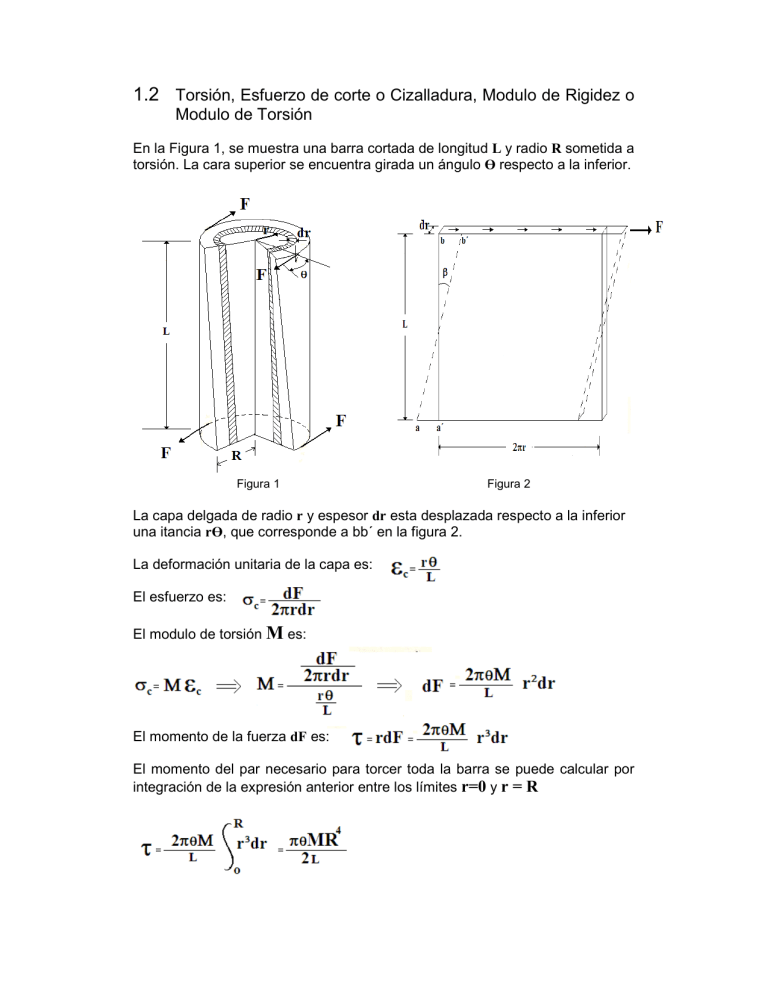
1.2 Torsión, Esfuerzo de corte o Cizalladura, Modulo de Rigidez o Modulo de Torsión En la Figura 1, se muestra una barra cortada de longitud L y radio R sometida a torsión. La cara superior se encuentra girada un ángulo Ө respecto a la inferior. Figura 1 Figura 2 La capa delgada de radio r y espesor dr esta desplazada respecto a la inferior una itancia rӨ, que corresponde a bb´ en la figura 2. La deformación unitaria de la capa es: El esfuerzo es: El modulo de torsión M es: El momento de la fuerza dF es: El momento del par necesario para torcer toda la barra se puede calcular por integración de la expresión anterior entre los límites r=0 y r = R Análogamente a la Ley de Hooke: F = Kx tenemos De la teoría del pendulo de torsión para Ө pequeño, donde I es el momento de inercia para el cuerpo suspendido. PROCEDIMIENTO 1. Medir las constantes L, R de la barra. 2. Medir m, R´ del disco y calcular su momento de inercia I. 3. Girar el disco un ángulo pequeño y soltar dejando que se estabilice la oscilación. 4. Medir el tiempo t para 10 oscilaciones 5. Obtener T= t/10 6. Calcular k y M correspondientes 7. Llenar la tabla siguiente: Ө t T k M 8. Graficar k vs Ө y M vs Ө y ajustar para obtener los valores óptimos de k y M de la muestra