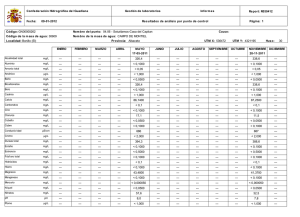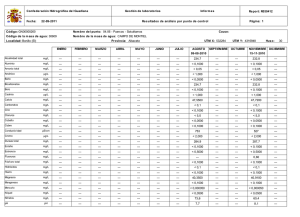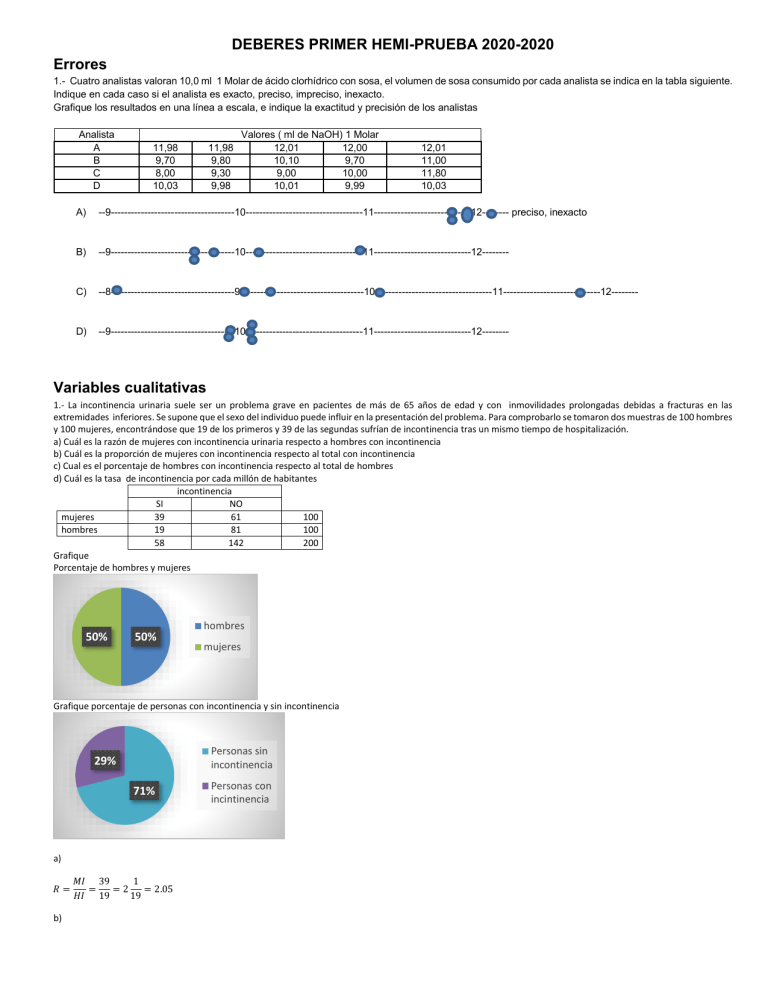
DEBERES PRIMER HEMI-PRUEBA 2020-2020 Errores 1.- Cuatro analistas valoran 10,0 ml 1 Molar de ácido clorhídrico con sosa, el volumen de sosa consumido por cada analista se indica en la tabla siguiente. Indique en cada caso si el analista es exacto, preciso, impreciso, inexacto. Grafique los resultados en una línea a escala, e indique la exactitud y precisión de los analistas Analista A B C D 11,98 9,70 8,00 10,03 11,98 9,80 9,30 9,98 Valores ( ml de NaOH) 1 Molar 12,01 12,00 10,10 9,70 9,00 10,00 10,01 9,99 12,01 11,00 11,80 10,03 A) --9-------------------------------------10-----------------------------------11-----------------------------12-------- preciso, inexacto B) --9-------------------------------------10-----------------------------------11-----------------------------12-------- C) --8-------------------------------------9-------------------------------------10-----------------------------------11-----------------------------12-------- D) --9-------------------------------------10-----------------------------------11-----------------------------12-------- Variables cualitativas 1.- La incontinencia urinaria suele ser un problema grave en pacientes de más de 65 años de edad y con inmovilidades prolongadas debidas a fracturas en las extremidades inferiores. Se supone que el sexo del individuo puede influir en la presentación del problema. Para comprobarlo se tomaron dos muestras de 100 hombres y 100 mujeres, encontrándose que 19 de los primeros y 39 de las segundas sufrían de incontinencia tras un mismo tiempo de hospitalización. a) Cuál es la razón de mujeres con incontinencia urinaria respecto a hombres con incontinencia b) Cuál es la proporción de mujeres con incontinencia respecto al total con incontinencia c) Cual es el porcentaje de hombres con incontinencia respecto al total de hombres d) Cuál es la tasa de incontinencia por cada millón de habitantes incontinencia SI NO mujeres 39 61 100 hombres 19 81 100 58 142 200 Grafique Porcentaje de hombres y mujeres 50% 50% hombres mujeres Grafique porcentaje de personas con incontinencia y sin incontinencia Personas sin incontinencia 29% 71% a) 𝑅= b) 𝑀𝐼 39 1 = =2 = 2.05 𝐻𝐼 19 19 Personas con incintinencia 𝑅= 𝑀𝐼 39 = = 0,67 𝑇𝐼 58 c) 𝑅= 𝐻𝐼 19 = = 0,19 → 19% 𝑇𝐻 100 d) 𝑇= 𝑇𝐼 58 29 = × 1000000 = × 1000000 = 290000 𝑇𝑇 200 100 La tasa de personas con incontinencia es de 290000 por cada millón de habitantes 2.- Dado las frecuencias por zona y sector en la tabla siguiente Calcule las frecuencias relativas y grafique el porcentaje de frecuencias relativas por Zona Sector Zona Rural Urbano Zona Rural Urbano Sector Frecuencia Cayambe Santo Domingo I Santo Domingo II Cayambe-Paquistancia Cariacu San Pablo Urco Mercado diario Mercado central Mercado mayor Sector Cayambe Santo Domingo I Santo Domingo II Cayambe-Paquistancia Cariacu San Pablo Urco Total rural Mercado diario Mercado central Mercado mayor Total urbano 41 25 56 52 13 21 16 29 19 Frecuencia fr 41 25 56 52 13 21 208 16 29 19 64 0,1971 0,1202 0,2692 0,2500 0,0625 0,1010 0,5517 1,0000 0,6552 - Rural 6% 10% 20% 12% 25% 27% Cayambe Santo Domingo I Santo Domingo II Cayambe-Paquistancia Cariacu San Pablo Urco Urbano 25% 30% 45% Mercado diario Mercado central Mercado mayor 3.- En los resultados de un análisis de los productos devueltos por el clientes se detectó los siguientes problemas (ver tabla). a) Realice un diagrama de barras Quejas de clientes Frecuencia de errores Entrega tarde Entrega equivocada Mal facturado Mala calidad del producto Producto no solicitado Mal etiquetado Cartón aplastado Descongelado otros 3 39 39 8 44 12 1 3 2 Frecuencia de errores otros 2 Descongelado 3 Cartón aplastado 1 Mal etiquetado 12 Producto no solicitado 44 Mala calidad del producto 8 Mal facturado 39 Entrega equivocada 39 Entrega tarde 3 0 10 20 30 40 50 Variables cuantitativas Medidas de tendencia central, medidas de tendencia no central y medidas de dispersión y gráficos 1.- Dados los datos (sin agrupar) 23 25 26 23 21 24 Calcule a.- Media, mediana, moda, media mediana moda 24,05 24 23 22 23 24 26 24 23 25 26 27 21 23 25 22 28 b.- Desviación estándar, varianza, CV, N Datos ordenados (xi) 21 21 22 22 23 23 23 23 23 24 24 24 25 25 25 26 26 26 27 28 481 Datos 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 23 25 26 23 21 24 22 23 24 26 24 23 25 26 27 21 23 25 22 28 Total |xi-media| 3,0500 3,0500 2,0500 2,0500 1,0500 1,0500 1,0500 1,0500 1,0500 0,0500 0,0500 0,0500 0,9500 0,9500 0,9500 1,9500 1,9500 1,9500 2,9500 3,9500 31,2000 (xi-media)^2 9,3025 9,3025 4,2025 4,2025 1,1025 1,1025 1,1025 1,1025 1,1025 0,0025 0,0025 0,0025 0,9025 0,9025 0,9025 3,8025 3,8025 3,8025 8,7025 15,6025 70,9500 Desviación estándar ∑(𝑥𝑖 − 𝑥̅𝑖 )2 ∑(𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)2 70,95 𝑆=√ =√ =√ = 1,9324 𝑛−1 𝑛−1 20 − 1 Varianza 𝑆2 = ∑(𝑥𝑖 − 𝑥̅𝑖 )2 ∑(𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)2 70,95 = = = 3,7342 𝑛−1 𝑛−1 20 − 1 CV 𝐶𝑉 = 𝑆 × 100 𝑆 × 100 1,9324 × 100 = = = 8,0349 % 𝑥̅𝑖 𝑚𝑒𝑑𝑖𝑎 24,05 c.- Cuartil 2, quintil 2, decil 4, percentil 67 posición Cuartil 2 (Q) Quintil 2 (q) Decil 4 (d) Percentil 67 (p) 10 8 8 13,4 posición decimal 25+(25-25)*0,4 Valor 2.- Con los datos siguientes calcule a.- La media, la mediana, la moda b.- La desviación estándar, la varianza, el coeficiente de variación c.- Cuartil 2, decil 4, quintil 2, percentil 45 a) Total media mediana moda xi (ordenado) 6 10 9 7 8 40 7,86 8 5 fi (ordenado) 5 5 8 15 17 50 24 23 23 25 xi fi 6 7 8 9 10 fA 5 15 17 8 5 5 20 37 45 50 b) xi 6 7 8 9 10 40 Total fi 5 15 17 8 5 50 fA 5 20 37 45 50 xi*fi 30 105 136 72 50 393 xi-media -1,86 -0,86 0,14 1,14 2,14 ((xi-media)^2)*fi 17,30 11,09 0,33 10,40 22,90 62,02 ∑(𝑥𝑖 − 𝑥̅𝑖 )2 × 𝑓𝑖 ∑(𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)2 × 𝑓𝑖 62,02 𝑆=√ =√ =√ = 1,1137 𝑓𝑖 𝑓𝑖 40 Varianza 𝑆2 = ∑(𝑥𝑖 − 𝑥̅𝑖 )2 × 𝑓𝑖 ∑(𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)2 × 𝑓𝑖 62,02 = = = 1,2404 𝑓𝑖 𝑓𝑖 40 CV 𝐶𝑉 = 𝑆 × 100 𝑆 × 100 1,1137 × 100 = = = 14,1696 % 𝑥̅𝑖 𝑚𝑒𝑑𝑖𝑎 7,86 3.- Con los siguientes datos, calcule el coeficiente de simetría y curtosis clases 90 98 106 114 122 130 138 97 105 113 121 129 137 145 fi fA 7 9 13 3 4 3 1 40 7 16 29 32 36 39 40 media desviación estándar clases 90-97 98-105 106-113 114-121 122-129 130-137 138-145 Marca de clase (xi) 93,5 101,5 109,5 117,5 125,5 133,5 141,5 fi 7 9 13 3 4 3 1 fA 7 16 29 32 36 39 40 xi*fi xi-media ((xi-media)^2)*fi fi*((xi-media)^3) fi*((xi-media)^4) 654,5 913,5 1423,5 352,5 502 400,5 141,5 4388 -16,2 -8,2 -0,2 7,8 15,8 23,8 31,8 1837,08 605,16 0,52 182,52 998,56 1699,32 1011,24 6334,4 -29760,70 -4962,31 -0,10 1423,66 15777,25 40443,82 32157,43 55079,04 482123,28 40690,96 0,02 11104,52 249280,52 962562,82 1022606,34 2768368,45 109,7 12,58 Coeficiente de simetría ∑ 𝑓𝑖 × (𝑥𝑖 − 𝑥̅𝑖 )3 ∑ 𝑓𝑖 × (𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)3 55079,04 = = = 0,69 𝑁 × 𝑆3 𝑁 × 𝑆3 40 × 12,583 As > 0 por lo tanto tiene asimetría positiva 𝐴𝑠 = Curtosis 𝑔= ∑ 𝑓𝑖 × (𝑥𝑖 − 𝑥̅𝑖 )4 ∑ 𝑓𝑖 × (𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎)4 2768368,45 −3= = − 3 = −0,24 𝑁 × 𝑆4 𝑁 × 𝑆4 40 × 12,584 g < 0 por lo tanto distribución platicúrtica 4- Se sabe que el porcentaje de alcohol en vino debe ser de 11°, se toma del mercado muestras de tres marcas de vino para comprobar el contenido alcohólico, se analizan por tres laboratorios diferentes obteniéndose los siguientes resultados: Calcule Medias, desviaciones estándares, CV Calcule el error absoluto y relativo de cada laboratorio Analice los datos anteriores y elija conque laboratorio trabajaría valores X1 X2 X3 X4 X5 Laboratorio 1 12,5 12,8 12,4 13,5 13,2 Laboratorio 2 10,8 10,4 11,0 12,8 13,5 Laboratorio 3 11,3 10,8 11,0 11,4 10,8 valores X1 X2 X3 X4 X5 Total Laboratorio Laboratorio Laboratorio 1 2 3 12,5 10,8 11,3 12,8 10,4 10,8 12,4 11 11 13,5 12,8 11,4 13,2 13,5 10,8 64,4 58,5 55,3 media Desviación estándar CV Laboratorio 1 12,88 0,4167 3,2349 xi-media laboratorio1 -0,38 -0,08 -0,48 0,62 0,32 Laboratorio 2 11,70 1,2198 10,4259 xi-media laboratorio2 -0,9 -1,3 -0,7 1,1 1,8 xi-media laboratorio3 0,24 -0,26 -0,06 0,34 -0,26 (xi-media)^2 laboratorio1 0,1444 0,0064 0,2304 0,3844 0,1024 0,868 (xi-media)^2 laboratorio2 0,81 1,69 0,49 1,21 3,24 7,44 (xi-media)^2 laboratorio3 0,0576 0,0676 0,0036 0,1156 0,0676 0,312 Laboratorio 3 11,06 0,2498 2,2586 Error absoluto 𝐸𝐴 = 𝑥𝑖 − 𝜇 𝐸𝐴1 = 12,88 − 11 = 1,88 𝐸𝐴2 = 11,7 − 11 = 0,7 𝐸𝐴3 = 11,06 − 11 = 0,06 Error relativo 𝐸𝑅 = 𝑥𝑖 − 𝜇 ∗ 100 𝜇 𝐸𝑅1 = 12,88 − 11 ∗ 100 = 0,1709 11 𝐸𝑅2 = 11,7 − 11 ∗ 100 = 0,0636 11 𝐸𝑅3 = 11,06 − 11 ∗ 100 = 0,0054 11 Se elije el laboratorio 3 debido a su baja desviación estándar y poco error tanto relativo como absoluto 5.- Calcule el resultado con su desviación estándar [ (14,3 ± 0,2) – (11,6 ± 0,2)] x (0,050 ± 0,001) [ (820 ± 10) + (1030 ± 5)] x (42,23 ± 0,4) = [ (2,7 ± 𝑆𝑌1 )] x (0,050 ± 0,001) [ (1850 ± 𝑆𝑌2 )] x (42,23 ± 0,4) 𝑆𝑌1 = √0,22 + 0,22 = 0,2828 𝑆𝑌2 = √102 + 52 = 11,1803 = [ (2,7 ± 0,2828)] x (0,050 ± 0,001) [ (1850 ± 11,1803)] x (42,23 ± 0,4) = 1,728 × 10−6 ± 𝑆𝑌3 0,2828 2 0,001 2 11,1803 2 0,4 2 𝑆𝑌3 = 1,728 × 10−6 × √( ) +( ) +( ) +( ) 2,7 0,050 1850 42,23 𝑆𝑌3 = 1,8528 × 10−7 𝑅 = 1,728 × 10−6 ± 1,8528 × 10−7 6.- Se hace un estudio de la precisión interdía de un método para determinar glucosa en sangre, para ello se mide la concentración de los reactivo de control durante 30 días consecutivos, se considera que la precisión del método es aceptable si el coeficiente de variación (CV) del método es menor o igual a 1/3 del error total dado por el CLIA, el cual para la glucosa está especificado en el 10%. La desviación estándar interdía y el CV del método se calculan con las siguientes fórmulas, en donde D = Número de días D = 30 días Sb = desviación estándar inerdía CVb = Coeficiente de variación interdía Xd = valor determinado en el día Xt = media Diga si la precisión del método es aceptable o no Días día 1 día 2 día 3 día 4 día 5 día 6 día 7 día 8 día 9 día 10 día 11 día 12 día 13 día 14 día 15 Días día 1 día 2 día 3 día 4 día 5 día 6 día 7 día 8 día 9 día 10 día 11 día 12 día 13 día 14 día 15 día 16 día 17 día 18 día 19 día 20 día 21 día 22 día 23 día 24 día 25 día 26 día 27 día 28 día 29 día 30 Total media Sb CV Xd (valores) Glucosa mg/dl 13,4 13,7 13,5 13,7 13,6 13,8 13,7 13,4 13,3 13,5 13,7 13,6 13,4 13,2 13,2 Xd (valores) Glucosa mg/dl 13,4 13,7 13,5 13,7 13,6 13,8 13,7 13,4 13,3 13,5 13,7 13,6 13,4 13,2 13,2 13,7 13,6 13,8 13,5 13,7 13,6 13,4 13,2 13,2 13,7 13,4 13,3 13,5 13,7 13,6 405,6 Días día 16 día 17 día 18 día 19 día 20 día 21 día 22 día 23 día 24 día 25 día 26 día 27 día 28 día 29 día 30 Xd-Xt (Xd-Xt)^2 -0,12 0,18 -0,02 0,18 0,08 0,28 0,18 -0,12 -0,22 -0,02 0,18 0,08 -0,12 -0,32 -0,32 0,18 0,08 0,28 -0,02 0,18 0,08 -0,12 -0,32 -0,32 0,18 -0,12 -0,22 -0,02 0,18 0,08 0,0144 0,0324 0,0004 0,0324 0,0064 0,0784 0,0324 0,0144 0,0484 0,0004 0,0324 0,0064 0,0144 0,1024 0,1024 0,0324 0,0064 0,0784 0,0004 0,0324 0,0064 0,0144 0,1024 0,1024 0,0324 0,0144 0,0484 0,0004 0,0324 0,0064 1,028 13,52 0,1883 1,3926% La precisión es aceptable ya que tiene un CV (1,3926%) menor al 10% 7.- Con los datos de la siguiente tabla a) Realice un histograma b) Realice un gráfico de bigotes c) Trasforme la variable cuantitativa a cualitativa use las categorías Bajo peso (≤ 60 Kg) Normal (> 60 ≤ 80 Kg) Xd (valores) Glucosa mg/dl 13,7 13,6 13,8 13,5 13,7 13,6 13,4 13,2 13,2 13,7 13,4 13,3 13,5 13,7 13,6 Alto (> 80kg) 66,7 75,6 57,0 60,2 65,0 53,6 62,2 68,4 71,4 71,4 64,5 55,7 82,2 77,5 70,5 89,8 60,1 66,9 58,9 32,0 51,5 64,4 52,0 61,6 59,5 a) b) 94,4 77,4 71,7 53,1 40,9 72,4 53,8 29,6 82,4 83,2 74,1 22,5 63,4 58,0 62,0 53,0 59,2 29,4 72,9 88,7 70,9 89,9 60,4 75,7 64,2 Peso en kg 78,5 50,5 35,6 67,4 34,5 46,8 40,0 48,2 28,1 65,9 65,8 87,4 95,9 74,0 29,0 23,4 24,5 68,1 17,8 74,0 34,5 68,9 96,0 77,9 29,0 71,8 74,5 70,0 81,5 55,3 56,3 62,8 25,0 71,4 76,5 23,3 67,0 32,9 17,8 70,6 61,0 89,8 25,0 25,8 66,5 72,5 50,0 64,8 74,6 64,6 60,7 60,5 32,6 66,1 65,0 46,5 77,3 74,5 84,5 40,0 89,0 54,3 55,0 64,6 61,0 59,0 84,5 20,0 28,2 63,8 75,0 78,0 76,1 69,9 65,2 73,2 50,4 75,8 72,6 62,0 92,4 58,0 19,5 53,2 56,7 54,7 68,0 74,6 74,3 92,1 73,3 22,1 29,1 43,4 67,9 71,8 47,6 69,6 77,3 56,1 c) 17,8 17,8 19,5 20 22,1 22,5 23,3 23,4 24,5 25 25 25,8 28,1 28,2 29 29 29,1 29,4 29,6 32 32,6 32,9 34,5 34,5 35,6 IMC (Kg) ≤ 60 Kg > 60 ≤ 80 Kg > 80kg Peso en kg (Datos ordenados) 40 56,7 64,6 71,4 40 57 64,6 71,4 40,9 58 64,8 71,4 43,4 58 65 71,7 46,5 58,9 65 71,8 46,8 59 65,2 71,8 47,6 59,2 65,8 72,4 48,2 59,5 65,9 72,5 50 60,1 66,1 72,6 50,4 60,2 66,5 72,9 50,5 60,4 66,7 73,2 51,5 60,5 66,9 73,3 52 60,7 67 74 53 61 67,4 74 53,1 61 67,9 74,1 53,2 61,6 68 74,3 53,6 62 68,1 74,5 53,8 62 68,4 74,5 54,3 62,2 68,9 74,6 54,7 62,8 69,6 74,6 55 63,4 69,9 75 55,3 63,8 70 75,6 55,7 64,2 70,5 75,7 56,1 64,4 70,6 75,8 56,3 64,5 70,9 76,1 Categoria Bajo peso Normal Alto Total fi 76,5 77,3 77,3 77,4 77,5 77,9 78 78,5 81,5 82,2 82,4 83,2 84,5 84,5 87,4 88,7 89 89,8 89,8 89,9 92,1 92,4 94,4 95,9 96 hi 58 75 17 150 hi% 0,39 0,50 0,11 1,00 38,67% 50,00% 11,33% 100,00% CORRELACIÒN DE DOS VARIABLES CUANTITATIVAS 1.- Los siguientes datos representan la conductividad térmica del cloruro de metilo a las temperaturas (°C). Grafique Conductividad f (TºC) Calcule las constantes a, b, r y r2 Con los valores calculados de r y r2 diga qué relación existe entre las dos variables (fuerte, positiva, negativa etc) Y: Conductividad 0,115 0,123 0,135 0,149 0,163 0,173 0,189 0,202 X: temperatura 10 37,7 65,5 93,3 121,1 148,8 176,6 204,4 N 1 2 3 4 5 6 7 8 TOTAL media x 107,175 X: temperatura 10 37,7 65,5 93,3 121,1 148,8 176,6 204,4 857,4 Y: Conductividad 0,115 0,123 0,135 0,149 0,163 0,173 0,189 0,202 1,249 Xi-X -97,18 -69,48 -41,68 -13,88 13,93 41,63 69,43 97,23 Yi-Y -0,041125 -0,033125 -0,021125 -0,007125 0,006875 0,016875 0,032875 0,045875 (Xi-X)^2 9442,98 4826,78 1736,81 192,52 193,91 1732,64 4819,83 9452,70 32398,16 (Yi-Y)^2 0,00169127 0,00109727 0,00044627 5,0766E-05 4,7266E-05 0,00028477 0,00108077 0,00210452 0,00680288 media y 0,156125 Conductividad f (TºC) 0,25 0,2 0,15 0,1 0,05 0 0 𝑎= 50 100 150 ∑[(𝑥𝑖 − 𝑥̅ ) × (𝑦𝑖 − 𝑦̅)] 14,8176 = = 0,00045736 ∑(𝑥𝑖 − 𝑥̅ )2 32398,16 𝑏 = 𝑦̅ − 𝑎 × 𝑥̅ = 0,156125 − 0,00045736 × 107,175 = 0,107107426 𝑟= ∑[(𝑥𝑖 − 𝑥̅ ) × (𝑦𝑖 − 𝑦̅)] 𝑆𝑥𝑦 14,8176 = = = 0,998095769 𝑆𝑥 × 𝑆𝑦 √∑(𝑥𝑖 − 𝑥̅ )2 × √∑(𝑦𝑖 − 𝑦̅)2 √32398,16 × √0,00680288 ŷ=ax+b 0,11168103 0,1243499 0,13706452 0,14977913 0,16249374 0,17516262 0,18787723 0,20059184 TOTAL 𝑟2 = ŷ -Y -0,04444397 -0,0317751 -0,01906048 -0,00634587 0,00636874 0,01903762 0,03175223 0,04446684 (ŷ -Y)^2 0,00197527 0,00100966 0,0003633 4,027E-05 4,0561E-05 0,00036243 0,0010082 0,0019773 0,00677699 𝑆̂𝑦 ∑(𝑦̂𝑖 − 𝑦̅)2 0,00677699 = = = 0,996195164 → 99,6195164 % 𝑆𝑦 ∑(𝑦𝑖 − 𝑦̅)2 0,00680288 La variable Y es influida en un 99,61% por la variable X 200 250 (Xi-X)*(Yi-Y) 3,99632188 2,30135938 0,88038438 0,09885938 0,09573437 0,70242187 2,28234688 4,46019688 14,817625 2.- La determinación de níquel en aceites vegetales hidrogenados se puede realizar calcinando la muestra a cenizas, añadiendo molibdeno como patrón interno y analizando por espectroscopia de emisión. Se prepara las solucione estándares que se indica en la tabla, Grafique Intensidad f (Concentración) Calcule las constantes a, b, r y r2 Con los valores calculados de r y r2 diga qué relación existe entre las dos variables (fuerte, positiva, negativa etc) Intensidad 0,43 0,7 0,9 1,15 1,34 Ni (ppm) 0,2 0,4 0,6 0,8 1 Intensidad f (Concentración) 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 0 N 1 2 3 4 5 TOTAL 0,2 0,4 0,6 0,8 1 X: Ni (ppm) Y: Intensidad Xi-X Yi-Y (Xi-X)^2 (Yi-Y)^2 (Xi-X)*(Yi-Y) ŷ =ax+b ŷ -Y (ŷ -Y)^2 0,2 0,43 -0,4 -0,474 0,16 0,22468 0,1896 0,45 -0,454 0,206116 0,4 0,7 -0,2 -0,204 0,04 0,04162 0,0408 0,677 -0,227 0,051529 0,6 0,9 0 -0,004 0 1,6E-05 0 0,904 0 0 0,8 1,15 0,2 0,246 0,04 0,06052 0,0492 1,131 0,227 0,051529 1 1,34 0,4 0,436 0,16 0,1901 0,1744 1,358 0,454 0,206116 3 4,52 0,4 0,51692 0,454 TOTAL 0,51529 media x media y 0,6 0,904 a b r r^2 1,2 1,135 0,223 0,99842211 99,68% La variable Y es influida en un 99,68% por la variable X 3.- Se prepara una serie de soluciones estándares de plata cada una por quintuplicado (tabla) Grafique Intensidad f (Concentración) Calcule las constantes a, b, r y r2 Con los valores calculados de r y r2 diga qué relación existe entre las dos variables (fuerte, positiva, negativa etc) Concentración en (mg/ml) Intensidad de fluoresceína n1 n2 n3 n4 n5 0 4 3 4 5 4 10 22 20 21 22 21 20 44 46 45 44 44 FUNCIÒN DENSIDAD DE PROBABILIDAD 1.- Con los siguientes datos realice la prueba de normalidad de a) KOLMOGOROV – SMIRNOF 30 60 63 60 63 63 40 75 81 79 78 77 50 104 109 107 101 105 66,7 75,6 57,0 60,2 65,0 53,6 62,2 68,4 71,4 71,4 64,5 65,7 82,2 77,5 70,5 89,8 60,1 66,9 58,9 32,0 51,5 64,4 52,0 61,6 59,5 Peso en kg 94,4 78,5 77,4 35,6 71,7 34,5 53,1 40,0 40,9 28,1 72,4 65,8 53,8 55,9 29,6 29,0 82,4 24,5 63,2 17,8 74,1 34,5 22,5 36,0 63,4 29,0 58,0 74,5 62,0 81,5 53,0 56,3 59,2 25,0 29,4 76,5 72,9 67,0 18,7 17,8 70,9 61,0 69,9 25,0 60,4 66,5 75,7 50,0 64,2 74,6 50,5 67,4 46,8 48,2 65,9 57,4 74,0 23,4 68,1 74,0 68,9 77,9 71,8 70,0 55,3 62,8 71,4 23,3 32,9 70,6 69,8 25,8 72,5 64,8 64,6 Media Desviación estándar Mínimo Máximo Rango Número de datos Número de intervalos sturges Raíz número de datos Tamaño del intervalo Intervalos 1 2 3 4 5 6 7 8 9 10 Lim. Inferior 17,8 25,46 33,12 40,78 48,44 56,1 63,76 71,42 79,08 86,74 57,648 18,315443 17,8 94,4 76,6 100 7,6 10 7,66 Lim. Superior 25,46 33,12 40,78 48,44 56,1 63,76 71,42 79,08 86,74 94,4 fi 9 8 5 3 10 17 26 17 3 2 100 Estimador Kolmogorov Smirnov = 0,079746848 0,079746848 > 0.05 Por lo tanto no sigue una distribución normal 2.- Con los siguientes datos realice la prueba de normalidad de a) SHAPIRO WILK b) Diagrama Q-Q (percentil en x, percentil de Y) Peso Kg 60,7 60,5 32,6 66,1 65,0 46,5 37,3 73,2 50,4 75,8 72,6 62,0 62,4 58,0 xi 21,63 29,29 36,95 44,61 52,27 59,93 67,59 75,25 82,91 90,57 hi 0,09 0,08 0,05 0,03 0,1 0,17 0,26 0,17 0,03 0,02 hi A 0,09 0,17 0,22 0,25 0,35 0,52 0,78 0,95 0,98 1 hrE 0,0394 0,0903 0,1785 0,3076 0,4663 0,6307 0,7740 0,8790 0,9439 0,9776 hi A - hrE 0,0506 0,0797 0,0415 -0,0576 -0,1163 -0,1107 0,0060 0,0710 0,0361 0,0224 74,5 84,5 40,0 59,0 54,3 55,0 64,6 61,0 19,5 53,2 56,7 54,7 68,0 74,6 74,3 22,1 a) N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Peso Kg (Xi) 19,5 22,1 32,6 37,3 40 46,5 50,4 53,2 54,3 54,7 55 56,7 58 59 60,5 60,7 61 62 62,4 64,6 65 66,1 68 72,6 73,2 74,3 74,5 74,6 75,8 84,5 media (Xi-media)^2 ai*Dif SW c (Xi-media)^2 1479,9409 1286,6569 643,6369 427,2489 322,9209 131,5609 57,3049 22,7529 13,4689 10,6929 8,8209 1,6129 0,0009 1,0609 6,4009 7,4529 9,1809 16,2409 19,6249 43,9569 49,4209 66,0969 100,6009 214,0369 231,9529 266,6689 273,2409 276,5569 317,9089 703,8409 57,97 7010,863 -80,8927 0,93335639 SW (0.967) = 0.05 SW(0,93335639) < SW (0.967) Por lo tanto sigue una distribución normal b) Peso Kg 32,6 37,3 40 46,5 54,3 55 59 60,5 60,7 61 64,6 65 66,1 74,5 84,5 19,5 22,1 50,4 53,2 54,7 56,7 58 62 62,4 68 72,6 73,2 74,3 74,6 75,8 ai 0,4254 0,2944 0,2487 0,2148 0,187 0,163 0,1415 0,1219 0,1036 0,0862 0,0697 0,0537 0,0381 0,0227 0,0076 Xi inv 84,5 75,8 74,6 74,5 74,3 73,2 72,6 68 66,1 65 64,6 62,4 62 61 60,7 60,5 59 58 56,7 55 54,7 54,3 53,2 50,4 46,5 40 37,3 32,6 22,1 19,5 Dif (Xi - Xi inv) -65 -53,7 -42 -37,2 -34,3 -26,7 -22,2 -14,8 -11,8 -10,3 -9,6 -5,7 -4 -2 -0,2 Diagrama Q-Q 100 90 y = 1,1337x - 6,6192 80 70 60 50 40 30 20 10 0 0 10 20 30 40 50 La mayoría de pares ordenados siguen una tendencia lineal 60 70 80 90