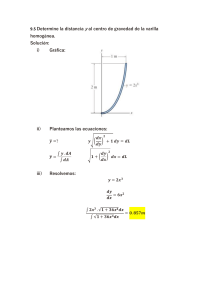
UNAP UNIVERSIDAD NACIONAL DEL ALTIPLANO PUNO FACULTAD DE INGENIERÍA MECÁNICA ELÉCTRICA, ELECTRÓNICA Y SISTEMAS ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS CURSO: MATEMÁTICA BASICA DOCENTE: LIC. OLANDA VELAZQUES BERTHA PRESENTADO POR: ARACAYO MAMANI, JHON MARCO CASTRO CCALLO, VANESSA YHOSELIN CENTENO CCORIMANYA, JHON ALEX PACCORI LOPEZ, PAUL ANDDY PORTO CALAMANI, ALAIN EDY ZAMATA CHURA, MELVIN ELIZALDE PUNO – PERÚ 2022 TRABAJO DE FUNCIONES, MATRICES Y SISTEMAS DE ECUACIONES FUNCIONES 1. 𝑓: ℝ ⟶ ℝ es la función afín definida por 𝑓(𝑥) = 𝑎𝑥 + 𝑏 𝑠𝑖 𝑓(3) = 1 𝑦 𝑓(−3) = 6 hallar 𝑓(𝑥). 𝑓 (3) = 3𝑎 + 𝑏 = 1 & 𝑓 (−3) = −3𝑎 + 𝑏 = 6 Reemplazando las funciones 𝟑𝒂 + 𝒃 + (−𝟑𝒂) + 𝒃 = 𝟏 + 𝟔 Sumamos las funciones 𝑓(3) y 𝑓(−3) 𝟑𝒂 − 𝟑𝒂 + 𝒃 + 𝒃 = 𝟕 Resolvemos la ecuación 𝟏 𝟏 𝟐𝒃 𝟐 = 𝟕 × 𝟐 Igualamos 𝟕 𝒃=𝟐 Hallamos una variable…(b) 𝑓 (3) = 3𝑎 + 𝑏 = 1 Remplazamos la variable (b) 7 7 7 3𝑎 + 2 − 2 = 1 − 2 5 3𝑎 = − 2 Resolvemos la ecuación Igualamos 1 5 1 3 2 3 3𝑎 × = − × 5 Resolvemos 𝑎 = −6 Hallamos la variable…(a) 𝑓(𝑥) = 𝑎𝑥 + 𝑏 Reemplazamos las variables 5 7 𝑓 (𝑥 ) = − 6 𝑥 + 2 la función queda así Solución 2. Si 𝑓(𝑥) = −4𝑥 2 − 4𝑥 + 5 . Hallar el punto donde la función alcanza una máxima altura 𝑦 = −4𝑥 2 − 4𝑥 + 5 𝑥= −(−4) Aplicamos la formula del vértice para hallar las 2(−4) coordenadas x 4 𝑥 = −8 Simplificamos 1 𝑥 = −2 Coordenada del punto x… (1) 𝑦 = −4𝑥 2 − 4𝑥 + 5 Reemplazamos la variable por la coordenada hallada 1 1 𝑦 = −4(− 2)2 − 4(− 2) + 5 1 1 Resolvemos, eliminamos cuadrados 𝑦 = −4(4) − 4(− 2) + 5 Resolvemos, aplicamos ley de signos 𝑦 = −1 + 2 + 5 Sumamos y restamos 𝑦=6 Coordenada del punto 𝒚… (2) 𝟏 El punto de altura máxima es en el punto 𝒙 = − 𝟐 ∧ 𝒚 = 𝟔 3. Halle el rango y gráfica de la función 𝑓(𝑥) = 𝑥𝑒 −𝑥 𝑦 = 𝑥𝑒 −𝑥 Despejar los exponentes 1 𝑦 = 𝑥 𝑒𝑥 La función tiene una expresión indefinida −∞; ∞) siendo 𝑦|𝑦 𝜖 R Rango ( 4. Halle el dominio, rango y gráfica de la función 𝑓(𝑥) = √4 − 𝑥. 𝐷𝑜𝑚 𝑓(𝑥) = √4 − 𝑥 4−𝑥 ≥0 4 ≥ 𝑥 = 𝐷𝑜𝑚 < −∞, 4] 𝑅𝑎𝑛 𝑓(𝑥) = √4 − 𝑥 𝑦 = √4 − 𝑥 𝑐√𝑎𝑥 + 𝑏 + 𝑘 ⇒ 𝑓(𝑥) ≥ 0 𝑦 ≥ 0 = 𝑅𝑎𝑛 [0, +∞ > Gráfica 5. Determinar el rango y trazar la gráfica de la siguiente función 𝑓(𝑥) = |2𝑥 − 1| + |𝑥 − 2|. 𝐷𝑜𝑚 𝑓 (𝑥 ) = |2𝑥 − 1| + |𝑥 − 2| 𝑥≥0 ⋁ 𝑥<0 𝐷𝑜𝑚 ℝ 𝑅𝑎𝑛 𝑓(𝑥) = |2𝑥 − 1| + |𝑥 − 2| 2𝑥 − 1 ≥ 0 𝑦 − (2𝑥 − 1) < 0 𝑥< 1 1 , ≤ 𝑥 < 2, 𝑥 ≥ 2 2 2 Rango de los intervalos 1 3 −∞ < 𝑥 < ; < 𝑓 (𝑥 ) < +∞ 2 2 𝑥 − 2 ≥ 0 𝑦 − (2𝑥 − 1) < 0 1 3 ≤ 𝑥 < 2; ≤ 𝑓(𝑥) < 3 2 2 3 2 ≤ 𝑥 < +∞; ≤ 𝑓 (𝑥 ) < +∞ 2 3 3 𝑓 (𝑥 ) ≥ = 𝑅𝑎𝑛 [ , +∞ > 2 2 Gráfica 6. Halle el dominio y la gráfica de la función 𝑓(𝑥) = 4 + √𝑥 − 2 𝐷𝑜𝑚 𝑓 (𝑥 ) = 4 + √𝑥 − 2 𝑥−2≥0 𝑥 ≥ 2 = 𝐷𝑜𝑚 [2, +∞ > 𝑅𝑎𝑛 𝑓(𝑥) = 4 + √𝑥 − 2 𝑦 = 4 + √𝑥 − 2 𝑦 ≥ 4 = 𝑅𝑎𝑛 [4, +∞ > Gráfica 𝑐√𝑎𝑥 + 𝑏 + 𝑘 ⇒ 𝑓(𝑥) ≥ 0 7. Determine (𝑓 ∘ 𝑔)(𝑥) 𝑦 (𝑔 ∘ 𝑓 )(𝑥 ) ,𝑓(𝑥) = correspondientes dominios (𝑓 ∘ 𝑔)(𝑥) 𝑥+1 , 𝑔(𝑥) = √𝑥 4 𝑥+1 𝑓(√𝑥) = 4 𝑓(𝑥) = √𝑥 + 1 4 𝐷𝑜𝑚: (𝑓 ∘ 𝑔)(𝑥 ) (𝑓 ∘ 𝑔)(𝑥 ) = 𝑥≥0 ∴ 𝐷𝑜𝑚 [0; 𝛼 > (𝑔 ∘ 𝑓 )(𝑥 ) 𝑔( 𝑥+1 ) = √𝑥 4 (𝑔 ∘ 𝑓 )(𝑥 ) = √ 𝑥+1 4 𝑥+1 4 , 𝑔(𝑥) = √𝑥 y sus 𝐷𝑜𝑚; (𝑔 ∘ 𝑓 )(𝑥 ) 𝑥+1 ≥0 4 4(𝑥 + 1) ≥ 0 ∴ 𝐷𝑜𝑚 [−1; 𝛼 > 8. (Curva de aprendizaje) La eficiencia de un individuo para realizar una tarea rutinaria mejora con la práctica. Sea 𝑡 el tiempo que empleó en el aprendizaje de la tarea y 𝑦 una medida del rendimiento del individuo. (Por ejemplo, y podría ser el número de veces, por hora, que la tarea puede realizarse). Entonces una función que con frecuencia se utiliza para relacionar y con t es 𝑦 = 𝐴(1 − 𝑒 −𝑘𝑡 ) donde A y k son constantes. (La gráfica de tal relación entre 𝑦 y t se denomina curva de aprendizaje). Después de una hora de práctica, una persona, en una línea de ensamblado puede apretar 10 tuercas en 5 minutos. Después de 2 horas, la persona puede apretar 15 tuercas en 5 minutos. Determine las constantes A y k. ¿Cuántas tuercas puede apretar la persona después de 4 horas de práctica? 𝑦 = 𝐴(1 − 𝑒 −𝑘𝑡 ) 𝑟𝑒𝑒𝑚𝑝𝑙𝑎𝑠𝑎𝑚𝑜𝑠: 𝑎) … . . 10 = 𝐴(1 − 𝑒−𝑘1 ) . Después de 2 horas, la persona puede apretar 15 tuercas en 5 minutos 𝑏) … … . 15 = 𝐴(1 − 𝑒−𝑘2) 𝑙𝑢𝑒𝑔𝑜 𝑑𝑖𝑣𝑖𝑑𝑖𝑚𝑜𝑠 10 𝐴(1 − 𝑒−𝑘1) = 15 𝐴(1 − 𝑒−𝑘2) 2 (1 − 𝑒−𝑘1) = 3 (1 − 𝑒−𝑘2) 𝑎 𝑏 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑚𝑜𝑠 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑒𝑛 𝑎𝑠𝑝𝑎 2(1 − 𝑒−𝑘2 ) = 3(1 − 𝑒−𝑘1) 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑣𝑎 2 − 2𝑒−𝑘2 = 3 − 3𝑒−𝑘1 0 = 2(𝑒 −𝑘 2 ) − 3𝑒−𝑘1 + 1 … . 𝑟𝑒𝑠𝑜𝑙𝑣𝑒𝑚𝑜𝑠 𝑙𝑎 𝑒𝑐𝑢𝑎𝑠𝑖𝑜𝑛 𝑒 −𝑘 = 𝑒 −𝑘 𝐶𝑎𝑚𝑏𝑖𝑎𝑜 𝑑𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 2(𝑒 −𝑘 2 ) − 3𝑒−𝑘1 + 1 = 0 2(𝑒 −𝑘 ) − 1 (𝑒 −𝑘 ) − 1 2𝑒−𝑘 − 1 = 0 𝑦 𝑒−𝑘 − 1 = 0 2𝑒−𝑘 − 1 = 0 𝑒 −𝑘 = 1 2 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑎 𝑙𝑜𝑠 𝑑𝑜𝑠 𝑙𝑎𝑑𝑜𝑠 𝑐𝑜𝑛 log 𝑒 log 𝑒 𝑒−𝑘 = log 𝑒 −𝑘 = ln 1 2 𝑘 = − ln 1 2 1 2 𝑒 −𝑘 − 1 = 0 𝑒 −𝑘 = 1 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑎 𝑙𝑜𝑠 𝑑𝑜𝑠 𝑙𝑎𝑑𝑜𝑠 𝑐𝑜𝑛 log 𝑒 log 𝑒 𝑒−𝑘 = log 𝑒 1 −𝑘 = 0 𝑘=0 hallemos A sabiendo 1 𝑒 −𝑘 = 𝑒𝑛 𝑙𝑎 𝑒𝑐𝑢𝑎𝑐𝑖𝑜𝑛 𝑎 2 𝑝𝑟𝑜𝑝𝑖𝑒𝑑𝑎𝑑: log 𝑒 𝑁 = ln 𝑁 10 = 𝐴(1 − 𝑒−𝑘1) 1 10 = 𝐴 (1 − ) 2 𝐴 = 20 ¿Cuántas tuercas puede apretar la persona después de 4 horas de práctica? 1 Sabiendo A=20 y 𝑒 −𝑘 = 2 𝑦 = 𝐴(1 − 𝑒 −𝑘𝑡 ) 𝑦 = 𝐴(1 − 𝑒 −𝑘4 ) 𝑦 = 20 (1 − 𝑦= 14 ) 2 20(15) 16 𝑦= 75 4 9. . (Crecimiento de ventas) Un producto nuevo fue introducido en el mercado en t= 0, y a partir de ese momento sus ventas mensuales crecieron de acuerdo con la fórmula 𝑆 = 4000(1 − 𝑒 −𝑘𝑡 )3 Si S=2000 cuando t=10 (esto es, después de 10 meses), determine el valor de k. Solución: 𝑆 = 4000(1 − 𝑒 −𝑘𝑡 )3 S=2000 t=10 Teniendo las condiciones iniciales, procederemos a buscar el valor de k. 2000 = 4000(1 − 𝑒 −𝑘(10) )3 1 = (1 − 𝑒 −𝑘(10) )3 2 1 √ = 1 − 𝑒 −𝑘(10) 2 3 1 √ − 1 = −𝑒 −𝑘(10) 2 3 −0,79 + 1 = 𝑒 −𝑘(10) ln 0,21 = ln 𝑒 −𝑘(10) −1.56 = −10𝑘 𝑘 = 0.16 10. Radiactividad Una sustancia radiactiva decae de acuerdo con la fórmula donde N es el número de miligramos presentes después de t horas. 𝑁 = 10𝑒 −0.041𝑡 (a) Determine la cantidad inicial. (b) Al décimo de miligramos más cercano, determine la cantidad presente después de 2 horas, (c) después de 10 horas. (d) A la décima de hora más cercana, determine la vida media de la sustancia, y (e) el número de horas para que quede un miligramo. Solución: (a) Determine la cantidad inicial. No es la cantidad inicial y corresponde a t=0 𝑁𝑜 = 10𝑒 −0.041(0) 𝑁𝑜 = 10𝑒 0 𝑁𝑜 = 10 𝑚𝑔 (b) Al décimo de miligramos más cercano, determine la cantidad presente después de 2 horas. t = 2 horas 𝑁 = 10𝑒 −0.041(2) 𝑁 = 10𝑒 −0.82 𝑁 = 10(0.45) 𝑁 = 4.5 𝑚𝑔 Por consiguiente, en forma aproximada, 4,5 miligramos estas presentes después de 2 horas. (c) Después de 10 horas t = 10 horas 𝑁 = 10𝑒 −0.041(10) 𝑁 = 10𝑒 −4.1 𝑁 = 10(0.017) 𝑁 = 0.17 𝑚𝑔 Por consiguiente, en forma aproximada, 0.17 miligramos estas presentes después de 10 horas. (d) A la décima de hora más cercana, determine la vida media de la sustancia. 𝑁𝑜 = 10𝑒 −0.041𝑡 2 No = 10 Reemplazamos: 10 = 10𝑒 −0.041𝑡 2 5 = 10𝑒 −0.041𝑡 1 = 𝑒 −0.041𝑡 2 1 ln = ln 𝑒 −0.041𝑡 2 −0.69 = −0.041𝑡 𝑡 = 1.7 La vida media aproximadamente 1.7 horas. (e) El número de horas para que quede un milagro. N=1 Reemplazamos: 1 = 10𝑒 −0.041𝑡 1 = 𝑒 −0.041𝑡 10 1 ln = ln 𝑒 −0.041𝑡 10 −2.3 = −0.041𝑡 𝑡 = 5.6 Por consiguiente, 1 miligramo está presente después de 5,6 horas. MATRICES 11. Hallar la matriz inversa −𝟏 𝑨=[ 𝟓 𝟏 𝟓 −𝟖 −𝟏 −𝟐 𝟑] 𝟑 F1 −𝟏 𝑨 = F2 [ 𝟓 F3 𝟏 𝟓 −𝟖 −𝟏 −𝟐 𝟏 𝟑 𝟎 𝟑 𝟎 −𝟏 1 F1 + F2 [ 𝟎 5 F1 + F3 𝟎 𝟓 𝟏𝟕 𝟓 𝟒 −𝟐 𝟏 𝟕 𝟏 − 𝟓 𝟏 𝟏 𝟓 −𝟐 𝟏 𝟏𝟕 𝟕 𝟏 − 𝟓 𝟓 𝟒 𝟏 𝟏 F1 −𝟏 F2 [ 𝟎 F3 𝟎 −𝟏 𝟒F2 − 𝟎 𝟏𝟕 F3 𝟓 [𝟎 𝟗F1 − 𝟐F3 −𝟗 𝟕 𝟗F2 − F3 𝟎 𝟓 𝟎 [ 𝟏𝟓𝟑 − F − 𝟒𝟓F2 𝟓 1 𝟏𝟑𝟕𝟕 𝟓 𝟎 [ 𝟎 𝟎 𝟏 𝟎 𝟓 𝟏𝟕 𝟓 𝟎 𝟎 𝟏 𝟓 𝟎 𝟎 𝟎] 𝟏 𝟎 𝟏 𝟓 𝟎 𝟎 𝟎] 𝟏 𝟎 𝟎] 𝟏 𝟏 𝟎 𝟎 −𝟐 𝟏 𝟕 𝟏 𝟎 𝟓 − 𝟓 𝟑 𝟒 𝟏𝟕 −𝟗 − ] 𝟓 𝟓 𝟓 𝟑𝟗 𝟖 𝟑𝟒 − 𝟒𝟓 𝟎 𝟓 𝟓 𝟓 𝟐𝟎𝟒 𝟏𝟕 𝟏𝟏𝟗 𝟏𝟓𝟑 𝟎 𝟐𝟓 𝟐𝟓 𝟐𝟓 𝟓 𝟑 𝟒 𝟏𝟕 𝟎 −𝟗 − 𝟓 𝟓 𝟓 ] 𝟎 𝟎 𝟏𝟓𝟑 𝟓 𝟎 𝟎 −𝟗 𝟑𝟐𝟏𝟑 𝟏𝟗𝟖𝟗 𝟏𝟓𝟑 − − 𝟐𝟓 𝟐𝟓 𝟐𝟓 𝟐𝟎𝟒 𝟏𝟕 𝟏𝟏𝟗 𝟐𝟓 𝟐𝟓 𝟐𝟓 𝟑 𝟒 𝟏𝟕 − ] 𝟓 𝟓 𝟓 − 5𝐹1 𝟏𝟑𝟕𝟕 1377 − 𝟓 5𝐹2 153 𝟎 1𝐹3 𝟎 − 9 [ − 𝟎 𝟎 𝟏𝟓𝟑 𝟓 𝟎 𝟎 5𝐹1 1377 5𝐹2 𝟏 𝟎 153 𝟎 1𝐹3 − 9 [ 𝟑𝟐𝟏𝟑 𝟏𝟗𝟖𝟗 𝟏𝟓𝟑 − − 𝟐𝟓 𝟐𝟓 𝟐𝟓 𝟐𝟎𝟒 𝟏𝟕 𝟏𝟏𝟗 𝟐𝟓 𝟐𝟓 𝟐𝟓 𝟑 𝟒 𝟏𝟕 − ] 𝟓 𝟓 𝟓 − −𝟗 𝟕 𝟏𝟑 𝟏𝟓 𝟒𝟓 𝟎 𝟒 𝟏 𝟎 𝟒𝟓 𝟏 𝟏𝟓 𝟑 𝟒 − − 𝟏𝟓 𝟒𝟓 − 𝟎 𝟏 𝟎 𝟎. 𝟒𝟕 𝑨−𝟏 = [ 𝟎. 𝟐𝟕 −𝟎. 𝟎𝟕 𝟎. 𝟐𝟗 𝟎. 𝟎𝟐 −𝟎. 𝟎𝟗 𝟏 𝟒𝟓 𝟕 𝟒𝟓 𝟏𝟕 𝟒𝟓] 𝟎. 𝟎𝟐 𝟎. 𝟏𝟔 ] 𝟎. 𝟑𝟖 12. Hallar el determinante de la matriz 𝟑 𝑨 = [𝟔 𝟏 𝟔 𝟕 −𝟒 −𝟐 𝟐] 𝟑 𝟑 𝟔 −𝟐 𝟔 𝟕 𝟐 𝟏 −𝟒 𝟑 = (𝟔𝟑 + 𝟒𝟖 + 𝟏𝟐) = 𝟏𝟐𝟑 𝟑 𝟔 −𝟐 [𝟔 𝟕 𝟐 ] 𝟑 𝟔 −𝟐 𝟔 𝟕 𝟐 𝟏 −𝟒 𝟑 = (𝟏𝟎𝟖 − 𝟐𝟒 − 𝟏𝟒) = 𝟕𝟎 𝟑 𝟔 −𝟐 [𝟔 𝟕 𝟐 ] 𝟑 [𝟔 𝟏 𝟔 𝟕 −𝟒 −𝟐 𝟐 ] = 𝟏𝟐𝟑 − 𝟕𝟎 = 𝟓𝟑 𝟑 𝟑 |𝑨| = [𝟔 𝟏 𝟔 𝟕 −𝟒 −𝟐 𝟐 ] = 𝟓𝟑 𝟑 SISTEMA DE ECUACIONES 13. Resolver el siguiente sistema de ecuaciones utilizando el método de Gauss Jordan 1x 3 y 7 z 0 2 x 4 y 5z 0 4 x 6 y 8z 0 Se acomodan los coeficientes y los resultados en una matriz: 1 3 7 ⋮0 [2 4 −5 ⋮ 0] 4 −6 8 ⋮ 0 Buscando la matriz identidad, restamos la fila 3 por 2 veces la fila 2: 1 3 [2 4 4 −6 7 ⋮0 1 3 7 𝑓 −2𝑓2 [ 2 4 −5 −5 ⋮ 0] 3 ⟶ 8 ⋮0 4 − 4 −6 − 8 8 + 10 ⋮0 ⋮ 0] ⋮0 Restamos la fila 2 por 2 veces la fila 1: 1 [2 0 3 4 −14 7 ⋮0 1 3 𝑓2 −2𝑓1 [2 − 2 4 − 6 −5 ⋮ 0] ⟶ 18 ⋮ 0 0 −14 7 ⋮0 −5 − 14 ⋮ 0] 18 ⋮0 Restamos la fila 3 por 7 veces la fila 2: 1 [0 0 3 −2 −14 7 −19 18 ⋮0 1 3 7 𝑓 −7𝑓2 [0 −2 −19 ⋮ 0] 3 ⟶ ⋮0 0 −14 + 14 18 + 133 ⋮0 ⋮ 0] ⋮0 Dividimos la fila 3 por 151: 1 3 [0 −2 0 0 7 −19 151 1 3 ⋮ 0 𝑓3 0 −2 ⋮ 0] 151 [ ⋮0 ⟶ 0 0 7 −19 151 151 ⋮0 ⋮ 0] ⋮0 Restamos la fila 1 por 7 veces la fila 3: 1 [0 0 3 7 −2 −19 0 1 ⋮0 1 𝑓 − 7𝑓3 [0 ⋮ 0] 1 ⟶ ⋮0 0 3 7−7 −2 −19 0 1 ⋮0 ⋮ 0] ⋮0 Sumamos la fila 2 por 19 veces la fila 3: 1 [0 0 3 0 −2 −19 0 1 ⋮0 1 3 𝑓2 + 19𝑓3 [0 −2 ⋮ 0] ⟶ ⋮0 0 0 0 −19 + 19 1 Sumamos la fila 1 por 3/2 la fila 2: ⋮0 ⋮ 0] ⋮0 1 [0 0 3 0 −2 0 0 1 3(−2) ⋮0 3 1 3+ 2 ⋮ 0] 𝑓1 + 2 𝑓2 [ 0 −2 ⟶ ⋮0 0 0 0 ⋮0 ⋮ 0] 0 ⋮0 1 Dividimos la fila 2 por 2 negativo para hallar finalmente la matriz identidad: 1 1 0 0 ⋮ 0 𝑓2 [0 −2 0 ⋮ 0] −2 [0 0 0 1 ⋮0 ⟶ 0 0 0 −2 0 −2 0 1 ⋮0 1 ⋮ 0] = [0 ⋮0 0 0 0 1 0 0 1 ⋮0 ⋮ 0] ⋮0 ∴𝑥=0 ∴𝑦=0 ∴𝑧=0 14. Para que valores de 𝑎 el sistema de ecuaciones lineales tiene solución única, infinitas soluciones, no tiene solución. 3𝑥 𝑥 2𝑥 3 −2 [1 −8 2 1 3 [0 2 3 0 [0 −2 22 − 3 7 3 −2 22 − 3 1 1 5 𝑎 +𝑧 = 3 +5𝑧 = 8 +𝑎 𝑧 = −1 3 ⋮3 1 1(3) ⋮ 8 ] 𝑓2 − 3 𝑓1 [1 − 3 ⟶ ⋮ −1 2 3 1 14 3 𝑎 1 14 3 3𝑎 − 2 3 −2𝑦 −8𝑦 +𝑦 ⋮ 3 2 ⋮ 7 ] 𝑓3 − 3 𝑓1 ⟶ ⋮ −1 0 2(3) 2 − [ 3 −2 1(−2) −8 − 3 1 1 1(1) 5− 3 𝑎 −2 22 − 3 2(−2) 1− 3 1 14 3 2(1) 𝑎− 3 ⋮3 1(3) ] ⋮8− 3 ⋮ −1 ⋮ ⋮ 3 7 2(3) ⋮ −1 − 3 ] 3 −2 1 22 14 ⋮ 3 7 0 − 3 3 ⋮ 7 𝑓3 + 22 𝑓2 7 7 22 3𝑎 − 2 7 14 ⟶ ⋮ −3 0 + (− ) + ( ) ] [ 3 22 3 3 22 3 7 22 7 + (− ) = 0 3 22 3 11 3𝑎 − 2 7 14 33𝑎 − 22 + 49 3 11𝑎 + 9 ( ) +( ) = =( ) 11 3 3 22 33 3 11 −3 + 3 −2 22 0 − 3 [0 0 7(7) −66 + 49 17 = =− 22 22 22 1 14 3 11𝑎 + 9 11 3𝑥 − 2𝑦 + 1𝑧 = 3 ⋮ 3 22𝑦 14𝑧 ⋮ 7 − + =7 = 3 3 17 11𝑎 + 9 17 ⋮− 22] 𝑧=− 11 22 ⋮ 3 ⋮ 7 7(7) ⋮ −3 + 22 ]