Deduccion de las Ecuaciones de Navier Stokes

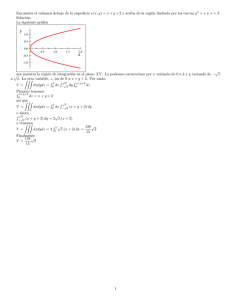
DEDUCCIÓN DE LAS ECUACIONES DE NAVIER STOKES
Introducción
Uno de los campos de la física más complicados de estudiar son los fluidos, el
comportamiento de gases y líquidos en movimiento. Comprender, por ejemplo, los
flujos de aire turbulento o los remolinos que se forman cuando el agua discurre por
una tubería o la sangre por una arteria son de suma importancia, tanto para la
ingeniería como para la medicina.
Las ecuaciones que rigen la dinámica de fluidos son las conocidas como ecuaciones
de Navier-Stokes, producto del francés constructor de puentes Claude-Louis Navier
y del matemá-tico irlandés George Stokes. El primero en obtener estas ecuaciones
fue el francés en una época (1822) en que no se comprendía muy bien cuál era la
física de la situación que estaba matematizando. De hecho, lo único que hizo fue
modificar unas ecuaciones ya existentes y obtenidas por el famoso matemático
Euler, de modo que incluyesen las fuerzas existentes entre las moléculas del fluido.
Aproximadamente 20 años después, Stokes justificó las ecuaciones del ingeniero
francés deduciéndolas adecuadamente. A pesar de que las ecuaciones de NavierStokes son sólo una aproximación del comportamiento real de los fluidos, se utilizan
para estudiar cualquier aspecto que tenga que ver con éstos; el problema es que si
uno estudia el movimiento de un fluido con estas ecuaciones, es incapaz de prever
si ese movimiento se va a mantener siempre o se va a complicar.
Ecuaciones de Navier Stokes
La segunda ley de Newton establece que la rapidez de cambio de momentum de
una partícula de fluido es igual a la suma de las fuerzas que están actuando sobre el
fluido.
Rapidez de incremento
De momentum de una
Partícula de fluido
=
Suma de las fuerzas que están actuando
sobre la partícula del fluido.
Clasificándose las fuerzas en:
Fuerzas Superficiales: la fuerza causada por la diferencia de presiones, la fuerza de
viscosidad, la tensión superficial.
Fuerzas Volumétricas: La fuerza de gravedad, la fuerza centrifuga, la fuerza coriolis
y la fuerza electromagnética.
Por lo que de acuerdo a la segunda ley de newton:
m . a = fza. presion + fza.vis cos idad + W + Sm
(1)
para el movimiento de un fluido la tensión superficial juega un papel poco importante
siendo por ese motivo que no se toma en cuenta, Sm es todas las demas fuerzas
volumétricas que podrían estar afectando el movimiento del fluido bajo una condición
dada.
utilizando el punto de vista lagrangiano, la velocidad “V” (y por tanto sus
componentes vx, vy, y vz) en cada punto del fluido dependerá del punto de que se
trate y del tiempo que se considere matemáticamente:
v x = f 1 ( x, y , z , t )
v y = f 2 ( x, y , z , t )
v z = f 3 ( x, y , z , t )
En un instante “t” determinado estas ecuaciones nos dan la velocidad del fluido en
cada punto del espacio, es decir la configuración del flujo en ese instante; mientras
que en un punto determinado (x, y, z) las mismas ecuaciones nos dan la variación
de la velocidad con el tiempo en ese punto. Se tiene por tanto.
∂v x
∂v
∂v
∂v
dt + x dx + x dy + x dz
∂t
∂x
∂y
∂z
∂v y
∂v y
∂v y
∂v y
dv y =
dt +
dx +
dy +
dz
∂t
∂x
∂y
∂z
∂v
∂v
∂v
∂v
dv z = z dt + z dx + z dy + z dz
∂t
∂x
∂y
∂z
dv x =
(2a)
(2b)
(2c)
y dividendo los dos miembros de las 3 ecuaciones anteriores por dt se tiene:
dv x ∂v x ∂v x
∂v
∂v
=
+
vx + x v y + x vz
dt
∂t
∂x
∂y
∂z
dv y ∂v y ∂v y
∂v y
∂v y
=
+
vx +
vy +
vz
dt
∂t
∂x
∂y
∂z
dv z ∂v z ∂v z
∂v
∂v
=
+
vx + z v y + z vz
dt
∂t
∂x
∂y
∂z
Ya que:
dx
= vx ,
dt
dy
= vy, ,
dt
dz
= vz
dt
Ahora sabemos que:
dv x
= ax ,
dt
dv y
dt
= a y, ,
dv z
= az
dt
(3a)
(3b)
(3c)
Por lo que:
∂vx ∂vx
∂v
∂v
+
vx + x v y + x vz
∂t
∂x
∂y
∂z
∂v ∂v
∂v
∂v
a y = y + y vx + y v y + y vz
∂t
∂x
∂y
∂z
∂v ∂v
∂v
∂v
az = z + z vx + z v y + z vz
∂t
∂x
∂y
∂z
ax =
(4a)
(4b)
(4c)
Consideremos ahora la siguiente figura, donde el punto A(x, y, z) se encuentra en el
centro del elemento del fluido con un volumen dx, dy, dz .
Figura 1. Componentes de la presión en la dirección x
Sea p = f ( x, y, z ) la presión en el punto A. Sobre las 6 caras del cubo actúa la
fuerza debida a la presión por claridad en la figura solamente se han indicado las
fuerzas debidas a la presión que actúan sobre las caras normales al eje x.
La presión en la cara vertical izquierda será:
∂p dx
p + dp = p −
∂x 2
y en la cara vertical derecha
∂p dx
p + dp = p +
∂x 2
ahora realizando la suma para obtener el diferencial de presión en la dirección x
(p −
∂p dx ⎛
∂p dx ⎞
∂p
) − ⎜ p −
⎟ = − dx
∂x 2
∂x 2 ⎠
∂x
⎝
y sabiendo que la fuerza es igual a la presión por el área. Por lo que la fuerza que
esta actuando en la dirección x debida a la presión es igual:
∂p
dxdydz
∂x
∂p
p y = − dxdydz
∂y
∂p
pz = − dxdydz
∂z
px = −
(5a)
(5b)
(5c)
el peso del fluido en este caso solamente actúa sobre el eje z siendo este la masa
del fluido contenida en el cubo por la aceleración de la gravedad:
dW = − ρ dxdydz g
El estado de los esfuerzos sobre un elemento de un fluido es definido en términos de
la presión y las nueve componentes de los esfuerzos viscosos los cuales se
muestran en la figura siguiente, los esfuerzos viscosos son indicados por τ. La
notación de los subíndices τij es aplicado para indicar la dirección de los esfuerzos
viscosos. Los subíndice i y j indican que la componente del esfuerzo actúa en la
dirección j sobre una superficie normal a la dirección i. Ahora para obtener una
fuerza viscosa por unidad de volumen, considérese el elemento de fluido con
volumen dx, dy, dz . Por el momento si solo se toman los esfuerzos viscosos que
actúan en la dirección x. Por lo que la fuerza en la dirección x es la suma de las
componentes de los esfuerzos actuando en esa dirección sobre el elemento del
fluido.
Figura 2. componentes de los esfuerzos en la dirección x
Por lo que el esfuerzo que esta actuando en las caras E,W es igual
(τ xx +
∂τ xx 1
∂τ 1 ⎞ ∂τ
⎛
dx ) − ⎜τ xx − xx dx ⎟ = xx dx
∂x 2
∂x 2 ⎠
∂x
⎝
en las caras N,S es:
(τ yx +
∂τ yx 1
∂τ yx 1 ⎞ ∂τ yx
⎛
dy ) − ⎜⎜τ yx −
dy ⎟ =
dy
∂y 2
∂y 2 ⎟⎠
∂y
⎝
y finalmente en las caras T,B:
(τ zx +
∂τ zx 1
∂τ 1 ⎞ ∂τ
⎛
dz ) − ⎜τ zx − zx dz ⎟ = zx dz
∂z 2
∂z 2 ⎠
∂z
⎝
pero si la fuerza es igual a la presión por el área, entonces la fuerza que esta
actuando sobre el elemento del fluido en la dirección x esta dada por:
∂τ yx
∂τ xx
∂τ
dxdydz +
dydxdz + zx dzdydx
∂x
∂y
∂z
∂τ xy
∂τ yy
∂τ zy
fx =
dxdydz +
dydxdz +
dzdydx
∂x
∂y
∂z
∂τ yz
∂τ
∂τ
f z = xz dxdydz +
dydxdz + zz dzdydx
∂x
∂y
∂z
fx =
en la dirección x
(6a)
en la dirección y
(6b)
en la dirección z (6c).
recordando la ecuación establecida de acuerdo con la segunda ley de Newton
m . a = fza. presion + fza.vis cos idad + W + Sm
poniendo las componentes de cada fuerza para la dirección x y sabiendo que el
diferencial de masa contenido en el volumen del fluido es igual:
dw = ρ dxdydz
(ρ dxdydz )⎛⎜⎜ ∂v x
∂v x
∂v
∂v
⎞ ⎛ ∂p
⎞
v x + x v y + x v z ⎟⎟ = ⎜ − dxdydz ⎟ + (− ρ dxdydz g ) +
∂x
∂y
∂z ⎠ ⎝ ∂x
⎠
⎝ ∂t
+
⎛ ∂τ xx ∂τ yx ∂τ zx ⎞
⎜⎜
⎟⎟dxdydz + SM x dxdydz
+
+
∂
x
∂
y
∂
z
⎝
⎠
+
dividendo ambas partes de la ecuación entre el volumen diferencial (dxdydz) la
ecuación anterior nos queda:
∂τ yx ∂τ zx ⎞
⎛ ∂τ
∂v
∂v
⎛ ∂v x ∂v x
⎞
∂p
⎟⎟ + SM x eje x
+
v x + x v y + x v z ⎟⎟ = − − ρg x + ⎜⎜ xx +
+
∂x
∂y
∂z ⎠
∂x
∂
x
∂
y
∂
z
⎝ ∂t
⎝
⎠
∂
v
∂
v
∂
v
∂
v
∂
τ
∂
τ
∂
τ
⎛ y
⎞
⎛ xy
∂p
y
y
y
yy
zy ⎞
⎟ + SM y eje y
ρ ⎜⎜
+
vx +
vy +
v z ⎟⎟ = − − ρg y + ⎜⎜
+
+
∂x
∂y
∂z ⎠
∂y
∂y
∂z ⎟⎠
⎝ ∂t
⎝ ∂x
ρ ⎜⎜
∂τ yz ∂τ zz ⎞
⎛ ∂τ
⎛ ∂v z ∂v z
⎞
∂v
∂v
∂p
⎟ + SM z eje z
+
v x + z v y + z v z ⎟⎟ = − − ρg z + ⎜⎜ xz +
+
∂x
∂y
∂z ⎠
∂z
∂y
∂z ⎟⎠
⎝ ∂t
⎝ ∂x
ρ ⎜⎜
Esfuerzo Viscoso
Ahora se determinará el esfuerzo viscoso que surge del movimiento cortante.
Considérese primero el flujo cortante más simple que resulte posible, que es áquel
entre dos planos paralelos según se muestra en la figura 3(a) . un elemento del
fluido se deforma cuando la superficie superior se desliza respecto de su superficie
inferior. Para un fluido newtoniano, en las superficies inferior y superior de un
elemento de fluido se genera un esfuerzo cortante proporcionalmente al gradiente de
velocidad y la viscosidad del fluido:
τ xy = µ
∂u x
∂y
pero debe existir un esfuerzo complementario τ yx en las caras verticales del
elemento de la figura 3(b) que es igual a τ xy , pues de lo contrario el movimiento de
rotación del elemento sufriría una aceleración con una velocidad angular infinita al
hacerse su tamaño infinitesimal. Una relación así debe cumplirse para cualquier
dirección de los ejes como lo ejemplifica la figura 3(c):
τ xy = τ yx ;
τ yz = τ zy ;
τ xz = τ zx
(a)
(b)
(c)
Figura 3. El movimiento de corte mas sencillo de (a) da origen a los esfuerzos
viscosos cortantes τxy y τyx que se muestran en (b). Si dicho movimiento esta en
dirección y, los esfuerzos viscosos cortantes son los de (c)
Ahora considérese un flujo cortante en el cual las placas que lo limitan están
orientadas en la dirección y. El esfuerzo cortante τxy en la superficie de este
elemento es:
τ yx = µ
∂v y
∂x
= τ xy
cualquier combinación de los flujos que describe la figura 3(b) y (c) origina esfuerzos
viscosos que son simplemente la suma de cada unas de estas contribuciones por
separado:
τ xy = τ yx = µ
∂v y
∂v y ⎞
⎛ ∂v
∂v x
⎟⎟
+µ
= µ ⎜⎜ x +
∂y
∂x
∂
y
∂
x
⎝
⎠
Este resultado es válido para el movimiento cortante o tangencial en el plano x, y de
la figura 3. También deben cumplirse relaciones parecidas en los planos y,z y z,x.
En un fluido newtoniano los esfuerzos viscosos son proporcional a la deformación.
La tridimensional forma de la ley de viscosidad de newton para flujos comprensibles
envuelve dos constantes de proporcionalidad: la µ, que es la viscosidad dinámica
relativa a las deformaciones lineales por los esfuerzos y λ, que es una viscosidad
relativa a la deformación volumétrica. Los nueve componentes de los esfuerzos
viscosos, de las cuales 6 son independientes, que son:
⎛ ∂v
∂v ⎞
⎛ ∂v
y
⎟;
τ xy = τ yx = µ ⎜⎜ x +
∂x ⎟⎠
⎝ ∂y
∂v ⎞
τ yz = τ zy = µ ⎜⎜ x + z ⎟⎟;
∂y ⎠
⎝ ∂z
⎛ ∂v z ∂v x ⎞
+
⎟
∂z ⎠
⎝ ∂x
τ zx = τ xz = µ ⎜
los otros 3 son los componentes normales a la superficie del fluido, de los cuales el
esfuerzo τxx actua en un plano normal al eje x y esta dado por:
" ∂v % " ∂v ∂v ∂v %
τ xx == 2µ $ x ' + λ $ x + y + z '
# ∂x & # ∂x ∂y ∂z &
no mucho se conoce acerca de la segunda viscosidad porque su efecto es pequeño
en la practica. Sin embargo para los gases una buena aproximación puede ser
obtenida tomando el valor de λ = -2/3 µ , el termino que acompaña a λ es la
deformación volumétrica que esta dada por el divergente de la velocidad. Para los
líquidos los cuales son incompresibles la deformación volumétrica es cero y estos 3
esfuerzos viscosos se definen por:
⎛ ∂v x ⎞
⎟;
⎝ ∂x ⎠
τ xx = 2µ ⎜
⎛ ∂v y
⎝ ∂y
τ yy = 2µ ⎜⎜
⎞
⎟⎟;
⎠
⎛ ∂v z ⎞
⎟
⎝ ∂z ⎠
τ zz = 2µ ⎜
volviendo a la ecuación en la dirección x y sustituyendo el valor de los esfuerzos
viscosos por su correspondiente:
ρa x = −
∂v y ⎞ ∂ ⎛ ∂v x ∂v z ⎞
⎞ ∂ ⎛ ∂v
∂p
∂ ⎛ ⎛ ∂v ⎞ 3
⎟ + µ ⎜
⎟ + SM x
− ρg x + ⎜⎜ 2µ ⎜ x ⎟ − ∇.V ⎟⎟ + µ ⎜⎜ x +
+
∂x
∂x ⎝ ⎝ ∂x ⎠ 2
∂x ⎟⎠ ∂z ⎜⎝ ∂z
∂y ⎟⎠
⎠ ∂y ⎝ ∂y
poniendo el valor de ax nos da la ecuación de Navier Stokes para el eje x en su
forma general y siguiendo lo mismo obtenemos para los demás ejes (y,z)
⎛ ∂vx ∂vx
⎞
⎞
∂v
∂v
∂p
∂ ⎛ ⎛ ∂v ⎞ 3
+
vx + x v y + x vz ⎟⎟ = − − ρg x + ⎜⎜ 2µ ⎜ x ⎟ − ∇.V ⎟⎟ +
∂x
∂y
∂z ⎠
∂x
∂x ⎝ ⎝ ∂x ⎠ 2
⎠
⎝ ∂t
∂ ⎛ ∂vx ∂v y ⎞ ∂ ⎛ ∂vx ∂vz ⎞
⎟ + µ ⎜
⎟ + SM x
µ ⎜
+
+
Para la dirección x
∂y ⎜⎝ ∂y ∂x ⎟⎠ ∂z ⎜⎝ ∂z ∂y ⎟⎠
ρ ⎜⎜
∂v
∂v
⎛ ∂v y ∂v y
⎞
∂v ⎞
∂p
∂ ⎛ ∂v
+
v x + y v y + y v z ⎟⎟ = − − ρg y + µ ⎜⎜ y + x ⎟⎟ +
∂x
∂y
∂z ⎠
∂y
∂x ⎝ ∂x ∂y ⎠
⎝ ∂t
⎞
∂ ⎛ ⎛ ∂v y ⎞ 3
∂ ⎛ ∂v ∂v ⎞
⎜ 2 µ ⎜⎜
⎟ + + µ ⎜⎜ x + z ⎟⎟ + SM y Para la dirección y
⎟
−
∇
.
V
⎟
⎜
⎟
∂y ⎝ ⎝ ∂y ⎠ 2
∂z ⎝ ∂z ∂y ⎠
⎠
(7a)
ρ ⎜⎜
(7b)
⎛ ∂v z ∂v z
⎞
∂v
∂v
∂v ⎞
∂p
∂ ⎛ ∂v
+
v x + z v y + z v z ⎟⎟ = −
− ρg z + µ ⎜ x + z ⎟ +
∂x
∂y
∂z ⎠
∂z
∂x ⎝ ∂z
∂x ⎠
⎝ ∂t
⎞
∂ ⎛ ∂v z ∂v x ⎞ ∂ ⎛⎜ ⎛ ∂v y ⎞ 3
⎜⎜
⎟⎟ − ∇.V ⎟ + SM z
⎟⎟ +
µ ⎜⎜
+
2
µ
Para la dirección z (7c)
⎟
∂y ⎝ ∂y
∂z ⎠ ∂y ⎜⎝ ⎝ ∂y ⎠ 2
⎠
ρ ⎜⎜
para el caso de un fluido incomprensible con viscosidad constante y si ∇.V=0 las
ecuaciones de Navier stokes se simplifican de la siguiente manera:
en la dirección x:
∂v
∂v
∂v
⎛ ∂v
⎞
∂p
∂ ⎛ ⎛ ∂v
ρ ⎜⎜ x + x v x + x v y + x v z ⎟⎟ = − − ρg x + ⎜⎜ 2µ ⎜ x
∂x
∂y
∂z ⎠
∂x
∂x ⎝ ⎝ ∂x
⎝ ∂t
∂ ⎛ ∂v x ∂v z
µ ⎜
+
∂z ⎜⎝ ∂z
∂y
⎞ ⎞ ∂ ⎛ ∂v x ∂v y ⎞
⎟ +
+
⎟ ⎟⎟ + µ ⎜⎜
∂x ⎟⎠
⎠ ⎠ ∂y ⎝ ∂y
⎞
⎟⎟ + SM x
⎠
⎛ ∂ 2v ∂ 2v ∂ 2v ⎞
⎛ ∂vx ∂vx
∂v
∂v ⎞
∂p
∂ ⎛ ∂v ∂v ∂v ⎞
+
vx + x v y + x vz ⎟⎟ = − − ρg x + µ ⎜⎜ 2x + 2x + 2x ⎟⎟ + µ ⎜⎜ x + y + z + ⎟⎟
∂x
∂y
∂z ⎠
∂x
∂y
∂z ⎠
∂x ⎝ ∂x ∂y ∂z ⎠
⎝ ∂t
⎝ ∂x
ρ ⎜⎜
∂v
∂v
⎛ ∂v x ∂v x
⎞
∂p
∂
+
v x + x v y + x v z ⎟⎟ = − − ρg x + µ∇ 2 v x + µ (∇.V ) + SM x ; en la direc. x
∂x
∂y
∂z ⎠
∂x
∂x
⎝ ∂t
ρ ⎜⎜
entonces las ecuaciones de Navier Stokes en su forma simplificada quedarían:
∂v
∂v
⎛ ∂v x ∂v x
⎞
∂p
+
v x + x v y + x v z ⎟⎟ = − − ρg x + µ∇ 2 v x + SM x ; para la dirección x
∂x
∂y
∂z ⎠
∂x
⎝ ∂t
ρ ⎜⎜
∂v y
∂v y ⎞
⎛ ∂v y ∂v y
∂p
+
vx +
vy +
v z ⎟⎟ = − − ρgy + µ∇ 2 v y + SM y ; para la dirección y
∂x
∂y
∂z ⎠
∂y
⎝ ∂t
⎛ ∂v
⎞
∂v
∂v
∂v
∂p
ρ ⎜⎜ z + z v x + z v y + z v z ⎟⎟ = − − ρg z + µ∇ 2 v z + SM z ; para la dirección x
∂x
∂y
∂z ⎠
∂z
⎝ ∂t
ρ ⎜⎜