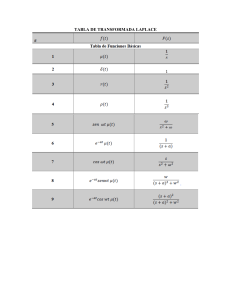
TRANSFORMADA DE LAPLACE DEFINICION Dada una función f(t), su Transformada de Laplace, denotada por F(s) o £[f(t)], se define como: Donde s es una variable compleja dada por s = σ + j ω La Transformada de Laplace es una transformación integral de una función f(t) del dominio del tiempo al dominio de la frecuencia compleja, lo que da por resultado F(s). TRANSFORMADA DE LAPLACE Características • Es una integral impropia ya que el límite superior es infinito (∞). • El límite inferior de la integral es cero o sea que la Transformada de Laplace no tiene en cuenta los valores de f(t) para valores negativos de t y se le denomina Transformada de Laplace de un solo lado o unilateral. TRANSFORMADA DE LAPLACE Características • f(t) tiene una discontinuidad finita en el origen. • Si el límite inferior es 0 ─ se incluye la discontinuidad. • Si el límite inferior es 0+ se excluye la discontinuidad. Para el análisis de circuitos eléctricos discontinuidad). se escoge 0 ─ (incluir la TRANSFORMADA DE LAPLACE Tipos de Transformada de Laplace Transformada funcional: es la Transformada de Laplace de una función especifica. TRANSFORMADA DE LAPLACE Tipos de Transformada de Laplace Transformada funcional: es la Transformada de Laplace de una función especifica.