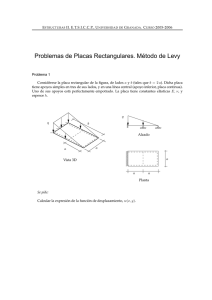
PRÀCTICA 6: Transport de calor per convecció forçada Arnau Forcadell Artiga Victor Canela Sánchez Andreu Ferraté Moreno Alex Garcia Manzanares Grup 33 2n de GEQ 5 de desembre de 2018 Resultats Qualificació global: Bloc 1 (5P) ________________________________________________________________________ 1.- Ompliu la taula següent per expressar les mesures i resultats dels experiments que heu realitzat (adjunteula en forma d'imatge). En l’encapçalament ha de figurar el tipus de placa, posició de la placa, temperatura ambient, temperatura de la superfície de la placa, potència calorífica subministrada, velocitat del ventilador i les temperatures mesurades en l’espiga o l’aleta pels casos de les superfícies esteses (2P). Tipus de placa Posició Ta (ºC) Ts (ºC) Q (W) u (ventilador) (m/s) T (superfície estesa) (ºC) Plana Vertical 23.7 43 5.5 0.59 - Cilindres Vertical 23.8 36 11.3 0.54 30.1 Aletes Vertical 23.6 37 12.6 0.56 29.6 Aletes Vertical 23.7 36 13.2 1.12 28.3 Aletes Vertical 23.5 40 20.6 1.15 32.7 Aletes Vertical 23.8 43 20.6 0.57 33.7 Heu de realitzar les mesures suficients per poder observar l'efecte independent de les diferents variables (potència de l'escalfador, velocitat del ventilador i tipus de superfície) en la transferència de calor. Q: 2.- Plantegeu el balanç macroscòpic d'energia del sistema aire-placa en estat estacionari pel cas de la placa d'aletes. Empleneu la taula (només les files que calguin) i calculeu l'error (2P). El balanç macroscòpic d’energia seria: 𝑄𝑒𝑛𝑡𝑟𝑎 = 𝑄𝑠𝑢𝑟𝑡 On Qentra és la potència subministrada per la font d’alimentació a la placa y Q surt és la potència que és absorbida per l’aire. La Qentra és una dada que ens ofereix la font d’alimentació, mentre que, per conèixer la potència absorbida per l’aire s’ha realitzat el següent càlcul. 𝑄 = 𝑚𝑎𝑖𝑟𝑒 ∗ 𝐶𝑝𝑎𝑖𝑟𝑒 ∗ ∆𝑇 m és la massa d’aire en Kg/s, calculada a partir de la velocitat (m/s) oferta per l’anemòmetre y la secció de la canonada (m2), juntament amb la densitat (Kg/m3) trobada a la bibliografia[1]. La Cp (J/Kg·K) és la capacitat calorífica de l’aire a la temperatura mitja de treball (aprox. 25ºC), segons bibliografia. I ∆𝑇 (K) és la diferencia de la temperatura de l’aire abans i després d’absorbir calor. ҪENGEL, Yunus A. y John M. CIMBALA, “Mecánica de fluidos: Fundamentos y aplicaciones”, 1ª edición, McGraw-Hill, 2006. Tabla A-9. [1] Q dissipada per la placa* (W) Q absorbida per l'aire (W) Diferència (W) Error (%) 5.5 6.6 1.1 18.2 11.3 11.7 0.4 3.6 12.6 14.3 1.7 12.7 13.2 16.7 3.5 23.6 20.6 25.8 5.2 22.5 20.6 18.8 1.8 9.0 *Q dissipada per la placa = potència de l'escalfador Durant la realització de la pràctica es modificà la potència subministrada a la placa, es per això que la Q dissipada varia. Anoteu la superfície de la placa d'aletes: S = 0,218m2 Per al càlcul s’ha tingut en compte que l’àrea útil per a la transferència de calor és aquella que està en contacte amb l’aire, per tant, a la base de la placa s’ha de sostraure la superfície ocupada per la base de les aletes. A les aletes, no s’ha de tenir en compte tampoc l’àrea de la base i a més s’ha restat l’àrea dels orificis que tenien algunes aletes. Q: 3.- A partir de les observacions realitzades, feu l'anàlisi de la influència de les diferents variables en el transport convectiu de calor. És a dir, expliqueu si millora o empitjora la transferència de calor segons si augmentem la potència de l'escalfador, la velocitat de l'aire i segons el tipus de superfície (1P). Potència: El resultat d’augmentar la potencia del escalfador es que la placa assolirà una major temperatura i, per tant, la Q absorbida per l’aire serà major, ja que, aquesta transferència d’energia depèn directament de la diferencia de temperatures entre l’aire que entra i la placa. Velocitat de l’aire: Si s’augmenta la velocitat de l’aire també augmentarà la massa de fluid capaç d’absorbir calor y per tant la calor absorbida augmentarà. Tipus de superfície: El tipus de superfície també es una variable important, si s’augmenta l’àrea de contacte entre la placa i l’aire també augmentarà la calor cedida per aquesta, com hem vist durant la realització de la pràctica al laboratori. La geometria també es important però en aplicacions s’hauria de tenir en compte la pèrdua de càrrega degut a la resistència al pas del fluid. Q: Bloc 2 (3P) ________________________________________________________________________ 4.- Calculeu el coeficient de transferència de calor h en el cas de la placa plana, utilitzant (1P). l'equació (1) 𝑄̇ = 𝐴 ∗ ℎ ∗ (𝑇1 − 𝑇2 ) ℎ= ℎ= 0.011 𝑄̇ 𝐴 ∗ (𝑇1 − 𝑇2 ) 6.599 𝑊 ∗ (43 − 23.7)º𝐶 𝑚2 h = 31,1 W·m-2·K-1 Q: 5.-Consulteu fonts bibliogràfiques per obtenir valors típics de h aplicables i compareu-los amb experimentalment (0.5P). l'obtingut El valor bibliogràfic trobat fa referència a gasos amb convecció forçada: h =25-500[2] W·m-2·K-1 bib [2] http://www.e-uned.es/covers/506.pdf. Pag.35 El valor obtingut durant la realització de la pràctica s’apropa al predit per la bibliografia, la diferencia entre els dos valors es pot deure a errors experimentals i a les condicions de treball, ja que diferencies en algunes variables com la velocitat del flux i al règim d’aquest poden modificar bastant el resultat del coeficient de transferència de calor. Q: 6.-Amb el valor del coeficient de transferència obtingut h, calculeu Nu. Calculeu també els Prandtl (Pr) i Reynolds (Re) en el cas de la placa plana (0.5P). números de Per al càlcul de Nu s’ha fet servir la relació següent: 𝑁𝑢 = ℎ∗𝐿 𝑘 On ℎ es el coeficient de transferència de calor per convecció que s’ha trobat experimentalment (W/m 2·K), 𝐿 es l’amplada de la placa (m) i 𝑘 la conductivitat tèrmica de l’aire a 25ºC. Nu =121,9 Per al càlcul del número de Prandtl s’ha tingut en compte la següent relació: 𝑃𝑟 = 𝑣·𝑘 ℎ·𝛼·𝐿 On 𝑣 es la viscositat cinemàtica (m2/s), 𝑘 és la conductivitat tèrmica (W/m·K), ℎ coeficient de transferència de calor (W/m2·K), 𝐿 la longitud de la placa en la direcció del flux (m), 𝛼 és la difusivitat tèrmica (m2/s). Pr =5,99·10-3 El nombre de Reynolds s’ha calculat segons la relació: 𝑅𝑒 = ℎ · 𝐿 · 𝑃𝑟 𝑘 Re =0,730 Q: 7.- Cerqueu a la bibliografia correlacions entre Nu, Re, Pr per a la situació experimental de la pràctica, i apliqueu-les per obtenir Nu i posteriorment h a partir de Pr i Re (1P). Correlació trobada a la bibliografia: Els valors per al número de Reynolds i de Prandtl s’han calculat a partir de les propietats del fluid (aire a 25ºC i Patm) segons les relacions obtingudes a la bibliografia, mentre que per al nombre de Nusselt s’ha utilitzat la relació amb Re i Pr, per a Re<5·10 5 i 0,5<Pr<50. Les expressions emprades es troben a continuació: Per al nombre de Reynolds: 𝑅𝑒 = 𝜌·𝐷𝑒𝑞·𝑢 𝜇 𝑅𝑒 = 3,29 · 103 On 𝜌 es la densitat de l’aire, 𝐷𝑒𝑞 es el diàmetre equivalent de la secció del conducte (D eq=4*A/P), 𝑢 és la velocitat del fliud i 𝜇 es la viscositat dinàmica. Per al nombre de Prandtl: 𝑃𝑟 = 𝐶𝑝∗𝜇 𝑘 𝑃𝑟 = 0,730 On 𝐶𝑝 es la capacitat calorífica màssica de l’aire i 𝑘 es la conductivitat térmica de l’aire. Per al nombre de Nusselt, per a convecció forçada, amb Re i Pr obtinguts: 𝑁𝑢 = 0,664 ∗ 𝑅𝑒 1⁄ 2 ∗ 𝑃𝑟 Font bibliogràfica: http://tecno.cruzfierro.com/formularios/conveccion-forzada http://www.valvias.com/numero-de-reynolds.php Valor de Nu a partir de Pr i Re: 34,3 Valor de h a partir de Nu: 8,75 𝑊⁄ 𝑚2 𝐾 1⁄ 3 Compareu els valors experimentals de Nu i h amb els calculats a partir de les correlacions: Els valors obtinguts emprant les correlacions s’allunyen força dels valors que esperaríem obtenir en les condicions en les que hem estat treballant al laboratori, per altra banda els valors que hem trobat seguint les equacions bibliogràfiques si donen uns resultats que serien esperables en aquestes condicions. Es possible que el model bibliogràfic tingui en compte millors aproximacions en les condicions en que es troba el flux. Q: Conclusions (2P) ________________________________________________________________________ Redacteu 6 conclusions sobre la pràctica. 1) S’ha calculat el valor del coeficient de transferència de calor per convecció forçada, el resultat obtingut encaixa amb en trobat experimentalment per a gasos en aquestes condicions. 2) S’han calculat les relacions de Reynolds, Prandtl i Nusselt, els valors obtinguts segons les relacions emprades no corresponen amb els valors esperats segons les relacions trobades a la bibliografia. 3) Segons la geometria i l’àrea d’intercanvi de la placa calefactora l’aire és capaç d’absorbir una major quantitat de calor, a major àrea més eficient és l’absorció de la calor per l’aire. 4) Al augmentar el cabal d’aire per l’interior de conducte augmenta també la quantitat de calor que és capaç d’absorbir. 5) Quant més diferencia de temperatura hi ha entre la placa i el l’aire millor serà la transferència d’energia en forma de calor per convecció. Es pot comprovar quant, durant la realització de la pràctica augmentàvem la potencia de la placa i assolia així mes temperatura. 6) L’error (diferència) que hem observat entre l’energia absorbida per l’aire i la dissipada per la placa oscil·len entre el 3 i el 26%, aquestes diferències poden ser degudes a la dificultat d’aconseguir l’estat estacionari del sistema.