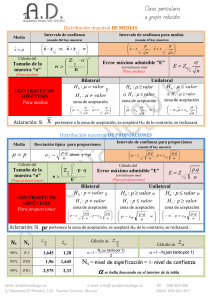
UNIDAD 1 ALUMNO: CATEDRÁTICO: ESPECIALIDAD: MATERIA: PROBABILIDAD Y ESTADISTICA TRABAJO: UNIDAD 1 INDICE INTRODUCCION. UNIDAD 4 INFERENCIA ESTADISTICA. 4.1 ESTIMACION PUNTUAL Y POR INTERVALOS DE CONFIANZA. 4.2 ESTIMACION DE LA MEDIA, DE LA DIFERENCIA DE MEDIAS, DE LA PROPORCION Y DE LA DIFERENCIA DE PROPORCIONES. 4.3 DETERMINACION DEL TAMAÑO DE LA MUESTRA. 4.4 PRUEBA DE HIPOTESIS 4.4.1 PRUEBAS UNILATERALES Y BILATERALES. 4.4.2 PRUEBAS PARA MEDIA Y ARA DIFERENCIA DE MEDIAS. 4.4.3 PRUEBAS PARA PROPORCION Y DIFERENCIA DE PROPORCIONES. 4.5 MUESTRAS PEQUEÑAS. 4.5.1 DISTRIBUCION t DE STUDENT. 4.5.2 DISTRIBUCION DE JI-CUADRADA. CUADROS DE CONTINGENCIA, LIMITACIONES DE LA PRUEBA ………………………………………………………………………1 ………………………………………………………………………3 ……………………………………………………………………..6 …………………………………………………………………….7 ………………………………………………………………….11 ………………………………………………………………….13 ………………………………………………………………….14 ………………………………………………………………….15 ………………………………………………………………….20 ………………………………………………………………….22 ………………………………………………………………….22 ………………………………………………………………..23 INTRODUCCION La inferencia estadística o estadística inferencial es una parte de la Estadística que comprende los métodos y procedimientos para deducir propiedades (hacer inferencias) de una población, a partir de una pequeña parte de la misma (muestra). La Teoría de muestras. La estimación de parámetros. El Contraste de hipótesis. El Diseño experimental. La Inferencia bayesiana. Los métodos no paramétricos 1 Planteamiento del problema Suele iniciarse con una fijación de objetivos o algunas preguntas como ¿cuál será la media de esta población respecto a tal característica?, ¿se parecen estas dos poblaciones? En el planteamiento se definen con precisión la población, la característica a estudiar, las variables, etcétera. Se analizan también en este punto los medios de los que se dispone y el procedimiento. Elaboración de un modelo Se establece un modelo teórico de comportamiento de la variable de estudio. En ocasiones no es posible diseñar el modelo hasta realizar un estudio previo. Los posibles modelos son distribuciones de probabilidad. Extracción de la muestra Se usa alguna técnica de muestreo o un diseño experimental para obtener información de una pequeña parte de la población. Tratamiento de los datos En esta fase se eliminan posibles errores, se depura la muestra, se tabulan los datos y se calculan los valores que serán necesarios en pasos posteriores, como la media muestral, la varianza muestral. Los métodos de esta etapa están definidos por la estadística descriptiva. Estimación de los parámetros Con determinadas técnicas se realiza una predicción sobre cuáles podrían ser los parámetros de la población. Contraste de hipótesis Los contrastes de hipótesis son técnicas que permiten simplificar el modelo matemático bajo análisis. Frecuentemente el contraste de hipótesis recurre al uso de estadísticos muéstrales. Conclusiones Se critica el modelo y se hace un balance. Las conclusiones obtenidas en este punto pueden servir para tomar decisiones o hacer predicciones. El estudio puede comenzar de nuevo a partir de este momento, en un proceso cíclico que permite conocer cada vez mejor la población y características de estudio. 2 UNIDAD 4 INFERENCIA ESTADISTICA La Inferencia Estadística comprende los métodos que son usados para sacar conclusiones de la población en base a una muestra tomada de ella. Incluye los métodos de estimación de parámetros y las pruebas de hipótesis. En la estimación de puntos la idea es hallar un estimado del parámetro poblacional basado en la muestra aleatoria tomada de la población. Uno espera que el estimado este lo mas cerca posible del parámetro. Por ejemplo la media poblacional m. es estimada por la media muestral x . La Estimación de parámetros comprende a su vez la Estimación Puntual, en donde se estudian los diversos métodos de encontrar estimadores y las propiedades óptimas que deben tener éstos, y la Estimación por Intervalos de Confianza, en donde se estima un parámetro usando un intervalo centrado en un estimado del parámetro y de longitud igual a dos veces el error de estimación. El Error de estimación depende del nivel de confianza deseado, usualmente, 90, 95 ó 99 por ciento. Una Hipótesis Estadística es una afirmación que se hace acerca de un parámetro poblacional. Por ejemplo, el tiempo de vida promedio para una persona diagnosticada con cáncer de pulmón es 180 días. El porcentaje de personas que favorecen a un candidato a la presidencia es 60%. 3 La afirmación que está establecida y que se espera sea rechazada después de aplicar una prueba estadística es llamada la hipótesis nula y se representa por Ho. La afirmación que se espera sea aceptada después de aplicar una prueba estadística es llamada la hipótesis alterna y se representa por Ha. Una prueba estadística es una fórmula, basada en la distribución del estimador del parámetro que aparece en la hipótesis y que va a permitir tomar una decisión acerca de aceptar o rechazar una hipótesis nula. Al igual que una prueba de laboratorio para detectar cierta enfermedad, una prueba estadística no es cien por ciento segura y puede llevar a una conclusión errónea. Hay dos tipos de errores que pueden ocurrir. El error tipo I, que se comete cuando se rechaza una hipótesis nula que realmente es cierta y el error tipo II, que se comete cuando se acepta una hipótesis nula que realmente es falsa. Edgar Acuña Capítulo 7 Inferencia Estadística 149 El nivel de significación, representada por a, es la probabilidad de cometer error tipo I, y por lo general se asume que tiene un valor de .05 ó .01.También puede ser interpretado como el área de la región que contiene todos los valores posibles de la prueba estadística donde la hipótesis nula es rechazada. 4 La probabilidad de cometer error tipo II, representado por b y al valor 1-b se le llama la potencia de la prueba. Una buena prueba estadística es aquella que tiene una potencia de prueba alta. En este capítulo, primero se discutirá el cálculo de intervalos de confianza y pruebas de hipótesis para la media poblacional, para una proporción y finalmente para la varianza de una población. Luego se tratará los intervalos de confianza y prueba de hipótesis para la razón de dos varianzas poblacionales, para la diferencia de dos medias poblacionales y por último para la diferencia de dos proporciones. 5 4.1 ESTIMACION PUNTUAL Y POR INTERVALOS DE CONFIANZA. Si a partir de las observaciones de una muestra se calcula un solo valor como estimación de un parámetro de la población desconocido, el procedimiento se denomina estimación p Nos proponemos determinar dos números entre los cuales se halla el parámetro estudiado con cierta certeza. El procedimiento para obtener un intervalo (de confianza) para un parámetro, la media , por ejemplo, requiere de la determinación de un estimador del parámetro y de la distribución del estimador. 6 4.2 ESTIMACION DE LA MEDIA,DE LA DIFERENCIA DE MEDIAS,DE LA PROPORCION Y DE LA DIFERENCIA DE PROPORCIONES Para estimar la media poblacional por medio de intervalos de confianza, será necesario recordar que el Teorema Central del Límite nos daba información de como se hallaban distribuidas las medias muéstrales: "normalmente" con una media igual a la de la población original m (que es la que ahora tratamos de conocer) y desviación típica Supongamos que hemos analizado la muestra ya nombrada de media Km., y que sabemos que la desv. típica de la población es de s=0,4 km., y que nos planteamos estimar la media de todo el instituto, con un nivel de confianza del 95% .El proceso para realizar la estimación es el siguiente: Sabemos por el T.C.L. que las medias muéstrales se distribuyen según La siguiente figura nos ilustrará: Hallamos el valor k de forma que p(-k<Z<k)=0,95 , o lo que es lo mismo p(Z<k)=0,975. Consultando nuestra tabla de la distribución normal, encontraremos que k=1.96 . 7 DIFERENCIA DE MEDIAS Suponga que se tienen dos poblaciones distintas, la primera con media 1 y desviación estándar 1, y la segunda con media 2 y desviación estándar 2. Más aún, se elige una muestra aleatoria de tamaño n1 de la primera población y una muestra independiente aleatoria de tamaño n2 de la segunda población; se calcula la media muestral para cada muestra y la diferencia entre dichas medias. La colección de todas esas diferencias se llama distribución muestral de las diferencias entre medias o la distribución muestral del estadístico La distribución es aproximadamente normal para n130 y n230. Si las poblaciones son normales, entonces la distribución muestral de medias es normal sin importar los tamaños de las muestras. 8 Existen ocasiones en las cuales no estamos interesados en la media de la muestra, sino que queremos investigar la proporción de artículos defectuosos o la proporción de alumnos reprobados en la muestra. La distribución muestral de proporciones es la adecuada para dar respuesta a estas situaciones. Esta distribución se genera de igual manera que la distribución muestral de medias, a excepción de que al extraer las muestras de la población se calcula el estadístico proporción (p=x/n en donde "x" es el número de éxitos u observaciones de interés y "n" el tamaño de la muestra) en lugar del estadísitico media. Una población binomial está estrechamente relacionada con la distribución muestral de proporciones; una población binomial es una colección de éxitos y fracasos, mientras que una distribución muestral de proporciones contiene las posibilidades o proporciones de todos los números posibles de éxitos en un experimento binomial, y como consecuencia de esta relación, las afirmaciones probabilísticas referentes a la proporción muestral pueden evaluarse usando la aproximación normal a la binomial, siempre que np5 y n(1-p) 5. Cualquier evento se puede convertir en una proporción si se divide el número obtenido entre el número de intentos. 9 Distribución Muestral de Diferencia de Proporciones Muchas aplicaciones involucran poblaciones de datos cualitativos que deben compararse utilizando proporciones o porcentajes. A continuación se citan algunos ejemplos: Educación.- ¿Es mayor la proporción de los estudiantes que aprueban matemáticas que las de los que aprueban inglés? Medicina.- ¿Es menor el porcentaje de los usuarios del medicamento A que presentan una reacción adversa que el de los usuarios del fármaco B que también presentan una reacción de ese tipo? Administración.- ¿Hay diferencia entre los porcentajes de hombres y mujeres en posiciones gerenciales. Ingeniería.- ¿Existe diferencia entre la proporción de artículos defectuosos que genera la máquina A a los que genera la máquina B? Cuando el muestreo procede de dos poblaciones binomiales y se trabaja con dos proporciones muéstrales, la distribución muestral de diferencia de proporciones es aproximadamente normal para tamaños de muestra grande (n1p15, n1q15,n2p25 y n2q25). Entonces p1 y p2 tienen distribuciones muéstrales aproximadamente normales, así que su diferencia p1-p2 también tiene una distribución muestral aproximadamente normal. Cuando se estudió a la distribución muestral de proporciones se comprobó que y que , por lo que no es difícil deducir que y que . La fórmula que se utilizará para el calculo de probabilidad del estadístico de diferencia de proporciones es: 10 4.3 DETERMINACION DEL TAMAÑO DE LA MUESTRA Estimar un parámetro determinado con el nivel de confianza deseado. Detectar una determinada diferencia, si realmente existe, entre los grupos de estudio con un mínimo de garantía. Reducir costes o aumentar la rapidez del estudio. Por ejemplo, en un estudio de investigación epidemiológico la determina-ción de un tamaño adecuado de la muestra tendría como objetivo su factibilidad. Así: Si el número de sujetos es insuficiente habría que modificar los criterios de selección, solicitar la colaboración de otros centros o ampliar el perio-do de reclutamiento. Los estudios con tamaños muéstrales insuficientes, no son capaces de detectar diferencias entre grupos, llegando a la conclu-sión errónea de que no existe tal diferencia. Si el número de sujetos es excesivo, el estudio se encarece desde el punto de vista económico y humano. Además es poco ético al someter a más in-dividuos a una intervención que puede ser menos eficaz o incluso perjudicial. El tamaño de una muestra es el número de individuos que contiene. 11 Cálculo del tamaño de la muestra Una fórmula muy extendida que orienta sobre el cálculo del tamaño de la muestra para datos globales es la siguiente: n=((k^2)*N*p*q)/((e^2*(N-1))+((k^2)*p*q)) N: es el tamaño de la población o universo (número total de posibles encuestados). k: es una constante que depende del nivel de confianza que asignemos. El nivel de confianza indica la probabilidad de que los resultados de nuestra investigación sean ciertos: un 95,5 % de confianza es lo mismo que decir que nos podemos equivocar con una probabilidad del 4,5%. Los valores k más utilizados y sus niveles de confianza son: k 1,15 1,28 1,44 1,65 1,96 2 2,58 Nivel de confianza 75% 80% 85% 90% 95% 95,5% 99% (Por tanto si pretendemos obtener un nivel de confianza del 95% necesitamos poner en la fórmula k=1,96) e: es el error muestral deseado. El error muestral es la diferencia que puede haber entre el resultado que obtenemos preguntando a una muestra de la población y el que obtendríamos si preguntáramos al total de ella. Altos niveles de confianza y bajo margen de error no significan que la encuesta sea de mayor confianza o esté más libre de error necesariamente; antes es preciso minimizar la principal fuente de error que tiene lugar en la recogida de datos. 12 4.4 PRUEBA DE HIPOTESIS Las secciones anteriores han mostrado cómo puede estimarse un parámetro a partir de los datos contenidos en una muestra. Puede encontrarse ya sea un sólo número (estimador puntual) o un intervalo de valores posibles (intervalo de confianza). Sin embargo, muchos problemas de ingeniería, ciencia, y administración, requieren que se tome una decisión entre aceptar o rechazar una proposición sobre algún parámetro. Esta proposición recibe el nombre de hipótesis. Este es uno de los aspectos más útiles de la inferencia estadística, puesto que muchos tipos de problemas de toma de decisiones, pruebas o experimentos en el mundo de la ingeniería, pueden formularse como problemas de prueba de hipótesis. Una hipótesis estadistica es una proposición o supuesto sobre los parámetros de una o más poblaciones. 13 4.4.1 PRUEBAS UNILATERALES Y BILATERALES a) Prueba bilateral o de dos extremos: la hipótesis planteada se formula con la igualdad Ejemplo H0 : µ = 200 H1 : µ ≠ 200 b) Pruebas unilateral o de un extremo: la hipótesis planteada se formula con ≥ o ≤ H0 : µ ≥ 200 H0 : µ ≤ 200 H1 : µ < 200 H1 : µ > 200 En las pruebas de hipótesis para la media (μ), cuando se conoce la desviación estándar (σ) poblacional, o cuando el valor de la muestra es grande (30 o más), el valor estadístico de prueba es z y se determina a partir de: El valor estadístico z, para muestra grande y desviación estándar poblacional desconocida se determina por la ecuación: En la prueba para una media poblacional con muestra pequeña y desviación estándar poblacional desconocida se utiliza el valor estadístico t. 14 4.4.2 PRUEBAS PARA MEDIA Y PARA DIFERENCIA DE MEDIAS Pruebas de hipótesis para la media con muestra grande Para realizar una prueba de hipótesis se sigue un procedimiento que quedará mas claro con un ejemplo: El dueño de un café desea saber si la edad promedio de las personas que entran a su negocio es de 20 años, si eso es verdad se piensa realizar una remodelación de dicho café para hacerlo mas juvenil. Para hacer lo anterior se realiza un muestreo aleatorio de 40 personas, dando un promedio de la muestra de 22 años y una desviación estándar de 3.74 años. Paso 1. Determinar la hipótesis Nula “Ho” y Alternativa “Ha”. Ho: La edad promedio de los clientes es de 20 años. Ha: _______________________________________ (El estudiante debe describir la Ha) Nótese que la hipótesis nula considera IGUAL a 20 años por lo tanto es una prueba de hipótesis de dos colas. Paso 2. Determinar el nivel de significancia. Este nivel representa la probabilidad de rechazar una hipótesis nula verdadera, matemáticamente se puede considerar cualquier valor entre cero y uno; pero para estudios de pruebas de hipótesis normalmente está entre 0.05 y 0.1. Este nivel está determinado por el analista y debe basarse en las características del estudio y el riesgo que se considere aceptable de cometer el error tipo I. Nivel de significancia del estudio para el ejemplo: α = 0.1 15 Gráficamente el nivel de significancia se distribuye en la curva de distribución normal tal como se muestra en la figura, nótese que en el caso de pruebas de hipótesis de medias, ésta se ubica en la parte media de la distribución de probabilidad: Paso 3. Calcular los intervalos que implican ese nivel de significancia. Para dicho nivel de significancia los valores de Z son: Z = +/- 1.6448 Quedando de la siguiente manera: Ho: μ = 20 años Ho: μ = 20 años Z = - 1.6448 Z = 1.6448 16 Paso 4. Calcular el “estadístico” de la prueba. El estadístico Z se calcula de la siguiente manera: s = Se calcula la siguiente desviación estándar = Se calcula el valor de Z tipificado μ Promedio considerado por la hipótesis nula. x Media de la muestra tomada. s Desviación estándar de la muestra. n Número de elementos muestreados. x s Desviación estándar tipificada. z Valor de Z tipificado 3.74 17 Paso 5. Determinar si el estadístico cae dentro de la región que hace la Hipótesis nula verdadera. Como podrá notarse, el estadístico esta fuera de la región que hace verdadera la hipótesis nula. Paso 6. Aceptar o rechazar la hipótesis nula. En este caso como el estadístico de la prueba cae fuera de la región que hace verdadera la hipótesis nula, se rechaza y se toma como verdadera la hipótesis alternativa: Ho: La edad promedio de los clientes es de 20 años. (FALSO) Ha: La edad promedio de los clientes No es de 20 años (VERDAD) 18 Prueba para diferencia de proporciones En algunos diseños de investigación, el plan muestral requiere seleccionar dos muestras independientes, calcular las proporciones muestrales y usar la diferencia de las dos proporciones para estimar o probar una diferencia entre las mismas. Las aplicaciones son similares a la diferencia de medias, por ejemplo si dos empresas consultoras ofrecen datos de proporciones de personas que van a votar por el PRI y al hacer dos estudios diferentes salen resultados ligeramente diferentes ¿pero qué tanta diferencia se requiere para que sea estadísticamente significativo? De eso se tratan las pruebas estadísticas de diferencias de proporciones. El estadístico Z para estos casos se calcula de la siguiente manera: 1 ˆp = proporción de la muestra 1. 2 ˆp = proporción de la muestra 2. 1 p = proporción de la población 1. 2 p = proporción de la población 2. 1 n = tamaño de la muestra 1. 2 n = tamaño de la muestra 2. 19 4.4.3 PRUEBAS PARA PROPORCION Y DIFERENCIA DE PROPORCIONES Las pruebas de hipótesis a partir de proporciones se realizan casi en la misma forma utilizada cuando nos referimos a las medias, cuando se cumplen las suposiciones necesarias para cada caso. Pueden utilizarse pruebas unilaterales o bilaterales dependiendo de la situación particular. La proporción de una población Las hipótesis se enuncian de manera similar al caso de la media. Ho: p = p0 H1: p ¹ p0 En caso de que la muestra sea grande n>30, el estadígrafo de prueba es: se distribuye normal estándar. Regla de decisión: se determina de acuerdo a la hipótesis alternativa (si es bilateral o unilateral ), lo cual puedes fácilmente hacerlo auxiliándote de la tabla 4.4.1. En el caso de muestras pequeñas se utiliza la distribución Binomial. No lo abordaremos por ser complicado y poco frecuente su uso. Diferencia entre las proporciones de dos poblaciones La situación más frecuente es suponer que existen diferencias entre las proporciones de dos poblaciones, para ello suelen enunciarse las hipótesis de forma similar al caso de las medias: Ho: p1 = p2 Þ p1 - p2 = 0 H1: p1 ¹ p2 Puede la hipótesis alternativa enunciarse unilateralmente. El estadígrafo de prueba para el caso de muestras independientes: Siendo a1 y a2, el número de sujetos con la característica objeto de estudio en las muestras 1 y 2 respectivamente, es decir, en vez de calcular la varianza para cada muestra, se calcula una p conjunta para ambas muestras bajo el supuesto que no hay diferencias entre ambas proporciones y así se obtiene la varianza conjunta. Recuerda que q = 1-p. Está de más que te diga que este estadígrafo se distribuye normal estándar. La regla de decisión se determina de manera similar a los casos ya vistos anteriormente. El objetivo de la prueba es comparar estas dos proporciones, como estimadores H1: p1 ¹ p2 Recuerda que la H1 también puede plantearse de forma unilateral. 20 Diferencia entre las proporciones de dos poblaciones La situación más frecuente es suponer que existen diferencias entre las proporciones de dos poblaciones, para ello suelen enunciarse las hipótesis de forma similar al caso de las medias: Ho: p1 = p2 Þ p1 - p2 = 0 H1: p1 ¹ p2 Puede la hipótesis alternativa enunciarse unilateralmente. El estadígrafo de prueba para el caso de muestras independientes: donde Siendo a1 y a2, el número de sujetos con la característica objeto de estudio en las muestras 1 y 2 respectivamente, es decir, en vez de calcular la varianza para cada muestra, se calcula una p conjunta para ambas muestras bajo el supuesto que no hay diferencias entre ambas proporciones y así se obtiene la varianza conjunta. Recuerda que q = 1p. Está de más que te diga que este estadígrafo se distribuye normal estándar. La regla de decisión se determina de manera similar a los casos ya vistos anteriormente. El objetivo de la prueba es comparar estas dos proporciones, como estimadores H1: p1 ¹ p2 Recuerda que la H1 también puede plantearse de forma unilateral. 21 4.5 MUESTRAS PEQUEÑAS 4.5.1 DISTRIBUCION t DE STUDENT En probabilidad y estadística, la distribución t (de Student) es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño. Aparece de manera natural al realizar la prueba t de Student para la determinación de las diferencias entre dos medias muéstrales y para la construcción del intervalo de confianza para la diferencia entre las medias de dos poblaciones cuando se desconoce la desviación típica de una población y ésta debe ser estimada a partir de los datos de una muestra. Caracterización La distribución t de Student es la distribución de probabilidad del cociente donde Z tiene una distribución normal de media nula y varianza 1 V tiene una distribución chi-cuadrado con ν grados de libertad Z y V son independientes Si μ es una constante no nula, el cociente es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad μ. 22 4.5.2 DISTRIBUCION JI- CUADRADA.CUADROS DE CONTINGENCIA, LIMITACIONES DE LA PRUEBA. Estadística, la distribución χ² (de Pearson) es una distribución de probabilidad continua con un parámetro k que representa los grados de libertad de la variable aleatoria donde Zi son variables aleatorias normales independientes de media cero y varianza uno. El que la variable aleatoria X tenga esta distribución se representa habitualmente así: . Es conveniente tener en cuenta que la letra griega χ se transcribe al latín como chi y se pronuncia en castellano como ji. Tabla de contingencia En estadística las tablas de contingencia se emplean para registrar y analizar la relación entre dos o más variables, habitualmente de naturaleza cualitativa (nominales u ordinales). Supóngase que se dispone de dos variables, la primera el sexo (hombre o mujer) y la segunda recoge si el individuo es zurdo o diestro. Se ha observado esta pareja de variables en una muestra aleatoria de 100 individuos. Se puede emplear una tabla de contingencia para expresar la relación entre estas dos variables, del siguiente modo: Diestro Zurdo TOTAL Hombre 43 9 52 Mujer 44 4 48 TOTAL 87 13 100 Las cifras en la columna de la derecha y en la fila inferior reciben el nombre de frecuencias marginales y la cifra situada en la esquina inferior derecha es el gran total. La tabla nos permite ver de un vistazo que la proporción de hombres diestros es aproximadamente igual a la proporción de mujeres diestras. Sin embargo, ambas proporciones no son idénticas y la significación estadística de la diferencia entre ellas puede ser evaluada con la prueba χ² de Pearson, supuesto que las cifras de la tabla son una muestra aleatoria de una población. Si la proporción de individuos en cada columna varía entre las diversas filas y viceversa, se dice que existe asociación entre las dos variables. Si no existe asociación se dice que ambas variables son independientes. El grado de asociación entre dos variables se puede evaluar empleando distintos coeficientes: el más simple es el coeficiente phi que se define por φ = √(χ2 / N) donde χ2 se deriva del test de Pearson, y N es el total de observaciones -el gran total-. Φ puede oscilar entre 0 (que indica que no existe asociación entre las variables) e infinito. A diferencia de otras medidas de asociación, el coeficiente Φ de Cramer no está acotado. 23