Particiones de terreno por el método de rumbo fijo

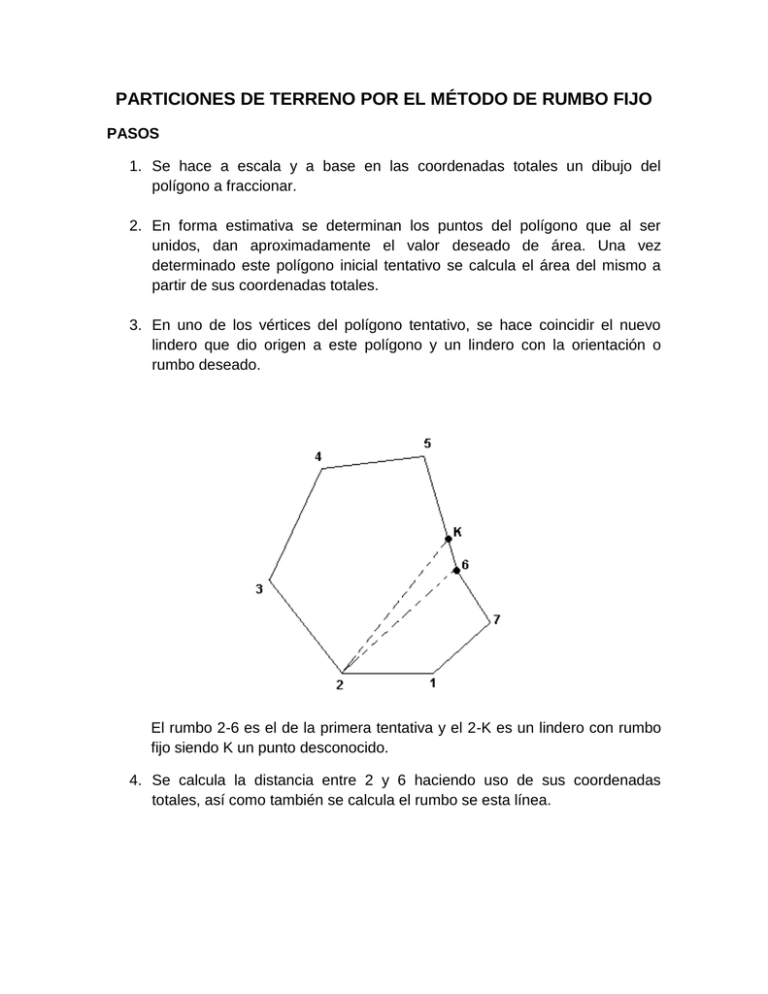
PARTICIONES DE TERRENO POR EL MÉTODO DE RUMBO FIJO
PASOS
1. Se hace a escala y a base en las coordenadas totales un dibujo del
polígono a fraccionar.
2. En forma estimativa se determinan los puntos del polígono que al ser
unidos, dan aproximadamente el valor deseado de área. Una vez
determinado este polígono inicial tentativo se calcula el área del mismo a
partir de sus coordenadas totales.
3. En uno de los vértices del polígono tentativo, se hace coincidir el nuevo
lindero que dio origen a este polígono y un lindero con la orientación o
rumbo deseado.
El rumbo 2-6 es el de la primera tentativa y el 2-K es un lindero con rumbo
fijo siendo K un punto desconocido.
4. Se calcula la distancia entre 2 y 6 haciendo uso de sus coordenadas
totales, así como también se calcula el rumbo se esta línea.
5. Posteriormente se calcula el triángulo 2, K, 6.
Del anterior triángulo se conocen los siguientes elementos:
a. La distancia c que se calculó en el paso 4.
b. El rumbo de la línea K - 6 es dato del polígono por ser el inverso de la 5
– 6.
c. El rumbo 2 – K fue fijado como dato del problema.
d. EL rumbo 2 – 6 también se calculó en el paso 4.
Al conocer los rumbos de las rectas que forman el triángulo, por diferencias
entre ellos se puede hallar fácilmente los valores de los ángulos internos del
triángulo.
Aplicando la ley de senos de la siguiente manera se recopila la información
que se desea:
𝑎
𝑠𝑒𝑛𝛼
𝑏
= 𝑠𝑒𝑛 𝛽
Entonces
𝑠𝑒𝑛𝛼
𝑎 = 𝑐 𝑠𝑒𝑛𝛽
6. Ahora bien, se desea conocer el área del polígono 2, K, 6, 7, 1 que es en
realidad la tentativa a partir de la cual se va a trabajar. Esto quiere decir que
nos resta calcular el área del triángulo 2, K, 6. El valor de esta área es dado
por:
𝐴 (𝑡𝑟𝑖á𝑛𝑔𝑢𝑙𝑜) =
1
2𝑎𝑐𝑆𝑒𝑛𝛽
Otra manera de hallar el área del polígono en mención es que con la
distancia 2 –K y su rumbo se descompone en coordenadas parciales, las
que sumadas a las totales de 2 dan como resultado las coordenadas totales
de K se cuenta con todas la coordenadas del polígono lo cual permite
calcular su área por el método matricial.
7. El área del polígono 1, 2, K, 6, 7 se comparará con el área requerida o
deseada para este caso, la mitad del área total ½(A T). Si este valor es
mayor, el lindero ha de trasladarse hacia el área a desmembrar, si por el
contrario es menor se traslada hacia el resto de la finca matriz.
El problema en realidad consiste en determinar cuánto es necesario
trasladar paralelamente en una dirección perpendicular a su posición
original, asi como la distancia a la que debe de quedar del punto 2 sobre
cualquiera de las dos rectas que llegan a este.
8. Para este caso se supone que el área calculada es menor que el área
requerida por lo que el lindero 2 – K se traslada hacia la parte superior del
polígono a una distancia h.
El área sombreada es la que hay que agregar para obtener el área
requerida, la cual se puede notar claramente que es un trapecio cuyas
bases son m y n y su altura h, teniendo como área ∆A.
9. El trapecio mostrado gurda las siguientes relaciones en sus extremos.
10. En general el trapecio presenta las siguientes relaciones: h = m + b. Pero
esto solo es para este caso particular, hay que analizar cada situación
mediante los rumbos de las líneas ya que tanto a como b pueden tomar
valores positivos o negativos al mismo tiempo o alternándose.
Es decir
h = m + hCotθ – hCotθ.
h = m + h(Cotθ – Cotθ).
Por lo que el área del trapecio o sea A estará dada por la semisuma de las
bases multiplicadas por la altura:
∆𝐴 =
∆𝐴 =
(𝑚 + ℎ)𝑥 ℎ
2
(𝑚 + 𝑚 + 𝑏 − 𝑎)𝑥 ℎ
2
2∆h = (2mh +h2(Cotθ – Cotθ)) x 1/2
Lo cual es una ecuación cuadrática cuya solución está dada por:
−2𝑚 ± √2𝑚2 − 4(𝐶𝑜𝑡𝜃 − 𝐶𝑜𝑡𝜃)(−2∆𝐴)
ℎ=
2(𝐶𝑜𝑡𝜃 − 𝐶𝑜𝑡𝜃)
Para cualquier caso en que sea negativo el valor entre el radical, es un
número imaginario la solución de la ecuación y lo que indica es que los
lados no paralelos del trapecio son convergentes y se interceptan antes de
tener un valor de área igual o mayor al que deseamos. Cuando dichas
líneas son divergentes siempre existe solución para la ecuación anterior.
11. Cuando ya es conocido el valor de h se calcula d.ç
𝑆𝑒𝑛𝜃 =
ℎ
𝑑
𝑑=
ℎ
𝑆𝑒𝑛𝜃
= ℎ𝐶𝑜𝑠𝑐𝜃
Esto con el objeto de calcular las coordenadas totales de los puntos Q y R.
Se hace halando d porque es la distancia entre un nuevo punto y un punto
de coordenadas conocidas (2) sobre una dirección también conocida
(rumbo 2–3).
12. Con la distancia d y el rumbo 2 – 3 se descompone la recta 2 –Q en sus
coordenadas parciales las que sumadas a las coordenadas totales de 2
dará como resultado las totales del punto Q.
13. La distancia n se calcula teniendo en cuenta lo consignado en el paso 8: n
= m + h (Cotθ – Cotθ) para lo que todos los datos son conocidos.
14. EL rumbo de la recta Q – R está determinado por las condiciones del
problema y ya se calculó la distancia Q – R o sea n por lo que se puede
descomponer esta recta en sus coordenadas parciales, sumarlas a las
totales del punto Q y así obtener las de R.
15. Cuando se obtiene las coordenadas del punto R se completa la información
necesaria para calcular el área definitiva (1, 2, Q, R, 6, 7) por el método
matricial.
16. Se efectúa la comparación del área obtenida o calculada con la requerida,
la diferencia es el error de cálculo, el que al dividirse entre el área requerida
da el error unitario. El error unitario se compara con el error máximo
admisible que similar al dado en las particiones con un punto fijo.
17.