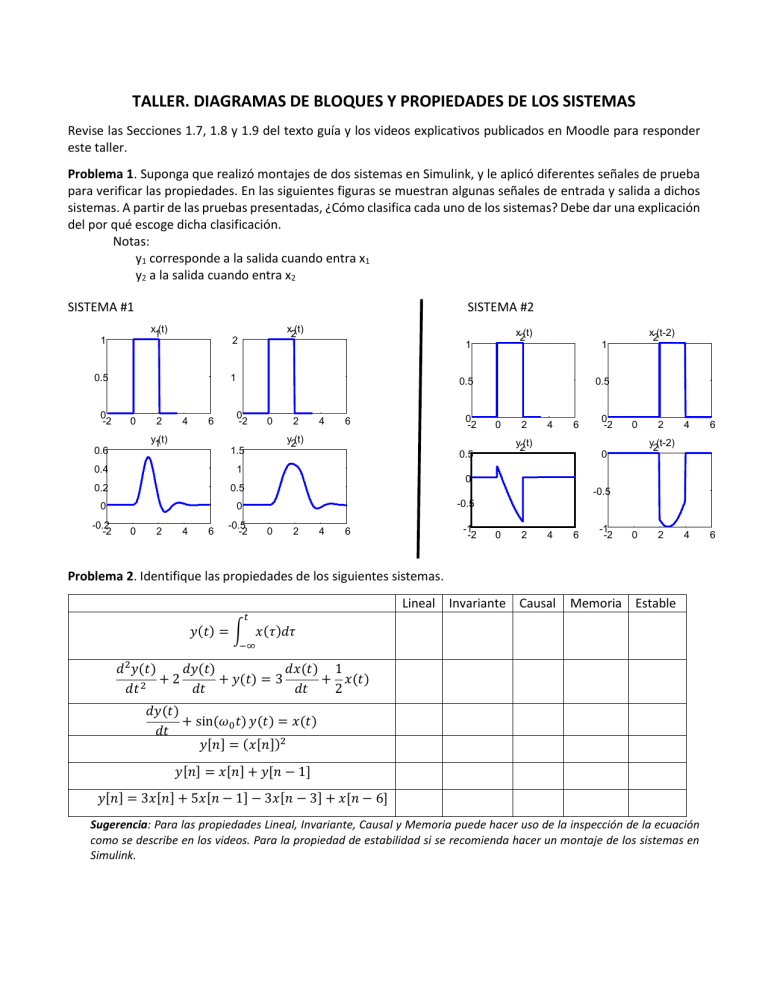
TALLER. DIAGRAMAS DE BLOQUES Y PROPIEDADES DE LOS SISTEMAS Revise las Secciones 1.7, 1.8 y 1.9 del texto guía y los videos explicativos publicados en Moodle para responder este taller. Problema 1. Suponga que realizó montajes de dos sistemas en Simulink, y le aplicó diferentes señales de prueba para verificar las propiedades. En las siguientes figuras se muestran algunas señales de entrada y salida a dichos sistemas. A partir de las pruebas presentadas, ¿Cómo clasifica cada uno de los sistemas? Debe dar una explicación del por qué escoge dicha clasificación. Notas: y1 corresponde a la salida cuando entra x1 y2 a la salida cuando entra x2 SISTEMA #1 SISTEMA #2 x1(t) 1 0.5 0 -2 x2(t) 2 1 0 2 4 6 y1(t) 0.6 0 -2 0.2 0.5 0 0 2 4 6 2 4 0 -2 6 0.5 0 y2(t) 1.5 1 0 0 x2(t-2) 1 0.5 0.4 -0.2 -2 x2(t) 1 2 4 6 y2(t) 0.5 0 -2 0 2 4 6 4 6 y2(t-2) 0 0 -0.5 -0.5 -0.5 -2 0 2 4 -1 -2 6 0 2 4 6 -1 -2 0 2 Problema 2. Identifique las propiedades de los siguientes sistemas. Lineal Invariante Causal Memoria Estable 𝑡 𝑦(𝑡) = ∫ 𝑥(𝜏)𝑑𝜏 −∞ 𝑑2 𝑦(𝑡) 𝑑𝑦(𝑡) 𝑑𝑥(𝑡) 1 +2 + 𝑦(𝑡) = 3 + 𝑥(𝑡) 2 𝑑𝑡 𝑑𝑡 𝑑𝑡 2 𝑑𝑦(𝑡) + sin(𝜔0 𝑡) 𝑦(𝑡) = 𝑥(𝑡) 𝑑𝑡 𝑦[𝑛] = (𝑥[𝑛])2 𝑦[𝑛] = 𝑥[𝑛] + 𝑦[𝑛 − 1] 𝑦[𝑛] = 3𝑥[𝑛] + 5𝑥[𝑛 − 1] − 3𝑥[𝑛 − 3] + 𝑥[𝑛 − 6] Sugerencia: Para las propiedades Lineal, Invariante, Causal y Memoria puede hacer uso de la inspección de la ecuación como se describe en los videos. Para la propiedad de estabilidad si se recomienda hacer un montaje de los sistemas en Simulink. Problema 3. Para los siguientes diagramas de bloque, encuentre la(s) ecuación(es) diferencial o en diferencias que representan dicho sistema. Problema 4. El reto del ecualizador Un estudiante curioso a quien le fascinaba la música, al leer sobre diagramas de bloques vio que los sistemas en tiempo discreto se pueden implementar sobre circuitos digitales, y quiso probar como usar este principio para montar un proyecto en Sistemas Digitales I. Como el estudiante era fanático de los ritmos musicales que incluyeran mucho bajo, estaba interesado en intensificar el sonido del bajo empleando un amplificador de mucha potencia y un parlante bien grande para esos tonos, dejando el resto de los sonidos para un parlante convencional. Investigando un poco encontró que muchos sistemas en tiempo discreto se llaman filtros digitales. Así que su proyecto consistió en montar un ecualizador digital que le permitiera separar los tonos bajos de los altos y así amplificar cada una de las señales usando diferentes amplificadores. El mancito encontró que en Matlab se puede calcular los coeficientes de un filtro digital basado en un filtro análogo Butterworth haciendo uso de la función butter de esta forma: [bk ak] = butter(N, Wn); donde ak y bk son los coeficientes de la ecuación en diferencias que acompañan las y y los x, respectivamente, 𝑎0 𝑦[𝑛] + 𝑎1 𝑦[𝑛 − 1] + 𝑎2 𝑦[𝑛 − 2] + ⋯ + 𝑎𝑃 𝑦[𝑛 − 𝑁] = 𝑏0 𝑥[𝑛] + 𝑏1 𝑥[𝑛 − 1] + 𝑏2 𝑥[𝑛 − 2]+. . . +𝑏𝑄 𝑥[𝑛 − 𝑁], N es el orden del filtro, y Wn es la frecuencia de corte del filtro pasa-bajo dividida por la mitad de la frecuencia de muestreo. Encontró en la documentación que esta función devuelve un filtro pasa-bajo, y si lo que se desea es un filtro pasaalto, pasa-banda o rechaza-banda se usa el formato [bk ak] = butter(N, Wn, tipo) donde tipo toma los valores 'highpass', 'bandpass', 'stop', respectivamente, y Wn, para el caso de pasa-banda o rechaza-banda, es un vector que contiene las dos frecuencias de corte del filtro dividas por la mitad de la frecuencia de muestreo. Para probar el sistema, al mancito le dio por hacerlo en Simulink, usando elementos de retardo, sumadores y ganancias que encontró en los componentes en la paleta Simulink→Discrete, y encontró que en los componentes de la paleta de Simulink DSP System Toolbox→Sources era posible importar un archivo .wav o .mp3 en Simulink y pasarlo por el diagrama de bloques del sistema en tiempo discreto. Igualmente, vio que en DSP System Toolbox→Sink, había forma de escribir en el parlante. ¿Será que usted es los suficientemente talentoso para hacer lo mismo del estudiante de la historia? ¿Será que usted puede montar la simulación en Simulink tal como lo hizo el mancito? ¿Será que usted puede hacer el diagrama de un circuito digital que implemente el sistema?