1. Gases Ideales + Reales

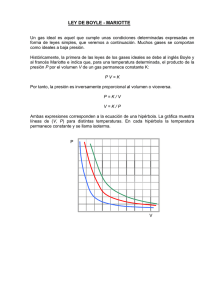
FISICOQUÍMICA
Dra. Guadalupe Canosa
FISICOQUÍMICA: Definición
PROBLEMÁTICAS
P/ QUÍMICOS
EXPERIENCIAS DE
LABORATORIO
Métodos
matemáticos
POSTULAR LEYES
FISICOQUÍMICA: Definición
La FISICOQUÍMICA es la ciencia en donde la física y la
matemática se aplican a la resolución de los problemas
fundamentales de la química
INGENIEROS
Usar estas leyes y conceptos para la resolución de
PROBLEMAS INDUSTRIALES
Sensibilidad
del V a P y T
Espacio
disponible
Superficies de
contorno
Gases
Líquidos
Sólidos
Alta
Casi nula
Llenan
completamente
Llenan
parcialmente
No llenan
No poseen
Límite a través de
una
Al menos una
Casi nula
LEY DE BOYLE Y MARIOTTE (1660-1670)
LEY DE BOYLE Y MARIOTTE
A temperatura constante, el volumen de una masa dada
de un gas es inversamente proporcional a su presión
P x V = cte
P1 x V1 = P2 x V2
LEY DE BOYLE Y MARIOTTE (Teoría cinética)
LEY DE BOYLE Y MARIOTTE (Teoría cinética)
T
LEY DE GAY-LUSSAC (1800)
LEY DE GAY-LUSSAC
A volumen constante, la temperatura absoluta de una masa
dada de un gas es directamente proporcional a su presión
P = cte x T
Por Boyle
V = cte x T
LEY DE GAY-LUSSAC
LEY DE GAY-LUSSAC
Otra forma expresa que el volumen de una masa dada de
cualquier gas aumenta en la misma cantidad relativa por
cada grado centígrado de aumento de la temperatura


Vt  V0   v *V0 * t
v  coeficiente de dilatación de los gases
t


Vt  V0 1   v * t  V0 1 

273
,
15


Si V1 y V2 son los volúmenes de una masa dada de un gas a las temperaturas t1 y t2

t1 

V1  V0 1 

273
,
15


V1
t  273,15
 1
V2 t2  273,15

t2 

V2  V0 1 

273
,
15


V1 V0 (1  t1 / 273,15)

V2 V0 (1  t2 / 273,15)
Si definimos una nueva escala de temperaturas Ti  ti  273,15
V1
T1

V2 T2
ECUACIÓN DE ESTADO DE LOS GASES IDEALES
Combinando los resultados de las leyes de Boyle y
Gay-Lussac
P1 V1  P2 V1'
A temperatura cons tan te
P1 V1
V 
P2
'
1
V1' V2

T1
T2
V1' 
A presión cons tan te
T1 V2
T2
P1 V1 P2 V2

T1
T2

PV
 cte
T
ECUACIÓN DE ESTADO DE LOS GASES IDEALES
El valor de la constante de los gases surge de considerar la
LEY DE AVOGADRO
R = 0,082 l atm/K mol
R = 2 cal/K mol
R = 8,31 J/K mol
LEY DE GRAHAM DE DIFUSIÓN
Estudió la difusión de diferentes gases a través de
medios porosos:
D1

D2
2
1
Como   PM
D1

D2
PM 2
PM1
Además D  1 / t
t2

t1
2

1
PM 2
PM1
LEY DE DALTON
La presión total de una mezcla de gases es igual a la suma de las
presiones parciales de los gases que componen la mezcla:
P  p1  p2  ...  pn
Otra forma puede obtenerse si suponemos que cada gas en
la mezcla se comporta como GI:
piV  ni RT
pV
n RT
PV  (n1  n2  ...  nn ) RT  nRT
pi
n
 i x
P
n
i
PV

i
nRT
pi  xi P
CÁLCULO DE CV (T. CINÉTICA)
Supongamos que tenemos un GI a volumen constante,
sus moléculas pueden:
TRASLADARSE
ROTAR
VIBRAR
CÁLCULO DE CV (COMPONENTE DE TRASLACIÓN)
Según el principio de equipartición cada forma de
energía manifestada por una molécula contribuye con
½ R la capacidad calorífica de un gas. Así, la capacidad
calorífica de cualquier molécula sería 3/2 R, por las
tres componentes de traslación:
Por definición de CV:
3
3
3
Cv traslación  R(T  1)  RT  R
2
2
2
CÁLCULO DE CV (COMPONENTE DE ROTACIÓN)
Esta se debe a la rotación de la molécula entera
alrededor de los tres ejes coordenados. Debido,
también, al principio de equipartición, la rotación
podría contribuir con un máximo de 3/2 R a la
capacidad calorífica del gas:
Cv rotación  0 *
Cv rotación  2 *
1
R0
2
1
RR
2
1
3
Cv rotación  3 * R  R
2
2
MOLÉCULAS MONOATÓMICAS
MOLÉCULAS DIATÓMICAS O POLIATÓMICAS
LINEALES
MOLÉCULAS POLIATÓMICAS NO LINEALES
CÁLCULO DE CV (COMPONENTE DE VIBRACIÓN)
La vibración aporta como máximo 2 x 1/2R a la
capacidad calorífica a volumen constante de un gas
por cada modo de vibración; esta se calcula usando la
siguiente expresión:
Cv vibración  3n  x R
n=número de átomos que forman la molécula
x=número de movimientos de rotación más traslación
CÁLCULO DE CV
Cv máximo  Cv traslación  Cv rotación  Cv vibración
3
3
Cv máximo  R  R  (3n  x) R
2
2
CÁLCULO DE CP
Al aumentar la temperatura pero en este caso
permitiendo que el gas se dilate, el sistema debe
hacer un trabajo extra al que realiza para aumentar la
Ecin para “vencer” la presión externa:
P
h
A
CÁLCULO DE CP
P
h
1
2
A
En el estado 1 el gas ejerce sobre el émbolo una
presión P=F/A. Para pasar al estado 2 debe realizar un
trabajo Wexp=F.d=P.(A.h)=P.ΔV
CÁLCULO DE CP
Wexp=P.ΔV
Para un mol de GI:
P.V=R.T
Si elevamos su temperatura 1K(a P cte): P(V+ΔV)=R(T+1)
Restando estas:
P(V+ΔV)-P.V=R(T+1)-R.T
P.V+P.ΔV-P.V=R.T+R-R.T
P.ΔV=R
Wexp=R
Cp  Cv  W exp  Cv  R
3
3
C p máximo  R  R  (3n  x) R  R
2
2
GASES REALES
Un gas real se comporta como ideal a:
PRESIÓN
TEMPERATURA
GASES REALES
Las leyes de los gases ideales pueden deducirse de la
teoría cinética de los gases y esta postula:
No hay fuerzas
El volumen de las moléculas es despreciable
Los choques son perfectamente elásticos
GASES REALES
Volumen de las moléculas del sólido?
Cómo pueden liguarse los gases?
ECUACIÓN DE VAN DER WAALS (GASES REALES)
Para la primera corrección considera que hay
fuerzas de atracción entre las moléculas y teniendo
en cuenta lo que le ocurre a una molécula cercana
a la pared del recipiente y a otra en el interior (y de
datos experimentales con gases reales):
Pideal  Preal
a
 2
V
ECUACIÓN DE VAN DER WAALS (GASES REALES)
Además como las moléculas tienen volumen, el
espacio que disponen para moverse es menor que
el real del recipiente:
Videal  Vreal  b
Donde b es denominado covolumen
ECUACIÓN DE VAN DER WAALS (GASES REALES)
a

P  2
V


 * V  b   R * T


a n2 
 P 
 * V  n b   n R * T
2 
V 
