1 El abuelo de Micaela quiere regalarle $ 100 cada semana

Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
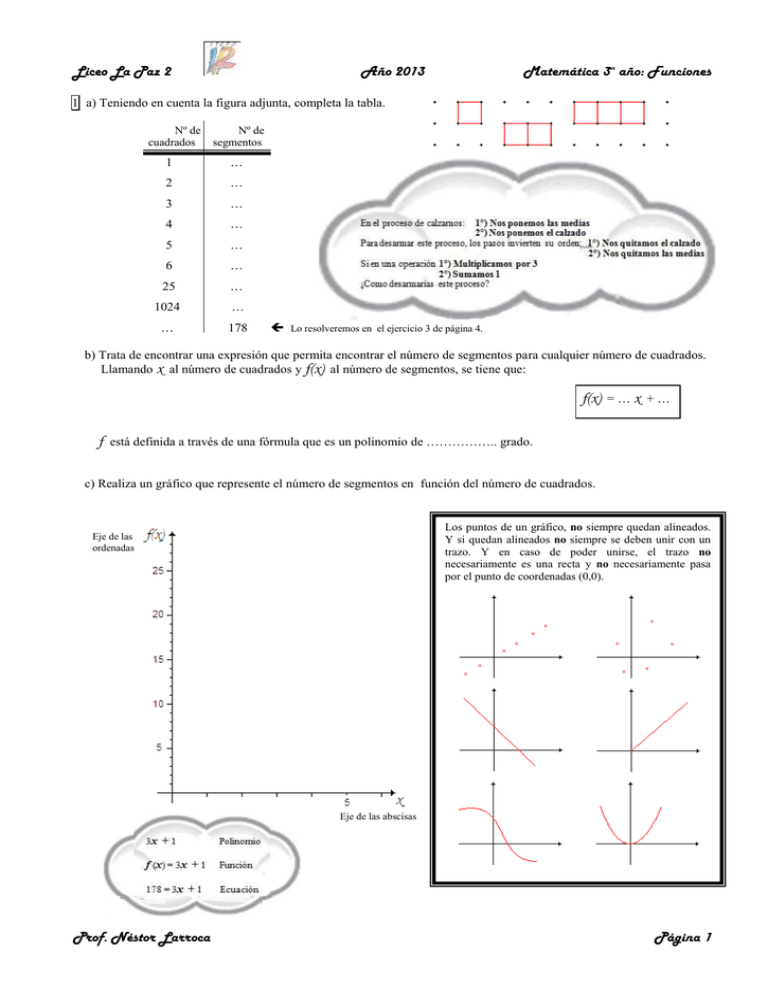
1 a) Teniendo en cuenta la figura adjunta, completa la tabla.
Nº de
cuadrados
Nº de
segmentos
1
…
2
…
3
…
4
…
5
…
6
…
25
…
1024
…
…
178
 Lo resolveremos en el ejercicio 3 de página 4.
b) Trata de encontrar una expresión que permita encontrar el número de segmentos para cualquier número de cuadrados.
Llamando x al número de cuadrados y f(x) al número de segmentos, se tiene que:
f(x) = … x + …
f está definida a través de una fórmula que es un polinomio de …………….. grado.
c) Realiza un gráfico que represente el número de segmentos en función del número de cuadrados.
Los puntos de un gráfico, no siempre quedan alineados.
Y si quedan alineados no siempre se deben unir con un
trazo. Y en caso de poder unirse, el trazo no
necesariamente es una recta y no necesariamente pasa
por el punto de coordenadas (0,0).
Eje de las
ordenadas
Eje de las abscisas
Prof. Néstor Larroca
Página 1
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
d) Un representante de computadoras recibe cada mes
US$ 500 fijos, más US$ 50 por cada equipo vendido.
A la izquierda tienes el gráfico que representa la
situación. La variable independiente (número de
aparatos vendidos) solo tiene sentido para los valores
0, 1, 2, 3, … y no para los “intermedios”, pues no se
puede vender un número fraccionario de
computadoras. La gráfica es discontinua porque la
variable independiente “se mueve a saltos”.
Nota
Cuando unimos los puntos de un gráfico estamos “afirmando” que además de los
puntos graficados, hay otros puntos, cuyas coordenadas son elementos de los
conjuntos con los cuales se trabaja.
En el grafico de la parte c) por ejemplo, si unimos los puntos A(1,4) y B(2,7)
estamos afirmando que la abscisa 1,4 del punto P pertenece al conjunto de salida, y
esto no es correcto, ya que “no hay” 1,4 cuadrados.
Otro ejemplo de un gráfico con discontinuidades
En otras ocasiones, aunque la variable independiente sea
continua, el gráfico presenta “saltos bruscos”. Estos saltos se
llaman discontinuidades. Un caso donde se presenta esta
situación, es por ejemplo, en el gráfico de una llamada
telefónica.
Consideremos cierta llamada telefónica cuyo costo es de $U 6
para comenzar, y con los cuales se puede hablar 3 minutos. A
partir de ese instante, cada minuto adicional cuesta $U 1. A la
derecha se muestra el gráfico respectivo.
Prof. Néstor Larroca
Página 2
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
2 Cuando en matemática queremos hacer referencia a un intervalo de números tenemos distintas maneras de expresarnos.
Por ejemplo para hacer referencia al intervalo de números entre 3 y 7 tenemos:
 observa que se ha pintado un intervalo de extremos 3 y 7
3 
x  7
[3,7]
 la x representa a los números del intervalo y la expresión nos dice que 3 es
menor o igual que los números del intervalo y que estos a su vez son menores
o iguales que 7.
 esta forma es también muy utilizada y se usan paréntesis rectos
También podrás encontrar en alguna tabla la siguiente manera 3–7 (pero seguro podrás deducir que esta forma no es
muy práctica ya que puede llevar a quien lo lea, a pensar en la operación sustracción y no en un intervalo).
Pero también nos puede interesar dejar fuera del intervalo, uno o ambos extremos del intervalo. Por ejemplo, si nos
interesara dejar fuera del intervalo, al número 7, tenemos:
 observa que se trazó oblicua la línea en el extremo 7
3 
x < 7
[3,7)
 observa que se cambio el signo de menor o igual después de la
signo de menor.
x por el
 observa que se cambió el paréntesis recto por uno curvo al final.
Esto nos agregaría un nuevo problema en la notación 3–7, pues ¿cómo darnos cuenta si se incluyen o no los extremos?
a) Las tarifas postales de una cierta empresa, están basadas en el peso para
paquetes pequeños como se muestra en la siguiente tabla:
¿Qué dificultades puedes encontrar en la interpretación de esta tabla?
b) ¿Puedes modificar la tabla para una mejor interpretación de la misma?
c) Julieta quiere enviar un paquete de 7g ¿cuál es la tarifa que le corresponde
pagar? ¿Y por 50,8g? ¿Y por 100g?
d) Paola quiere enviar a una amiga dos objetos de 48g y 190g respectivamente.
Decide si le será más barato enviar los dos objetos en un único paquete o
enviar los objetos en paquetes separados.
e) ¿Cuál de los siguientes gráficos es la mejor representación de las tarifas postales de esta empresa?
Prof. Néstor Larroca
Página 3
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
3 Otra forma de presentar los datos de un cuadro es mediante un diagrama de Venn. Estos diagramas se usan para
mostrar gráficamente la relación matemática o lógica entre diferentes conjuntos, representando cada conjunto mediante
un óvalo o círculo. Los diagramas de Venn reciben el nombre de su creador, John Venn, quien introdujo el sistema de
representación que hoy conocemos en julio de 1880. El método de Venn superaba en claridad y sencillez a los sistemas
de representación anteriores, hasta el punto de convertirse con el tiempo en un nuevo estándar.
Volvamos a los datos del ejercicio 1.
Nº de cuadrados
Nº de segmentos
“se trazan”
1
…
…
2
3
Conjunto de
…
4
salida
…
5
Conjunto de
llegada
…
6
…
Nota
Entre los diagramas de Venn, podemos poner la “expresión” que nos permite obtener, haciendo los cálculos
correspondientes, la imagen de los elementos del conjunto de salida.
“3x + 1”
1
4
Sustituimos la x por el valor correspondiente
2
7
Por ejemplo, para x = 1 tenemos:
3×1+1=3+1=4
Decimos que 4 es la imagen de 1, o que 4 es el correspondiente de 1 y que 1 es la pre imagen de 4.
Ecuaciones
Cuando en el ejercicio 1, tenemos que hallar el valor de x para que f(x) tome el valor 178, lo
que debes plantear es una ecuación:
3x + 1 = 178
Para resolver esta ecuación, habrás escuchado decir “pasamos el 1 restando” y escribir
entonces:
3x = 178 – 1
Debes tener presente que en realidad lo que has hecho es sumar a ambos miembros de la
igualdad un –1 (o lo que es lo mismo, has restado 1):
3x + 1 + (–1) = 178 + (–1)
3x + 1 – 1 = 178 – 1
Observa que en el primer miembro de la igualdad tienes +1–1 y esto resulta ser igual a 0 y
teniendo en cuenta que 3x + 0 = 3x de ahí resulta que 3x = 178 – 1 o lo que es lo mismo:
3x = 177
Para resolver esta ecuación habrás escuchado decir “pasamos el 3 dividiendo” y escribir
entonces:
x = 177
3
Debes tener presente que en realidad lo que has hecho es dividir ambos miembros de la
igualdad por 3, resultando:
3x
3 x 177
177
y como
= x tienes que x =
o sea x = 59.

3
3
3
3
Prof. Néstor Larroca
Página 4
Liceo La Paz 2
Año 2013
En resumen, el proceso de resolución de la ecuación anterior es el que sigue:
Matemática 3er año: Funciones
3x + 1 = 178
3x + 1 – 1 = 178 – 1
3x = 177
3 x 177

3
3
x = 59 
S = {59}
Nota:
a) Resuelve en forma análoga a la mostrada anteriormente las siguientes ecuaciones:
i) 5x + 9 = 44
ii) 2x + 1 = 6
iii) 6 x – 11 = 49
v) –3x + 8 = –4
vi) -4x + 20 = 0
vii) 1,5x + 7 = –6,5
iv) 4x – 7 = –21
viii) 1
x + 3 = –3
2
b) Deberías también poder resolver estas otras ecuaciones:
i) 9(x – 1)= 81
ii) 3(x + 5)= 21
iii) –15x – 75 = 16x – 292
iv) 4(x + 2) = 8x – 4
c) Material extraído del libro MATEMÁTICAS 3 de J. Colera y otros. Editorial ANAYA
Prof. Néstor Larroca
Página 5
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
4 Consideremos un cuadrado de lado 4 cm. De sus “esquinas” se cortan triángulos isósceles iguales, como se indica en la
figura. Llamemos “x” a la medida de los lados iguales en dichos triángulos.
x
x
Son triángulos rectángulos isósceles.
Catetos: son los lados que determinan el ángulo recto
Hipotenusa: es el lado opuesto al ángulo recto
a) ¿Cuándo diremos que el octógono resultante es regular?
b) Encuentra una expresión en función de “x” para hallar el área del octógono resultante.
El área del cuadrado es 
Á cuadrado =
El área de un triangulo es 
y el de los cuatro triángulos es 
Á triángulo =
Á 4 triángulos =
Á = ……. – ………...
c) ¿Qué valores puede tomar “x” para que exista el octógono”
….. < x < ….. o
o (0,2)
d) ¿Para que valores de “x” se tienen cuadrados?
Para
Prof. Néstor Larroca
x = …. y para x = ….
Página 6
Liceo La Paz 2
Año 2013
e) Completa la tabla adjunta.
Medida
“x” en cm
Matemática 3er año: Funciones
Área del
octógono en cm2
0,2
…
f (0,2) = –2 × 0,22 + 16
½
…
f () = –2 × ()2 + 16
¾
…
1
…
1,5
…
1,9
…
f) Llamando x a la medida del cateto del triángulo rectángulo isósceles y
f(x) = – 2….. + ….
f(x) al área del octógono, se tiene que:
donde …… es el término independiente
f está definida a través de una fórmula que es un polinomio de …………….. grado.
g) Realiza un gráfico que represente el área del
octógono en función de la medida x del cateto
del triángulo recortado.
Medida del cateto
Área del octógono
“….……………”
0,2

…
…

…
1
…
1,5
…
1,9
Prof. Néstor Larroca
h) Realiza diagramas de Venn para representar la relación anterior
…
Página 7
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Notas
I) ….. es la imagen de 1, por lo tanto el par ordenado (1 , ….) son las coordenadas de un punto P del gráfico.
Los elementos del par son (x , f(x)) o (x , y) o sea que escribimos como primera componente del par, el valor de
la abscisa del punto y como segunda componente, el valor de la ordenada del punto.
x
f(x)
II) El gráfico anterior es parte de una curva que recibe el nombre de “parábola”
Ubica en el gráfico los puntos M y M’ de ordenada 8
Completa:
M(….,8)
M’(….,8)
Sabemos que en los puntos A y B la ordenada es …….
Para hallar la abscisa de dichos puntos sabemos entonces
que:
-2x2 + 16 = 0
Esta es una ecuación de segundo grado (la incógnita está elevada al exponente 2)
-2x2 + 16 – 16 = 0 – 16 (sumamos -16 a ambos miembros de la igualdad)
-2x2 = ….
 2 x 2  16

2
2
(dividimos entre -2 ambos miembros de la igualdad)
x2 = ….
(buscamos un número que elevado al cuadrado no de 8)
x   8 y hallando una expresión decimal aproximada tenemos que x =  ……….
Entonces el conjunto solución es
S={
8 ,
8}
III) En este caso los puntos del gráfico si, se pueden unir, pues para todo valor de x comprendido entre …. y ….
tenemos un valor correspondiente de área del octógono.
Repasando brevemente la operación Radicación
índice (si es 2 no lo escribiremos)
Si tenemos
radical
2
9 3
raíz (en este caso raíz cuadrada)
radicando
SE DEFINE
Prof. Néstor Larroca
Página 8
Liceo La Paz 2
Año 2013
Como debe ser b ≥ 0, por ejemplo es
Matemática 3er año: Funciones
49 = 7 y no consideramos la solución –7, pues si bien (–7)2 = 49 la notación
49 esta reservada para la raíz cuadrada positiva de 49.
Si deseamos la raíz cuadrada negativa debemos escribir –
La ecuación x2 = 64 tiene dos soluciones (x = 8

x2 = 64
49 = – 7.
x = – 8) por lo que para considerar ambas soluciones plantemos
y

x =  64

x=±8
S = {–8,8}
Las raíces cuadradas de números negativos no están definidas en el conjunto de los números reales (ya hablaremos de
 4 no está definida ya que no existe ningún número real que elevado al
ellos más adelante en el curso). Por ejemplo
cuadrado de – 4.
 4  R pues  x  R  x2 = – 4
 no pertenece  no existe  tal que
Recordar que se define valor absoluto de un número como el módulo del número, o sea como la distancia desde el número
hasta cero, en la recta de los números reales. Y como la distancia es siempre positiva o cero, el valor absoluto de un número
es siempre mayor o igual a cero.
-4
Las barras se leen “Valor absoluto de”
-3

-2

-1
0
1
2
3
4
3=3
5 5

2 2
a
si a ≥ 0
Si a es un número real, entonces el valor absoluto de a es  a  =
–a si a < 0
 5
 2
Obsérvese que     
5
2
Lo leeremos como opuesto de a.
Tener presente que -a no significa que sea un número negativo pues:
42  16 = 4 =  4  pues  4  = 4
Nota
(en este caso a = 4)
( 4) 2  16 = 4 = – 4  pues – 4  = 4
Así que
si a = 5
 – a = –5
si a = – 4  – a = – (–4) = 4
(en este caso a = – 4)
a 2  a solo si a ≥ 0, pues si a < 0 no es cierto que a 2  a como se muestra anteriormente.
Sin embargo siempre podremos escribir
a2  a
52  5  5
(7) 2   7  7
Resuelve
a)
81  ….
b)
 121  ….
c)
f)
(8) 2  .....  ...
g)
20  ….
d)
 12  ….
Completa
e)
112  ....  ....
Prof. Néstor Larroca
 6 2   … = ….. h)  0,25  ….
Página 9
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
5 Resuelve las siguientes ecuaciones de segundo grado:
a) 3x2 – 27 = 0
2
b) 3x2 – 70 = 5
c) (x + 5)(x – 5) = 0
2
2
f) 1,6x2 = 0,144
d) -7x + 35 = 0
e) -2x + 256 = 2x
g) 4x2 + 20 = 0
h) (x – 12)(x + 12) = 0
i) –x2 + 16 = 0
Propiedad Hankeliana o ausencia de divisores de cero.
“Si a y b son números reales y a por b es igual a cero,
entonces a es igual a cero y/o b es igual a cero”
En algunos casos, la propiedad Hankeliana, será la única forma en la cual puedan apoyarse “por ahora” para hallar las
raíces de una ecuación.
Por ejemplo si tenemos las ecuaciones:
i) (2x + 4)(2x – 10) = 0
ii) (x 2 – 49)(x – 6) = 0
y aplicamos propiedad distributiva desarrollando para intentar hallar las raíces , tendremos ecuaciones de segundo (caso
i) y tercer grado (caso ii) que no podrán resolver con los conocimientos actuales.
Se tendrán:
i) 4x 2 – 12x – 40 = 0
→ ecuación de 2do grado completa
ii) x 3 – 6x2 – 49 x + 294 = 0 → ecuación de 3er grado completa
Sin embargo aplicando la propiedad Hankeliana estas ecuaciones son fácilmente resolubles:
 x=–2
2x + 4 = 0
(2x + 4)(2x – 10) = 0 

o
S = {–2,5}
2x – 10 = 0  x = 5
Ejercicio:
Resuelve la ecuación del caso ii) y las siguientes
iii) (–3x + 9)(4x – 7) = 0
iv) (–2x 2 + 2)(4x – 10) = 0
6 Consideremos parte del plano de una ciudad y algunos edificios en él.
Representemos el conjunto A de edificios y el conjunto B de calles.
Relacionemos los elementos de ambos conjuntos mediante la relación “está
sobre la calle”. Traza tu las “flechas” correspondientes.
A
B
“está sobre la calle”
a
2
4
b
3
c
d
5
6
a) ¿Cuál es el tipo de edificios más comunes en una ciudad?
e
1
b) Si coloco un nuevo edificio, ¿cuántos correspondientes podrá tener?
Observa que hay elementos sin correspondiente (el …..) y otros con más de un correspondiente (el ….. , …... y ……)
c) ¿Qué diferencia importante tiene el diagrama de Venn de este ejercicio, con los diagramas de Venn de los dos
ejercicios anteriores? Los ejercicios anteriores son el 3 de la página 4 y el 4 de la página 6.
Prof. Néstor Larroca
Página 10
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
A las relaciones entre conjuntos, que tienen las características de los ejercicios anteriores le llamaremos funciones. La
palabra función fue introducida en el lenguaje matemático por Gottfried Wilhelm von Leibniz.
DEFINICIÓN
En una función llamaremos dominio al conjunto de partida (tener presente que para que una relación sea función todos los
elementos del conjunto de partida tienen correspondiente) y codominio al conjunto de llegada. Los elementos del
codominio que son imagen de algún elemento del dominio, determinan un conjunto que se llama recorrido de la función
Una función puede ser presentada de distintas maneras.
1) Mediante diagramas de Venn.
Los dos diagramas siguientes
corresponden a funciones.
 Indica porqué estos diagramas no corresponden a funciones
Piensa en una sala de cine, diagrama cada una de las situaciones que se te indican y comenta si los diagramas obtenidos
corresponden a funciones
a) Hay más espectadores que butacas, por lo tanto hay espectadores de pie.
b) Cada espectador ocupa una butaca, no hay butacas vacías ni espectadores
de pie.
c) Hay espectadores que concurrieron con hijos pequeños y la sala tenía
todas las butacas vendidas a adultos.
d) Hay menos espectadores que butacas y todos están sentados.
e) ¿Puede darse una situación como la relación establecida entre los
conjuntos G y H anteriores?
2) Mediante un gráfico.
Los dos gráficos siguientes son ejemplos de
gráficos de funciones.
 Indica porqué estos gráficos no corresponden a funciones
Tarea: Representa tu algún gráfico que corresponda al de una función y otro que no corresponda.
Prof. Néstor Larroca
Página 11
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Nota: Para que un gráfico corresponda al de una función, toda recta paralela al eje de las ordenadas, por un valor de
abscisa correspondiente al dominio de la relación, debe intersecar en un solo punto al gráfico.
3) Mediante una expresión algebraica.
f (x) = 2x + 8
donde
f es el nombre de la función
(x) indica la variable utilizada en la expresión
2x + 8 es la expresión que determina la función
g (x) = – x + 1
2
¿Cuál es el grado de la función f ? ¿Y el de la función g ? ¿Y el de la función h siendo h (x) = 8x2 + 2x + 1 ?
4) También una función puede presentarse por un conjunto de pares o por una tabla como la que sigue
F = {(1,4) , (2,7) , (3,10) , (4,13) , (5,16)}
El par (1,4) nos indica que 4 es la imagen de 1.
Observa que estos pares corresponden a la función de expresión f (x) = 3x + 1
¿Te animas a determinar la expresión de la función en los siguientes conjuntos de pares?
G = {(–2,–6) , (0,–2) , (1,0) , (2,2) , (5,8)}
 g (x) = …x – ….
H = {(–1,4) , (0,3) , (1,4) , (2,7) , (3,12) , (5,28)}
 h (x) = ….. + ….
7 Todos los números naturales y todos los números enteros se pueden representar con expresiones decimales periódicas,
de período cero.
Así tenemos:
4 = 4,0000000…
o sea
– 5 = – 5,000000…
o sea
Tanto los números naturales como los enteros, además de poder representarse con expresiones decimales periódicas,
también pueden ser representados con fracciones.
Así tenemos 4 
4
1
o 5 
5
1
Son números racionales todos aquellos números que pueden ser representados por fracciones, así son racionales los
naturales y los enteros y otros como por ejemplo 
El conjunto de los naturales se representa con una
, -  , -  , .
, el de los enteros con una
y el de los racionales con una
.
Los números racionales pueden tener expresiones decimales exactas o periódicas. Así tenemos
3
 0,75
4
1
 0,3
3
Los racionales con expresiones decimales exactas, al igual que lo hicimos con los naturales y los enteros los podemos
3
 0,75  0 , 7 5 0
4
18
9
 1, 8 0 o
 1,1 2 5 0
10
8
representar con expresiones periódicas de período cero. Por lo tanto es
Otros ejemplos son:
7
 0,583
12
o
41
 3, 7 2
11
o
Por lo tanto diagramemos un conjunto al que llamaremos de los números reales, que representaremos con una
estará formado por números con expresiones decimales periódicas, llamados números racionales
con expresiones decimales con infinitas cifres decimales no periódicas, llamados números irracionales
Prof. Néstor Larroca
y que
y por números
.
Página 12
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
4
 4,0
 Números racionales
1
5
5 
 5 , 0
1
4
Números irracionales 
9
 1,1 2 5 0
8
41
 3, 7 2
11
Ahora, ¿existirán números que no tengan expresiones decimales periódicas?
Respuesta: Si
Tener presente, que estos números no serán racionales, y por lo tanto no hay fracción alguna que los represente. Dos de
ellos los conoces con seguridad:
 = 3,1415926535897932384626433832795...
Visita la página http://mimosa.pntic.mec.es/jgomez53/matema/conocer/numpi.htm
2  1,4142135623730950488016887242097…
¿Te animas tu a inventar dos o tres expresiones decimales, no periódicas?
Consideremos ahora, la representación de estos números en la recta numérica.
Entre 2 y 3 tenemos infinitos racionales.
Por ejemplo tenemos
7
 2,3
3
11
 2,75 .
4
y
Entre estos dos racionales (entre 2 y 3) existen infinitos otros, decimos que los racionales son densos. Para hallarlos
podemos encontrar fracciones equivalentes a estas, con el mismo denominador.
En este caso consideremos a
2
2
1
y a 3
210 20 200 200.000.000.000



110 10 100 100.000.000.000
3
1
310 30 300 300.000.000.000



110 10 100 100.000.000.000
y
Seguro que tu podrías indicar cuantos racionales quieras comprendidos entre 2 y 3.
Y si quisiéramos encontrar racionales entre
7
3
y
11
trabajaríamos en forma análoga, primero reduciendo las
4
fracciones que los representan, a común denominador.
74 28 280 280.000.000.000



34 12 120 120.000.000.000
Entonces tenemos que
7 29 11


3 12
4
o
y
7 291 11


3 120 4
113 33 330 330.000.000.000



43 12 120 120.000.000.000
o
7 290 .000 .000 .001 11


3 120 .000 .000 .000 4
Cuánto mayores sean los números que utilicemos para escribir las fracciones equivalentes, más fácil nos “damos cuenta”
que existen infinitos racionales entre los dos dados.
Prof. Néstor Larroca
Página 13
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Pero aunque pase esto, si miramos con una lupa veremos algo así
SI !!! aunque no lo creas, entre los racionales hay “huecos”. ¿Quienes ocupan esos lugares?
Respuesta: Los irracionales
Por lo tanto para asegurarnos que todo punto tiene su abscisa correspondiente debemos trabajar con racionales
irracionales
, o sea con los números reales
e
.
De aquí en más nuestro trabajo con funciones numéricas se hará trabajando tanto en el conjunto de partida, como en el
de llegada con números reales. De esta forma, nos aseguramos que todo punto tiene su abscisa y ordenada
correspondiente, lo que nos permitirá, unir los puntos de un gráfico.
Así tenemos, que todo punto entre P y Q tendrá su abscisa “a” y su
ordenada “b” correspondiente.
Por ello, cuando trabajemos con funciones numéricas, es importante “especificar” con que conjuntos trabajaremos en el
dominio y codominio, lo que se hace de la siguiente manera:
f:RR
/ f (x) = 2x + 8
dominio
codominio
f:RR
/ f (x) = – x2 + 1
Nota
En el ejercicio 1, nuestra función f era f : N  N
/ f (x) = 3x + 1
Recordemos el teorema de Pitágoras
En todo triángulo rectángulo, el cuadrado de la medida
de la hipotenusa es igual a la suma de los cuadrados de
las medidas de los catetos.
a2 = b2 + c2
En un cuadrado de lado 1, calculemos la medida de su hipotenusa
x2 = 1 2 + 1 2
x2 = 2
x=  2
En este caso, la solución “válida” es x = 2 ya que la distancia entre los puntos P y Q debe ser positiva. Por lo tanto
tenemos un segmento, cuya medida es un número irracional.
Para ubicar el punto que tiene dicha abscisa en la recta numérica,
podemos ayudarnos con el uso de un compás.
Ejercicios: (extraídos del libro Matemática 3 de C. Ochoviet y M. Olave de Editorial Santillana)
a) Encuentra una regla que pudo usarse para generar los siguientes números. Indica si son racionales o irracionales y
escribe sus seis cifras decimales siguientes:
5,78907890……………..
-8,212223……………………
89,551551………………………
89,551552………………
-11,220157999………………
3,232232223……………………
Prof. Néstor Larroca
Página 14
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
b) Trabajaremos con las siguientes rectas numéricas. En la primera representaremos solamente números naturales, en la
segunda, solamente números enteros, en la tercera solo números racionales y en la cuarta, reales.
 Representa los siguientes números en la o las rectas que correspondan:

1
7
3
; 3 ;  ; -2 ; ;  ;
2
2
4
3;
5
; 4 ; -4 ;  3
4
 Imagina que en la primer recta se han representado a todos los números naturales, ¿se cumple que a todo número
natural le corresponde un punto de la recta y a cada punto de la recta le corresponde un número natural?
 Analiza la pregunta anterior para los casos de las otras tres rectas
c) Se te muestra a continuación, como es posible simplificar la escritura de algunas expresiones:
Responde ahora con V o F a las siguientes afirmaciones:
8 Una función, determinada por una expresión como la que sigue:
f:RR
/ f (x) = 2x + 8
es una función de primer grado, ya que el exponente de la variable x es 1. En alguna bibliografía la encontrarás con el
nombre de función afín.
Visita http://thales.cica.es/rd/Recursos/rd98/Matematicas/05/definicion.html
Prof. Néstor Larroca
Página 15
Liceo La Paz 2
Año 2013
Genéricamente escribimos  f : R  R
Matemática 3er año: Funciones
/ f (x) = mx + n
Piensa
En f (x) = 2x + 8 es m = ……
y n = ……
h (x) = x – 3 es m = ……
y n = ……
La función afín es aquélla que asocia a cada número x el número mx + n, donde m y n son dos valores fijos,
m se llama pendiente y n ordenada en el origen.
Las funciones afines se representan mediante rectas. En consecuencia sólo se precisan solo un par de puntos para
obtener su gráfico.
f:RR
Por ejemplo, si tenemos
/ f (x) = 2x + 8.
Para hallar la raíz:
2x + 8 = 0
2x = – 8
x=–4
 Decimos que x = – 4 es la raíz de f  El punto (– 4 , 0) pertenece al gráfico de f .
Observa, además que si calculamos f (0) tenemos que
f (0) = 2.0 + 8
f (0) = 8
 El punto (0,8) 
G( f ).
Se tiene que
Con los dos puntos que tenemos, ya podemos determinar el gráfico de la
función f.
Cuando el coeficiente “m” de x en la función afín es positivo, decimos
que la pendiente es positiva.
La recta que representa al gráfico de la función, tiene ecuación:
y = 2x + 8
El gráfico de la función “interseca” al eje de las abscisas en el
valor de la raíz y al eje de las ordenadas en el valor de la
ordenada en el origen.
Por ejemplo, si tenemos
g:RR
/ g (x) = –3x + 6.
Para hallar la raíz:
–3x + 6 = 0
–3x = – 6
x = 2  Decimos que x = 2 es la raíz de g
Observa, además que si calculamos g (0) tenemos que
g (0) = – 3.0 + 6
g (0) = 6
Prof. Néstor Larroca
 El punto (2 , 0) pertenece al gráfico de g .
 El punto (0,6) 
G( g ).
Página 16
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Con los dos puntos que tenemos, ya podemos determinar el gráfico de la
función g.
Cuando el coeficiente “m” de x en la función afín es negativo, decimos
que la pendiente es negativa.
La recta que representa al gráfico de la función, tiene ecuación:
y = –3x + 6
El gráfico de la función “corta” al eje de las abscisas en el valor de la raíz
y al eje de las ordenadas en el valor de la ordenada en el origen.
i) f : R  R
/ f (x) = –3x + 9
ii) g : R  R
/ g (x) = 2x – 2
iii) h : R  R
/ h (x) = –x + 7
iv) t : R  R
/ t (x) = 5x + 10
9 a) Dadas las siguientes funciones de primer grado halla raíz y grafica
b) Realiza el gráfico de las funciones
i) k : R  R
/ k (x) = –4x
ii) d : R  R
/ d (x) = 5x
Este tipo de funciones en las cuales la ordenada en el origen es ….. reciben el nombre de función lineal.
Visita http://descartes.cnice.mec.es/materiales_didacticos/Funcion_lineal/Funcion_lineal.htm
10 Vamos a ver cómo podemos hacer rápidamente una tabla de valores de una función matemática trabajando con Open
Office Calc. Por ejemplo vamos a hacer una tabla de la función f (x) = 2x + 4 en el intervalo [-4,2], es decir vamos a
permitir que la x tome valores comprendidos entre –4 y 2.
f : [-4,2]  R
/ f (x) = 2x + 4
Por ejemplo:
si x = 1 tenemos que f (1) = 2  1 + 4 o sea que f (x) = 6
si x = –3 tenemos que f (-3) = 2  (–3) + 4 o sea que f (x) = –2
En primer lugar hay que decidir cuántos valore necesitamos. Desde –4 hasta 2 van 6 unidades.
Vamos a dividir cada unidad en 2 partes
Teniendo en cuenta que calcularemos el valor inicial y el valor final necesitamos un total de 13 puntos, es decir vamos a
utilizar el rango A1:B14 pues incluiremos títulos para las columnas. Para introducir los valores de x debes proceder de
la siguiente manera:
Prof. Néstor Larroca
Página 17
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
 Introduce en las celdas A1 y B1 los encabezados de las columnas.
 Introduce en la celda A2 el primer valor del intervalo. En nuestro caso -4.
 Introduce en la celda A3 la fórmula que permite calcular el siguiente valore de x. Si hemos dicho que dividimos cada
unidad en 2 partes, el siguiente valor de x se obtiene sumando 0,5 al anterior. Por lo tanto, la fórmula que debemos
escribir en A3 es =A2+0,5
 Copia la fórmula anterior y pégala en el rango A4:A14.
 Introduce ahora en la celda B2 la fórmula que representa a la función que estamos analizando.
Nuestra función consiste en multiplicar por 2 el valor que aparece en la celda de al lado y
luego sumar 4. Así pues, la fórmula que debes escribir en B2 es =A2*2+4
 Copia esa fórmula y pégala en el rango B3:B14.
 Define borde inferior de 2.50 pt para las celdas A1 y B1 y borde derecho de 2.50 pt para el rango A1:A14 y
establece centrado para ambas columnas.
Pasemos ahora a realizar el gráfico de dicha función. Para ello selecciona primero el rango A1:B14 y luego el icono
de la Barra de Herramientas Estándar.
Para el gráfico ten presente que:
 el Tipo de gráfico es XY (dispersión) tipo Puntos y líneas.
 el Rango de datos es $Hoja1.$A$1:$B$14 y marca las casillas correspondientes a Serie de datos en columna y
Primera fila como etiqueta.
 en Series de datos, debes tener lo que se muestra.
 Edita el gráfico y modifica colores de ejes, tamaño de los puntos, color
del gráfico, escalas de los ejes, etc., para que quede similar a como se
muestra.
Si en la hoja del ejercicio anterior cambias el valor –4 de la celda A1 por
-1, obtendrás una nueva tabla de la función en otro intervalo. ¿Cuál es el
nuevo intervalo?
Prof. Néstor Larroca
Página 18
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
11 Siguiendo el esquema de trabajo del ejercicio anterior haz una tabla de valores con 25 puntos de las siguientes funciones
en los intervalos que se indican:
 f : [-2,4]  R
/ f (x) = x – 1
 f : [-3,3]  R
/ f (x) = –2x + 2
 f : [2,8]  R
/ f (x) = x – 5
 f : [-5,1]  R
/ f (x) = –2x – 4
 f : [-4,2]  R
/ f (x) = 3x + 6
12 Vamos a representar ahora la función:
f : [-2,2]  R
/ f (x) = x2
Para ello haz una tabla de valores de la función en el intervalo [-2,2]. Desde –2 hasta 2 van 4 unidades, y vamos a dividir
cada unidad en 10 partes. Teniendo en cuenta que calcularemos el valor inicial y el valor final necesitamos un total de
41 puntos, es decir vamos a utilizar el rango A1:B42 incluyendo títulos para las columnas.
Por ejemplo:
si x = 1 tenemos que f (1) = 12 o sea que f (x) = ….
si x = –0,5 tenemos que f (-0,5) = (–0,5)2 o sea que f (x) = ……
Para introducir los valores de x debes proceder de la siguiente manera:
 Introduce en las celdas A1 y B1 los encabezados de las columnas.
 Introduce en la celda A2 el primer valor del intervalo. En nuestro caso –2.
 Introduce en la celda A3 la fórmula que permite calcular el siguiente valore de x. Si hemos dicho que dividimos cada
unidad en 10 partes, el siguiente valor de x se obtiene sumando ….. al anterior. Por lo tanto, la fórmula que debemos
escribir en A3 es =A2+…..
 Copia la fórmula anterior y pégala en el rango A4:A42
 Introduce ahora en la celda B2 la fórmula que representa a la función que estamos analizando. Nuestra función
consiste en elevar al cuadrado el valor que aparece en la celda de al lado. Así pues, la fórmula que debes escribir en
B2 es =A2^2
 Copia esa fórmula y pégala en el rango B3:B42.
 Realiza el gráfico de dicha función. Edita el gráfico y modifica colores de ejes, tamaño de los puntos, color del
gráfico, escalas de los ejes, etc.
13 Siguiendo el esquema de trabajo del ejercicio anterior haz una tabla de valores con 41 puntos de las siguientes
funciones en los intervalos que se indican:
 f : [-1,3]  R
/ f (x) = x2 + 1
 f : [-2,2]  R
/ f (x) = –2x2 – 2
 f : [2,6]  R
/ f (x) = –x2 – 8x + 15
 f : [-3,1]  R
/ f (x) = –3x2 – 6x
14 Otro programa que podemos utilizar para representar nuestros gráficos es el Geogebra.
En el ejercicio 10 representamos la function
f : [-4,2]  R
/ f (x) = 2x + 4
Si en la línea de entrada de texto, que se halla en la parte inferior de la ventana, digitamos 2x + 4
Prof. Néstor Larroca
Página 19
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Al presionar la tecla Enter, observaremos que inmediatamente se grafica nuestra función.
En la parte izquierda de la ventana de Geogebra
tenemos lo que se denomina la Vista Algebraica, que
puedes cerrar con el botón

correspondiente.
Observa que en la carpeta de objetos libres ahora
tenemos la función:
f (x) = 2x + 4
Por defecto el Geogebra trabaja con f : R  R
A las distintas vistas puedes acceder desde la barra de menús, en la opción Vista
Prof. Néstor Larroca
Página 20
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
También en Geogebra podemos construir una tabla de valores tal cual lo hemos hecho en la planilla de cálculo. Para
ello debes seleccionar desde la opción Vista – Vista de Hoja de Cálculo.
La ventana de Geogebra se dividirá en tres partes y a la derecha aparecerá la planilla de cálculo.
Haremos lo mismo que en Calc. En A1 ingresaremos el valor -4 y en A2 la fórmula:
= A1 + 0.5
Debes usar el punto como separador decimal y luego copias la fórmula hasta la celda A13.
En la celda B1 ingresas la fórmula:
= 2 * A1 + 4 y copias la fórmula hasta B13
Luego seleccionas el rango A1:B13 y con botón derecho haces clic en alguna celda del rango seleccionado.
Aparecerá un menú contextual del cual debes elegir la opción Crear Lista de Puntos.
Prof. Néstor Larroca
Página 21
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Observarás que en la Vista Grafica aparecen los puntos que tienen por coordenadas los valores de la tabla construida.
Puedes seleccionar en la opción Vista – Cuadricula para observar un cuadriculado en el gráfico.
Observa que en la Vista Algebraica, aparece en la carpeta de Objetos Dependientes, una lista de puntos (es un conjunto
de pares ordenados que correspondes a las coordenadas de los puntos del gráfico).
Puedes por último seleccionar la herramienta Recta que pasa por Dos Puntos y haciendo clic por ejemplo en P 1 y P13
observarás que los 13 puntos están alineados.
Otra forma de lograr unir los puntos es si en la línea de Entrada pones:
ajustepolinómico[lista1,1]
Entre paréntesis recto va como primer argumento lista 1, pues es el nombre de la lista de puntos a graficar y como
segundo argumento luego de la coma un 1 pues el polinomio que determina la función es de grado 1.
Prof. Néstor Larroca
Página 22
Liceo La Paz 2
Para graficar la función  f : R  R
Año 2013
Matemática 3er año: Funciones
/ f (x) = x2 + 1 puedes ingresar en la línea de entrada la expresión
O construir una tabla donde en A1 ingreses por ejemplo -3 y en A2 la fórmula = A1 + 0.5
En B1 ingresas =A1*A1+1. Recuerda que debes pintar el rango para Crear la Lista de Puntos.
Por último en la línea de entrada digitas:
ajustepolinómico[lista1,2] (2 porque el polinomio es de 2do grado)
Resultará algo así:
Si quieres cambiar la escala de los ejes, puedes seleccionar el botón Desplazar Vista Gráfica de la Barra de
Herramientas y al hacer clic sobre alguno de los ejes (verás que el cursor del ratón se transforma en una mano) sin
soltar el botón del ratón mueves y cambias la escala.
Prof. Néstor Larroca
Página 23
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
15 En algunos casos como en f : R  R / f (x) = 3x – 30, resulta un poco incómodo realizar el gráfico de la función pues
el valor de la ordenada en el origen es un número “grande”.
Por eso te será conveniente, atender el siguiente procedimiento que te será útil en Física, donde también trabajarás el
concepto de pendiente.
La pendiente nos permite obtener el grado de inclinación que tiene una recta.
Si los coeficientes de x son positivos y m > m’ siendo la ordenada en el origen la
misma, tenemos un gráfico como el que se muestra.
Si m = 5 ¿cuál podría ser el valor de m’ ?
¿Cuál podría ser el valor de n ?
Dada una recta, gráficamente su pendiente nos da su grado de inclinación.
Pendiente positiva
Cuando la recta es creciente (al
aumentar los valores de x aumentan
los de y), su pendiente es positiva, en
la expresión analítica m > 0
Ejemplo: y = ….x + ….
Pendiente negativa
Cuando la recta es decreciente (al
aumentar los valores de x disminuyen
los de y), su pendiente es negativa, en
la expresión analítica m < 0
Ejemplo: y = ….x + ….
y = ….x – ….
Pendiente nula
Cuando la recta es
constante se dice que tiene
pendiente nula, en la
expresión analítica m = 0
Ejemplo: y = ….x + ….
y = ….x
y = ….
En Física definirás pendiente como el cociente
entre y y
 y = y2
x (al símbolo  lo lees: “delta”).
– y1
 m
 x = x2
y 2  y1
x 2  x1
– x1
Si en ambos ejes trabajamos con la misma escala, la pendiente de una
recta coincide con la tangente trigonométrica del ángulo indicado (más
adelante en el curso nosotros trabajaremos Trigonometría).
Si trabajamos con distintas escalas en los ejes, la pendiente se seguirá determinando
como y / x pero no la podremos igualar a la tangente.
tg
Prof. Néstor Larroca

=
3
entonces la pendiente es m = 3.
1
Página 24
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
3x – 30 = 0
3x = 30
x = 10
Por lo tanto cuando se nos pide que grafiquemos la
función f : R  R / f (x) = 3x – 30, podemos
hallar la raíz y luego determinar un triángulo, con
un vértice en el punto que tiene el valor de la
abscisa que coincide con la raíz, de tal forma que el
cociente de las medidas de los catetos sea 3. Para
ello es conveniente que sea x = 1 y y coincida
con el valor de la pendiente.
Si tenemos la función g : R  R
Ubicada la raíz sobre el eje
de las abscisas, contar una
unidad siempre “hacia” la
derecha primero.
/ g (x) = –2x – 16
Es la raíz
También puedes realizar esto en Geogebra.
La ecuación de la recta la escribe 2x + y = –16
Observa cómo pueden quedar los triángulos sombreados y cómo no!!!
d) i) Realiza un bosquejo de las rectas de ecuación
r) y = –5x + 3
s) y = 7x – 5
ii) Escribe una posible ecuación para las rectas representadas.
Prof. Néstor Larroca
Página 25
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
e) Traza el grafico de cada función ejercitando lo anterior:
f:RR
/
g:RR /
h:RR /
t:RR /
f) Halla la pendiente de la rectas que pasan por los puntos:
f (x) = 6x + 24
g (x) = 2x – 7
h (x) = –5x – 16
t (x) = – x + 18
i) A(2,6) y B(3,10)
 determina la ecuación
ii) P(–1,2) y Q(–2,–1)
iii) H(3,–5) y T(5,-7)
g) ¿Cuál es la ecuación de la recta que:
i) pasa por P(4,–6) y tiene pendiente m = –2?  determina la ecuación
ii) pasa por Q(–3,6) y tiene pendiente m = 1?
iii) pasa por N(–2,–5) y tiene pendiente m = 4?
h) ¿Cuál de los siguientes puntos pertenece a la recta r) y = –3x + 7 ?
A(–1,10)
i) Representa las rectas
r) y = x
e
s) y = –x
j) Representa las siguientes rectas en un mismo
sistema de ejes. ¿Qué observas?
f:NR
/
g:ZR /
h:QR /
t:RR /
C(0,7)
D( ,8)
¿Qué observas?
r) y = 2x + 2
r) y = 3x + 6
s) y = 8x + 2
s) y = 3x
t) y = –3x + 2
t) y = 3x – 3
k) Indica valores de m y m’ para que las rectas sean paralelas:
l) Traza los gráficos de:
B(2,13)
r) y = mx + 7
e
s) y = m’x – 4
f (x) = 2x + 6
g (x) = 2x + 6
h (x) = 2x + 6
t (x) = 2x + 6
16 En el liceo quieren alquilar ómnibus para ir de excursión y se ponen en contacto con dos empresas para informarse
sobre los precios.
A continuación se muestra un gráfico que representa la tarifa de las dos empresas según los kilómetros recorridos.
Prof. Néstor Larroca
Página 26
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
La empresa A ofrece una tarifa inicial de $600 y $1 por cada kilómetro recorrido.
Si identificamos con una función f al precio ofrecido por dicha empresa, su expresión sería:
f : [0,+)  R
/ f (x) = x + 600
donde la x representa a los kilómetros recorridos.
La empresa B ofrece una tasa inicial de $........ por los primeros ……..km de recorrido y $ ….. por cada kilómetro
extra a partir de los …… km.
¿Qué empresa les ofrece la tarifa más barata si para ir de excursión tienen que recorrer una distancia entre 500km y
700km?
Respuesta: ………………………………………………………………………………………………………
………………………………………………………………………………………………………
Otra empresa C ofrece una tarifa inicial de $400 y $1 por cada kilómetro recorrido. Grafica la tarifa de la empresa C en
el gráfico dado y determina la expresión de una función h que identifique al precio ofrecido por esta empresa.
h : [0,+)  R
/ h (x) = ………………
17 Una función, determinada por una expresión como la que sigue:
f:RR
/ f (x) = 2x2 – 8
es una función de segundo grado, ya que el mayor exponente de la variable x es 2. En alguna bibliografía la encontrarás
con el nombre de función cuadrática.
Visita
http://descartes.cnice.mec.es/materiales_didacticos/funcion_cuadratica_madr/f1.htm
http://descartes.cnice.mec.es/materiales_didacticos/Funcion_cuadratica_parabola/cuadratica2.htm
Genéricamente escribimos  f : R  R
/ f (x) = a x2 + b x + c
En la función f indicada al comienzo del ejercicio indica los valores de:
La función cuadrática es aquélla que asocia a cada número x el número a x2 + b x + c, donde a , b y c son tres valores
fijos.
Las funciones cuadrática se representan mediante parábolas. La parábola intersecará al eje de las abscisas en los valores
de x que sean raíces de la función.
Por ejemplo, si tenemos
f:RR
/ f (x) = 2x2 – 8
Para hallar la raíz:
2x2 – 8 = 0
2x2 = 8
x2 = 4
x=  4
x=2
 Decimos que
x1 = 2 e x2 = – 2 son raíces de f
 Los puntos de coordenadas (2 , 0) y (–2,0) pertenecen al gráfico de f .
La parábola intersecará al eje de las ordenadas en un punto de abscisa cero.
Así que calculamos f (0) tenemos que
f (0) = 2. 02 – 8
f (0) = – 8
Prof. Néstor Larroca
 El punto (0,– 8) 
G( f ).
Página 27
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Observa que -8 es el valor de c en f (x) = a x2 + b x + c
La abscisa del vértice de la parábola se obtiene como la
semisuma de las raíces (cuando las hay!!!).
En este caso
xv=
x1  x 2
2

xv=
2  ( 2)

2
xv= 0
Luego para hallar la ordenada correspondiente al vértice,
calculamos f (x v) que en este caso es f (0) = – 8
Por lo tanto la función f (x) = 2x2 – 8 tendrá por gráfico el
que se indica 
Recordar que dijimos que la expresión general de la función de segundo grado es
f (x) = a x2 + b x + c.
En el caso anterior es a = 2, b = 0 y c = –8.
Cuando a > 0 decimos que la parábola tiene
concavidad positiva y si a < 0 decimos que la
parábola tiene concavidad negativa.
Visita
http://x.edu.uy/cuadratica.htm
Concavidad
Por ejemplo, si tenemos
f:RR
positiva
Concavidad
negativa
/ f (x) = – x2 – 4x
Para hallar la raíz:
– x2 – 4x = 0
x=0
x (– x – 4) = 0 
–x–4=0  x=–4
 Decimos que
x1 = 0 e x2 = – 4 son raíces de f
 Los puntos de coordenadas (0 , 0) y (–4,0) pertenecen al gráfico de f .
La parábola intersecara al eje de las ordenadas en un punto de abscisa cero.
Así que calculamos f (0) tenemos que
f (0) = – 02 – 4 . 0
f (0) = 0
Prof. Néstor Larroca
 El punto (0, 0) 
G( f ).
Página 28
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Observa que 0 es el valor de c en f (x) = a x2 + b x + c
La abscisa del vértice de la parábola se obtiene como la
semisuma de las raíces (cuando las hay!!!).
xv=
En este caso

x1  x 2
2

xv=
0  ( 4)
2
x v = –2
Luego para hallar la ordenada correspondiente al vértice,
calculamos f (x v) que en este caso es:
f (–2) = – (–2)2 – 4 (–2)
f (–2) = – 4 + 8
f (–2) = 4
Por lo tanto la función f (x) = – x2 – 4x tendrá por gráfico
el que se indica 
18 a) Dada d: R  R / d(x) = –x 2 + 9, halla raíces, calcula d(0) y realiza un bosquejo gráfico de la función.
b) Dada g: R  R / g(x) = 3x 2 – 3x, halla raíces, calcula g(0) y realiza un bosquejo gráfico de la función.
c) Halla el, o los valores de x para que d(x) = –16
19 Observa y completa la secuencia:
Figura
Prof. Néstor Larroca
Lugar
Medida del
lado
Cantidad de
cuadraditos
1
1
1 = (2 1 – 1)2
2
3
9 = (2 2 – 1)2
3
5
25 = (2 3 – 1)2
4
7
49 = (2 4 – 1)2
Página 29
Liceo La Paz 2
Año 2013
…
…
Matemática 3er año: Funciones
…
…
n
Cuando nos piden desarrollar un polinomio lo que debemos hacer es efectuar las multiplicaciones o potenciaciones
indicadas.
Por ejemplo desarrollar el polinomio A(x) = 3(x – 2) es expresarlo como A(x) = 3x + 6 (hemos aplicado la propiedad
distributiva en el sentido de desarrollar).
Para desarrollar el polinomio B(x) = 5x (2x – 1) lo expresamos como B(x) = 10x2 – 5x
Otros ejemplos:
i) C(x) = (5x – 4)(3x + 2) lo expresamos como C(x) = 15x2 + 10x – 12x – 8
Esta expresión del polinomio C a su vez se puede reducir. Cuando nos piden esto, lo que debemos
hacer es sumar los términos semejantes.
Así el polinomio C(x) = 15x2 + 10x – 12x – 8
C(x) = 15x2
– 2x
–8
ii) D(x) = (3x + 2)2 lo expresamos como D(x) = 9x2 + 12x + 4
Hay multiplicaciones especiales que conviene recordar:
Para desarrollar (3x + 2)2 tuvimos en cuenta el desarrollo del cuadrado de un binomio.
Así (3x + 2)2 = (3x)2 + 2.3x.2 + 22 = 9x2 + 12x + 4
Si te resulta engorroso tener que recordar la “fórmula” de la expresión puedes resolverlo aplicando
propiedad distributiva en el sentido de desarrollar y luego reducir.
Así (3x + 2)2 = (3x + 2)(3x + 2) = 9x2 + 6x + 6x + 4
D(x) = 9x2
+ 12x
+4
Actividad 1
Desarrolla los siguientes polinomios:
P(x) = (7x + 5)2
Q(x) = (4x – 8)2
R(x) = (9x + 11)( 9x – 11)
La propiedad distributiva la podemos aplicar en el sentido de desarrollar o de factorizar.
Prof. Néstor Larroca
Página 30
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Cuando se nos pide factorizar un polinomio debemos expresarlo utilizando la operación multiplicación.
Recuerda la expresión que debiste obtener al comienzo de este ejercicio 19
 (2n – 1)2
Al desarrollar esta expresión se obtiene (2n – 1)2 = 4n2 – 4n + 1
Ahora si te piden factorizar la expresión 4n2 – 4n + 1 debes escribir 4n2 – 4n + 1 = (2n – 1) (2n – 1)
Para poder factorizar expresiones como la anterior, debes primero “practicar mucho” el desarrollo de cuadrados de
binomios…de otra forma resultará dificultoso que te des cuenta.
Otras expresiones se pueden factorizar más fácilmente. Por ejemplo si tienes 9x2 + 12x puedes tener presente que esta
expresión polinómica la puedes escribir como:
9xx + 12x
Observa que el factor x es común a ambos términos, se dice que es factor común. Este factor común lo escribimos
“fuera” del paréntesis y “dentro” del paréntesis escribimos el resto de la expresión, resultando:
9xx + 12x = x(9x + 12)
También sería correcto factorizar así:
3.3xx + 3.4x = 3x(3x + 4)
Actividad 2
Para factorizar un polinomio “usando cuadrado de un binomio” analizamos en primer lugar, si puede
tratarse de un desarrollo de cuadrado de binomio. Por ejemplo:
Extraído del libro Matemática 3 de C. Ochoviet
y M. Olave – Ed. Santillana
Entonces, podemos escribir que:
9x2 + 24x + 16 = (3x + 4)2
Factoriza tu estos otros polinomios:
a) 9x2 + 6x + 1 =
b) 4y2 – 20y + 25 =
c) 81x2 – 180x + 100 =
d)  + x + x2 =
e) 5m2 – 10m + 5 = 5 (…. – ….)2
Aquí tienes ayuda!!!
Actividad 3
Para factorizar un polinomio “usando producto de binomios conjugados” analizamos, en primer lugar, si
el polinomio puede tratarse del producto de dos binomios conjugados. Por ejemplo:
Extraído del libro Matemática 3 de C. Ochoviet
y M. Olave – Ed. Santillana
Prof. Néstor Larroca
Página 31
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Entonces, podemos escribir que:
25x2 – 49 = (5x + 7) (5x – 7) o también 25x2 – 49 = (–5x + 7) (–5x – 7)
Factoriza tú, estos otros polinomios:
a) 9x2 – 4 =
b) 49 – a2 =
Actividad 4
Extrae factor común en estas expresiones polinómicas:
a) –3x2 + 6x =
b) –x2 + x =
c) –10x2 + 8x3 =
d)  m2 + m3 =
e) 5x(x +1) + 5x(x – 2) =
f) (3x +1)(–5 x +1) + (3x +1)(8x – 2)
20 Desarrolla, reduce, halla raíces y realiza bosquejo gráfico de:
a) a: R  R / a(x) = (2x + 8)2 – 32x – 80
b) b: R  R / b(x) = (5x – 3)2 + 30x – 23x2 + 1
c) c: R  R / c(x) = -3(x + 2)(x – 2) + 7(x – 3) + 2x2 – 7x
d) d: R  R / d(x) = (x + 5)2 – 25 –10x + x2
21 Cada gorila trata de pegarle al otro tirándole una banana.
El gorila Maguila (A) a tirado una banana al gorila
Mardilla (B) y ésta recorrerá una curva cuya ecuación es:
y = – x 2 + 8 x – 7.
a) Grafícala y averigua si dará en el blanco.
b) ¿Cuál es la máxima altura que alcanzará la banana?
22 Una pelota es lanzada hacia arriba con una velocidad inicial de 20 pies por segundo. Las distancia en pies desde el
suelo es una función de tiempo definida por f: R  R / f(t) = –5t 2 + 20t donde f(t) es la distancia y t es el tiempo
en segundos.
a) Encuentra la altura máxima que alcanzó la pelota.
b) ¿Cuándo alcanzará la pelota esta altura?
c) ¿Cuándo caerá la pelota al suelo?
Prof. Néstor Larroca
Actualmente el «pie» se utiliza sólo como unidad de medida popular en
los países anglosajones de Estados Unidos, Canadá y Reino Unido, y
todavía se emplea en aeronáutica (incluso fuera de los países
anglosajones) para expresar la altitud de aviones y otros vehículos
aéreos.
Es usual utilizarlo para longitudes de hasta unos tres metros (aunque hay
excepciones como observarás en este ejercicio). Para longitudes mayores
se suele emplear la yarda o la milla. Un pie equivale a 30,48 cm
Página 32
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
23 Determinar entre los rectángulos de perímetro 24cm., él o los rectángulos de mayor área.
y
x
P = 2 (x + y )
 2 (x + y ) = 24 
x + y = 12  y = 12 – x
 Á = x (12 – x )
P = 24
 Á = ………………..
Á = x .y
a) Grafica la función determinada por la expresión que obtengas para el área.
b) ¿Para que valor de x se presenta un máximo en la función?
24 a) Se te informa que la función f : R  R / f (x) = –2x2 +2x + 12 tiene raíces
del vértice y realiza un bosquejo del gráfico.
b) Se te informa que la función g : R  R / g (x) = x2 – 2x – 8 tiene raíces
del vértice y realiza un bosquejo del gráfico.
c) Dada la función h : R  R
x1 = –2 y x2 = 3 halla coordenadas
x1 = – 2 y x2 = 4 halla coordenadas
/ h (x) = – 2x2 + 18 i) Halla raíces.
ii) Halla h (  ) , h (–1).
iii) Dibuja el gráfico de la función.
d) Dada la función t : R  R
/ t (x) = 3x2 – 15x
i) Halla raíces.
ii) Halla t (  ) , t (–1).
iii) Dibuja el gráfico de la función.
25 En el ejercicio anterior se te informa que las raíces de función
f : R  R / f (x) = –2x2 + 2x + 12 son
x2 = 3. Seguro tu curiosidad será saber como llegar a saber las raíces de esta función sin que te lo digan.
x1 = –2 y
Para hallar las raíces de la función deberás plantear una ecuación:
–2x2 + 2x + 12 = 0
Una ecuación de segundo grado es de la forma:
ax2 + bx + c = 0 con a  0.
Para despejar la x se sigue un largo y complicado proceso que no vamos a ver en el curso. El resultado final es la
siguiente fórmula, que deberás intentar memorizar, pues la usarás infinidad de veces en tus cursos de Matemática.
SOLUCIONES DE
SEGUNDO GRADO
UNA
ECUACIÓN
DE
El doble signo () quiere decir que hay dos soluciones:
 b  b 2  4ac
x1 
2a
Practiquemos la fórmula resolviendo
Entonces,
x
– 2x2 + 2x + 12 = 0 donde
a = –2,
y
b=2
 b  b 2  4ac
x2 
2a
y c = 12
 2  2 2  4.(2).12
Prof. Néstor Larroca
2.(2)
Página 33
Liceo La Paz 2
Año 2013
x
 2  4  96
4
x
 2  100
4
x
 2  10
 2  10
de donde se tiene que x1 
4
4
x1 = –2
Por lo tanto las raíces son
La función
f:RR
y
x2 = 3
Matemática 3er año: Funciones
y x1 

 2  10
4
S = {–2,3}
/ f (x) = –2x2 + 2x + 12
tendrá pues un gráfico como el que se muestra
Para hallar las coordenadas del vértice
 xV   2   2  1
2.(2)
4
2
La ordenada del vértice la hallamos sustituyendo el valor
de x hallado en la expresión de la función.
f () = –2()2 + 2.  + 12

f () =
25
2


f () = –  + 1 + 12
f () = 12,5
Por lo tanto el vértice tiene coordenadas
V ( 1 , 25 )
2 2
Se dice que en x =  hay un máximo de la función.
Nota:
Las dos raíces de la ecuación pueden en algún caso ser iguales o no existir en los números reales.
En la ecuación x2 – 6x + 9 = 0 es a = 1
b = –6
y c=9
Entonces,
x
 (6)  (6) 2  4.1.9
Prof. Néstor Larroca
2.1
Página 34
Liceo La Paz 2
Año 2013
x
6  36  36
2
x
6 0
2
x
6  0 de donde se tiene que
60
x1 
2
2
Por lo tanto las raíces son
x1 = 3
y
y x1 
Matemática 3er año: Funciones
60
2
x2 = 3.
En este caso se dice que la ecuación tiene raíz doble.
La función
xV 
f:RR
/ f (x) = x2 – 6x + 9 tendrá pues un gráfico como el que se muestra.
 (6) 6
  3  f (3) = 32 – 6.3 + 9  f (3) = 0
2.1
2
Entonces el vértice es V (3,0)
Se dice que en x = 3 hay un mínimo
de la función.
En la ecuación –x2 + 3x – 3 = 0 es a = –1
Entonces,
x
b=3
y
c = –3
 3  3 2  4.(1)(3)
2.(1)
x
 3  9  12
2
x
3 3
2
Y no avanzamos más pues
 3  R ya que  a  R  a2 = – 3
Por lo tanto las raíces no son números reales.
En este caso se dice que la ecuación tiene raíces imaginarias.
Prof. Néstor Larroca
Página 35
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
La función f : R  R / f (x) = –x2 + 3x – 3 tendrá pues un gráfico como el que se muestra y al no existir raíces
reales el gráfico NO INTERSECA al eje de las abscisas.
En este caso es
xV 
3
2(1)

xV 
2
Luego

3
 3
 3
f       3.  3
2
 2
 2
 3   9 18 12 
f 
 
4 4
 2 4

3
2
9 9
3
f      3
4 2
2
 3 3
f 
2 4
Se dice que en x = 3/2 hay un máximo
de la función.
La expresión
 = b2 – 4ac se llama discriminante de la ecuación. El número de soluciones depende del signo de .
Halla tú ahora las raíces de las siguientes funciones de segundo grado y realiza un bosquejo de su gráfico.
a) a : R  R
/ a (x) = x2 – x – 30
b) b : R  R
/ b (x) = 18x2 + 3x – 3
c) c : R  R
/ c (x) = 2x2 + 9x + 4
d) d : R  R
/ d (x) = –2x2 – 12x – 10
e) e : R  R
/ e (x) = 5x2 – 2x + 1
f) f : R  R
/ f (x) = 4x2 + 20x + 25
Curiosidades, problemas, ejercicios
i) Para evaluar la necesidad de semáforos en un cruce de calles, entre las 3 de la tarde y las 10 de la noche de un día, se
coloca un contador de autos. Los resultados del estudio vienen dados por la expresión:
a = (2h – 6)(18 – 2h)
donde a representa el número de autos que pasaron por el cruce en una hora h del día.
a) ¿Cuántos autos pasaron a la hora 5? Plantea los cálculos necesarios.
b) Calcula cuántos autos pasaron a la hora 3 y a la hora 9. Plantea los cálculos necesarios.
c) ¿A qué hora no pasó ningún auto? ¿Por qué?
ii) ¿Son 3 y 4 las raíces de la ecuación
x2 – 7x + 12 = 0?
Explica tus respuestas. Realiza los planteos que sean necesarios.
iii) ¿Son 2 y -6 las raíces de la ecuación
(3x – 7)(2x + 12) = 0?
Explica tus respuestas. Realiza los planteos que sean necesarios.
iv) Escribe una ecuación que tenga por raíces 5 y –1.
Prof. Néstor Larroca
Página 36
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
v) Entre los métodos de resolución de ecuaciones desarrollados por los hindúes, está el método de inversión, que consiste
en “desandar lo andado”, o sea realizar todas las operaciones en orden inverso. Uno de sus problemas decía:
“Si entendiste bien el método de inversión, dime, hermosa niña de ojos radiantes, ¿cuál es el número que multiplicado
por 3, aumentado en las ¾ partes del producto, dividido después entre 7 y disminuido en 1/3 del cociente, multiplicado
pos sí mismo, restándolo 52, extrayendo la raíz cuadrada, sumándole 8 y dividiéndolo por 10, da el número 2?”
Tener presente que si a un número se lo aumenta en sus ¾ partes, es lo mismo que decir que al número se lo multiplica
por 7/4, decir que a un número se lo disminuye en un 1/3, es lo mismo que decir que se lo multiplica por 2/3 y decir que
a un número se lo multiplica por si mismo es lo mismo que decir que se le eleva al cuadrado. La respuesta que debes
obtener es 28, ve como llegas a él.
vi) El producto de un número entero por su siguiente es 272. Calcúlalos.
vii) Si al cuadrado de un número positivo le quitas su doble, obtienes su quíntuplo. ¿Cuál es ese número?
viii) Ejercicio extraído del libro Matemática 3 de C. Ochoviet y M. Olave de Editorial Santillana
Se te muestra a continuación una forma posible de analizar un caso (no olvides además atender la concavidad)
Prof. Néstor Larroca
Página 37
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Ejercicios de la profesora Sandra Fernández.
Ejercicios para realizar con GeoGebra
a) Considera las siguientes funciones: f (x) = 0,5x2
g (x) = x2
h (x) = 3x2
¿Qué tienen en común todos los gráficos? ¿En qué se diferencian?
¿Qué pasa con el valor de 1a imagen cuando x se hace arbitrariamente grande en valor absoluto?
¿Dónde crees qué se situaría el gráfico de t (x) = 2x2 respecto a los otros?
b) Considera ahora las funciones:
f (x) = –0,5x2
g (x) = –x2
h (x) = –3x2
¿Sabrías obtener sus gráficas a partir de las gráficas ya representadas en la parte anterior?
¿Mediante qué, transformación geométrica?
¿Qué pasa con el valor de la imagen cuando x se hace arbitrariamente grande en valor absoluto?
¿Cómo influye el signo y el valor absoluto del coeficiente “a” en el gráfico de f (x) = ax2?
c) Representa ahora, en una a pantalla, las siguientes funciones: f (x) = x2
h (x) = x2 – 2
g (x) = x2 + 3
Explica la influencia de los términos +3 y –2 en los gráficos.
¿Puedes generalizarlo para
f (x) = x2 + q dónde q es un número real cualquiera?
d) Representa ahora, en una a pantalla, las siguientes funciones: f (x) = x2
g (x) = (x + 3)2
h (x) = (x – 2)2
Explica la influencia de los términos +3 y –2 en los gráficos.
¿Puedes generalizarlo para
f (x) = (x + p)2 dónde p es un número real cualquiera?
e) Se considera la función
f (x) = (x – p)2 + q
donde p y q son números reales.
Siendo q = -4 represéntala para p = -4 , p = 0 y p = 3 ¿en qué se parecen y en qué se diferencian los gráficos?
Siendo p = -4 represéntala para q = -4 , q = 0 y q = 3 ¿en qué se parecen y en qué se diferencian los gráficos?
f) Considera las funciones:
f (x) = x2 – 3x – 2
g (x) = x2 – 3x – 0,5
h (x) = x2 – 3x + 1
t (x) = x2 – 3x + 5
Represéntalas en una misma pantalla.
¿Cómo influye el valor del término independiente? ¿En qué se parecen los gráficos? ¿En qué se diferencian?
Observa la pospón de los vértices de cada una de las parábolas, ¿crees que todos tienen la misma abscisa?
g) Considera ahora f (x) = x2 –4x+2
g (x) = x2– 2x+2
h (x) = x2+2
t (x) = x2 +2x+2
j (x) = x2 +4x+2
Representa las 5 parábolas en un mismo sistema de ejes.
¿Mantienen todas la misma forma?
¿Crees que se podrían superponer unas sobre otras mediante traslaciones?
¿Te animarías a hacer alguna conjetura sobre la posición del vértice de la parábola correspondiente a
f (x) = ax2 + bx + c, cuando varía b, manteniendo constantes a y c?
h) Representa las funciones f (x) = 0,4x2 – 3x +2
g (x) = x2 – 3x +2
h (x) = 3x2 –3x +2
j (x) = 5x2 –3x +2
¿Cómo influye el valor del coeficiente de x2 sobre la forma de los gráficos de las funciones?
¿Mantienen todas la misma forma?
¿Cómo invertirías la concavidad, manteniendo la forma?
Representa en el mismo sistema de ejes las funciones k (x) = –3x2 – 3x + 2 y d (x) = –5x2 +3x –2
¿Sabrías hacer alguna conjetura sobre la posición del vértice de la parábola correspondiente a f (x) = ax2 + bx + c,
cuando varía a, manteniendo constantes b y c?
Prof. Néstor Larroca
Página 38
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
26
La generación de energía eólica se considera como una fuente de energía que puede
sustituir a los generadores de electricidad alimentados por petróleo y carbón. La
rotación de las aspas de los molinos de viento acciona los generadores que producen
energía eléctrica.
Las siguientes gráficas muestran la velocidad promedio del viento en cuatro lugares
diferentes a la largo de un año.
¿Cuál de las gráficas indica el lugar más apropiado para poner un generador de energía
eólica?
¿Estos gráficos pueden corresponder a los de alguna función?
Cuánto más viento hay, más rápido rotan las aspas del molino de viento y así se genera más energía eléctrica. Sin
embargo, en un entorno real la relación entre la velocidad del viento y la energía eléctrica generada no es directa (o sea
que si por ejemplo, aumenta al doble la velocidad del viento, no aumenta necesariamente al doble la energía eléctrica
generada).
A continuación se plantean las condiciones de funcionamiento de la generación eólica en un entorno real.
 Las aspas empezarán a rotar cuando la velocidad del viento sea v 1.
 La energía alcanzará un valor w cuando la velocidad del viento sea v 2.
 Por razones de seguridad, la rotación de las aspas no aumentará cuando la velocidad del viento sea mayor que v 2.
¿Cuál de las siguientes gráficas representa mejor la relación entre la velocidad del viento y la energía eléctrica generada
en estas condiciones?
¿Estos gráficos pueden corresponder a los de alguna función?
27 Bolsas de azúcar
Cada punto de este gráfico representa una bolsa de azúcar.
a) ¿Qué bolsa es la más pesada?
b) ¿Qué bolsa es la más barata?
c) ¿Qué bolsas tienen el mismo peso?
d) ¿Qué bolsas tienen el mismo precio?
e) ¿Qué bolsa sale mejor de precio: F ó C? ¿Por qué?
f) La relación que establece el precio de una bolsa en función del peso, ¿es función?
Prof. Néstor Larroca
Página 39
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
28 La familia
En el gráfico de abajo tenemos una fotografía de la familia López: Juan es el abuelo, los hijos de Ana y José son Pablo
que va a la guardería, Pepe está estudiando 3º de liceo, Alicia que estudia medicina y Luis es el recién nacido.
a) ¿Quién está representado por cada uno de los puntos del diagrama de la derecha?
b) ¿Es apropiada la asignación de magnitudes que se ha hecho a cada eje?
c) Realiza una representación de toda la familia donde representes en el eje horizontal la edad y el eje vertical la altura
de cada uno de ellos.
29 Bolas
Si A y B representan bolas de distinto material y tamaño, a la vista de los diagramas, indica si son ciertas o falsas las
afirmaciones siguientes:
Nota: Elige el diagrama adecuado a la vista de las magnitudes que vayas a comparar en cada caso.
a) La que tiene más volumen, tiene más peso.
b) La que tiene menos peso, tiene más volumen.
c) La que tiene más peso, cae más rápidamente.
d) La que tiene más volumen cae más rápidamente.
Prof. Néstor Larroca
Página 40
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
30 Dados azules y rojos
Vamos a lanzar un par de dados sobre una mesa, uno azul y otro rojo
y sumaremos sus resultados. Podemos representar los lanzamientos
situando un punto en la trama:
a) ¿Qué representa el punto marcado?
b) Representa los posibles resultados de obtención de 8.
¿Qué se observa gráficamente?
¿Es correcto unir los puntos obtenidos?
31 Consumo de combustible
El gasoil que hay en un depósito de un autobús viene representado por la siguiente gráfica:
a) ¿Cuántos litros tenia el depósito al salir?
b) ¿Cuántos litros tenia a su llagada?
c) ¿Cuándo puso el conductor por primera vez gasoil? ¿Cuántos litros tenía el depósito?
d) ¿Cuántos litros consumió durante el viaje?
e) ¿Qué ocurrió en el km. 250? ¿Se pueden unir los puntos A y B y los puntos C y D?
32 Paseo de dos amigos
Rafa y Alicia son compañeros de clase y quedan un día para salir. Rafa sale de su casa y recoge a Alicia, que tarda un
poco en bajar. Después dan un paseo y se sientan en una cafetería a tomar un refresco. Al regreso se acercan a casa de
unos compañeros a recoger unos apuntes y allí se entretienen un tiempo. Después regresan a casa. La gráfica del paseo
viene aquí representada.
a) ¿Qué variables se relacionan?
b) ¿Cuál es la variable dependiente y la variable
independiente?
c) ¿Cuánto dista la casa de Alicia de la de Rafa?
d) ¿Cuánto tiempo esperó Rafa a que bajara Alicia?
e) ¿Cuánto tiempo tardaron en llegar a la cafetería?
f) ¿A qué hora salieron de la cafetería?
g) ¿A qué casa regresaron?
h) ¿Cuánto tiempo pasearon los dos juntos?
Prof. Néstor Larroca
Página 41
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
i) ¿Cuándo pasearon más deprisa: de la cafetería a casa de sus amigos o de ésta al final del paseo? ¿Por qué?
j) Inventa una historia para la gráfica siguiente
33 Relaciona cada una de las siguientes botellas con su correspondiente gráfico obtenido al ir llenándose las mismas.
Visita
http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/03-2-u-graficas.html
34 Considera la función f : R  R
/ f (x) = h(mx + n)2 + px + q
h
1
2
–3
m
1
1
1
n
0
4
–5
p
0
–12
–45
q
–4
–62
117
Desarrolla y reduce la expresión de la función f para los distintos valores que se hallan en las filas de la tabla.
Prueba en Geogebra dejar 4 valores fijos e ir cambiando uno solo de los 5 para observar que ocurre con el gráfico de la
función.
35 Trabajaremos con Geogebra. En la línea de Entrada ingresa 1.
Al dar Enter observarás en la Vista Algebraica que se ha creado el número a.
Prof. Néstor Larroca
Página 42
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Repite lo mismo dos veces más.
Se crearán así tres números a, b y c. Ahora haz clic derecho
sobre algunos de estos objetos libres en la Vista Algebraica
(por ejemplo sobre b) y se despegará un menú contextual,
en el que elegirás la opción Propiedades.
Se abrirá un cuadro de diálogo de Propiedades donde iremos eligiendo en la solapa Básico, para cada uno de los tres
números, la opciones Muestra Objeto y Muestra Rótulo (Nombre y Valor):
Este procedimiento hace que aparezcan tres deslizadores alineados.
En la línea de Entrada ingresa a x2 + b x + c.
En la expresión anterior, no hay que omitir el espacio entre "a" y "x", y entre "b" y "x", pues tal espacio es el operador
de multiplicación (equivale a *). Si se omite, GeoGebra consideraría "ax" y "bx" como variables no definidas. Por otra
parte, si en vez de los parámetros a, b y c colocamos números concretos, como por ejemplo 3x2 + 5x +2 podríamos
omitir el operador multiplicación, pues GeoGebra sólo puede interpretar "3x" como un producto, nunca como el
nombre de un objeto (los nombres siempre comienzan con una letra).
Prof. Néstor Larroca
Página 43
Liceo La Paz 2
Año 2013
Al dar Enter observarás que en la vista gráfica aparece el gráfico de f : R  R
de a, b y c son 1
Matemática 3er año: Funciones
/ f (x) = x2 + x + 1 ya que los valores
Con la herramienta texto hacemos clic en un lugar vacío de la Vista Gráfica y al arrastrar el ratón aparecerá un cuadro
de dialogo donde deberás digitar el texto "f(x) = " + f
Con la herramienta Elige y mueve los parámetros a, b y c (desde los puntos que aparecen en los deslizadores)
observando en cada caso cómo afectan sus cambios a la gráfica de la función, particularmente el signo de cada uno.
Prof. Néstor Larroca
Página 44
Liceo La Paz 2
Año 2013
Matemática 3er año: Funciones
Investigación:
• ¿Qué trayectoria describe el vértice de la parábola al variar b?
Crear el vértice, para ello ingresa en la línea de entrada Extremo[f], activa su Rastro y desplaza b.
• ¿Qué sucede con las funciones cuadráticas definidas como g (x) = a x2 + a x + a? Probar a activar el rastro
de cada una de estas funciones antes de mover el deslizador "a".
Cuando ingreses la expresión de g desactiva la de f.
• Realiza pruebas con el comando Raíz[f]. Ingresa esto anterior en la línea de entrada.
Para conocer la sintaxis de cada uno, basta introducir su nombre en el campo de Entrada y pulsar F1.
36
Prof. Néstor Larroca
Página 45