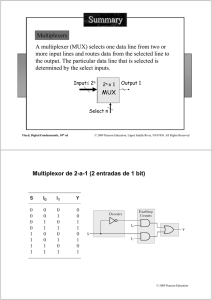
342176961-236267023-Steel-Structures-5th-Edition-Solutions-Manual-pdf

#$%
"
"
&'" "
( '
,-,# - " " .
"
$
)"
"
"
7
)) &" * "
"
! / 0 #1 "
$<
"
9 6$?2 !
"
"
9
/ 0
#1 "
"
+
)"'
"
'
)"
"
)
/*0 234 5
26 "
"
+
)"'
9 %$4 B %$1 9 %$4 B %$1/# 0 9 1$6
9%$1 9 442 1 9 #3$2 =&
"
'
)
9 #3$2 B%%4 9 %26 =&
7
9 6$:6/2601$:- 9 #%4 =&
"
)"
7
9 6$32/1202$:6 9 4?? =&
7
)
)
B
$
!! )"
"
)"
"
A
'
)"
9
"
7
'
9
@
"
)"
9# 9 #/#3$20 9 %%4 =&
"
"
= .
;$ #$2$4$
$
7
9
)
9
'
'
96$32/2?02$:6 9 423 =&
7
)
"
"
!.
* ) &'"
"" )
9 6$:6/#101$:- 9 442 =&
!! )"
9
"
)
9 6$?2/1$:-0 9 2$:6 ; $
)"
9
"
"
$
$
@
!"
9 1$:- ; $8 ( 9 %$63
1 , - , # -8
&'" "
!! )"
')"
) !!) "
)
> ' " & )" )
) * " " +* & )
"
' "& " $
/*0 234 5
26 " $
'
9%$4 B %$1
'
9%$-
"
A
9 $4 B %$1/# 0 9 1$6
9 " 1 9 4?? 1 9 -3$: =&
9 # 9 #/-3$:0 9 %-- =&
9 B 9 -3$:B %-- 9 %:4 =&
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$4
* " $
"
"
#$#
&'" "
* % -C $( %4 $
42F
&'" "
( ' )) &" * "
)
" " +* & )
)"
* "
$
-C $
) "
1,-,# - " " )
* "
" 1C $
) "
'*
!3 ?C $C
!3 ?C $C
'
"
>
" " * " & ")& "
) + "
$
"
$
! / 0 #1 "
/*0 234 5
26 "
)"
1 , - , # -8
7
&'" "
" * "
" =
!! )"
!
9 %$6$
9
9 1$:- ; $8 ( 9 %$63
$<
"
>"
"
')"
)
"
!!)
"" )
"
"
C -! )
&'" "
$
" !
"
"
)
+
* "
*
)
)"
9
"
)
)
"
"
"
06$42 9 4$32 ; $
9 %$66/4$320 9 4$32 ; $
> &%C-1
)" 7
9 6$:6/#101$:- 9 442 =&
+
!! )"
" )"
9 6$32/2?0-$1: 9 46- =&
"
'
7
B %$1 9 %$4 B %$1/# 0 9 1$6
' 9 %$4
' 9 %$9 " 1 9 46- 1 9 #- =&
9# 9 #/#-0 9 %64 =&
)
9 B 9 #- B%64 9 %#1 =&
26 "
!!)
$
9 %$66/-$1:0 9 -$1: ; $
#1 "
)
)
)
"
06$32 9 -$1: ; $
' > E' '
#1 " >
@
9 "
"
)"'
9 "
"
)"
')"
!! )"
$
"
B 0" 9 6$42/%40 C %/6$:#32 B
D/
9
B 0" 9 1$:- C #/6$:#32 B
#1 " & " "
)"
!
'
$
D #$# !
$
"
9
D #/
/*0 234 5
@
)"'
9
"
)"
" $
" "
* "
D
D#
9
/ 0
)) &" *
)
*
!
&
32F
>
3 ?C $
!! )"
9 %$6$
"
9
( '
"
"
A
9 6$:6/#10/#$660 9 :3$4 =&
!! )"
" )"
9 6$32/2?04$32 9 %46 =&
'
7
B %$1 9 %$4 B %$1/# 0 9 1$6
' 9 %$4
' 9%$9 " 1 9 :3$4 1 9 %1$4 =&
9# 9 #/%1$40 9 -?$1 =&
)
9 B 9 %1$4 B-?$1 9 1-$? =&
.
& ) & " '
A
)
)
!"
"
"
"
+
C -$%>
"
!
9 6$?2/#$660 9 4$22 ; >
)"'
9 4$32 ; $
)"'
!! )"
" )" 7
9 " ' 9 6$32/2?04$22 9 %%% =&
"
"
" ) "
*+ +
)" $
"
)
9 B 9 %1$4 B -?$1 9 1-$? =&
(
>
)"
7 " 9 " + 9 6$:6/2601$:- 9 #%4 =&
!! )"
" )" 7
9 6$32/120-$1: 9 44: =&
"
A
'
7
B %$1 9 %$4 B %$1/# 0 9 1$6
' 9 %$4
' 9 %$9 " 1 9 44: 1 9 #?$% =&
9 # 9 #/#?$%0 9 %%- =&
)
9 B 9 #?$% B %%- 9 %24 =&
>
9
"
)"'
9
"
)"
9 6$?2
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
A
#$* " "
' !
"
&'" "
"
"
)
.
%# %1C $
! " & " / )
0 . " ))
#1 "
' >"
" $
&'" "
!! )"
9 %$6$
"
$
"
)"
& +
')"
" ))
"
C -'
!' $
) &'" "
( '
!' "
"
" ' >
)
!!)
"
"
#$2
&'" "
"
"
9 6$?2
9 6$?2/#$320
9 #$%: ; $
)"
9
%C# /
C4
"
)"
9
07
9 #$32C4/6$?%42 B 06$#32
9 #$6: ; $
& " 7
)"
%C4C# . " ". "
B4 "
9 C#
"
% C 4 9 44 G-/40H 9 6$26 $
"
4 C # 9 44 G-/-0H 9 6$42 $
9#$32CG#/6$?320C6$26C6$42H6$#32
9 #$62 ; $
'
' >
"
& " 7
)"
%C-C# . " ". "
B4 "
9 C#
"
C- 9 4$24 G-/40H 9 6$3?% $
"
-C# 9 4$24 G-/-0H 9 6$#:% $
A
)"
9 6$:6/#10/#$320 9%44 =&
9 6$32/2?0#$62 9 %#2 =&
" '
9 %44 =&
"
"
7 ' 9 %$4 B %$1 9 %$4 B %$1/- 0 9 3$1
' 9 %$9 " 1 9 %44 3$1 9 %1$6 =&
9 - 9 -/%1$60 9 1-$6 =&
)
9 B 9 %1$6 B 1-$6 9 ?6$6 =&
!! )"
)"
)
)
"
7
"
"
)"
9
7
')"
)
!!)
"
"
"
+
"
%C# /
C4
"
07
A
& " 7
%C-C# . " ". "
B4 "
"
%C- 9 4$24 G-/40H 9 6$3?% $
"
-C# 9 4$24 G-/-0H 9 6$#:% $
9#$32CG#/%$660C6$3?%C6$#:%H6$#32
9 #$61 ; $
)"
9
>
)"'
>
"
& " 7
)"
%C4C# . " ". "
B4 "
9
C#
"
% C 4 9 44 G-/40H 9 6$26 $
"
4 C # 9 44 G-/-0H 9 6$42 $
9#$32CG#/%$660C6$26C6$42H6$#32
9 4$:% ; $
'
' >
"
9 #$:- ; $
@
!! )"
9 %$6$
.
! " & " / )
)"
"
"
0
. " )) & + ! ' $
234 5
16 "
' >"
%2 %1C $
" $
9 #$32C4/6$:#32 B 0 6$#32
9 #$66 ; $
9#$32CG#/6$?320C6$3?%C6$#:%H6$#32
#1 "
"
"
9/6$#320%6 9 #$32 ; $
(
9 6$?2
9 6$?2/#$320
9 #$%: ; $
9 /6$#320%6 9 #$32 ; $
(
& " I *$ #$-$
&'" "
* " "
"
D -'
( '
' !
)
) &'" "
"
>
"
!' "
))
9
#1 "
@
C#
>
)"
)"'
)"
9 6$:6/160/#$320 946# =&
9 6$32/3204$:% 9 %1- =&
" '
9 %1- =&
"
"
7 ' 9 %$4 B %$1 9 %$4 B %$1/- 0 9 3$1
' 9 %$)
9 " 1 9 %1- 3$1 9 4%$2 =&
9 - 9 -/4%$20 9 ?1$6 =&
)
9 B 9 4%$2 B ?1$6 9 %6? =&
"
)
!! )"
7
"
"
)"
9
7
"
+
"
9
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$1
)" &
!
" '&& " "
/ 0! " )
*+ "
" ')" $
& " * )=C" C* )= # ?C $ *+ )
)"
'
)
)"
.
$
' "
)
"
()
#66$
%8
)
+
&&
9 36 =& 8
7
'
'
"
@
9
9
"
"
"
)"
9 46 !"$
"
"
9
'
!
9
9 #$22 ; $8
4 C-,# , 8
9#$1# ; $8
9#4$-
/+
9 #3$6
/! )"' 0
7
"
@
9
9 6$?
(
(
9 6$:4
9%$43
" 7
+
+
9%$-6
9%$2-
$
9
9%$63
$8
$
J
9%$?2
$
J
"
9
4 C-,# , 8
)
8
9 #6 !"$
)
)"
$ #$#$
C
)"
" ""
"
"
$
"
$
9 6$:6/#10
+
9 6$32/2?0/6$?20
'
)
"
"
9
9
! + "
" *
9
!
9#4$-
/+
0
9 #3$6
/! )"' 0
A
9 #$-: ; $
9
'*
9 #$1# ; $8
9 %$4
$
)"
(
9%$43
$8
+
9%$2-
$
(
9%$14
$8
+
9%$4%
$
* )=C" C* )=0
4 C2,# , 8
9 #$?? ; $8
J
* )= D " D * )=0
C 4 C-,# , 8
9#$1# ; $8
* '" %F '
+
"
)"
'
/
* )= D " D * )=0
"
!"
A
/
(
9
"
'
$8
$8
'
;'
$
"
9 %$4 B %$1 9%$4/120 B %$1/440 9 %%# =&
9 %$-/120 9 :% =&
'
)"
9 #$1# ; $8
4 C#,#,
)"
/ 0
' "
"& " >
9 44 =& 8 #1 "
" *
')" >
8 9 6$?2 ))
! * " * "
.
"
* )= D " D * )=0
C 4 C-,# , 8
&&
9 12 =& 8
0
9 #$2? ; $
'*
4 C#,#, 8
"
)
+
A
9
! + "
' " *
4 C-,# , 8
47
$
9 6$:6/#10
+
)
;'
/
)"
"
)
)"
$ #$#$
C
)
" ""
"
"
8
$
"
9 6$32/2?0/6$?20
'
!"
/
9
#$1
)" &
!
" '&& " "
/ 0! " )
*+ "
" ')" $
& " * )=C" C* )= # ?C $ *+ )
)"
'
)
)"
.
$
' "
"
()
#66$
9 %$4 B %$1 9%$4/360 B %$1/460 9 %%1 =&
9 %$-/360 9 :? =&
" 7
"
"
& " >
9 46 =& 8 #1 "
" *
')" >
8 9 6$?2 ))
! * " * "
.
)"
/ 0
'
9 #$1# ; $8
* )=C" C* )=
"
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$1
)
)
)" &
!
" '&& " "
*+ "
" ')" $
' "
' "& " >
" "" )
)"
"
" ()
#66$
)"
#7
9 36 =& 8
/ 0
/ 0! "
& " * )=C" C* )= # ?C $ *+
$
' "
"
.
9 46 =& 8 234 5 16 "
8
"
"
#$1
)
$ *+ )
)" &
!
" '&& " "
*+ "
" ')" $
' "
)"
' "& " >
" "" )
)"
"
"
" ()
#66$
9 46 !"$
-7
)
)
8
* "
" *
9 6$?2 ))
.
)
)"
)"
7
"
')"
"
$
>
$
9
C
)
)"
&&
$ #$#$
+
! * "
8
* "
7
9
"
"
9 6$:6/160
+
92-$6
/+
9 -3$?
/! )"' 0
'
"
" 7
0
"
"
)"'
'
'
" 7
9
"
!! )"
9 6$32/320/6$?20
'
"
)"
)
"
"
@
9
"
9
9
! + "
9
"
)"
!
9
'*
94$1# ; $8
9 6$?
+
! * "
9#4$-
)
"
/+
9 #3$6
"
0
/! )"' 0
A
9
9 #$43 ; $
! + "
9
9
9 6$??
$
!
'*
9%$4:
$
)"
)"
(
9 6$:-2
$8
+
9%$%#
$
9 #$#? ; $8
(
9%$4?
$8
+
K
%
K
4
K
#
J
* )= D " D * )=0
* )= D " D * )=0
4 C# ,# , 8
4 C4 ,4, 8
9 4$14 ; $8
(
9 6$331
$8
+
9 6$:-?
$
9#$#? ; $8
9%$6:
$8
+
9%$2:
96$:-6
$8
+
96$:%3
(
$
A
/
/
)"
&&
$
/
/
)
$ #$#$
9 6$:6/#10
+
9
4 C-,#, 8
4 C#,4 , 88
9 44 !"$
9 4$-# ; $
' " *
' " *
"
A
'
'
.
$
9
C
9 6$32/2?0/6$?20
'
!"
>
/ 0!
* )=C" C* )= # ?C
' "
9 %$4 B %$1 9%$4/-?0 B %$1/#60 9 %61 =&
9 %$-/-?0 9 13 =&
9
"
')"
"
$
;'
;'
9 #6 =& 8 #18
" *
9 6$?2 ))
.
)
)"
)"
9 %$4 B %$1 9%$4/360 B %$1/460 9 %%1 =&
' 9 %$-/360 9 :? =&
9 -? =& 8
/ 0
& "
* )= D " D * )=0
* )= D " D * )=0
4 C#,4, 8
C 4 C#,4 , 8
94$1# ; $8
9#$-3 ; $8
(
$
* )=C" C* )=
/
* )= D " D * )=0
C 4 C-,#, 8
9 #$#? ; $8
* )= D " D * )=
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$1
)" &
!
" '&& " "
/ 0
/ 0! " )
*+ "
" ')" $
' "
& "
* )=C" C* )= # ?C $ *+ )
)"
' "& " >
" "" )
)"
.
$
' "
"
"
" ()
#66$
#$1
)" &
!
" '&& " "
/ 0
/ 0! " )
*+ "
" ')" $
' "
& "
* ) )C" C* = # ?C $ *+ )
)"
' "& " >
" "" )
)"
.
$
' "
)
"
"
" ()
#66$
9 46 !"$
17
)
" *
')" >
9 $
)
)"
+
8 9 6$?2 ))
"
C
$ #$#$
&&
! * " * "
.
)
)"
$
)"
7
B %$1 9%$4/260 B %$1/#60 9 %6? =&
' 9 %$4
' 9 %$-/260 9 36 =&
"
" 7 " 9 " + 9 6$:6/260 9-2$6
/+
0
9 " ' 9 6$32/120/6$?20
9 -%$- /! )"' 0
"
)"'
!! )"
" )"
) "
"
A
;'
9
9
9 4$1% ; $
)
+
8
! * " * "
27
9 26 =& 8
9 #6 =& 8
+
9 26 = 8
"
! + "
' " *
4 C4 ,4, 8
/
9
9 6$?6
'*
)"
9 4$14 ; $8
9 6$331
* )= D " D * )=0
4 C#,4 , 8
/
!
9
94$1# ; $8
J
(
(
7
$8
+
+
$
)
C
)"
$ #$#$
&&
$
9 %$4 B %$1 9%$4/?60 B %$1/#60 9 %-- =&
9 %$-/?60 9 %%4 =&
" 7 " 9 " + 9 6$:6/#10 9#4$/+
0
"
"
9
"
!"
9 6$32/2?0/6$?20
'
)"
)
"
9
! + "
' " *
$
$
9
9 46 !"$
"
9
9
9 #3$6
/! )"' 0
A
9 -$-- ; $
9
9 6$?6
$
A
" $5$
9%$%#
"
'
;'
9 6$:-?
8
'
'
$8
9#6:L#66
9 6$:-2
$
9 #6 =& 8 #1 "
" *
')" >
9 6$?2 ))
"
.
)
)"
)"
@
'
9 ?6 =& 8
K
%
* )= D " D * )=0
4 C#,4 , 8
9 4$1# ; $8 ( 9 6$32# $8 + 9%$-2 $
/
"
* )= D " D * )=0
J 9#6:L#66
" $5$
C 4 C#,4 , 8
9 4$1# ; $8
* )= D " D * )=
A
!
'*
)"
4 C-,-, 88
9 -$?6 ; $8 ( 9%$4- $8
/
* )= D " D * )=0
4 C-,# , 8
9 -$-: ; $8 ( 9%$41 $8
/
* )= D " D * )=0
C 4 C-,# , 8
9 -$-: ; $8
+
9%$?6
$
+
9%$22
$
J
K
* )=C" C* )=
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
%
"
#$1
)
$ *+ )
)" &
!
" '&& " "
*+ "
" ')" $
' "
)"
' "& " >
" "" )
)"
"
"
" ()
#66$
37
)
+
&&
9 ?6 =& 8
" *
')" >
8 9 6$?2 ))
! * " * "
.
)"
7
'
'
"
"
9
"
"
!! )"
4 C-,-, 8
4 C-,# 8
"
'
9 6$32/120/6$?0
"
+
)"
)
! + "
" *
"
9
!
91$26 ; $8
(
"
$
9-2$6
/+
9 #:$6
/! )"' 0
* 8" ' >
9 6$?2 ))
8" ' >" =
)" 0$
)"
7
0
"
$8
$8
+
+
9%$?#
;'
$
9%$##
$
J
$
K
%
(
9%$:-
$8
+
9%$#:
$
K
4
* )= D " D * )=0
9 1$26 ; $8
* )=C" C* )=
!"
0 "
"
#66$
'
9 %$-/%20 9 4% =&
9
9
"
"
C 2,# , 8
94$21
9%C
C -,# , 8
94$13
9%C
C
8
" ')" 0 " '&& "
""
* "
" *
") " $
' "
9 %2 !"8
"
" && +$
$ #$#$ / "
C
)"
"
"! &
B %$1 9 %$4/%20 B %$1/-60 9 ?4 =&
"
9 6$:6/#10
+
9 6$32/2?0/6$?20
'
9
"
9
'
! + "
' " *
"
C "
9%$4
;'
9 %$%4
*+ "
'
" 7
"
* )= D " D * )=0
C 4 C-,# 8
'&"'
)"
9%$44
/! " )
/ 0$
/ $ $> * )=
"
" ()
%7
9 %2 =& 8
9 -6 =& 8 #1 "
# -C $
* " $
9 4? !"$
A
9
9%$42
9 1$?- ; $8
'
9 1$%? ; $
'*
(
$
)"
/ 0
)
)"
$ #$#$
"
9
93$26 ; $8
4 C1,# , 8
/
= 8
C
9 6$:6/260
9
'
9
)"
#$3
"
'
"
$
9
"
)
9
;'
'
+
/ 0!
* )=C" C* )= # ?C
' "
9 %$4 B %$1 9%$4/?60 B %$1/%660 9 421 =&
9 %$-/?60 9 %%4 =&
" 7
)"'
/
9 %66 =& 8
/ 0
& "
.
$
9
9
M
9
!
9 #4$-
/+
0
9 #3$6
/! )"' 0
9 4$2# ; $
9 4$44 ; $
9
9 6$16
$
)"
94$21 ; $8 M 96$311
J
C6$?32/2 %10 9 4$4: ; $
9%C/ "
D+0 9%C /#C%$2:0 / " %60 9 6$?1
9 4$13 ; $8 M 9 6$343
J
C6$?32/# ?0 9 4$#- ; $
9%C/ "
D+0 9%C /4$2C%$4%0 / " %60 9 6$?3
C 2,# , 8
94$21 ; $8
)
)"
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
+
#$3
"
'
$
)"
/ 0
'
/! " )
/ 0$
/ $ $> * )=
"
" ()
'&"'
"
47
"
!"
0 "
"
#66$
9 %2 =& 8
9 -6 =& 8
"
9 %2 !"8 # -C $
* 8" ' >
9 6$?2 ))
8" ' >" =
)" 0$
)"
*+ "
7
'
" 7
"
C -
26 "
" && +$
$ #$#$ / "
C
9
"
"
"
9 6$:6/260
+
9 -2$6
9 6$32/120/6$?0
'
$
)"
/ 0
'
8
)"
"
"! &
/+
9 #:$6
9
9
7
;'
9
'
! + "
' " *
"
C -,# , 8
94$42
9%C
C 2,#, 8
94$-6
9%C
C -,-, 8
C
"
94$42 ;
C6$?32/2 %10
9%C/ "
9 4$-6 ;
C6$?32/2 %10
9%C/ "
9 4$-6 ;
C -,# , 8
9
M
9
!
9 6$?32"
"
9 %$:? ; $
9
94$42 ; $8
;'
)"
)
)"
0 "
"
#66$
34 5
" ')" 0 " '&& "
""
* "
" *
") " $
' "
16 "
8
* " $
9
"
C "
" && +$
$ #$#$ / "
C
)"
"
"! &
9 %$4 B %$1 9 %$4/%20 B %$1/-60 9 ?4 =&
9 %$-/%20 9 4 N=&
" 7
9
"
"
'
"
9 6$:6/160
+
9 6$32/320/6$?20
9
')" 9 /
$
$8 M 9 6$3#6
J
9 %$:? ; $
D+0 9%C /4$2C%$%?0 / " %60 9 6$?3
$8 M 9 6$12?
J
9 4$%# ; $
D+0 9%C /#C%$1?0 / " %60 9 6$?3
$8 M 9 6$3:%
J
!"
9 -6 =& 8
;'
A
9 6$16
9 42 !"8 3 ?C $
'
/! )"' 0
9 %$?4 ; $
B 6$%420" !
"
"
'
"
')" 9 /
=& 8
* 8" ' >
9 6$?2 ))
8" ' >" =
)" 0$
)"
0
9
*+ "
+
"
;'
/! " )
/ 0$
/ $ $> * )=
"
" ()
'&"'
#7
9 %$4 B %$1 9 %$4/%20 B %$1/-60 9 ?4 =&
' 9 %$-/%20 9 4% =&
9
#$3
"
'
"
34 5
* " $
"
" ')" 0 " '&& "
""
* "
" *
") " $
' "
9
"
9
'
! + "
' " *
9
M
9
!
/+
9 -3$?
0
/! )"' 0
9 %$24 ; $
B 6$%420" !
"
92-$6
9 %$6"
"
9 %$34 ; $
9
A
9 %$6
$
)"
C 2,2, 8
9#$6# ; $8 M 96$::9#$6# C%$6/2 %10 9 4$34 ; $
9%C
9%C/ "
D+0 9%C /# C%$#30 /
A
" %60 9 6$?-
A
C
C 2,2, 8
9#$6# ; $
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
+
#$?
1 =&
)"
"
9 - =& 8
"
)"
7
"
'
" 7
"
>
*
)"
&'"
"
C C
$D
*
"
9 6$32
"
;' "
!
"
9
#$:
- =&
*
*
*
*
234 5
! )"
!
;$
"
"
"
'
&
) 0/
*
"
#1 "
26 "
' " "
;'
!"
" 7
$
*
*
+ !
&'"
"
"
! )
!4 =&
8
*+
9 6$32
"
"
*
*
)"
)
"
+
! "
'
;' "
4C2>
;'
;'
' "
9 - =& 8 #1 "
"
"
*
"
" )
$
D #$1 / *
#$40
)"
7
B %$1 9 %$4/40 B %$1/-0 9 ?$? =&
' 9 %$4
9 %$-/40 9 4$? =&
"
3C%?0$
/%6 "
"
$
#$40
/6$32 '0
"
)"
9 4 =& 8
D #$1 / *
96$#: ;
"
*
'
*
9
"
D
!- =&
8
*+
9 6$32
"
/
! )
26 "
! "
' "
* 4C2>
"
;'
;'
"
9 %$4 B %$1 9 %$4/-0 B %$1/10 9 %-$- =&
9 %$-/-0 9 2$1 =&
"
12 = !
"
"
" ) +
26 " $
9 1 =& 8 234 5
"
'
)
"
"
234 5
$
*
!
'
/6$32 '0
#1 "
" "
2? = !
"
"
*
*
"
"
"
;'
!"
$D
$
3C%?0$
/%% "
>
*
' "
9 6$--4 ; $0
C C
"
96$43 ;
"
*
D
'
*
9
"
/
9 6$32
"
"
! )"
!
;$
9
"
*
&
) 0/
*
9 6$#63 ; $0
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
*
+ !
#$%6
"
"
'&& " " &'
!
' " *'
!.
&
&
.
)) & + ! ' $
& )
" %# &
* ".
!
>. )
& ) #6 !" & "$
'
!
&' .
: & ! ! ! ' !) $
"
"
#1 " $
.
"
)
46> #6> -6 & ! ! M " & O )" > . )
&& & " ! +
) $
"
"
*
'
#$%% "
"
%2(##$: ! "
'
"
I & "
7
&
"
) * "
9 %$4 B %$1
)"
7
. "
"+ 9
&
; !" !
!9
< 9.) /
09
)"
! )
!
)
9.' /
< "
' 9
"
"
>" =
" !
*
9
"
9
9 6$?2 ))
$ #$#> & /*0$
"
(
<
46
%6$?
4?$42
#:$62
#6
%6$?
-4$#?
2#$%?
"
-6 & !
%6$?
21$2%
13$#% & !
" 7
9 6$:6/#10:$:1 9#4# =& /+
9
C9 :$:1 C -/ * B% ?0".
9 :$:1C-/6$?3206$-6 9 ?$21 ; $
9 " ' 9 6$32/2?0/6$?30?$21 9 #4- =&
)=
"
" 7
9
"
"
0 9 /4- 6$??#60#6 9 ?%2$2 ; !"
+
9 :". 9 :/6$-60 9 #$16 ; $
"
9 /: C# 0". 9G:C#/6$?320H6$-6 9 4$22 ; $
&
?$2: =&
'
9 /%2C2 0". 9 G%2C2/6$?320H6$-6 9 -$42 ; $
)=7
" 9 2?/4$220 9 %-? =& H ! G6$1
' >
6$%2#
*
*
9#4$1
6$46?
9 6$1
*
6$41#
; $
3C%?> &$ 3C?#0
% 4
2 ?
2?
6$%:1
6$#63
6$#63
$
"
! )"' Q"
B
'
+
"
+
)
9 6C1/2?0-$42 9 %-? =& H
'
"
A
9 6$1/2?0-$42 B #1/#$160 9 43? =&
9 6$32/43?0 9 46? =&
B %$1
9 %$4
'
9 %$4/6$4 0 B %$1/6$? 0 9 46? =&
. *
9
A
'
"
9 46? =&
9 43$- =& 8
9 %#3 =& 8
; $
/! )"' 0
9 4/3$20". 9 4/3$206$-6 9 1$66 ; $
G
9 6$32/6$320/2?0
0
"
42$? =&
C #$1
'
7 /!
*
*
* "
"I
&
'
9 " /6$32 ' 0
;'
)"'
'&& " )
!
"
4?60H/ & )
;'
"
"
"
!
) &
"&
"
!$
4?60/
!
09
%2$6
46$" %# & " >
'
) )
I' #$
-$: ?
1$3:
"
&
0!
#1
%2(##$:
"
" +> ) &'"
9 %C
9 % C6$3?3 1 9 6$?3P 6$:6
&
C #$#$
7
9 G4- /)
'
)
> ?6F
& + !' $
9 :$:1 ; $
) "
C
'&& "
"
( '
.* "
/46F
%4C $ ' " & "
"
))
C! # -C $
* " $
". 96C-6 $
&
I'
"
"
)
>
9 %6: =&
9 %#3 =& A
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$%4 "
"
( '
.* "
%6(42 ! "
" 2?C $ ' " & "
'
! #-C $
* "$
)'
'&"' /* )=
0 "
I & "
7
/46F
))
.
"
" $
& +
"
> ?6F
!' $
" !"
0!
#1 "
)
9 3$#2 ; $
I & "
&
"
>
9 6$?2
C
"
+> )
> ?2F
#1 "
" & " *+ "
9 3$44 ; $
7
"
>
.* "
/%2F
"
' "& "
.$
!) "
"" " "
'
"
& $
5'
"I "
* "
9 6$?2
&
$ #$#> &
C
0
#-C $
! "
/*0$
&
$ #$#> &
"
&
* "
"
( '
1(-(#? "" )
$
" '"
) "
%6(42
". 96$241 $
) "
#$%# "
& !
* "
"
$
!
/*0$
"
&'"
9 %C
9 % C6$1%3 : 9 6$:# L 6$:6
&
D #$#$
" +> ) &'"
9 %C
9 %C6$:-% %6 9 6$:% L 6$:6
&
D #$#$
(
(
&'"
7 " 9 4/6$#320 9 6$32 $
"
%C% /".
)"
'"07
D4
9
9 3$44 C 4/6$32 B 6$%4206$32 9 2$:% ; $
"
" 7
9 6$:6/#103$#2 9 4#? =& /+
0
9
C#
9 :$:1 C #/ * B% ?0".
9 :$:1C#/6$?3206$241 9 2$:3 ; $
9 " ' 9 6$32/2?0/6$:602$:3 9 4#- =& /! )"' 0
"
)=
"
" 7
. * "
"
'
"& "
$
" 9 1". 9 1/6$2410 9 #$%1 ;
$
" 9 /1C4 0". 9G1C4/6$?320H6$241 9 4$4- ;
9 4/%6$20". 9 4/%6$206$241 9 %%$62 ; $
9 /4%C3 0". 9 G4%C3/6$?320H6$241 9 3$?4 ; $
)=7
G ' " 9 2?/4$4-0 9 %#6 =& H ! G6$1 ' 9 6C1/2?03$?4 9 434 =& H
' >
! )"' Q"
+
) "
A
9 6$1 '
B + " 9 6$1/2?03$?4 B #1/#$%10 9 #?1 =&
9 6$32/#?10 9 4?: =& 8 ' >
* ! )"' ) "
A
"
B %$1 9 " 9 4#- =&
' 9 %$4
' 9 %$4/6$4 0 B %$1/6$? 0 9 4#- =&
9 %2- =& 8
9 #% =& 8
9 %4# =&
. *
)
9 %2- =& A
>
"
9
"
+
"
"
)"
4C4 /#
9
C#
"
B/
4
07
- 0"
9 3$44C#/6$32 B 6$%4206$32C G44 -/4$20H6$32 9 2$22 ; $
"
" 7
0
9 " + 9 6$:6/#103$44 94#- =& /+
9 " ' 9 6$32/2?0/6$:602$22 9 4%3 =& /! )"' 0
)=
"
" 7 )'
& " $
"
9 %$42 ". 9%$42/6$320 9 6$:- ; $
"
9 /#$%2C% 0". 9 G#$32C%/6$?320H6$32 9 4$%1 ; $
9 G:$2 B"# $ # % H ". 9 G:$2 B #$46H6$32 9 :$2# ; $
9
> C#$2 ". 9:$2#C#$2/6$?3206$32 9 3$4# ; $
)=7 G ' " 9 2?/4$%10 9 %42 =& HP G6$1 ' 9 6$1/2?03$4# 9 424 =& H
+
) "
A
' >
! )"' Q"
9 6$1 ' + B + 9 6$1/2?03$4# B #1/6$:-0 9 4?2 =&
) "
A
9 6$32/4?20 9 4%- =& 8 ' > * )=
"
0 9 4%- =&
' 9 %$4/6$%2R B %$1/6$?24S
9 4% =& 8
9 %#: =& 8
9 %%? =&
>
. *
)
9 %#: =& A
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$%&
!
* "
"
I & "
"
"
( '
.* "
?(1(#- "" )
"
' "& "
$
! ) "
""
$
"
'" "
7
"
>
+> )
"I "
2 %1C $ & "
(
/*0$
&'"
9
C#
"
4
B/
$
"
07
"
- 0"
9 1$42C#/6$?32 B6$%4206$142B4G
"
"
" 7
9 " + 9 6$:6/#10%:$: 9 1-2 =& /+
0
9 " ' 9 6$32/2?0/6$?-0%2$: 9 2?% =& /! )"' 0
)=
"
" 7 )'
& " $
$
" 9 4$6". 94$6/%$260 9 #$66 ;
"
"
' >
9 6$1
"
'
92?/1$660 9 #-? =& HPG6$1
! )"' Q"
'
B
+
"
+
)
'
"
!
' > * )=
9 %$4/6$%236 B %$1/6$?23C0 9 -2: =&
. *
9 -2 =& 8
)
' >
A
>
9 42# =&
9 4:? =& A
)
"
-/40H6$142
9 %$#- $
" '
C%C4C $
"
= . > *'" "
!' )"
! $
$
" 9 -$6" 9 -$6/6$1420 9 4$26 ;
$
" 9
" D% " 9 4$26 C%$6/6$1420 9 %$?? ;
9 4/4 B%$20" 9 4/4 B%$206$142 9 4$2 B %$??
9
C# ". 94$2 B %$??C#/%$6606$142 9 4$2
)=7 G ' " 9 2?/%$??0 9 %-2 =& HPG6$1 ' 9 6$1/2?04$2 9%%# =& H
96$1/2?0%-$2 9 262 =& H
9 6$1/2?0%-$2 B #1/#$660 9 1%# =&
9 6$32/1%#0 9 -2: =& 8
9 4:? =& 8
+
A
&'" * )=
9 G:$2 B"# $ & H ". 9 G:$2 B #$1%H%$26 9 %:$3 ; $
9
C#$2 ". 9%:$3C#$2/%$660%$26 9 %-$2 ; $
'
4
0
/! )"' 0
9G46# /6$3202?9-$11 ; $
9 /2$66C% 0". 9G2$66C /%$660H%$26 9 1$66 ;
)=7 G
$
"
" 7
9 " + 9 6$:6/#101$42 946# =& /+
9 " ' 9 6$32/2?0/%$602$66 9 4%? =&
)"
%C% /#
"
07
9 C#
B ' ( 4 - 0"
9 %:$:6C#/6$?32 B 6$%420%$26 B G44 -/#0H $26 9 %2$: ; $
"
P 6$?2 $
)"
%C% /".
'"07
9
C4
9 1$42C4/6$?32 B
6$%4206$142
9 2$66 ; $
(
D #$#$
&'"
"
7 " 9 4/6$320 9 %$26
)"
%C% /".
'"07
9
C4
9 %:$:6C4/6$?32 B 6$%420%$26
9 %1$:6 ; $
C -8
9 6$?2/1$420 9 2$#% ; $
&'"
"
7
" 9 4/6$#%420 9 6$142
&
4C4 /#
*+
&
9 %C%$21 %6 9 6$?-P 6$:6
)"
)) & + ! ' 7/ 0 "
"
( '
0*
"
#-1 " & "
' * & )! " &
"
( ' ) & )"+
"
% 9 4 9 T
9 4/%606$#%42 9 1$42 ; $8
$ #$#> &
"
9 %C
#$%2$ 5
" &)
. "
) & )"+ /42F
> 32F
. > /*0 < " ' !
) &'"
& / 0> !" !
* "
9 6$?2
C
"
5'
9 %:$:6 ; $
) "
&
/%2F
> ?2F
0!
.$
#1 "
3?C $
" "
' " & " *+ " ! "
& $
"
A
"
+
C"
! )"'
)
"
A
9
G6$1 +
B ' "H 9 6$32G6$1/#10/4$2 B %$??0 B 2?/%$??0H
"
9 6$32G2- B%-:$1H 9 46# =&
!
9 4$4- $
)= "
" .
9 4$42 $
9 " G6$1 +
B + "H 9 6$32G6$1/2?04$2 B#1/4$2 0H
9 6$32G?3/4$420 B :6H 9 4%- =&
*
"
" >
"
9 46# =& 8
9 4$42 $
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
#$%1$
2(#C 4( 4
>
.
"
)) & + ! ' >
36 =&
'
"
" "
" !)
)" '
* " " 2C $ $ < " "
' )) &" * "
>"
")
'"& 0> '
234 5
26 " T
)"
'&"' "
"$
" ) + 46 =&
".
!
& )! /%4C $
9 -$66 ; $
) "
"
C
"
* " &
$ #$#> &
"
+> )
&
>
9 6$?2
#$%3$
. " "
" 2 >
)"
) "
/*0$
&
&'"
"
'"7
9 -$66C%/6$32 B 6$%4206$26 9 #$21 ; $
7
'
'
"
"
( '
9 " +
9 " '
)"
"
9
C4
"
" 7
9 6$:6/260-$66 9 %?6 =& /+
0
9 " '
9 6$32/120/6$?20#$21 9 %-? =&
" ' ".
7
B / 4 - 0"
9 #$%# B6$63%- 4 9 #$4? ; $
9%$-?8 + 9 %$2 $
)+ ! )"
)= "
!
9 %C
'
G4$13/6$320H 9
!4$13
4
"
$
4
B%$32
9 6$:3 $
"
" >
"
9 %#1 =& 8
."
)
&'"
9 %$2 $
'"7
9 -$66C%/6$?32 B 6$%4206$26 9 #$26 ; $
C%
)"
7
'
'
/! )"' 0
"
( '
9
"
9
)"
5
"
"
" 7
9 6$:6/#10-$66 9 %#6 =&
+
"
9%$4 B %$1 9 %$4/460 B %$1/160 9 %46 =&
9 %$-/460 9 4? =&
9
'
"
"
'
"
/+
0
96$32/2?0/6$?20#$26 9 %4: =&
'
".
/! )"' 0
7
9# B 4 C" 9# B 4 C6$2 9 -$2 $
9 C4
B / 4 0"
9 -$66 C 4/6$?32B 6$%4206$26 B G 4 -/-$20H6$26
9 #$66 B 6$643? 4
;'
9 C6$:61 G-/%$20H 9 6$?2
& )
4
*
+>
/*0$
D #$#$
)"
9
9 %$4 B %$1 9 %$4/460 B 1/360 9 %#1 =&
9 %$-/460 9 4? =&
9 -$66C4/6$32 B6$%4206$26B G 4 -/%$320 6$26
9 #$%# B6$63%- 4
;'
"
9%#1 G6$32/6$?2012H 9 #$4? ; $
)= !!)
$ #$#> &
"
'
&
9 %C
9 %C6$:61 9 %$2> 9 6$?2
9 6$?2
)"
& + ! ' > " ) + 46 =&
! 3?C $
* "
)
>
"
" * " !
*+ * "
" * )
& $
#1 " $
* "
9 6$?2
&
9 %C6$:61 -2
."
C%
"
>
C
9 %C
)"
9
))
!
9 -$66 ; $
&
D #$#$
9%$2>
2(#C 4( 4
>
. "
16 =&
$
' "
> " )) & " T
. "
" #C%4 $
'&"'
"
" $
"
9 #$66 B6$643?
9%46 G6$32/6$?202?H 9 #$42 ; $
4
9#$42 ; $
9 #$66 $
)= !!) )+ ! )"
9 %C
9 C6$:61 G-/#0H 9 6$:4 L 6$:6 (
)= "
!
'
& )
!4$13
" $
G4$13/6$?320H4 9 4B-$24
9
*
"
" >
9 %46 =& 8
9# $
"
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
"
I "
#$%?$
&'" "
'
' ! " ") ' * '
"
! ' > ') " " "
( ' ! )"
"
! ) ' +* )
'
" " ! ' & ""
" ' "
&
.
"
)
"
!
'&"'
"
" $
#1 "
. " %C $
/
$
I *
.
'
$ )'
* " $
"
""
" + C #$#> &
"
"
+> )
9 1$-
* " &
>
9 6$?2
&
/*0$
&'"
"
9 /3 C
"
9
"
C #$#
5'
9 %C
9 C6$:1#
)=7G
"& "
"
( '
"
"
+
"
9
"
'
)"
5
'
"
9
9
"
! )"'
B
'
C"
+
"
+
"
" >
)
9 6$1/2?0:$3% 9 ##? =& H
'
"
A
9 6$1/2?0:$3% B #1/6$:-0 9 #34 =&
"
'&"'
9 4%6 =& 8
"
'
"
)
9 4$#1
$
"
9 4$2
C4
$8
B/
4
;'
'
".
9#
$8
4
"
;
/! )"' 0
7
' > &$ %6C%6$
9 4$2 $>
- 0"
4
-/#$60H6$142 9 2$63B6$624%
4
9 4%6 G6$32/6$?202?H 9 2$1? ; $
9 2$63 B 6$624%
9 %C
0
9 6$32/2?0/6$?202$3? 9 4%- =&
'
9 1$-?C 4/%$66 B 6$%4206$142 B G
)=
9 2?/6$2:0 9 #- =& H P G6$1
" 7
9 6$:6/#101$-? 9 4%6 =& /+
"
%
0" 9 /3C#C4$206$142 9 6$:- ; $
'"7
9 1$-?C%/%$66 B 6$%4206$142 9 2$3? ; $
C%
9
%
9 6$32/#340 9 43: =& 8
*
"
D
& " $
C#$2 " 9 %4$%3C#$2/%$%4206$142 9 :$3% ; $
9
9 6$1
."
4
" 7 )'
C6$2 " 9 6$:-C6$2/%$66 B 6$%4206$142 9 6$2: ; $
' >
)"
9
"
9 G $2 B 1 B"( $ & H" 9 G $2 B 1/4$#10 B "# &) $ & H6$142 9 %4$%3 ;
&
9 6$?2
$>
4 !4
)= '&"'
9 1$-? ; $
) "
#$%?> &
4
9 2$1? ; $8
9 #$-4
9 C6$:1# GL-/#$-40H 9L6$:6
$
(8 '
94%6 G6$32/2?06$:6H 9 2$#1 ; $8
6$:6
(
9 4$#1
$
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
"
A
#$%:$
'
" " ! "
I *$ #$%?> ) &'" "
'
.
"
') "
"
" *
>
'
#$32 $
9 1$-? ;
(
#$%:> &
)"
"
""
#$#> &
" &
/*0$
>
9 6$?2
9 6$:6 ))
9 4%6 =& /I *$ #$%?08
"
I *
$
) "
" +C
!I *$ #$%?
;'
" )
;'
" ""
&
" -C $
. "
( ' &
*
' $ !I *$ #$%?
"
#1 "
. " %C $
* " $
&
'
" I *$ #$%?$
'
9 4$#1
$8
-C# . " %66F
9 4$#1
!
$/
)"
'
B' (
D#
9
9 2$#1 ; $
4 !4
4
7
) "
!
- 0"
9 1$-?C#/%$66 B 6$%4206$142 B G
4
4
9 -$#3 B G4$#1 -/#0 B
2$#1 9 -$11 B
4
4$#1
$
I *$ #$%?0
4?8
4
4
-/#0 B
-/-$#320H6$142
-/-$#320H6$142 9 -$11 B
4
4?
9 -$-# >
;'
-$-#
$
! !'
"
"
!
$
!
$
& )" ) "+>
9 4$2
! 9 #$32
9
$
9
$
C#
B' (
4
9 -$#3 B G#$32
)"
* "
"
/"
'
)"
9
'
"
&
&
"
. " %66F
"
)"
)
9
&'"
'
)"
4C4 . " 1 ? ! "
0$ !
> ! '
"
!
+
$
!
!'
2$#1 9 2$%6 B
4
9 #$32
$
4
"
"
"
>
- 0"
$%420 $142 B G
-/#0 B
4?8
-/#0 B
4
-/-$#320H6$142
4
%-/-$#320H6$142 9 2$%6 B
;'
9
4
4$36
4
4?
9 4$36 $
$
! !'
"
"
!
4C4 . " 1 ? !
)" 7
C4
9 1$-? C 4/%$66 B 6$%4206$142 9 2$63 ; $
1 ? ! ;'
5
)
$
!I *$ #$%? .
9 1$-?C#/ $66 B
'
-$2
9 /1 ?02$#1 9 -$64 ;
#C# . " 3 ? !
/
"
0 9 4$2
)" 7
$8 / '
)
$/
")
"
0
0 9 4$2 B 4$2C6$142 9 -$#32
$
B' (4 - 0"
C#
9 1$-? C #/%$66 B6$%4206$142 B G
9 -$#3 B
4
4
4
-/#0 B
-/-$#320H6$142
%%$#:
3 ? ! ;'
9 /3 ?02$#1 9 -$1: ;
-$1: 9 -$#3 B
4
%%$#:8
;'
$
9 %$:%
$
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
$
#$46$
D )'" 234 5
+ * " ) + 4- =&
26 " & " $ / ! "
9 4- =& 8
9 31 =& 8 234 5
@
)"
96$:
"
+
)"'
9 6$:
'
)"
26 "
>
/260 9 -2
"
)"
9 6$32
7
>'
!
8
7
!! )"
96$32
"
31 =&
D $ 10
7
/120 9 -?$32
9 %$4
'
A
B %$1 9 %$4/4-0 B %$1/310 9 %26$- =&
9 %$-/4-0 9 ##$1 =&
'
@
)"
;'
"
9
)"
"
"
*
*
)
"
*
"
9
A
9#$#- ;
*
"
D 1
"
"
!"
;'
' "
$
)
*
*
+ !"
&'"
/
D
3C%?0$
C# C
$D
/-$2 "
&
) 0/
*
9 #$:? ;
$0
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
7.6. A W24×94 beam on a 6-ft span (see acompanying figure) underpins a column
that brings 110 kips dead load and 280 kips live load to its top flange at a location 2.5 ft
from the left support. The column bearing plate is 12 in. measured along the beam, and
the bearing plates at the end supports are each 8 in. Investigate this beam of A992 steel for
(a) flexure, (b) shear, and (c) satisfactory transmission of the reactions and concentrated
load (i.e., local web yielding, web crippling, and sidesway web buckling). Specify changes
(if any) required to satisfy the AISC Specification.
Use LRFD Design Method
(a) Obtain factored loads:
Wu = 1.2(110) + 1.6(280) = 580 kips
Wu ab
580(2.5)(3.5)
Mu =
=
= 846 ft-kips
L
6
Wu b
580(3.5)
Vu =
=
= 338 kips
L
6
(b) Check flexural strength assuming adequate lateral support (AISC F2.1):
Flange and web local buckling slenderness limits, Fy = 50 ksi steel:
# "
"
#
#
"
bf
65
640
h
= 5.2 ≤ λp = p = 9.2 ;
= 41.9 ≤ λp = p = 90.5 OK
2tf
tw
Fy
Fy
φb Mn = φb Mp = φb Zx Fy
= 0.9(254)(50)/12 = 953 ft-kips
[φb Mn = 953 ft-kips] > [Mu = 846 ft-kips] OK
(c) Check shear strength (AISC G2.1):
q
h
For rolled I-shapes, when
= 41.9 ≤ 2.24 E/Fy = 53.9 , φv = 1.0 and
tw
Cv = 1.0.
φv Vn = φv (0.6Fy )Aw Cv = φv (0.6Fy )dtw Cv
= 1.0(0.6)(50)(24.31)(0.515)(1.0) = 376 kips
[φv Vn = 376 kips] > [Vu = 338 kips] OK
(d) Check local web yielding strength (AISC J10.2):
Rn = (5k + N )Fy tw Interior Reaction
Rn = (2.5k + N )Fy tw Exterior Reaction
Rn = (5k + N )Fy tw = [5(1.625) + N ] (50)(0.515)
Solving for Ru = 580 kips, N = 14.4 in. at the interior reaction.
Rn = (2.5k + N )Fy tw = [2.5(1.625) + N ] (50)(0.515)
Solving for N to give Ru = 338 kips, N = 9.1 in. at the left exterior reaction.
Solving for N to give Ru = 242 kips, N = 5.3 in. at the right exterior reaction.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Check web crippling strength (AISC J10.3):
For interior reactions:

!1.5  s
EFyw tf
3N tw

φRn = φ0.80t2w 1 +
d
tf
tw
"
1.5 # r
3N
0.515
(29000)(50)(0.875)
= (0.75)(0.80)(0.515)2 1 +
24.31 0.875
0.515
Solving for N to give Ru = 580 kips, N = 23.7 in.
For exterior reactions, assuming N/d > 0.2:

!1.5  s
EFyw tf
4N
tw

φRn = φ0.80t2w 1 +
− 0.2
d
tf
tw
"
1.5 # r
4N
0.515
(29000)(50)(0.875)
= (0.75)(0.40)(0.515)2 1 +
− 0.2
24.31
0.875
0.515
Solving for N to give Ru = 338 kips, N = 24.2 in. Check [N/d = 1.00] > 0.2.
Solving for N to give Ru = 242 kips, N = 13.8 in. Check [N/d = 0.57] > 0.2.
(f) Check sidesway web buckling strength (AISC J10.4):
When the compression flange is restrained against rotation, for (h/tw )/(Lb /bf ) = ∞ >
2.3, this limit state does not apply.
Conclusion:
In accordance with AISC-J10.7, “At unframed ends of beams and girders not otherwise
restrained against rotation about their longitudinal axes, a pair of transverse stiffeners,
extending the full depth of the web, shall be provided.” The 24.2 in. bearing plate required
at the left reaction, the 13.8 in. bearing plate required at the right reaction, and the 23.7 in.
bearing plate required at the load are all too long. Bearing stiffeners should be provided.
The beam has adequate flexural and shear strength.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
7.7. A W16×77 section of A992 steel is to serve on a 10-ft simply supported span.
The wall bearing length is 10 in. What maximum slowly moving concentrated service load
(25% dead load; 75% live load) may be carried?
Use LRFD Design Method
(a) Obtain factored loads:
Wu = 1.2(0.25W ) + 1.6(0.75W ) = 1.5W
Wu L
Wu (10)
Mu =
=
= 2.5Wu with load at midspan
4
4
Vu = 1.0Wu with load at support
(b) Check flexural strength assuming adequate lateral support (AISC F2.1):
Flange and web local buckling slenderness limits, Fy = 50 ksi steel:
# "
#
#
"
"
bf
65
h
640
= 6.8 ≤ λp = p = 9.2 ;
= 31.2 ≤ λp = p = 90.5 OK
2tf
tw
Fy
Fy
φb Mn = φb Mp = φb Zx Fy = 0.9(150)(50)/12 = 563 ft-kips
Mu = 2.5Wu = 563 ft-kips; Wu = 225 kips
(c) Check shear strength (AISC G2.1):
q
h
For rolled I-shapes, when
= 31.2 ≤ 2.24 E/Fy = 53.9 , φv = 1.0 and
tw
Cv = 1.0.
φv Vn = φv (0.6Fy )Aw Cv = φv (0.6Fy )dtw Cv
= 1.0(0.6)(50)(16.52)(0.455)(1.0) = 225 kips
Vu = 1.0Wu = 225 kips; Wu = 225 kips
(d) Check local web yielding strength (AISC J10.2):
Rn = (5k + N )Fy tw Interior Reaction
Rn = (2.5k + N )Fy tw Exterior Reaction
Exterior reaction controls because Wu is both the interior and exterior load
φRn = φ(2.5k + N )Fy tw
= 1.0 [5(1.4375) + N ] (50)(0.455) = 309 kips
φRn = 1.0Wu = 309 kips; Wu = 309 kips
(e) Check web crippling strength (AISC J10.3):
For exterior reactions, for [N/d = 10/16.52 = 0.61] > 0.2:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.

φRn = φ0.80t2w 1 +
4N
− 0.2
d
"
= (0.75)(0.40)(0.455)2 1 +
!1.5  s
EFyw tf
tw

tf
tw
4(10)
− 0.2
16.52
= 196 kips
φRn = 1.0Wu = 196 kips; Wu = 196 kips
#r
0.455 1.5
(29000)(50)(0.76)
0.76
0.455
(f) Check sidesway web buckling strength (AISC J10.4):
When the compression flange is restrained against rotation, for (h/tw )/(Lb /bf ) = ∞ >
2.3, this limit state does not apply.
Conclusion:
Web crippling controls!
Max Wu = 196 kips; Service Load W = Wu /1.5 = 131 kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
7.15. Select the lightest W8section of A992 steel to use as a purlin on a roof sloped
30◦ to the horizontal. The span is 21 ft, the load is uniform 0.18 kip/ft dead load plus
the purlin weight and 0.34 kip/ft snow load. Lateral stability is assured by attachment of
the roofing to the compression flange. Assume the load acts through the beam centroid,
there are no sag rods, and biaxial bending must be assumed. Any torsional effect can be
resisted by the roofing and therefore it can be neglected.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.18 + 0.035) + 1.6(0.34) = 0.80 kips/ft
wu L2
(0.80)(21)2
=
= 44.2 ft-kips
8
8
Mux = Mu cos θ = 44.2 cos 30◦ = 38.3 ft-kips
Muy = Mu sin θ = 44.2 sin 30◦ = 22.1 ft-kips
Mu =
(b) Use AISC H2 with no axial load term and the conservative estimate Mn = SFy :
Muy
Mux
+
≤1
φb Mnx φb Mny
Muy Sx
Mux
38.3(12) 22.1(12) Sx
Sx ≥
+
=
+
φb Fy φb Fy Sy
0.9(50)
0.9(50) Sy
Sx
≥ 10.2 + 5.9
Sy
For Sx on the order of 3 to 4: Sx ≈ 27.9 to 33.8 in.3
Assuming Zx ≈ 1.12Sx : Zx ≈ 31.2 to 37.8 in.3
Using AISC Table 3-2 Selection by Zx , for W8 beams, find W8×35 with Zx = 34.7 in.3
Check the strength.
Muy
Mux
38.3(12)
22.1(12)
+
+
=
φb Fy Sx φb Fy Sy
0.9(50)(31.2) 0.9(50)(10.6)
= 0.3272 + 0.5561
= 0.8833 ≤ 1 OK
Beam
Mnx
ft-kips
Mny
ft-kips
Check
W8×35
W8×31
117
103
39.8
34.8
0.3272 + 0.5561 = 0.8833
0.3690 + 0.6321 = 1.0011
OK
NG
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
8.21. Assume a single W section is to serve as a crane runway girder which carries a
vertical loading, as shown. In addition, design must include an axial compressive force of
14 kips and a horizontal force of 4 kips on each wheel applied 4 14 in. above the top of the
compression flange. Assume torsional simple support at the ends of the beam. Select the
lightest W14 section of A992 steel using the β modified flexure analogy approach. Note:
All loads except weight of the crane runway girder are live loads.
Use LRFD Design Method
(a) Obtain factored loads:
Use an estimated beam weight of 0.342 kips/ft and an estimated beam depth of 14 in.
Wux = 1.6(40) = 64 kips – Lifted load
Wuy = 1.6(4) = 6.4 kips – Lateral load
wux = 1.2(0.020 + 0.342) = 0.4344 kips/ft – Dead load
40 − 4/2
x=
= 19 ft – location for maximum moments
2
2(64)(19)2
2Wux x2
=
= 1155 ft-kips – Lifted load moment
Mux1 =
L
40
Mux2 = 0.25Mux1 = 0.25(1155) = 288.8 ft-kips – Impact moment
wux x(L − x)
(0.4344)(19)(40 − 19)
Mux3 =
=
= 86.7 ft-kips – Dead load moment
2
2
Mux = Mux1 + Mux2 + Mux3 = 1531 ft-kips
2Wuy x2
2(6.4)(19)2
=
= 115.5 ft-kips
L
40
Tu = Wuy (d/2 + rail height) = 6.4(14/2 + 4.25) = 72.00 in-kips
Muy =
(b) Use the β modified flexure analogy to find the equivalent lateral moment. Use β ≈ 0.5.
Tu
72.00
Vf =
≈
= 5.143 kips – flange force using h ≈ d
h
14
2Vf x2
(5.143)(19)2
Mf = β
= 0.5
= 46.41 kips – flange moment
L
40
My = 2Mf = 2(46.41) = 92.83 kips – equivalent lateral moment
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(c) Select a beam using AISC H1:
Muy + My Sx
1531(12) (115.5 + 92.83)(12) Sx
Mux
+
=
Sx ≥
+
φb Fy
φb Fy
Sy
0.9(50)
0.9(50)
Sy
Sx
≥ 408.2 + 55.56
Sy
For Sx on the order of 3 to 5: Sx ≈ 574.9 to 686.0 in.3
Assuming Zx ≈ 1.12Sx : Zx ≈ 643.8 to 768.3 in.3
Using AISC Table 3-2 Selection by Zx , for W14 beams, find W14×342 with
Zx = 672 in.3
(d) Check the beam more accurately using the properties from AISC Table 1-1.
s
r
GJ
(11154)(178)
λ=
=
= 0.02578
ECw
(29000)(103000)
λL = (0.02578)(40)(12) = 12.38
β = 0.16 for a point load at x and simply supported ends
Tu = Wuy (d/2 + rail height) = 6.4(17.5/2 + 4.25) = 83.20 in-kips
Tu
83.20
Vf =
=
= 5.536 kips
h
15.03
2Vf x2
(5.536)(19)2
= 0.16
= 16.19 ft-kips
Mf = β
L
40
My = 2Mf = 2(16.19) = 32.38 ft-kips
Mux Muy My
1531(12) 115.5(12) 32.38(12)
+
+
+
+
=
Sx
Sy
Sy
558
221
221
= 32.92 + 6.273 + 1.758
= 40.95 ksi ≤ φFy = 0.9(50) = 45 ksi OK
fun =
The beam is sufficient. Check for a lighter beam.
Section
Mux
ft-kips
β
My
ft-kips
fun
ksi
φFy = 45 ksi
W14×342
W14×311
1531
1523
0.16
0.17
32.38
34.35
32.92 + 6.273 + 1.758 = 40.95
36.12 + 6.966 + 2.072 = 45.16
OK
NG
Use W14×342, A992 steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.2, Case 1. Determine the maximum concentrated load P that can act at midspan on
a simply supported span of 20 ft. Lateral supports exist only at the ends of the span. The
service load is 65% live load and 35% dead load. The section is W21×62 of Fy = 50 ksi
steel.
Use LRFD Design Method
(a) Obtain factored loads:
Wu = 1.2(0.35W ) + 1.6(0.65W ) = 1.46W
wu = 1.2(62/1000) = 0.0744 kips/ft
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends only. The longest unbraced length is
Lb = 20 ft. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.5M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.5M
12.5M
Cb =
(1.0) = 1.32
2.5M + 3(0.5M ) + 4(1.0M ) + 3(0.5M )
(c) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 6.7 ≤ λp = 0.38
= 46.9 ≤ λp = 3.76
= 90.6 ;
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(144)/12 = 600 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-16, Lp = 6.25 ft and Lr = 18.1 ft.
[Lr = 18.1 ft] < [Lb = 20 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
Cb π 2 E
Jc
Lb
Mn = Fcr Sx = Sx
1
+
0.078
Sx ho rts
(Lb /rts )2
s
12(20) 2
(1.32)π 2(29000)
(1.83)(1)
= (127)
1 + 0.078
(127)(20.4)
2.15
(12(20)/2.15)2
= 415 ft-kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(415) = 374 ft-kips
(d) Calculate the maximum service load.
Wu L wu L2
+
4
8
(1.46W )(20) (0.0744)(20)2
374 =
+
= 7.30W + 3.72
4
8
W = 50.7 kips
φb Mn =
Maximum Service Load W = 50.7 kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.2, Case 2. Determine the maximum concentrated load P that can act at midspan on
a simply supported span of 24 ft. Lateral supports exist only at the ends of the span. The
service load is 65% live load and 35% dead load. The section is W24×84 of Fy = 50 ksi
steel.
Use LRFD Design Method
(a) Obtain factored loads:
Wu = 1.2(0.35W ) + 1.6(0.65W ) = 1.46W
wu = 1.2(84/1000) = 0.101 kips/ft
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends only. The longest unbraced length is
Lb = 24 ft. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.5M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.5M
12.5M
Cb =
(1.0) = 1.32
2.5M + 3(0.5M ) + 4(1.0M ) + 3(0.5M )
(c) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-16 and 1-17.
s
s
# "
# "
#
"
bf
h
E
E
= 5.86 ≤ λp = 0.38
= 45.9 ≤ λp = 3.76
= 90.6 ;
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(224)/12 = 933 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-16, Lp = 6.89 ft and Lr = 20.3 ft.
[Lr = 20.3 ft] < [Lb = 24 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
Cb π 2 E
Jc
Lb
Mn = Fcr Sx = Sx
1
+
0.078
Sx ho rts
(Lb /rts )2
s
12(24) 2
(1.32)π 2(29000)
(3.7)(1)
= (196)
1 + 0.078
(196)(23.3)
2.37
(12(24)/2.37)2
= 579 ft-kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(579) = 521 ft-kips
(d) Calculate the maximum service load.
Wu L wu L2
+
4
8
(1.46W )(24) (0.101)(24)2
521 =
+
= 8.76W + 7.26
4
8
W = 58.7 kips
φb Mn =
Maximum Service Load W = 58.7 kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.2, Case 3. Determine the maximum concentrated load P that can act at midspan on
a simply supported span of 30 ft. Lateral supports exist only at the ends of the span. The
service load is 65% live load and 35% dead load. The section is W30×99 of Fy = 50 ksi
steel.
Use LRFD Design Method
(a) Obtain factored loads:
Wu = 1.2(0.35W ) + 1.6(0.65W ) = 1.46W
wu = 1.2(99/1000) = 0.119 kips/ft
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends only. The longest unbraced length is
Lb = 30 ft. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.5M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.5M
12.5M
Cb =
(1.0) = 1.32
2.5M + 3(0.5M ) + 4(1.0M ) + 3(0.5M )
(c) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-14 and 1-15.
s
s
# "
# "
#
"
bf
h
E
E
= 7.8 ≤ λp = 0.38
= 51.9 ≤ λp = 3.76
= 90.6 ;
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(312)/12 = 1300 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-15, Lp = 7.42 ft and Lr = 21.4 ft.
[Lr = 21.4 ft] < [Lb = 30 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
Cb π 2 E
Jc
Lb
Mn = Fcr Sx = Sx
1
+
0.078
Sx ho rts
(Lb /rts )2
s
(1.32)π 2(29000)
(3.77)(1) 12(30) 2
= (269)
1 + 0.078
(269)(29)
2.62
(12(30)/2.62)2
= 585 ft-kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(585) = 527 ft-kips
(d) Calculate the maximum service load.
Wu L wu L2
+
4
8
(1.46W )(30) (0.119)(30)2
527 =
+
= 11.0W + 13.4
4
8
W = 46.9 kips
φb Mn =
Maximum Service Load W = 46.9 kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 1: dead load is 0.9 kips/ft, live load is 2 kips/ft, span is 20 ft, the beam has continuous
lateral support, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.9 + beam wt) + 1.6(2) ≈ 4.28 kips/ft
4.28(20)2
wu L2
=
= 214 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
Since the beam has continous lateral support, Cb = 1.0.
(c) Since the unbraced length is relatively short, select a beam using Table 3-2 Selection
by Zx , AISC Manual, pp. 3-11 to 3-19. Assume λ ≤ λp for a compact section.
Mu
(214)(12)
Required Zx =
= 57.1 in.3
=
φb Fy
(0.9)(50)
Select: W18×35, Zx = 66.5 in.3
(d) Correct the moment for the selected beam weight.
Mu = 214 +
1.2(beam wt)L2
1.2(35/1000)(20)2
= 214 +
= 216 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.5 ≤ λp = 3.76
= 90.6 ;
= 7.06 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(66.5)/12 = 277 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
The beam has continuous lateral support, so [Lb = 0] < Lp and lateral torsional
buckling does not apply, AISC-F2.1(a).
Yielding controls! Calculate the design moment strength.
φb Mn = (0.9)(277) = 249 ft-kips
The W18×35 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 35 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W18×35
W16×31
W14×34
Mu
φb Mn
ft-kips
ft-kips
216
216
216
249
203
205
bf
2tf
h
tw
OKAY?
7.06
6.28
7.41
53.5
51.6
43.1
OK
NG
NG
Use W18×35 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 2: dead load is 0.9 kips/ft, live load is 2 kips/ft, span is 20 ft, the beam has lateral
support at the ends and midspan, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.9 + beam wt) + 1.6(2) ≈ 4.28 kips/ft
4.28(20)2
wu L2
=
= 214 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of
the beam. Use the segment from 0 ft to 10 ft with Lb = 10 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is relatively short, select a beam using Table 3-2 Selection
by Zx , AISC Manual, pp. 3-11 to 3-19. Assume λ ≤ λp for a compact section.
Mu
(214)(12)
Required Zx =
=
= 57.1 in.3
φb Fy
(0.9)(50)
Select: W18×35, Zx = 66.5 in.3
(d) Correct the moment for the selected beam weight.
Mu = 214 +
1.2(beam wt)L2
1.2(35/1000)(20)2
= 214 +
= 216 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.5 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 7.06 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(66.5)/12 = 277 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-18, Lp = 4.31 ft and Lr = 12.4 ft.
Lp = 4.31 ft < [Lb = 10 ft] ≤ [Lr = 12.4 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(57.6)
10 − 4.31
= (1.30) 277 − 277 −
12
12.4 − 4.31
= 260 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(260) = 234 ft-kips
The W18×35 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 35 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
W18×35
216
234†
7.06
†
W16×31
216
186
6.28
W14×34
216
205
7.41
† Inelastic lateral torsional buckling controls
h
tw
OKAY?
53.5
51.6
43.1
OK
NG
NG
Use W18×35 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 3: dead load is 0.9 kips/ft, live load is 2 kips/ft, span is 20 ft, the beam has lateral
support at the ends only, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.9 + beam wt) + 1.6(2) ≈ 4.28 kips/ft
4.28(20)2
wu L2
=
= 214 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends only. The longest unbraced length is Lb =
20 ft. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.750M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.750M
12.5M
Cb =
(1.0) = 1.14
2.5M + 3(0.750M ) + 4(1.0M ) + 3(0.750M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 20 ft.
Mu
214
Required φb Mn =
=
= 188 ft-kips
Cb
1.14
Select: W14×48, φb Mn = 193 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 214 +
1.2(48/1000)(20)2
1.2(beam wt)L2
= 214 +
= 217 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 33.6 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 6.75 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(78.4)/12 = 327 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-17, Lp = 6.75 ft and Lr = 21.1 ft.
Lp = 6.75 ft < [Lb = 20 ft] ≤ [Lr = 21.1 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(70.2)
20 − 6.75
= (1.14) 327 − 327 −
12
21.1 − 6.75
= 243 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(243) = 219 ft-kips
The W14×48 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 48 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W14×48
217
219†
W21×48
217
200‡
W21×44
217
119‡
W18×46
217
134‡
W16×45
217
163‡
W16×31
216
62.6‡
W14×48
217
219†
W14×43
217
187†
W14×38
216
120‡
W12×45
217
188†
W10×45
217
177†
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
6.75
9.47∗
7.22
5.01
6.23
6.28
6.75
7.54
6.57
7
6.47
33.6
53.6
53.6
44.6
41.1
51.6
33.6
37.4
39.6
29.6
22.5
OK
NG
NG
NG
NG
NG
OK
NG
NG
NG
NG
‡
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked (see below)
For the limit state of compression flange local buckling, AISC–F3.2, for W21×48:
∗
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
9.47 − 9.15
0.7(50)(93)
= 446 − 446 −
12
24.1 − 9.15
= 442 ft-kips
Use W14×48 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 4: dead load is 0.7 kips/ft, live load is 1.4 kips/ft, span is 28 ft, the beam has lateral
support at the ends and midspan, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.7 + beam wt) + 1.6(1.4) ≈ 3.08 kips/ft
3.08(28)2
wu L2
=
= 302 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of
the beam. Use the segment from 0 ft to 14 ft with Lb = 14 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 14 ft.
Mu
302
Required φb Mn =
=
= 232 ft-kips
Cb
1.30
Select: W14×48, φb Mn = 239 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 302 +
1.2(48/1000)(28)2
1.2(beam wt)L2
= 302 +
= 307 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 33.6 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 6.75 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(78.4)/12 = 327 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-17, Lp = 6.75 ft and Lr = 21.1 ft.
Lp = 6.75 ft < [Lb = 14 ft] ≤ [Lr = 21.1 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(70.2)
14 − 6.75
= (1.30) 327 − 327 −
12
21.1 − 6.75
= 327 ft-kips
Yielding controls! Calculate the design moment strength.
φb Mn = (0.9)(327) = 294 ft-kips
The W14×48 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W14×48
307
294
W14×53
308
327
W21×48
307
366†
W21×44
307
244‡
W18×46
307
259‡
W16×45
307
283†
W14×48
307
294
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
6.75
6.11
9.47∗
7.22
5.01
6.23
6.75
33.6
30.9
53.6
53.6
44.6
41.1
33.6
NG
OK
OK
NG
NG
NG
NG
‡
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked (see below)
For the limit state of compression flange local buckling, AISC–F3.2, for W21×48:
∗
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
9.47 − 9.15
0.7(50)(93)
= 446 − 446 −
12
24.1 − 9.15
= 442 ft-kips
Use W21×48 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 5: dead load is 0.7 kips/ft, live load is 1.4 kips/ft, span is 28 ft, the beam has lateral
support at the ends and midspan, and Fy = 60 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.7 + beam wt) + 1.6(1.4) ≈ 3.08 kips/ft
3.08(28)2
wu L2
=
= 302 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of
the beam. Use the segment from 0 ft to 14 ft with Lb = 14 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 14 ft.
Mu 50 ksi
302 50
Required φb Mn =
=
= 194 ft-kips
Cb
Fy
1.30 60
Select: W14×43, φb Mn = 208 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 302 +
1.2(beam wt)L2
1.2(43/1000)(28)2
= 302 +
= 307 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 37.4 ≤ λp = 3.76
= 82.7 ;
= 8.35
= 7.54 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (60)(69.6)/12 = 348 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
1.89
29000
= 1.76
Lp = 1.76ry
= 6.09 ft
Fy
12
60
sp
sp
Iy Cw
(45.2)(1950)
= 2.18 in.
rts =
=
Sx
62.6
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
2.18 29000
(1.05)(1) t
0.7(60) (62.6)(13.1) 2
= 1.95
1 + 1 + 6.76
12 0.7(60) (62.6)(13.1)
29000 (1.05)(1)
= 17.7 ft
Lp = 6.09 ft < [Lb = 14 ft] ≤ [Lr = 17.7 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
14 − 6.09
0.7(60)(62.6)
= (1.30) 348 − 348 −
12
17.7 − 6.09
= 338 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(338) = 304 ft-kips
The W14×43 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
W14×43
W14×48
W21×48
Mu
φb Mn
ft-kips
ft-kips
307
307
307
304†
350†
404†
bf
2tf
h
tw
OKAY?
7.54
6.75
9.47∗
37.4
33.6
53.6
NG
OK
OK
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
W21×44
307
244‡
W18×46
307
259‡
W16×45
307
310†
W16×40
307
268†
W14×43
307
304†
W14×38
306
230†
W12×45
307
289
† Inelastic lateral torsional buckling controls
7.22
5.01
6.23
6.93
7.54
6.57
7
53.6
44.6
41.1
46.5
37.4
39.6
29.6
NG
NG
OK
NG
NG
NG
NG
‡
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked (see below)
For the limit state of compression flange local buckling, AISC–F3.2, for W21×48:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
9.47 − 8.35
0.7(60)(93)
= 535 − 535 −
12
22.0 − 8.35
= 518 ft-kips
∗
Use W16×45 with Fy = 60 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 6: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has
continuous lateral support, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
Since the beam has continous lateral support, Cb = 1.0.
(c) Since the unbraced length is relatively short, select a beam using Table 3-2 Selection
by Zx , AISC Manual, pp. 3-11 to 3-19. Assume λ ≤ λp for a compact section.
Mu
(276)(12)
Required Zx =
= 73.5 in.3
=
φb Fy
(0.9)(50)
Select: W18×40, Zx = 78.4 in.3
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(40/1000)(35)2
= 276 +
= 283 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 50.9 ≤ λp = 3.76
= 90.6 ;
= 5.73 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(78.4)/12 = 327 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
The beam has continuous lateral support, so [Lb = 0] < Lp and lateral torsional
buckling does not apply, AISC-F2.1(a).
Yielding controls! Calculate the design moment strength.
φb Mn = (0.9)(327) = 294 ft-kips
The W18×40 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 40 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W18×40
W16×40
Mu
φb Mn
ft-kips
ft-kips
283
283
294
274
bf
2tf
h
tw
OKAY?
5.73
6.93
50.9
46.5
OK
NG
Use W18×40 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 7: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support every 7 feet, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 7 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 14 ft to 21 ft with Lb = 7 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.990M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.990M
12.5M
Cb =
(1.0) = 1.00
2.5M + 3(0.990M ) + 4(1.0M ) + 3(0.990M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 7 ft.
Mu
276
Required φb Mn =
=
= 274 ft-kips
Cb
1.00
Select: W21×44, φb Mn = 315 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(44/1000)(35)2
1.2(beam wt)L2
= 276 +
= 284 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.6 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 7.22 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(95.4)/12 = 398 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-17, Lp = 4.45 ft and Lr = 13.0 ft.
Lp = 4.45 ft < [Lb = 7 ft] ≤ [Lr = 13.0 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(81.6)
7 − 4.45
= (1.00) 398 − 398 −
12
13.0 − 4.45
= 352 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(352) = 316 ft-kips
The W21×44 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 44 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W21×44
284
316†
W18×40
283
262†
W16×40
283
260†
W14×43
284
260†
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
7.22
5.73
6.93
7.54
53.6
50.9
46.5
37.4
OK
NG
NG
NG
Use W21×44 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 8: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support at the ends and midspan, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of the
beam. Use the segment from 0 ft to 17.5 ft with Lb = 17.5 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 17.5 ft.
Mu
276
Required φb Mn =
=
= 212 ft-kips
Cb
1.30
Select: W21×48, φb Mn = 221 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(48/1000)(35)2
1.2(beam wt)L2
= 276 +
= 284 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.6 ≤ λp = 3.76
= 90.6 ; λp = 0.38
= 9.15 <
= 9.47 ≤
tw
Fy
Fy
2tf
s
#
"
E
= 24.1
λp = 1.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-17, Lp = 5.86 ft and Lr = 16.6 ft.
[Lr = 16.6 ft] < [Lb = 17.5 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
2
Cb π E
Lb
Jc
Mn = Fcr Sx = Sx
1 + 0.078
2
Sx ho rts
(Lb /rts )
s
(1.30)π 2(29000)
(0.803)(1) 12(17.5) 2
= (93)
1 + 0.078
(93)(20.2)
2.05
(12(17.5)/2.05)2
= 319 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(50)(93)
9.47 − 9.15
= 446 − 446 −
12
24.1 − 9.15
= 442 ft-kips
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(319) = 287 ft-kips
The W21×48 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 48 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W21×48
284
287‡
W21×44
284
168‡
W18×46
284
185‡
W16×45
284
227‡
W14×48
284
275†
† Inelastic lateral torsional buckling controls
‡
bf
2tf
h
tw
OKAY?
9.47∗
7.22
5.01
6.23
6.75
53.6
53.6
44.6
41.1
33.6
OK
NG
NG
NG
NG
Elastic lateral torsional buckling controls
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
∗
Flange local buckling limit state must be checked
Use W21×48 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 9: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has
continuous lateral support, and Fy = 65 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
Since the beam has continous lateral support, Cb = 1.0.
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 0 ft.
Mu 50 ksi
276 50
Required φb Mn =
=
= 212 ft-kips
Cb
Fy
1.00 65
Select: W18×35, φb Mn = 249 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(35/1000)(35)2
= 276 +
= 282 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.5 ≤ λp = 3.76
= 79.4 ;
= 7.06 ≤ λp = 0.38
= 8.03
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (65)(66.5)/12 = 360 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
The beam has continuous lateral support, so [Lb = 0] < Lp and lateral torsional
buckling does not apply, AISC-F2.1(a).
Yielding controls! Calculate the design moment strength.
φb Mn = (0.9)(360) = 324 ft-kips
The W18×35 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 35 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W18×35
W16×31
W14×34
W12×35
Mu
φb Mn
ft-kips
ft-kips
282
281
282
282
324
263
266
250
bf
2tf
h
tw
OKAY?
7.06
6.28
7.41
6.31
53.5
51.6
43.1
36.2
OK
NG
NG
NG
Use W18×35 with Fy = 65 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 10: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support every 7 feet, and Fy = 65 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 7 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 14 ft to 21 ft with Lb = 7 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.990M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.990M
12.5M
Cb =
(1.0) = 1.00
2.5M + 3(0.990M ) + 4(1.0M ) + 3(0.990M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 7 ft.
Mu 50 ksi
276 50
Required φb Mn =
=
= 211 ft-kips
Cb
Fy
1.00 65
Select: W18×35, φb Mn = 217 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(35/1000)(35)2
= 276 +
= 282 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.5 ≤ λp = 3.76
= 79.4 ;
= 8.03
= 7.06 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (65)(66.5)/12 = 360 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
1.22
29000
= 1.76
Lp = 1.76ry
= 3.78 ft
Fy
12
65
sp
sp
Iy Cw
(15.3)(1140)
= 1.51 in.
rts =
=
Sx
57.6
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
1.51 29000
(0.506)(1) t
0.7(65) (57.6)(17.3) 2
= 1.95
1 + 1 + 6.76
12 0.7(65) (57.6)(17.3)
29000 (0.506)(1)
= 10.7 ft
Lp = 3.78 ft < [Lb = 7 ft] ≤ [Lr = 10.7 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
7 − 3.78
0.7(65)(57.6)
= (1.00) 360 − 360 −
12
10.7 − 3.78
= 295 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(295) = 266 ft-kips
The W18×35 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
W18×35
W18×40
W16×40
Mu
φb Mn
ft-kips
ft-kips
282
283
283
266†
321†
324†
bf
2tf
h
tw
OKAY?
7.06
5.73
6.93
53.5
50.9
46.5
NG
OK
OK
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
W16×36
282
281†
8.12∗
48.1
NG
†
W16×31
281
212
6.28
51.6
NG
W14×38
283
273†
6.57
39.6
NG
W12×40
283
270†
7.77
33.6
NG
†
W12×35
282
224
6.31
36.2
NG
† Inelastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked (see below)
For the limit state of compression flange local buckling, AISC–F3.2, for W16×36:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(65)(56.5)
8.12 − 8.03
= 347 − 347 −
12
21.1 − 8.03
= 346 ft-kips
Use W16×40 with Fy = 65 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 11: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support at the ends and midspan, and Fy = 65 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of the
beam. Use the segment from 0 ft to 17.5 ft with Lb = 17.5 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 17.5 ft.
Mu 50 ksi
276 50
Required φb Mn =
=
= 163 ft-kips
Cb
Fy
1.30 65
Select: W14×43, φb Mn = 182 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(43/1000)(35)2
= 276 +
= 284 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 37.4 ≤ λp = 3.76
= 79.4 ;
= 8.03
= 7.54 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (65)(69.6)/12 = 377 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
1.89
29000
= 1.76
Lp = 1.76ry
= 5.86 ft
Fy
12
65
sp
sp
Iy Cw
(45.2)(1950)
= 2.18 in.
rts =
=
Sx
62.6
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
2.18 29000
(1.05)(1) t
0.7(65) (62.6)(13.1) 2
= 1.95
1 + 1 + 6.76
12 0.7(65) (62.6)(13.1)
29000 (1.05)(1)
= 16.8 ft
[Lr = 16.8 ft] < [Lb = 17.5 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
2
Jc
Lb
Cb π E
Mn = Fcr Sx = Sx
1 + 0.078
2
Sx ho rts
(Lb /rts )
s
(1.30)π 2(29000)
(1.05)(1)
12(17.5) 2
= (62.6)
1 + 0.078
(62.6)(13.1)
2.18
(12(17.5)/2.18)2
= 290 ft-kips
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(290) = 261 ft-kips
The W14×43 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
W14×43
W14×48
W21×48
Mu
φb Mn
ft-kips
ft-kips
284
284
284
261‡
312†
287‡
bf
2tf
h
tw
OKAY?
7.54
6.75
9.47∗
37.4
33.6
53.6
NG
OK
OK
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
W21×44
284
168‡
W18×46
284
185‡
W16×45
284
227‡
W16×31
281
86.8‡
W14×48
284
312†
W14×43
284
261‡
W14×38
283
166‡
W12×45
284
268†
W12×35
282
145‡
W10×45
284
252†
† Inelastic lateral torsional buckling controls
7.22
5.01
6.23
6.28
6.75
7.54
6.57
7
6.31
6.47
53.6
44.6
41.1
51.6
33.6
37.4
39.6
29.6
36.2
22.5
NG
NG
NG
NG
OK
NG
NG
NG
NG
NG
‡
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked (see below)
For the limit state of compression flange local buckling, AISC–F3.2, for W21×48:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
9.47 − 8.03
0.7(65)(93)
= 580 − 580 −
12
21.1 − 8.03
= 555 ft-kips
∗
Use W14×48 with Fy = 65 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 12: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has
continuous lateral support, and Fy = 100 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
Since the beam has continous lateral support, Cb = 1.0.
(c) Since the unbraced length is relatively short, select a beam using Table 3-2 Selection
by Zx , AISC Manual, pp. 3-11 to 3-19. Assume λ ≤ λp for a compact section.
Mu
(276)(12)
Required Zx =
= 36.8 in.3
=
φb Fy
(0.9)(100)
Select: W12×26, Zx = 37.2 in.3
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(26/1000)(35)2
= 276 +
= 280 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-24 and 1-25.
s
s
# "
# "
#
"
bf
h
E
E
= 47.2 ≤ λp = 3.76
= 64.0 ; λp = 0.38
= 6.47 <
= 8.54 ≤
tw
Fy
Fy
2tf
s
"
#
E
λp = 1.0
= 17.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
The beam has continuous lateral support, so [Lb = 0] < Lp and lateral torsional
buckling does not apply, AISC-F2.1(a).
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(100)(33.4)
8.54 − 6.47
= 310 − 310 −
12
17.0 − 6.47
= 287 ft-kips
Flange local buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(287) = 259 ft-kips
The W12×26 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
W12×26
280
259‡
8.54∗
W14×26
280
302
5.98
‡
W16×26
280
313
7.97∗
W14×26
280
302
5.98
W14×22
280
240‡
7.46∗
‡
W12×26
280
259
8.54∗
‡ Elastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked
h
tw
OKAY?
47.2
48.1
56.8
48.1
53.3
47.2
NG
OK
OK
OK
NG
NG
Use W14×26 with Fy = 100 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 13: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support every 7 feet, and Fy = 100 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 7 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 14 ft to 21 ft with Lb = 7 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.990M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.990M
12.5M
Cb =
(1.0) = 1.00
2.5M + 3(0.990M ) + 4(1.0M ) + 3(0.990M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 7 ft.
Mu 50 ksi
276 50
Required φb Mn =
=
= 137 ft-kips
Cb
Fy
1.00 100
Select: W16×26, φb Mn = 138 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(26/1000)(35)2
= 276 +
= 280 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-20 and 1-21.
s
s
# "
# "
#
"
bf
h
E
E
= 56.8 ≤ λp = 3.76
= 64.0 ; λp = 0.38
= 6.47 <
= 7.97 ≤
tw
Fy
Fy
2tf
s
#
"
E
= 17.0
λp = 1.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
s
r
1.12
E
29000
Lp = 1.76ry
= 1.76
= 2.80 ft
Fy
12
100
sp
sp
Iy Cw
(9.59)(565)
rts =
=
= 1.38 in.
Sx
38.4
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
1 + 1 + 6.76
Lr = 1.95rts
0.7Fy Sx ho
E
Jc
v
s
s
u
u
0.7(100) (38.4)(15.3) 2
1.38
29000
(0.262)(1) t
1 + 1 + 6.76
= 1.95
12 0.7(100) (38.4)(15.3)
29000 (0.262)(1)
= 7.65 ft
Lp = 2.80 ft < [Lb = 7 ft] ≤ [Lr = 7.65 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(100)(38.4)
7 − 2.80
= (1.00) 368 − 368 −
12
7.65 − 2.80
= 245 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(100)(38.4)
7.97 − 6.47
= 368 − 368 −
12
17.0 − 6.47
= 348 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(245) = 220 ft-kips
The W16×26 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
W16×26
280
220†
7.97∗
W16×31
281
280†
6.28
W16×36
282
391†
8.12∗
†
W18×35
282
356
7.06∗
W16×31
281
280†
6.28
W14×34
282
335†
7.41∗
†
W14×30
281
286
5.74
†
W14×26
280
196
5.98
W12×30
281
264†
7.41∗
†
W10×30
281
218
5.7
† Inelastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked
h
tw
OKAY?
56.8
51.6
48.1
53.5
51.6
43.1
45.4
48.1
41.8
29.5
NG
NG
OK
OK
NG
OK
OK
NG
NG
NG
Use W14×30 with Fy = 100 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 14: dead load is 0.3 kips/ft, live load is 0.9 kips/ft, span is 35 ft, the beam has lateral
support at the ends and midspan, and Fy = 100 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.3 + beam wt) + 1.6(0.9) ≈ 1.8 kips/ft
1.8(35)2
wu L2
=
= 276 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and midspan. The loading is uniform and
symmetric, so the worst loading will occur on a segment containing the midpoint of the
beam. Use the segment from 0 ft to 17.5 ft with Lb = 17.5 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.438M
MB = moment at 1/2 pt of the unbraced segment = 0.8M
MC = moment at 3/4 pt of the unbraced segment = 0.938M
12.5M
Cb =
(1.0) = 1.30
2.5M + 3(0.438M ) + 4(0.8M ) + 3(0.938M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 17.5 ft.
Mu 50 ksi
276 50
Required φb Mn =
=
= 106 ft-kips
Cb
Fy
1.30 100
Select: W10×33, φb Mn = 107 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 276 +
1.2(beam wt)L2
1.2(33/1000)(35)2
= 276 +
= 282 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-24 and 1-25.
s
s
# "
# "
#
"
bf
h
E
E
= 27.1 ≤ λp = 3.76
= 64.0 ; λp = 0.38
= 6.47 <
= 9.15 ≤
tw
Fy
Fy
2tf
s
#
"
E
= 17.0
λp = 1.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
s
r
1.94
E
29000
Lp = 1.76ry
= 1.76
= 4.85 ft
Fy
12
100
sp
sp
Iy Cw
(36.6)(791)
rts =
=
= 2.20 in.
Sx
35
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
1 + 1 + 6.76
Lr = 1.95rts
0.7Fy Sx ho
E
Jc
v
s
s
u
u
0.7(100) (35)(9.3) 2
2.20
29000
(0.583)(1) t
1 + 1 + 6.76
= 1.95
12 0.7(100) (35)(9.3)
29000 (0.583)(1)
= 13.5 ft
[Lr = 13.5 ft] < [Lb = 17.5 ft] elastic lateral torsional buckling applies, AISC-F2.1(c).
s
2
2
Jc
Lb
Cb π E
Mn = Fcr Sx = Sx
1 + 0.078
2
Sx ho rts
(Lb /rts )
s
(1.30)π 2(29000)
(0.583)(1) 12(17.5) 2
= (35)
1 + 0.078
(35)(9.3)
2.2
(12(17.5)/2.2)2
= 179 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(100)(35)
9.15 − 6.47
= 323 − 323 −
12
17.0 − 6.47
= 293 ft-kips
Elastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(179) = 161 ft-kips
The W10×33 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
W10×33
282
161‡
9.15∗
W10×39
283
219‡
7.53∗
‡
W10×45
284
285
6.47
W21×44
284
168‡
7.22∗
W18×40
283
147‡
5.73
W16×45
284
227‡
6.23
W16×31
281
86.8‡
6.28
‡
W14×43
284
261
7.54∗
‡
W14×38
283
166
6.57∗
‡
W14×26
280
60.6
5.98
‡
W12×45
284
276
7∗
‡
W12×35
282
145
6.31
W10×45
284
285‡
6.47
‡
W10×39
283
219
7.53∗
W10×30
281
99.2‡
5.7
W8×40
283
229‡
7.21∗
‡ Elastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked
h
tw
OKAY?
27.1
25
22.5
53.6
50.9
41.1
51.6
37.4
39.6
48.1
29.6
36.2
22.5
25
29.5
17.6
NG
NG
OK
NG
NG
NG
NG
NG
NG
NG
NG
NG
OK
NG
NG
NG
Use W10×45 with Fy = 100 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 15: dead load is 0 kips/ft, live load is 1 kips/ft, span is 35 ft, the beam has lateral
support every 5 feet, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0 + beam wt) + 1.6(1) ≈ 1.6 kips/ft
1.6(35)2
wu L2
=
= 245 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 5 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 15 ft to 20 ft with Lb = 5 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.995M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.995M
12.5M
Cb =
(1.0) = 1.00
2.5M + 3(0.995M ) + 4(1.0M ) + 3(0.995M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 5 ft.
Mu
245
Required φb Mn =
=
= 244 ft-kips
Cb
1.00
Select: W16×40, φb Mn = 274 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 245 +
1.2(40/1000)(35)2
1.2(beam wt)L2
= 245 +
= 252 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-20 and 1-21.
s
s
# "
# "
#
"
bf
h
E
E
= 46.5 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 6.93 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(73)/12 = 304 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 W Shapes p. 3-17, Lp = 5.55 ft and Lr =
15.9 ft.
[Lb = 5 ft] ≤ Lp = 5.55 ft lateral torsional buckling does not apply, AISCF2.1(a).
Yielding controls! Calculate the design moment strength.
φb Mn = (0.9)(304) = 274 ft-kips
The W16×40 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 40 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W16×40
252
274
W18×40
252
288†
W18×35
251
242†
W16×40
252
274
W16×36
252
240
W14×38
252
231
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
6.93
5.73
7.06
6.93
8.12
6.57
46.5
50.9
53.5
46.5
48.1
39.6
OK
OK
NG
OK
NG
NG
Use W16×40 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 16: dead load is 0 kips/ft, live load is 1 kips/ft, span is 35 ft, the beam has lateral
support at the ends only, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0 + beam wt) + 1.6(1) ≈ 1.6 kips/ft
1.6(35)2
wu L2
=
= 245 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends only. The longest unbraced length is Lb =
35 ft. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.750M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.750M
12.5M
Cb =
(1.0) = 1.14
2.5M + 3(0.750M ) + 4(1.0M ) + 3(0.750M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 35 ft.
Mu
245
Required φb Mn =
=
= 216 ft-kips
Cb
1.14
Select: W12×65, φb Mn = 231 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 245 +
1.2(65/1000)(35)2
1.2(beam wt)L2
= 245 +
= 257 ft-kips
8
8
(e) Compute the design moment strength using the beam properties from the AISC
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 24.9 ≤ λp = 3.76
= 90.6 ; λp = 0.38
= 9.15 <
= 9.92 ≤
tw
Fy
Fy
2tf
s
"
#
E
= 24.1
λp = 1.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-17, Lp = 10.7 ft and Lr = 35.1 ft.
Lp = 10.7 ft < [Lb = 35 ft] ≤ [Lr = 35.1 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(87.9)
35 − 10.7
= (1.14) 403 − 403 −
12
35.1 − 10.7
= 292 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(50)(87.9)
9.92 − 9.15
= 403 − 403 −
12
24.1 − 9.15
= 396 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(292) = 263 ft-kips
The W12×65 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 65 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W12×65
W24×62
W21×62
W21×57
W18×65
W18×46
W16×57
W14×61
Mu
φb Mn
ft-kips
ft-kips
257
256
256
255
257
253
255
256
263†
104‡
143‡
103‡
155‡
65.9‡
122‡
202‡
bf
2tf
h
tw
OKAY?
9.92∗
5.97
6.7
5.04
5.06
5.01
4.98
7.75
24.9
50.1
46.9
46.3
35.7
44.6
33
30.4
OK
NG
NG
NG
NG
NG
NG
NG
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
W14×53
255
132‡
W14×38
252
58.5‡
W12×65
257
263†
W12×58
256
192‡
W12×50
254
121‡
W10×60
256
206†
W8×58
256
174†
† Inelastic lateral torsional buckling controls
‡
∗
6.11
6.57
9.92∗
7.82
6.31
7.41
5.07
30.9
39.6
24.9
27
26.8
18.7
12.4
NG
NG
OK
NG
NG
NG
NG
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked
Use W12×65 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 17: dead load is 0.7 kips/ft, live load is 2.8 kips/ft, span is 48 ft, the beam has lateral
support every 16 feet, and Fy = 50 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.7 + beam wt) + 1.6(2.8) ≈ 5.32 kips/ft
5.32(48)2
wu L2
=
= 1530 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 16 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 16 ft to 32 ft with Lb = 16 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.972M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.972M
12.5M
Cb =
(1.0) = 1.01
2.5M + 3(0.972M ) + 4(1.0M ) + 3(0.972M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 16 ft.
Mu
1530
Required φb Mn =
=
= 1510 ft-kips
Cb
1.01
Select: W36×135, φb Mn = 1550 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 1530 +
1.2(135/1000)(48)2
1.2(beam wt)L2
= 1530 +
= 1580 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-12 and 1-13.
s
s
# "
# "
#
"
bf
h
E
E
= 54.1 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 7.56 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(509)/12 = 2120 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From Table 3-2 in the AISC Manual p. 3-14, Lp = 8.41 ft and Lr = 24.2 ft.
Lp = 8.41 ft < [Lb = 16 ft] ≤ [Lr = 24.2 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(439)
16 − 8.41
= (1.01) 2120 − 2120 −
12
24.2 − 8.41
= 1740 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(1740) = 1570 ft-kips
The W36×135 beam is not sufficient. Check heavier sections at the same depth. The
following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W36×135
W36×150
W40×149
W36×135
W33×141
W33×130
W30×132
W27×129
W24×131
† Inelastic lateral
1580
1570†
1580
1830†
1580
1810†
1580
1570†
1580
1610†
1580
1440†
1580
1330†
1580
1210†
1580
1270†
torsional buckling controls
bf
2tf
h
tw
OKAY?
7.56
6.37
7.11
7.56
6.01
6.73
5.27
4.55
6.7
54.1
51.9
54.3
54.1
49.6
51.7
43.9
39.7
35.6
NG
OK
OK
NG
OK
NG
NG
NG
NG
Use W33×141 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.3. Select the lightest W section as a beam. Assume only flexure must be considered;
i.e., omit treating shear and deflection. The dead load given is in addition to the weight
of the beam.
Case 18: dead load is 0.7 kips/ft, live load is 2.8 kips/ft, span is 48 ft, the beam has lateral
support every 16 feet, and Fy = 60 ksi.
Use LRFD Design Method
(a) Obtain factored loads:
wu = 1.2(0.7 + beam wt) + 1.6(2.8) ≈ 5.32 kips/ft
5.32(48)2
wu L2
=
= 1530 ft-kips (without beam)
Mu =
8
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support every 16 feet. The loading is uniform and symmetric,
so the worst loading will occur on a segment containing the midpoint of the beam.
Use the segment from 16 ft to 32 ft with Lb = 16 ft. For doubly symmetric members,
Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
Mmax = max moment in the unbraced segment = M
MA = moment at 1/4 pt of the unbraced segment = 0.972M
MB = moment at 1/2 pt of the unbraced segment = 1.0M
MC = moment at 3/4 pt of the unbraced segment = 0.972M
12.5M
Cb =
(1.0) = 1.01
2.5M + 3(0.972M ) + 4(1.0M ) + 3(0.972M )
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 16 ft.
Mu 50 ksi
1530 50
Required φb Mn =
=
= 1260 ft-kips
Cb
Fy
1.01 60
Select: W33×130, φb Mn = 1420 ft-kips
(d) Correct the moment for the selected beam weight.
Mu = 1530 +
1.2(beam wt)L2
1.2(130/1000)(48)2
= 1530 +
= 1580 ft-kips
8
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-12 and 1-13.
s
s
# "
# "
#
"
bf
h
E
E
= 51.7 ≤ λp = 3.76
= 82.7 ;
= 8.35
= 6.73 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (60)(467)/12 = 2340 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
2.39
29000
= 1.76
Lp = 1.76ry
= 7.71 ft
Fy
12
60
sp
sp
Iy Cw
(218)(56600)
= 2.94 in.
rts =
=
Sx
406
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
2.94 29000
(7.37)(1) t
0.7(60) (406)(32.2) 2
= 1.95
1 + 1 + 6.76
12 0.7(60) (406)(32.2)
29000 (7.37)(1)
= 21.8 ft
Lp = 7.71 ft < [Lb = 16 ft] ≤ [Lr = 21.8 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
16 − 7.71
0.7(60)(406)
= (1.01) 2340 − 2340 −
12
21.8 − 7.71
= 1820 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.9)(1820) = 1640 ft-kips
The W33×130 beam is sufficient. To verify it is the lightest beam use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 130 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W33×130
W30×124
Mu
φb Mn
ft-kips
ft-kips
1580
1580
1640†
1390†
bf
2tf
h
tw
OKAY?
6.73
5.65
51.7
46.2
OK
NG
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
W27×129
W24×117
W21×122
† Inelastic lateral
1580
1370†
1570
1280†
1570
1220†
torsional buckling controls
4.55
7.53
6.45
39.7
39.2
31.3
NG
NG
NG
Use W33×130 with Fy = 60 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.4. Select the lightest W sections for the stituation shown in the accompanying figure,
under the following conditions:
(a) A992 steel; continuous lateral support
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.7) + 1.6(3.5) = 6.44 kips/ft
Wu = 1.2(28) + 1.6(7) = 44.8 kips
1
Mu = (6.44)(30)2 + 10(44.8) = 1, 172 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
Since the beam has continous lateral support, Cb = 1.0.
(c) Since the unbraced length is zero, select a beam using Table 3-2 Selection by Zx , AISC
Manual, pp. 3-11 to 3-19. Assume λ ≤ λp for a compact section.
Mu
(1, 172)(12)
= 313 in.3
Required Zx =
=
φb Fy
(0.90)(50)
Select: W30×108, Zx = 346 in.3
(d) Correct the moment for the beam weight.
1
Mu = 1, 172 + (108/1000)(30)2 = 1, 190 ft-kips
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-14 and 1-15.
s
s
# "
# "
#
"
b
h
E
E
f
= 49.6 ≤ λp = 3.76
= 90.6 ;
= 6.89 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Mn = Mp = Fy Zx = (50)(346)/12 = 1, 440 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
The beam has continuous lateral support, so [Lb = 0] < Lp and lateral torsional
buckling does not apply, AISC-F2.1(a).
Yielding controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 440) = 1, 300 ft-kips
The W30×108 beam is sufficient. To verify it is the lightest beam, use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 108 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W30×108
W27×102
W24×104
Mu
φb Mn
ft-kips
ft-kips
1,190
1,190
1,190
1,300
1,140
1,080
bf
2tf
h
tw
OKAY?
6.89
6.03
8.5
49.6
47.1
43.1
OK
NG
NG
Use W30×108 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.4. Select the lightest W sections for the stituation shown in the accompanying figure,
under the following conditions:
(b) A992 steel; lateral support at the ends
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.7) + 1.6(3.5) = 6.44 kips/ft
Wu = 1.2(28) + 1.6(7) = 44.8 kips
1
Mu = (6.44)(30)2 + 10(44.8) = 1, 172 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends. The unbraced length is Lb = 30 ft. For
doubly symmetric members, Rm = 1.0. Use statics to find the moments in the beam:
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5(1, 172)
(1.0) = 1.14
=
2.5(1, 172) + 3(879.4) + 4(1, 172) + 3(879.4)
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 30 ft.
Mu
1, 172
Required φb Mn =
=
= 1, 030 ft-kips
Cb
1.14
Select: W24×146, φb Mn = 1, 070 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 1, 172 + (146/1000)(30)2 = 1, 190 ft-kips
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-16 and 1-17.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
s
s
# "
# "
#
"
bf
h
E
E
= 33.2 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 5.92 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(418)/12 = 1, 740 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-14, Lp = 10.6 ft and Lr = 33.7 ft.
Lp = 10.6 ft < [Lb = 30 ft] ≤ [Lr = 33.7 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
30 − 10.6
0.7(50)(371)
= (1.14) 1, 740 − 1, 740 −
12
33.7 − 10.6
= 1, 350 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 350) = 1, 210 ft-kips
The W24×146 beam is sufficient. To verify it is the lightest beam, use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 146 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W24×146
W36×135
W33×141
W30×132
W27×146
W27×129
W24×146
W24×131
W21×132
W18×143
Mu
φb Mn
ft-kips
ft-kips
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,210†
910‡
994‡
796‡
1,350†
760‡
1,210†
1,030†
973†
1,010†
†
Inelastic lateral torsional buckling controls
‡
Elastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
5.92
7.56
6.01
5.27
7.16
4.55
5.92
6.7
6.01
4.25
33.2
54.1
49.6
43.9
39.4
39.7
33.2
35.6
28.9
22
OK
NG
NG
NG
OK
NG
OK
NG
NG
NG
Use W24×146 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.4. Select the lightest W sections for the stituation shown in the accompanying figure,
under the following conditions:
(c) A992 steel; lateral support at the ends and at 10 ft
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.7) + 1.6(3.5) = 6.44 kips/ft
Wu = 1.2(28) + 1.6(7) = 44.8 kips
1
Mu = (6.44)(30)2 + 10(44.8) = 1, 172 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and at 10 ft. The worst loading and longest
unbraced length occur on the segment from 10 ft to 30 ft with Lb = 20 ft. For doubly
symmetric members, Rm = 1.0. Use statics to find the moments in the beam:
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5(1, 172)
=
(1.0) = 1.15
2.5(1, 172) + 3(1, 172) + 4(1, 092) + 3(626.5)
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 20 ft.
Mu
1, 172
Required φb Mn =
=
= 1, 020 ft-kips
Cb
1.15
Select: W33×118, φb Mn = 1, 080 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 1, 172 + (118/1000)(30)2 = 1, 190 ft-kips
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-12 and 1-13.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
s
s
# "
# "
#
"
bf
h
E
E
= 54.5 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 7.76 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(415)/12 = 1, 730 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-14, Lp = 8.19 ft and Lr = 23.5 ft.
Lp = 8.19 ft < [Lb = 20 ft] ≤ [Lr = 23.5 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
20 − 8.19
0.7(50)(359)
= (1.15) 1, 730 − 1, 730 −
12
23.5 − 8.19
= 1, 390 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 390) = 1, 250 ft-kips
The W33×118 beam is sufficient. To verify it is the lightest beam, use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 118 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
W33×118
W30×116
W27×114
W24×117
†
Mu
φb Mn
ft-kips
ft-kips
1,190
1,190
1,190
1,190
1,250†
1,110†
1,020†
1,160†
bf
2tf
h
tw
OKAY?
7.76
6.17
5.41
7.53
54.5
47.8
42.5
39.2
OK
NG
NG
NG
Inelastic lateral torsional buckling controls
Use W33×118 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.4. Select the lightest W sections for the stituation shown in the accompanying figure,
under the following conditions:
(d) A572 Grade 60 steel; lateral support at the ends and at 10 ft
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.7) + 1.6(3.5) = 6.44 kips/ft
Wu = 1.2(28) + 1.6(7) = 44.8 kips
1
Mu = (6.44)(30)2 + 10(44.8) = 1, 172 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends and at 10 ft. The worst loading and longest
unbraced length occur on the segment from 10 ft to 30 ft with Lb = 20 ft. For doubly
symmetric members, Rm = 1.0. Use statics to find the moments in the beam:
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5(1, 172)
=
(1.0) = 1.15
2.5(1, 172) + 3(1, 172) + 4(1, 092) + 3(626.5)
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 20 ft.
Mu 50 ksi
1, 172 50
Required φb Mn =
=
= 846 ft-kips
Cb
Fy
1.15 60
Select: W24×104, φb Mn = 875 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 1, 172 + (104/1000)(30)2 = 1, 190 ft-kips
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-16 and 1-17.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
s
s
# "
# "
#
"
bf
h
E
E
= 43.1 ≤ λp = 3.76
= 82.7 ; λp = 0.38
= 8.35 <
= 8.5 ≤
tw
Fy
Fy
2tf
s
"
#
E
λp = 1.0
= 22.0
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
s
r
E
2.91
29, 000
= 1.76
Lp = 1.76ry
= 9.38 ft
Fy
12
60
sp
sp
Iy Cw
(259)(35200)
=
rts =
= 3.42 in.
Sx
258
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
3.42 29, 000
(4.72)(1) t
0.7(60) (258)(23.3) 2
= 1.95
1 + 1 + 6.76
12 0.7(60) (258)(23.3)
29, 000 (4.72)(1)
= 26.1 ft
Lp = 9.38 ft < [Lb = 20 ft] ≤ [Lr = 26.1 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
20 − 9.38
0.7(60)(258)
= (1.15) 1, 440 − 1, 440 −
12
26.1 − 9.38
= 1, 270 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(60)(258)
8.5 − 8.35
= 1, 440 − 1, 440 −
12
22.0 − 8.35
= 1, 440 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 270) = 1, 140 ft-kips
The W24×104 beam is not sufficient. Try heavier sections at the same depth. The following
table shows the moment corrected for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
W24×104
W24×117
W30×116
W30×108
W27×114
W24×104
W24×103
W21×111
Mu
φb Mn
ft-kips
ft-kips
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,190
1,140†
1,320†
1,210†
1,060‡
1,120†
1,140†
849‡
1,130†
bf
2tf
h
tw
OKAY?
8.5∗
7.53
6.17
6.89
5.41
8.5∗
4.59
7.05
43.1
39.2
47.8
49.6
42.5
43.1
39.2
34.1
NG
OK
OK
NG
NG
NG
NG
NG
†
Inelastic lateral torsional buckling controls
‡
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked
∗
Use W30×116 with Fy = 60 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.6. Select the lightest W sections for the conditions shown in the accompanying
figure. Assume there is no deflection limitation. Use (a) A992 steel.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.4) + 1.6(1.1) = 2.24 kips/ft
Wu = 1.2(15) + 1.6(15) = 42.0 kips
1
Mu = (2.24)(42)2 + 10(42.0) = 1, 124 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends, at 15 ft, and at 27 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5(1, 084)
=
(1.0) = 1.56 segment A
2.5(1, 084) + 3(318.2) + 4(604.8) + 3(860.0)
12.5(1, 124)
=
(1.0) = 1.00 segment B
2.5(1, 124) + 3(1, 114) + 4(1, 124) + 3(1, 114)
Assume segment B controls.
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 12 ft.
Mu
1, 124
Required φb Mn =
=
= 1, 120 ft-kips
Cb
1.00
Select: W30×108, φb Mn = 1, 140 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 1, 124 + (108/1000)(42)2 = 1, 150 ft-kips
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-14 and 1-15.
s
s
# "
# "
#
"
bf
h
E
E
= 49.6 ≤ λp = 3.76
= 90.6 ;
= 9.15
= 6.89 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(346)/12 = 1, 440 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-15, Lp = 7.59 ft and Lr = 22.0 ft.
Lp = 7.59 ft < [Lb = 12 ft] ≤ [Lr = 22.0 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
≤ Mp
Mn = Cb Mp − Mp − 0.7Fy Sx
Lr − Lp
0.7(50)(299)
12 − 7.59
= (1.00) 1, 440 − 1, 440 −
12
22.0 − 7.59
= 1, 270 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 270) = 1, 150 ft-kips
The W30×108 beam is not sufficient. Try heavier sections at the same depth. The following
table shows the moment corrected for the beam weight.
Section
W30×108
W30×116
W27×114
W24×104
W24×103
W21×111
†
Mu
φb Mn
ft-kips
ft-kips
1,150
1,150
1,150
1,150
1,150
1,150
1,150†
1,260†
1,150†
1,050†
918†
1,020†
bf
2tf
h
tw
OKAY?
6.89
6.17
5.41
8.5
4.59
7.05
49.6
47.8
42.5
43.1
39.2
34.1
NG
OK
NG
NG
NG
NG
bf
2tf
h
tw
OKAY?
6.17
47.8
OK
Inelastic lateral torsional buckling controls
Check segment A
Section
W30×116
Mu
φb Mn
ft-kips
ft-kips
1,110
1,420
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Use W30×116 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.6. Select the lightest W sections for the conditions shown in the accompanying
figure. Assume there is no deflection limitation. Use (b) A572 Grade 60 steel.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
wu = 1.2(0.4) + 1.6(1.1) = 2.24 kips/ft
Wu = 1.2(15) + 1.6(15) = 42.0 kips
1
Mu = (2.24)(42)2 + 10(42.0) = 1, 124 ft-kips
8
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends, at 15 ft, and at 27 ft. For doubly symmetric
members, Rm = 1.0.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5(1, 084)
=
(1.0) = 1.56 segment A
2.5(1, 084) + 3(318.2) + 4(604.8) + 3(860.0)
12.5(1, 124)
=
(1.0) = 1.00 segment B
2.5(1, 124) + 3(1, 114) + 4(1, 124) + 3(1, 114)
Assume segment B controls.
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 12 ft.
Mu 50 ksi
1, 124 50
Required φb Mn =
=
= 933 ft-kips
Cb
Fy
1.00 60
Select: W30×99, φb Mn = 1, 020 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 1, 124 + (99/1000)(42)2 = 1, 150 ft-kips
8
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-14 and 1-15.
s
s
# "
# "
#
"
bf
h
E
E
= 51.9 ≤ λp = 3.76
= 82.7 ;
= 8.35
= 7.8 ≤ λp = 0.38
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (60)(312)/12 = 1, 560 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
2.1
29, 000
= 1.76
Lp = 1.76ry
= 6.77 ft
Fy
12
60
sp
sp
Iy Cw
(128)(26800)
= 2.62 in.
rts =
=
Sx
269
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
u
2.62 29, 000 (3.77)(1) t
0.7(60) (269)(29) 2
= 1.95
1 + 1 + 6.76
12 0.7(60) (269)(29)
29, 000 (3.77)(1)
= 19.3 ft
Lp = 6.77 ft < [Lb = 12 ft] ≤ [Lr = 19.3 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
12 − 6.77
0.7(60)(269)
= (1.00) 1, 560 − 1, 560 −
12
19.3 − 6.77
= 1, 310 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(1, 310) = 1, 180 ft-kips
The W30×99 beam is sufficient. To verify it is the lightest beam, use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 99 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
1,150
1,150
1,150
1,180†
1,060†
948†
W30×99
W27×94
W24×94
†
bf
2tf
h
tw
OKAY?
7.8
6.7
5.18
51.9
49.5
41.9
OK
NG
NG
bf
2tf
h
tw
OKAY?
7.8
51.9
OK
Inelastic lateral torsional buckling controls
Check segment A
Section
W30×99
Mu
φb Mn
ft-kips
ft-kips
1,110
1,400
Use W30×99 with Fy = 60 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.7. A floor beam, laterally supported at the ends only and supporting vibration
inducing heavy machinery, is subject to the loads shown in the accompanying figure. Select
the lightest W section of A992 steel. Compare the result when there is no deflection limit
with that when L/d is limited to a minimum of 20 under full load, a traditional limit to
minimize perceptible vibration due to pedestrian traffic.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Wu = 1.2(0) + 1.6(14)(1.5) = 33.6 kips (includes impact)
Mu = 7(33.6) = 235.2 ft-kips
(b) Determine the Cb factor, AISC-F1.
The beam has lateral support at the ends. For doubly symmetric members, Rm = 1.0.
12.5Mmax
Rm ≤ 3.0
Cb =
2.5Mmax + 3MA + 4MB + 3MC
12.5(235.2)
=
(1.0) = 1.05
2.5(235.2) + 3(210.0) + 4(235.2) + 3(210.0)
(c) Since the unbraced length is fairly long, select a beam using Table 3-10 Available
Moment vs. Unbraced Length, AISC Manual, pp. 3-96 to 3-131 with Lb = 25 ft.
Mu
235.2
Required φb Mn =
=
= 223 ft-kips
Cb
1.05
Select: W12×58, φb Mn = 233 ft-kips
(d) Correct the moment for the beam weight.
1
Mu = 235.2 + (58/1000)(25)2 = 241 ft-kips
8
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-24 and 1-25.
s
s
# "
# "
#
"
bf
h
E
E
= 27 ≤ λp = 3.76
= 90.6 ;
= 7.82 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(86.4)/12 = 360 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-17, Lp = 8.87 ft and Lr = 29.9 ft.
Lp = 8.87 ft < [Lb = 25 ft] ≤ [Lr = 29.9 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(78)
25 − 8.87
= (1.05) 360 − 360 −
12
29.9 − 8.87
= 272 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(272) = 245 ft-kips
The W12×58 beam is sufficient. To verify it is the lightest beam, use Table 1-1 of the
AISC Manual, and examine the first beam in each group lighter than 58 lb/ft with a large
enough Zx . The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W12×58
241
245†
W24×55
240
121‡
W21×55
240
169‡
W21×57
241
148‡
W18×55
240
162‡
W18×46
240
92.4‡
W16×57
241
169‡
W14×53
240
185‡
W14×38
239
82.3‡
W12×50
240
167‡
W10×54
240
200†
W8×58
241
189†
† Inelastic lateral torsional buckling controls
‡
bf
2tf
h
tw
OKAY?
7.82
6.94
7.87
5.04
5.98
5.01
4.98
6.11
6.57
6.31
8.15
5.07
27
54.6
50
46.3
41.1
44.6
33
30.9
39.6
26.8
21.2
12.4
OK
NG
NG
NG
NG
NG
NG
NG
NG
NG
NG
NG
Elastic lateral torsional buckling controls
With no deflection, use W12×58 with Fy = 50 ksi steel.
Considering the L/d deflection limit the minimum depth is d =
following table shows the moment corrected for the beam weight.
25(12)
= 15 in. The
20
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
W16×67
241
336†
W24×62
241
153‡
W21×62
241
213‡
W21×57
241
148‡
W18×65
241
219‡
W18×46
240
92.4‡
W16×57
241
169‡
† Inelastic lateral torsional buckling controls
‡
bf
2tf
h
tw
OKAY?
7.7
5.97
6.7
5.04
5.06
5.01
4.98
35.9
50.1
46.9
46.3
35.7
44.6
33
OK
NG
NG
NG
NG
NG
NG
Elastic lateral torsional buckling controls
With deflection use W16×67 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.8. For the case assigned by the instructor, select the lightest W section to serve as a
uniformly loaded library floor beam on a simply supported beam. Lateral support occurs
at the ends and at L/4, L/2, and 3L/4. Given dead load moment does not include beam
weight. Assume Cb = 1.0.
Case 1: MD = 49 ft-kips, ML = 98 ft-kips, L = 28 ft, Fy = 50 ksi, and the deflection limit
is L/360.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Mu = 1.2MD + 1.6ML = 1.2(49) + 1.6(98) = 216 ft-kips
(b) Obtain the minimum moment of inertia Ix required using the service live load moment.
L
28(12)
∆lim =
=
= 0.933 in.
360
360
5ML L2
(5)(98 × 12)(28 × 12)2
=
= 511 in.4
Min Ix =
48E∆lim
(48)(29, 000)(0.933)
(c) The problem statement says to use Cb = 1.0.
(d) Select a beam using Table 3-10 Available Moment vs.
Manual, pp. 3-96 to 3-131 with Lb = 7 ft.
Mu
215.6
Required φb Mn =
=
= 216 ft-kips
Cb
1.00
Select: W18×35, φb Mn = 217 ft-kips
Unbraced Length, AISC
(e) Correct the moment for the beam weight.
1
Mu = 215.6 + 1.2
(35/1000)(28)2 = 220 ft-kips
8
(f) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.5 ≤ λp = 3.76
= 90.6 ;
= 7.06 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(66.5)/12 = 277 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-18, Lp = 4.31 ft and Lr = 12.4 ft.
Lp = 4.31 ft < [Lb = 7 ft] ≤ [Lr = 12.4 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(57.6)
7 − 4.31
= (1.00) 277 − 277 −
12
12.4 − 4.31
= 241 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(241) = 217 ft-kips
The W18×35 beam does not have sufficient strength. The following table shows the
moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W18×35
220
217†
W18×40
220
261†
W16×36
220
225†
W14×38
220
218†
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
7.06
5.73
8.12
6.57
53.5
50.9
48.1
39.6
NG
OK
OK
NG
(g) Check the beams for deflection.
Section
Ix
in.4
LL Defl.
in.
LL Defl. Limit
in.
OKAY?
W18×35
W18×40
W16×36
W14×38
510
612
448
385
0.935
0.779
1.06
1.24
0.933
0.933
0.933
0.933
NG
OK
NG
NG
Use W18×40 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.8. For the case assigned by the instructor, select the lightest W section to serve as a
uniformly loaded library floor beam on a simply supported beam. Lateral support occurs
at the ends and at L/4, L/2, and 3L/4. Given dead load moment does not include beam
weight. Assume Cb = 1.0.
Case 2: MD = 49 ft-kips, ML = 98 ft-kips, L = 28 ft, Fy = 60 ksi, and the deflection limit
is L/360.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Mu = 1.2MD + 1.6ML = 1.2(49) + 1.6(98) = 216 ft-kips
(b) Obtain the minimum moment of inertia Ix required using the service live load moment.
L
28(12)
∆lim =
=
= 0.933 in.
360
360
5ML L2
(5)(98 × 12)(28 × 12)2
=
= 511 in.4
Min Ix =
48E∆lim
(48)(29, 000)(0.933)
(c) The problem statement says to use Cb = 1.0.
(d) Select a beam using Table 3-10 Available Moment vs. Unbraced Length, AISC
Manual, pp. 3-96 to 3-131 with Lb = 7 ft.
Mu 50 ksi
215.6 50
Required φb Mn =
=
= 180 ft-kips
Cb
Fy
1.00 60
Select: W14×34, φb Mn = 193 ft-kips
(e) Correct the moment for the beam weight.
1
Mu = 215.6 + 1.2
(34/1000)(28)2 = 220 ft-kips
8
(f) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
bf
h
E
E
= 43.1 ≤ λp = 3.76
= 82.7 ;
= 7.41 ≤ λp = 0.38
= 8.35
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (60)(54.6)/12 = 273 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
s
r
E
1.53
29, 000
= 1.76
Lp = 1.76ry
= 4.93 ft
Fy
12
60
sp
sp
Iy Cw
(23.3)(1070)
=
rts =
= 1.80 in.
Sx
48.6
v
s
u
r
u
0.7Fy Sx ho 2
E
Jc t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
1.80 29, 000
(0.569)(1) u
0.7(60) (48.6)(13.5) 2
t
= 1.95
1 + 1 + 6.76
12 0.7(60) (48.6)(13.5)
29, 000 (0.569)(1)
= 13.9 ft
Lp = 4.93 ft < [Lb = 7 ft] ≤ [Lr = 13.9 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
7 − 4.93
0.7(60)(48.6)
= (1.00) 273 − 273 −
12
13.9 − 4.93
= 249 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(249) = 224 ft-kips
The W14×34 beam has sufficient strength. The following table shows the moment corrected
for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W14×34
220
224†
W14×38
220
255†
W16×40
220
302†
W16×36
220
262†
W18×35
220
249†
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
7.41
6.57
6.93
8.12
7.06
43.1
39.6
46.5
48.1
53.5
OK
OK
OK
OK
OK
(g) Check the beams for deflection.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Ix
in.4
LL Defl.
in.
LL Defl. Limit
in.
OKAY?
W14×34
W14×38
W16×40
W16×36
W18×35
340
385
518
448
510
1.40
1.24
0.921
1.06
0.935
0.933
0.933
0.933
0.933
0.933
NG
NG
OK
NG
NG
Use W16×40 with Fy = 60 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.8. For the case assigned by the instructor, select the lightest W section to serve as a
uniformly loaded library floor beam on a simply supported beam. Lateral support occurs
at the ends and at L/4, L/2, and 3L/4. Given dead load moment does not include beam
weight. Assume Cb = 1.0.
Case 3: MD = 0 ft-kips, ML = 240 ft-kips, L = 48 ft, Fy = 50 ksi, and the deflection limit
is L/300.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Mu = 1.2MD + 1.6ML = 1.2(0) + 1.6(240) = 384 ft-kips
(b) Obtain the minimum moment of inertia Ix required using the service live load moment.
L
48(12)
∆lim =
=
= 1.92 in.
300
300
5ML L2
(5)(240 × 12)(48 × 12)2
=
= 1, 790 in.4
Min Ix =
48E∆lim
(48)(29, 000)(1.92)
(c) The problem statement says to use Cb = 1.0.
(d) Select a beam using Table 3-10 Available Moment vs.
Manual, pp. 3-96 to 3-131 with Lb = 12 ft.
Mu
384.0
Required φb Mn =
=
= 384 ft-kips
Cb
1.00
Select: W21×62, φb Mn = 440 ft-kips
Unbraced Length, AISC
(e) Correct the moment for the beam weight.
1
Mu = 384.0 + 1.2
(62/1000)(48)2 = 405 ft-kips
8
(f) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 46.9 ≤ λp = 3.76
= 90.6 ;
= 6.7 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(144)/12 = 600 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-16, Lp = 6.25 ft and Lr = 18.1 ft.
Lp = 6.25 ft < [Lb = 12 ft] ≤ [Lr = 18.1 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(127)
12 − 6.25
= (1.00) 600 − 600 −
12
18.1 − 6.25
= 489 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(489) = 440 ft-kips
The W21×62 beam has sufficient strength. The following table shows the moment corrected
for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W21×62
405
440†
W21×68
408
494†
W21×73
409
536†
W21×83
413
620†
W24×76
410
633†
W24×68
408
549†
W24×62
405
402†
W18×65
406
409†
† Inelastic lateral torsional buckling controls
bf
2tf
h
tw
OKAY?
6.7
6.04
5.6
5
6.61
7.66
5.97
5.06
46.9
43.6
41.2
36.4
49
52
50.1
35.7
OK
OK
OK
OK
OK
OK
NG
OK
(g) Check the beams for deflection.
Section
Ix
in.4
LL Defl.
in.
LL Defl. Limit
in.
OKAY?
W21×62
W21×68
W21×73
W21×83
W24×76
W24×68
W24×62
W18×65
1330
1480
1600
1830
2100
1830
1550
1070
2.58
2.32
2.15
1.88
1.63
1.88
2.21
3.21
1.92
1.92
1.92
1.92
1.92
1.92
1.92
1.92
NG
NG
NG
OK
OK
OK
NG
NG
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Use W24×68 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.8. For the case assigned by the instructor, select the lightest W section to serve as a
uniformly loaded library floor beam on a simply supported beam. Lateral support occurs
at the ends and at L/4, L/2, and 3L/4. Given dead load moment does not include beam
weight. Assume Cb = 1.0.
Case 4: MD = 0 ft-kips, ML = 240 ft-kips, L = 48 ft, Fy = 65 ksi, and the deflection limit
is L/300.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Mu = 1.2MD + 1.6ML = 1.2(0) + 1.6(240) = 384 ft-kips
(b) Obtain the minimum moment of inertia Ix required using the service live load moment.
L
48(12)
∆lim =
=
= 1.92 in.
300
300
5ML L2
(5)(240 × 12)(48 × 12)2
=
= 1, 790 in.4
Min Ix =
48E∆lim
(48)(29, 000)(1.92)
(c) The problem statement says to use Cb = 1.0.
(d) Select a beam using Table 3-10 Available Moment vs. Unbraced Length, AISC
Manual, pp. 3-96 to 3-131 with Lb = 12 ft.
Mu 50 ksi
384.0 50
Required φb Mn =
=
= 295 ft-kips
Cb
Fy
1.00 65
Select: W21×48, φb Mn = 313 ft-kips
(e) Correct the moment for the beam weight.
1
Mu = 384.0 + 1.2
(48/1000)(48)2 = 401 ft-kips
8
(f) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.6 ≤ λp = 3.76
= 79.4 ; λp = 0.38
= 8.03 <
= 9.47 ≤
tw
Fy
Fy
2tf
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
"
λp = 1.0
s
E
= 21.1
Fy
#
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
s
r
E
1.66
29, 000
= 1.76
Lp = 1.76ry
= 5.14 ft
Fy
12
65
sp
sp
Iy Cw
(38.7)(3950)
=
rts =
= 2.05 in.
Sx
93
v
s
u
r
0.7Fy Sx ho 2
E
Jc u
t
Lr = 1.95rts
1 + 1 + 6.76
0.7Fy Sx ho
E
Jc
v
s
s
u
0.7(65) (93)(20.2) 2
2.05 29, 000 (0.803)(1) u
t
= 1.95
1 + 1 + 6.76
12 0.7(65) (93)(20.2)
29, 000 (0.803)(1)
= 14.3 ft
Lp = 5.14 ft < [Lb = 12 ft] ≤ [Lr = 14.3 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(65)(93)
12 − 5.14
= (1.00) 580 − 580 −
12
14.3 − 5.14
= 409 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
9.47 − 8.03
0.7(65)(93)
= 580 − 580 −
12
21.1 − 8.03
= 555 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(409) = 369 ft-kips
The W21×48 beam does not have sufficient strength. The following table shows the
moment corrected for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
h
tw
W21×48
401
369†
9.47∗
53.6
†
W21×83
413
748
5
36.4
W24×76
410
764†
6.61
49
W24×68
408
662†
7.66
52
W24×62
405
461†
5.97
50.1
W18×65
406
488†
5.06
35.7
† Inelastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked (see below)
OKAY?
NG
OK
OK
OK
OK
OK
(g) Check the beams for deflection.
Section
Ix
in.4
LL Defl.
in.
LL Defl. Limit
in.
OKAY?
W21×48
W21×83
W24×76
W24×68
W24×62
W18×65
959
1830
2100
1830
1550
1070
3.58
1.88
1.63
1.88
2.21
3.21
1.92
1.92
1.92
1.92
1.92
1.92
NG
OK
OK
OK
NG
NG
Use W24×68 with Fy = 65 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.13, Part a. Select the lightest W section for the situation shown in the accompanying
figure. The concentrated load W is 5 kips dead load and 15 kips live load. Assume lateral
support is provided at the reactions and the concentrated loads. Use A992 steel.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
The maximum moment is at the support.
Wu = 1.2(5) + 1.6(15) = 30.0 kips
1
Mu = (beam wt.)(10)2 + 10Wu = 10(30.0) = 300.0 ft-kips w/o beam
2
(b) Determine the Cb factor, AISC-F1.
The moment is uniform over the 30 ft span, so Cb = 1.0.
(c) Select a beam using Table 3-10 Available Moment vs.
Manual, pp. 3-96 to 3-131 with Lb = 30 ft.
300.0
Mu
=
= 300 ft-kips
Required φb Mn =
Cb
1.00
Select: W14×74, φb Mn = 302 ft-kips
Unbraced Length, AISC
(d) Correct the moment for the beam weight.
1
Mu = 300.0 + 1.2
(74/1000)(10)2 = 304 ft-kips
2
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-22 and 1-23.
s
s
# "
# "
#
"
b
h
E
E
f
= 25.4 ≤ λp = 3.76
= 90.6 ;
= 6.41 ≤ λp = 0.38
= 9.15
tw
Fy
2tf
Fy
The web is compact and the flange is compact so use AISC-F2.
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(126)/12 = 525 ft-kips
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-17, Lp = 8.76 ft and Lr = 31.0 ft.
Lp = 8.76 ft < [Lb = 30 ft] ≤ [Lr = 31.0 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(112)
30 − 8.76
= (1.00) 525 − 525 −
12
31.0 − 8.76
= 336 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(336) = 302 ft-kips
The W14×74 beam does not have sufficient strength. The following table shows the
moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
W14×74
304
302†
W14×82
305
348†
W12×79
305
337†
W12×72
304
297†
W16×77
305
317‡
W16×67
304
251‡
W18×76
305
329‡
W18×71
304
192‡
† Inelastic lateral torsional buckling controls
‡
bf
2tf
h
tw
OKAY?
6.41
5.92
8.22
8.99
6.77
7.7
8.11
4.71
25.4
22.4
20.7
22.6
31.2
35.9
37.8
32.4
NG
OK
OK
NG
OK
NG
OK
NG
Elastic lateral torsional buckling controls
Use W18×76 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
9.13, Part b. Select the lightest W section for the situation shown in the accompanying
figure. The concentrated load W is 5 kips dead load and 15 kips live load. Assume lateral
support is provided at the reactions and the concentrated loads. Use A992 steel.
Use LRFD Design Method
(a) Obtain the factored loads (neglecting the beam weight):
Wu = 1.2(5) = 6.00 kips (dead load only)
Wu = 1.2(5) + 1.6(15) = 60.0 kips
There are two loading cases:
For Loading Case 1, live load is on the span but not on the cantilevers. Maximum
moment at midspan.
1
(60.0)(30)
= 390 ft-kips
Mu = (beam wt.)(302 − 102 ) − (6.00)(10) +
8
4
For Loading Case 2, live load is on the cantilevers but not on the 30 ft span. Maximum
moment at the supports.
1
Mu = (beam wt.)(10)2 + (30.0)(10) = 300 ft-kips
2
(b) Determine the Cb factor, AISC-F1. For the 30 ft span in Case 1:
12.5Mmax
Cb =
2.5Mmax + 3MA + 4MB + 3MC
12.5(390)
=
= 1.86
2.5(390) + 3(52.5) + 4(165) + 3(278)
For the 30 ft span in Case 2:
12.5(300)
Cb =
= 1.14
2.5(300) + 3(278) + 4(255) + 3(232)
Assume Case 2 controls.
(c) Select a beam using Table 3-10 Available Moment vs. Unbraced Length, AISC
Manual, pp. 3-96 to 3-131 with Lb = 15 ft.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Mu
300.0
=
= 264 ft-kips
Cb
1.14
Select: W21×48, φb Mn = 268 ft-kips
Required φb Mn =
(d) Correct the moment for the beam weight.
1
(48/1000)(10)2 = 303 ft-kips
Mu = 300.0 + 1.2
2
(e) Compute the design moment strength using the beam properties from the AISC
Manual Table 1-1, pp. 1-18 and 1-19.
s
s
# "
# "
#
"
bf
h
E
E
= 53.6 ≤ λp = 3.76
= 90.6 ; λp = 0.38
= 9.15 <
= 9.47 ≤
tw
Fy
Fy
2tf
s
"
#
E
λp = 1.0
= 24.1
Fy
The web is compact and the flange is noncompact so use AISC-F3.
For the limit state of lateral torsional buckling, AISC-F3.1 uses AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-17, Lp = 6.09 ft and Lr = 16.6 ft.
Lp = 6.09 ft < [Lb = 15 ft] ≤ [Lr = 16.6 ft] inelastic lateral torsional buckling
applies, AISC-F2.1(b).
Lb − Lp
Mn = Cb Mp − Mp − 0.7Fy Sx
≤ Mp
Lr − Lp
0.7(50)(93)
15 − 6.09
= (1.14) 446 − 446 −
12
16.6 − 6.09
= 338 ft-kips
For the limit state of compression flange local buckling, AISC-F3.2:
!
λ − λpf
Mn = Mp − Mp − 0.7Fy Sx
λrf − λpf
0.7(50)(93)
9.47 − 9.15
= 446 − 446 −
12
24.1 − 9.15
= 442 ft-kips
Inelastic lateral torsional buckling controls! Calculate the design moment strength.
φb Mn = (0.90)(338) = 305 ft-kips
The W21×48 beam has sufficient strength. The following table shows the moment corrected
for the beam weight.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Section
Mu
φb Mn
ft-kips
ft-kips
W21×48
303
305†
W21×44
303
190‡
W18×46
303
204‡
W16×45
303
235†
W14×43
303
228†
† Inelastic lateral torsional buckling controls
‡
∗
bf
2tf
h
tw
OKAY?
9.47∗
7.22
5.01
6.23
7.54
53.6
53.6
44.6
41.1
37.4
OK
NG
NG
NG
NG
Elastic lateral torsional buckling controls
Flange local buckling limit state must be checked
(f) Check Case 1. The following table shows the moment corrected for the beam weight.
Section
Mu
φb Mn
ft-kips
ft-kips
bf
2tf
W21×48
394
398‡
9.47∗
‡
W21×44
393
311
7.22
W18×46
393
333‡
5.01
W16×45
393
309
6.23
W14×43
393
261
7.54
‡ Elastic lateral torsional buckling controls
∗ Flange local buckling limit state must be checked
h
tw
OKAY?
53.6
53.6
44.6
41.1
37.4
OK
NG
NG
NG
NG
Use W21×48 with Fy = 50 ksi steel.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
12.3. Determine the maximum service load W (kips) at the mid-height of the beamcolumn shown in the accompanying figure. Assume the member is hinged with respect to
bending in both x and y directions at the top and bottom. Additionally, lateral support
occurs in the weak direction at mid-height.
Use LRFD Design Method
(a) Obtain factored loads.
Pu = 1.2(100) + 1.6(150) = 360 kips
1
Mnt = Wu (22) = 5.5Wu
4
(b) Check the section type.
h
i h
i
q
h = 12.3 ≤ λ = 3.76 E = 90.6
p
Fy
htw
i
i h
q
bf
E
; 2tf = 4.96 ≤ λp = 0.38 F = 9.15
y
The web is compact and the flange is
compact.
(c) Column action with a compact web and flange, use AISC-E3 with Kx = Ky = 1.0;
Lx = 22 ft; Ly = 11 ft.
Find the maximum KL
r
K y Ly
K x Lx
1.0(22)(12)
1.0(11)(12)
= 47.3 ;
= 41.8
=
=
rx
5.58
ry
3.16
h
i h
i
q
KL
E
For r = 47.3 ≤ 4.71 F = 113
y
Fe =
π2E
π 2 (29, 000)
=
= 128 ksi
(KL/r)2
(47.3)2
h
i
h
i
Fcr = 0.658Fy /Fe Fy = 0.65850/128 (50) = 42.5 ksi
φc Pn = φc Fcr Ag = 0.90(42.5)(39.9) = 1, 520 kips
(d) Beam action with a compact web and flange, use AISC-F2 with Lb = 11 ft.
Use AISC-F1 to find Cb with Rm = 1.0 for doubly symmetric members.
12.5Mmax
Cb =
Rm ≤ 3.0
2.5Mmax + 3MA + 4MB + 3MC
12.5M
=
(1.0) = 1.67
2.5M + 3(0.25M ) + 4(0.50M ) + 3(0.75M )
For the limit state of yielding, AISC-F2.1:
Mn = Mp = Fy Zx = (50)(214)/12 = 892 ft-kips
For the limit state of lateral torsional buckling, AISC-F2.2:
From the AISC Manual Table 3-2 p. 3-16, Lp = 11.2 ft and Lr = 63.3 ft.
[Lb = 11 ft] ≤ Lp = 11.2 ft lateral torsional buckling does not apply, AISC-
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
F2.1(a).
Yielding controls! Calculate the design flexural strength.
φb Mn = (0.90)(892) = 802 ft-kips
(e) Moment magnification. Obtain the slenderness ratio for the axis of bending.
KL
K x Lx
= 47.3 (from above)
Axis of bending
=
r
rx
π 2 EI
π 2 (29, 000)(1240)
Pe1 =
=
= 5, 090 kips
(KL)2
[(1.0)(22)(12)]2
According to AISC-C1.1b, for transverse loading, Cm = 1.0.
Cm
1.0
B1 =
=
= 1.076
1 − Pu /Pe1
1 − 360/5, 090
(f) Use AISC-H1 to check the beam-column.
360
Pu
= 0.236 ≥ 0.2 so use AISC Formula (H1-1a) omitting the y-axis
=
φc Pn
1, 520
bending term.
Pu
8 Mux
8 (1.076)(5.5)Wu
= 0.236 +
≤ 1.0
+
φc Pn 9 φb Mnx
9
802
1.0 − 0.2362
Wu =
= 116.5 kips
0.006556
Calculate the service load.
1.2(0.2W ) + 1.6(0.8W ) = 116.5 kips
W = 76.7 kips
Service concentrated load is W = 76.7 kips.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
12.4. Investigate the adequacy of the given section of the accompanying figure. No joint
translation can occur and external lateral support is provided at the ends only.
Use LRFD Design Method
(a) Obtain the factored loads.
MaDL
MaLL
MbDL
MbLL
Mnta
Mntb
Pu
= McDL = 2.90 ft-kips
= McLL = 3.80 ft-kips
= 2.00 ft-kips
= 2.50 ft-kips
= 1.2(2.9) + 1.6(3.8) = 9.56 ft-kips
= 1.2(2) + 1.6(2.5) = 6.4 ft-kips
= 1.2(14) + 1.6(50) = 96.8 kips
(b) Column action:
KL
r
φc Fcr
φc Pn
Pu
φc Pn
Largest
(KL)y
1.0(15)12
=
= 111
ry
1.62
= 18.2 ksi
= φc Fcr Ag = 18.2(8.25) = 151 kips
96.8
=
= 0.643 > 0.2 Use AISC Formula (H1-1a)
151
=
(c) Beam Action. Neither lateral torsional buckling nor web local buckling are limit states
for weak axis bending. Check flange local buckling.
"
s
# "
#
bf
E
= 7.0 < λp = 0.38
= 9.15 ; section is compact.
2tf
Fy
1
φb Mn = φb Mp = φb Fy Zy = 0.9(50)(10.1) = 37.9 ft-kips
12
(d) Moment magnification. Obtain the slenderness ratio for the axis of bending. The beam
is bending about the weak axis.
KL
KL
Axis of bending
=
= 111
r
r y
π 2 (29, 000)(21.7)
π 2 EI
Pe1 =
=
= 191 kips
(KL)2
[(1.0)(15)(12)]2
Pu
96.8
Cm = 1 − 0.4
= 1 − 0.4
= 0.798
Pe1
191
Cm
0.798
B1 =
=
= 1.615
1 − Pu /Pe1
1 − 96.8/191
(e) Check AISC Formula (H1-1a), omitting the x-axis bending term.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.
Pu
8
+
φc Pn 9
Muy
φb Mny
96.8 8 1.615(9.56)
=
+
191
9
37.9
= 0.643 + 0.362 = 1.005 > 1.0 No good!
Section has insufficient strength for the given loading.
© 2010 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained from
the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical, photocopying,
recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle River, NJ 07458.