2°EMT- ITS

2°EMT- ITS
Conjuntos, Relaciones y Funciones
1.
1


Sea f  (3, 0), ( , 2), (5, 1), (0,5)  , determine:
2


i) D ( f ) .
ii) x / f (x) =5 e y / f (3)=y.
iii) Grafique f en ejes coordenados.
Sea g  (4, 2),(5, 2.5),(0,0),(6, 3),  3, 1.5 , determine:
2.
i) D ( g ) .
ii) Escriba una expresión genérica para g (x) .
iii) Grafique g.
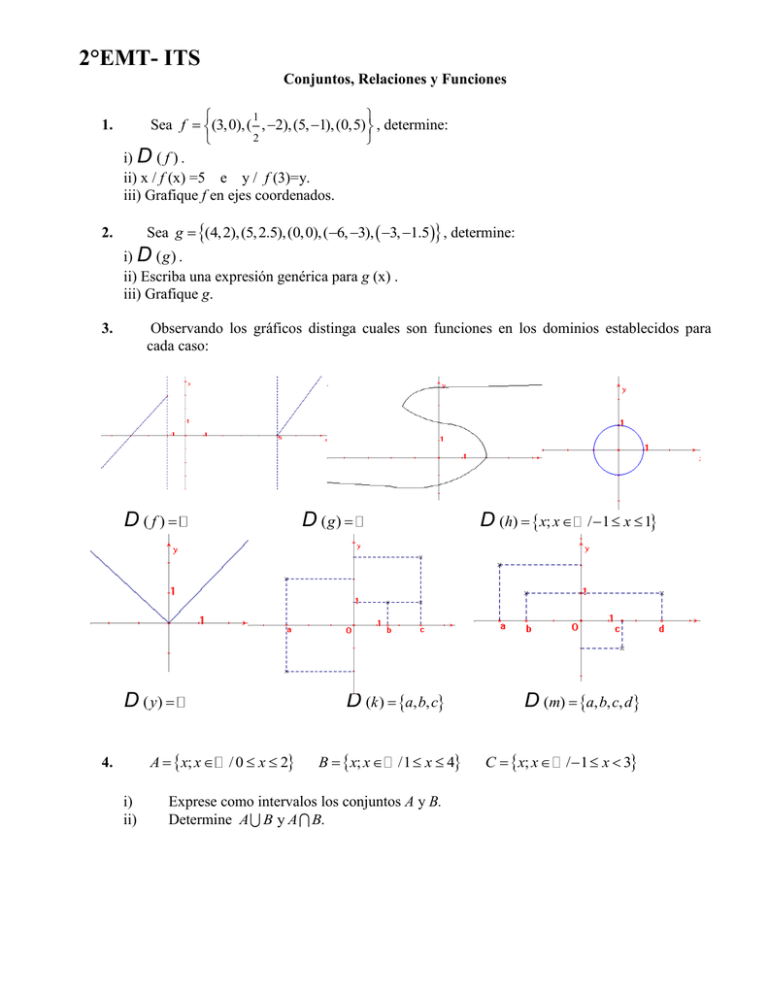
3.
Observando los gráficos distinga cuales son funciones en los dominios establecidos para
cada caso:
D (f)
D ( y) 
A  x; x  / 0  x  2
4.
i)
ii)
D (g) 
D (k )  a, b, c
B  x; x  /1  x  4
Exprese como intervalos los conjuntos A y B.
Determine A B y A B.
D (h)  x; x 
/  1  x  1
D (m)  a, b, c, d
C  x; x  /  1  x  3
2°EMT- ITS
x  3

; R  ( x, y) / y 

x 1 

Sea A  2, 1, 0,1, 2 , R : A 
5.
Determinar R por extensión.
¿R es función de A en ? Justificar.
i)
ii)



Sea A  4,5,10 , B  10,12 .R : A  B ; R  ( x, y) / x  y  ( y  x)
6.
Determinar R por extensión.
¿R es función de A en B ? Justificar.
i)
ii)
7. Sea A  2, 1, 0,1, 2 , B  5, 2, 4 .R : A  B ; R

x2  4 
 ( x, y) / y  2

x  2

Determinar R por extensión.
¿R es función de A en B ? Justificar.
Hay cuatro subconjuntos de R que son funciones biyectivas de codominio B.
Determínelas.
i)
ii)
iii)
3
1 1
3 3 1 1

8. Dados A   ,  , 1, 2, 0,   , B   ,  ,  , , 5,1 .
2
2 2
2 2 3 4

4x 1 
R : A  B ; R  ( x, y ) / y 

2x  3 

i)
Determinar R por extensión.
4x 1 

Hallar A para que f : A  B sea función biyectiva con f   x, y  ; y 

2x  3 

ii)
9. Sean A   ;  /  3    3 , B   ;   /  2    6 .
R
i)
ii)
: A  B ; R  ( ,  );   2  4 si   0 ,   2  1 si   0
Hallar R por extensión.
Clasificarla.
10.
a) A partir de los siguientes datos de la función f :
sgn f
+
+
-3
-1
+
3
 , esboce un gráfico.
crec.f
x
-3
-2
2
x
2°EMT- ITS
Corte con Oy (0,-1)
b) Resuelva f(x)<0.
11. A) Observando el gráfico de la función f:
D (f) =………….
i.
D(f)

, completar:
raíces:…..……..
Signo de f…………………………….
ii.
R (f) =……..
iii.
Máx. abs:………. Mín. abs:.……….
Max relativos:…………………..
Mín. relativos:………………….
crecimiento de f………………………
Función Lineal y Cuadrática
12.
Dadas las siguientes funciones definidas en R : a) estudia raíz, ordenada en el origen, sig.de
f(x) , crecimiento, decrecimiento y grafica.
a) f : f (x)=2x-6
b) f : f(x)=3(x+2)
c)
f : f(x)= -
1
x4
2
En cada caso, justifica crecimiento-decrecimiento, según i) coeficiente principal, ii)
definición.
13. Dada
j:
la

función
h:
 ; h( x)  2 x  4
y
,dada por el gráfico:
a) Grafique las dos funciones en un mismo sistema
de ejes cartesianos.
b) Hallar el correspondiente de x según j (la fórmula
de j).
c) Encontrar gráficamente y analíticamente
gr (h) gr ( j ) .
d) Resolver en R j(x)>h(x).
2°EMT- ITS
14. Sea p, una función lineal de la cual se sabe que su corte con Oy es (0,-6) y el ángulo que forma
su gráfico con el eje Ox es de 71,5 grados:
a) Hallar p(x)
b) Hallar el signo de p(x).
15. En la primera fila aparecen tres gráficos de funciones cuadráticas y a continuación una lista de
funciones: Determinar que función le corresponde a cada gráfico.
1)
2)
3)
1
1
1
j(x)=- x 2  2 ; k( x)  ( x  2)2 ; l(x)=- x 2  2 ; m( x)  ( x  2)2 ; p(x)= x 2  2
2
2
2
2
q( x)  3( x  2)( x  1) ; r( x)  ( x  2) ; s( x)  3( x  2)( x  1) ; t( x)  3( x  2)( x  1)
16.
Resolver las siguientes ecuaciones en
:
1) 9 x  30 x  25  (3x  5)(2 x  1)
2
17.
Dada la función f :
18.
Sea g :

;
2) ( x  1)(2 x2  x  3)  x2 -1
 ; f ( x)  2 x2  4 x  6 , realizar E.A. y R.G.
dada por el siguiente gráfico:
a) Hallar el correspondiente de x según g (la fórmula)
b) Considere la función f del ejercicio anterior, hallar el
punto de corte del gráfico de f con el gráfico de g.
c) Resolver en R; f(x) > g(x)
2°EMT- ITS
19.
20.
En el partido Uruguay-Venezuela, el PICHICHI uruguayo efectuó un tiro-libre cuya
x2
trayectoria se corresponde con el gráfico de la función f ( x)  
 2 x , la barrera se
10
encuentra a 10m:
a) Cuanto tiene que medir el hombre de la barrera para detener el tiro-libre.
b) Determinar a qué distancia debe estar el arco para que sea GOL si el arco mide 2,5m.
Los organizadores de un recital encargarán la construcción de un escenario rectangular, que
tendrá una franja de 2 m de ancho en todo su contorno. Toda la superficie, incluida la franja,
estará cercada por una valla de seguridad. Los artistas solicitaron que el escenario tenga un
área de 240 m2, y los encargados de seguridad requieren que el largo del rectángulo sea el
doble de su ancho.
Calcula la longitud que deberá tener la valla de seguridad.
Función Exponencial y Logarítmica
21.
Matías recibió un sms donde aparecía lo siguiente: “Si reenvías este mensaje a 3
personas en la siguiente hora, tendrás 24 horas de buena suerte; si se lo envías a 5
personas tendrás una semana de buena suerte…”:
a) Completa la siguiente tabla, suponiendo que todos los que recibieron el mensaje,
decidieron tener un día de buena suerte.
1h
2 hs
3hs
…..
Mensajes
enviados
Representa la información gráficamente.
….
1día
t hs
b) Completa la siguiente tabla, suponiendo que todos los que recibieron el mensaje,
decidieron tener una semana de buena suerte.
1h
2 hs
3hs
…..
1día
….
t hs
Mensajes
enviados
Representa la información gráficamente.
c) Si todos envían el mensaje a 5 personas, en cuanto tiempo las empresas de telefonía
móvil recaudan aproximadamente u$s12.000.000 .
22.
Completar las siguientes tablas
a) Representar los resultados en sendos sistemas
de coordenadas cartesianos. ¿Qué observa?
b) De acuerdo a los gráficos realizados, escribe el
dominio, el recorrido, el signo y el crecimiento
de cada una de las funciones.
x
1
2
3
10
100
-1
-2
-10
-100
x
1
2
3
10
100
-1
-2
-10
-100
2°EMT- ITS
23.
Resolver en (,,·, ) :
i)
3 x  9 2 x 3
ii)
5 3x  2 
iv) 3  2. 3  3  0
2x
x
25.
26.
iii) 3
2x
x
v) 10  10  2  0
2 x 1
1 0
viii) e
2 x 1
4
vii) 4
24.
1
0
25
2x
x
vi) e  3.e  2  0
x
x
x) 4  6.2  8  0
Las sustancias radiactivas se desintegran con el paso del tiempo. La cantidad de una cierta
sustancia radiactiva que va quedando al pasar un tiempo t viene dada por: M  M 0 .a t con M 0
la cantidad de sustancia inicial y a una constante (0  a  1) que depende de la sustancia en
cuestión y de la unidad de tiempo que tomemos.
Sabiendo que el período de semi-desintegración del radio es de 1620 años (período de tiempo
en el cual su masa inicial se reduce a la mitad) y partiendo de una muestra de 1 gramo de
radio en el año 1900:
i)
¿Qué cantidad de radio quedará en el año 2000? ¿Y en el 3000?
ii)
¿Cuándo quedará 0,8 g de radio? ¿Cuando había 1,5 g de radio? ¿En algún momento
la sustancia desaparece completamente?
Calcular: i)log 2 8 ii)log10 1000000 iii)log 4 2 iv)log b 1 v)log a a vi)log b b 
Completar las siguientes tablas
x
1
2
3
10
100
1/2
1/4
1/10
1/100
x
1
2
3
10
100
1/2
1/4
1/10
1/100
log2x
log1/2x
Considera las siguientes funciones: f: f(x)= 5.3x y g: g(x)= log (x+1) cuyos dominios son
(f)= ℝ y
(g) = (-1,+∞)
a) Calcula si es posible :
i) f(0)
ii) g(0) iii) f(-3)
iv) g(-3)
b) Indica cuando sea posible , para qué valor aproximado de x se cumple que:
i) f(x)=8
ii) g(x)=5 iii) f(x)=0
iv) g(x)=0
D
28.
 243
2 x 3
e0
ix) e
c) Representar los resultados en sendos
sistemas de coordenadas cartesianos.
¿Qué observa?
d) De acuerdo a los gráficos realizados,
escribe el dominio, el recorrido, el
signo y el crecimiento de cada una de
las funciones.
27.
x
D
Resolver en (,,·, ) :
(
)
i)
iii)
(
)
(
v)
√
vii)
√
ii)
)
iv)
vi)
(
)
viii)
(
iii) (
)
(
)
)
2°EMT- ITS
Función Racional
29.
El siguiente es un bosquejo de g: D ( g )  / g ( x) 
ax  b
, determinar:
cx  d
i)D ( g )
ii) Raíces de g
iii) Signo de g
iv) Asíntotas
v) Corte con Oy
vi) Signo de g(-9)
30.
Dada la función f: D ( f ) 
/ f ( x) 
x2
12  6 x
a) E.A y R.G. de f(x.)
b) Resolver: f ( x)  0
c) Sea g :
 ; g ( x) 
5  2x
, hallar gráficamente y analíticamente gr ( f ) gr ( g ) .
6
d) Resolver gráficamente f(x)>g(x).
31.
Hallar el dominio y las raíces de las siguientes funciones:
x2  4
12
3
b
(
x
)

2
x

1

a ( x) 

x 1
( x  4)2 ( x  4)
x 1
x
32.
Resolver en R: i )

5  x x 1
x
1
2 0
ii )
x4
x2
x 1 x  4
iii )


6  3x 2  x 6  3x
2°EMT- ITS
Función Cuadrática ( con derivada)
33.
Estudio analítico ( EA ):
Dominio. Ceros. Signo. Ordenada en el Origen. Calculo de “Función Asociada”. Máximos y
mínimos. Ramas Infinitas
Representación gráfica (RG).
f1(x) = x2 -5x + 6
f2(x) = x2 – 1
f4(x) = (x-5) (x+3) f5(x) = (x -2)2
f7(x) = ½ x2
f8(x) = -x2 + x – 1
f10(x) = (x-1)(x+2)-2(x-1)
34.
f3(x) = -2x2 – 4
f6(x) = -2x2 - 3x
f9(x) = 3x2 - x
Sea la función g / g ( x)  2 x 2  bx  c
a) halla b y c reales / g(1)=-12 y g( 3)=0
b) para b y c hallados EA y RG de g(x).
35.
Sea g:ℝ→ℝ dada por el siguiente gráfico:
a)
b)
c)
36.
Hallar el correspondiente de x según g (la fórmula).
Dada la función f:R→R; f(x)=-2x+7 hallar el punto de corte
del gráfico de f con el gráfico de g.
Resolver en R; f(x) > g(x)
Resolver las siguientes Inecuaciones:
(x - 3)2 - (2x - 5)2 ≤ 0
2x + ½ < 0
2x2 ≤ 1 - 12x+11
2
2x2 -1 - x2 -1 ≥ 12x + 3 – 2x
3
2
6
-3x + 15 ≤ 0
-x2/3 ≥ x-8
(4x2 - 8x) . (1- 2x) ≤ 0
Polinomios (Identidad, Operaciones elementales, Ruffini, teroema del resto, Descartes y
descomposición factorial)
Función Polinómica de tercer grado
2°EMT- ITS
37.
Estudio analítico ( EA ):
Dominio. Ceros. Signo. Ordenada en el Origen. Calculo de “Función Asociada”. Máximos y
mínimos. Ramas Infinitas
y Representación gráfica (RG).
h1(x) = (x-2) (x-1) 2
h2(x) = x . (x2 -8/3 x -1)
h3(x) = (x – 1)2 ( x + ½)
h4(x) = (x-3)3
h5(x) = (x+3)(x–4)( x + 2)
h6(x)= -2(x-2) 2(x+1)
h7(x)= -x ( x2 -2x + 3)
3
2
h8(x)= -x +2x +5x+1
38.
39.
Dado P(x) = 2 x 3  a  1x 2  3a  bx  2a  3b hallar a y b sabiendo que P(x) dividido
entre (x-2) da resto 2 y que P(x) dividido entre (3x+3) da resto 5.
Sea el polinomio P(x) = 2x3 + ax 2 -10x + b
i)Hallar a y b sabiendo que P(x) es divisible entre (x+3) y que P(x) dividido entre ( x+2) da
resto 8.
ii)Con a y b hallados expresar P(x) descompuesto factorialmente, estudiar signo y bosquejar.
iii) halla cociente y resto de dividir ( P( x) entre (2 x 2  x  2)
40.
3
2
Sea P(x) = x  5 x  2 x  8 cuyo signo es:
Se pide calcular los extremos relativos.
41.
Dada la función polinómica f: f(x) = 2x3 + ax2 -23x + b+2 ,
i)
hallar a y b sabiendo que f(x) dividido (x – 2) da resto -30 y que 3 es raíz,
ii)
escribe la descomposición factorial de f(x).
iii)
Resuelve f(x) >0
42.
a) Estudia signo de la función g: g(x) = (-x+ 1) (x2 -16).
b) Realiza su bosquejo.
c) Desarrolla y halla sus extremos relativos.
43.
Sea F(x) = 2x 3+ (a - b) x2+ ax + 2b
 Determinar el polinomio F(x) en su forma general sabiendo que:
F(3) + F(1) = 120 y que F(x) es divisible entre (x+2)
 Escribir la descomposición factorial de F(x)
2°EMT- ITS

44.
45.
46.
Calcular Q(x) sabiendo que Q(x) = F(x) + (2x - 1)2
Dado P(x)= x3-3x2+ax+3 i) hallar a sabiendo que P(x) es divisible entre (x-1).
Dado P(x)= -2x3+6x2+ax+b
i) hallar a y b sabiendo que P(x) es divisible entre (x+2) y que dividido entre (x-1) da resto
–12.
ii)para a y b hallados estudiar signo de la imágenes de P(x) , efectuar DF y bosquejar.
iv)
resolver P(x)<0
El sig. gráfico corresponde a una función real de tercer grado
a. halla la expresión de f(x)
b. indicar el signo de f(x)
c. indicar el signo de f’(x)
47.
Observando el gráfico adjunto halla f(x) sabiendo que es una función de segundo grado y
que el coeficiente principal es 3 ,
¿ es f (x) divisible entre ( x + 2)?
¿ y entre x?
48.
a. Determinar f(x) a partir de su gráfico sabiendo que es de tercer grado.
b. Estudiar sg. de f (x).
c. ¿ De qué signo son f ( 5/2) , f( -1/4) y f ( 563)?
d. Determinar el resto de dividir f (x) entre : i) ( x + 3 ) ; ii) x .
e. Resuelve f(x)≤ 0
2°EMT- ITS
49.
Dado el gráfico de la función polinómica f de tercer grado : a) hallar la expresión f(x)
sabiendo que f(2) = 20. b) Estudia sg. f(x). c) Resuelve f(x) > 0 .
50.
Escribir la descomposición factorial de las siguientes funciones polinómicas :
A(x) =2x3 - x2 - 7 x + 6 ; B(x)=2x3 - 7 x2 - 7 x + 12 ;
C(x) = x3 + 5 x2 - 8 x – 12; D (x) =2 x3 + 9x2 + 10 x + 3 ;
E(x) = -7x4 + 12 x2 + 2 x5 - 7x3 ; F(x) =2x4 - x3 -7x2 +6x
Funciones definidas por intervalos – Continuidad – Lectura de gráficos
51.
Representar gráficamente las siguientes funciones
x–1
1.
2.
–1
si x < 1
4–x
si x ≥ 1
3
si x < 1
3. f(x) =
3
si x ≥ 2
x–1
si x ≤ 3
f(x) =
4. f(x) =
2
52.
si x < 2
f(x) =
4–x
si x > 3
si x ≥ 1
 x 2  1 si x  1
investiga continuidad en x=1 y bosqueja.
2x
si x  1
a) Sea g:g(x)= 

 x 2  2x  1 si x  0

si x  0
2x - 1
b) Idem. en x=0 si f:f(x)= 
53.
2 x  1 si x  2
a) Sea g : g(x) = 
representa gráficamente e indica ceros y signo.
2
9
x
si
x

2

b) Investiga continuidad en x=2. Justifica.
c) Observando el grafico indica lim para x   .
5  x si x  3
d) Sea g : g(x) =  2
representa gráficamente e indica ceros y signo, investiga
x  9 si x  3
continuidad en x=3 Justifica .
Observando el grafico indica lim para x   .
2°EMT- ITS
54.
El siguiente gráfico corresponde a una función real , indica:
a)
b)
c)
d)
55.
dominio y recorrido
ceros y signo
crecimiento y extremos relativos
lim f(x)
lim f(x)
lim f(x)
+
x→ 2
x→ 2
x→ +∞
lim f(x)
x→ - ∞
Observa el gráfico adjunto correspondiente a una función f, e indica:
a) Dominio de f;
b) raíces y signo de f(x);
c) crecimiento, decrecimiento y extremos (relativos absolutos);
d) lim f(x)
lim f(x)
x
+∞
x
+∞
e) lim f(x)
lim f(x)
lim f(x)
lim f(x)
x
0+
x 0x
7+
x
7–
56.
PROPUESTAS DE PARCIALES
Primer parcial Matemática 2°EMT turno Matutino
2°EMT- ITS
23 de junio 2014
EJERCICIO 1
Observando El gráfico de la función
( ) ℝ ℝ completar:
( )
i)
ii) signo de f(x)
iii) Extremos
iv) crecimiento
EJERCICIO 2
Sea ( )
a) Hallar
ℝ, sabiendo que
( )
.
b) Hallar todas las raíces de ( ).
( ).
c) Hallar
EJERCICIO 3
A partir de los siguientes datos de la función f, esboce un posible gráfico de ella.
Signo de f (x) -
0
-5
+ 0
-3
-
- 0 + 0
-2
-1
4
- 0 +
6
x
im 𝑓(𝑥)
∞
im 𝑓(𝑥)
∞
im 𝑓(𝑥)
∞
im 𝑓(𝑥)
∞
𝑥 − +
𝑥 − −
Crec. f
( )
M
-4
-2
(
)
M
2
m
5
( )
𝑥 +∞
x
𝑥 −∞
( )
EJERCICIO 4
Dados los conjuntos A={0,1,2,3,4} y B={-2,-1,0,1,2,3}
a) Hallar por extensión una relación de A→B y una de B→A.
b) Sea f: A→B/f(x)=x+a, determinar un valor de a ℝ sabiendo que f es función. Clasificar f en
sobreyectiva, inyectiva o biyectiva.
c) Hallar por extensión A’, sabiendo que A
y que f: A’→B es función biyectiva, siendo f la
función definida en la parte b.
2°EMT- ITS
2°EMT- ITS
2°EMT- ITS
2°EMT- ITS
2°EMT- ITS
2°EMT- ITS
Examen de Matemática- 7 de julio de 2014
Nombre:
1)
Grupo:
Se da la función racional
( )
a)
b)
c)
d)
e)
f)
Estudia el dominio de q explicando como lo razonas.
Determina la raíz, y la ordenada en el origen de q
Calcula f(7) , f(-3) y f(-2)
Estudia el signo de las imágenes de f
Hallar las ecuaciones de las asíntotas.
Representar gráficamente
2)
La siguiente es la representación gráfica de la función f(x)=log (x)
a)
Determina siempre que sea posible:
f(-1), f(1), f(x)=3
b)
Representa gráficamente en el mismo sistema de ejes coordenados
(explicando como lo realizas) la función
g : g(x)=log(x+2) , y la función h: h(x)=log(x)+2.
c)
Indica dominio de g y de h.
d)
Halla raíz, ordenada en el origen de g. Explica como lo hiciste.
3)
Dado ( )
a) Hallar
a yb
(
sabiendo que
)
P x
es divisible entre (x+1) y que P(2)=-75
b) Escribe la descomposición factorial de
P( x) .
c) Hallar cociente y resto de dividir P(x) entre
d) (LIBRES) EA y RG del polinomio P(x)
4)
( )
-1
Resuelve en R:
a.
b.
c.
d.
+
(
(
+
)
)
(
)
(
)
2°EMT- ITS
Ejercicios de exámenes
q : q ( x) 
1) Se da la función racional
g)
h)
i)
j)
k)
l)
x7
2 x  8
Estudia el dominio de q explicando como lo razonas.
Determina la raíz, y la ordenada en el origen de q
Calcula q(10) , q(-6) y q(-12)
Estudia el signo de las imágenes de q
Hallar las ecuaciones de las asíntotas.
Representar graficamente
5) La siguiente es la representación gráfica de la función f(x)=2x
e) Determina:
f(-1), f(3), f(x)=8 , f(x)=1
f) Representa gráficamente en el mismo sistema de ejes coordenados (explicando como
lo realizas) la función
g : g(x)=2x -1 , y la función h: h(x)= 2x - 2.
g) Indica recorrido de f y de h
h) Halla raíz, ordenada en el origen de h. Explica como lo hiciste.
6) Dado
P  x   3x3  ax2  bx  36
a) Hallar a y b sabiendo que
P x
es divisible entre
b) Escribe la descomposición factorial de P( x) .
 x  3 y que 1 es raíz P  x  .
2°EMT- ITS
c) Determina el polinomio
Q x
sabiendo que
P  x   Q( x).T ( x)
y que
T  x  x 1
7) Dada la representación gráfica de un polinomio de tercer grado Q( x) :
a. Escribe la descomposición factorial de Q( x)
b. Escribe la expresión desarrollada de la función.
c. Realiza diagrama del signo de Q( x) .
I.
Resuelve en R:
2) log5  x  3  2
3
4) 2 .2  26
3) 27
x
x1
2x
5) 4  3.4  2.4  32
x
x
x
8) A) Indica si los siguientes gráficos corresponden a funciones, indicando su dominio y recorrido:
B) Se definen: A={xϵℕ*/ x<5} y B={ -1,0,1,2}. Dada las siguientes relaciones:
g: A →B/ g={ (x,y) / x=y2} y h: A→B/ h={(x,y)/y=x-2}
a. ¿Son g y h una función? En caso afirmativo clasificarla. Justifica tu respuesta.
b. Es posible definir una función de A en B que sea inyectiva pero no sobreyectiva, justifique.