Parcial III – Cálculo Vectorial

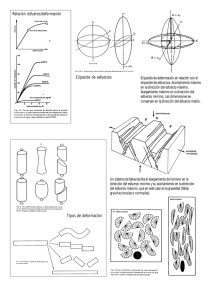
Parcial III – Cálculo Vectorial
Octubre 26 de 2010
Resuelva completamente el punto I y uno entre el II y el III
(12 Puntos) I. El elipsoide 4x2 +4y 2 +z 2 = 4 encierra parte de la esfera x2 +y 2 +z 2 = 2z.
(i) Haga una gráfica de ambas superficies, encuentre y grafique su curva de intersección.
(ii) Encuentre el área de la superficie de la esfera que queda encerrada por el elipsoide.
(iii) Encuentre el volumen de la región interior tanto al elipsoide como a la esfera.
(4 Puntos) II. Sea D el disco de radio 2 centrado en el origen. Calcule la siguiente
integral:
ZZ
sen (x2 + y 2 ) dA.
D
Haga una gráfica del volumen que calcula tal integral.
(4 Puntos) III. Haga una gráfica del sólido cuyo volumen está dado por la integral
Z
1
Z
3−y
Z
1−y 2
dz dx dy.
0
1−y
0
Calcule el volumen correspondiente.
Solución
I.
(i) El elipsoide 4x2 + 4y 2 + z 2 = 4 está centrado, mientras la esfera tiene radio 1 y centro
en (0, 0, 1) ya que x2 + y 2 + z 2 − 2z = 0 ⇔ x2 + y 2 + (z − 1)2 = 1. Para encontrar la
curva de intersección de estas dos superficies podemos despejar x2 + y 2 = 1 − (z − 1)2
en la ecuación de la esfera y reemplazarlo en la del paraboloide:
4(x2 + y 2 ) + z 2 = 4 − 4(z − 1)2 + z 2 = 4 − 3z 2 + 8z − 4 = 4,
es decir 3z 2 − 8z + 4 = 0, ası́ que los valores para z están dados por las dos soluciones
a esta ecuación cuadrática:
√
8 ± 64 − 48
8±4
z=
=
,
6
6
es decir z = 2 y z = 32 . Si z = 2 en ambas ecuaciones, la de la esfera y la del
elipsoide, tenemos que x2 + y 2 = 0, luego el punto de corte es (0, 0, 2), mientras
que, si z = 23 , en ambas ecuaciones tenemos que x2 + y 2 = 89 , ası́ que a esta altura
√
la curva de intersección es un cı́rculo de radio 38 , como lo ilustra la siguiente figura:
(ii) Para encontrar el área de la superficie de la esfera x2 + y 2 + (z − 1)2 = 1 que queda
encerrada por el elipsoide despejamos la coordenada z en la ecuación y calculamos la
integral
s
2 2
ZZ
∂z
∂z
A(S) =
+
dA,
1+
∂x
∂y
D
√
donde D es el disco de radio 38 , de acuerdo con lo hayado en el punto anterior. Como
p
z = 1 ± 1 − x2 − y 2 , y la raiz negativa corresponde al hemisferio sur de la esfera (el
que queda encerrado por el elipsoide)
ZZ r
1
A(S) =
dA,
2 − y2
1
−
x
D
√
que, en coordenadas polares, con 0 ≤ θ ≤ 2π y 0 ≤ r ≤
√
8
3 ,
√
Z 38
1
1
√
√
A(S) =
r dr dθ = 2π
r dr
2
1−r
1 − r2
0
0
0
√
h p
i 38
1
4π
= 2π − 1 − r2
= 2π 1 −
=
.
3
3
0
Z
2π
Z
8
3
queda
2
(iii) La
RRRregión interior tanto al elipsoide como a la esfera tiene un volumen igual a V (E) =
dV que, en coordenadas cilı́ndricas, puede parametrizarse sobre el disco D usado
E
anteriormente como
Z √8 Z √
Z
2
2
2π
4−4x −4y
3
V (E) =
√
0
0
1−
dV,
1−x2 −y 2
donde los lı́mites inferior y superior en la altura z están dados por las ecuaciones de
la parte superior del elipsoide y la parte inferir de la esfera, respectivamente. Ası́,
Z 2π Z √38 Z √4−4r2
Z 2π Z √38 p
p
2 − (1 −
V (E) =
r
dr
dθ
=
4
−
4r
1 − r2 ) r dr dθ
√
0
1− 1−r 2
0
0
0
√
2π
Z
Z
=
0
8
3
√
0
3
(1 − r2 ) 2
6π −
3
8
3
#
0
√
Z
p
1 − r2 r dr − 2π
0
√
"
=
8
3
Z
h p
i
3 1 − r2 − 1 r dr dθ = 6π
8
3
r dr
0
√
r2
− 2π
2
8
3
0
1
1
8π
28π
= 6π
−
−
=
.
3 81
9
27
RR
II. La integral D sen (x2 + y 2 ) dA, donde D el disco de radio 2 centrado en el origen
puede calcularse mediante coordenadas polares:
ZZ
Z 2π Z 2
cos r2 2
2
2
sen (x + y ) dA =
sen (r2 ) rdrdθ = 2π[−
] = π[1 − cos 4].
2 0
D
0
0
III. Para encontrar la gráfica del sólido cuyo volumen está dado por la integral
Z 1 Z 3−y Z 1−y2
dz dx dy.
0
1−y
0
veamos primero que los lı́mites en cada variable dados son:
0 ≤ y ≤ 1,
1 − y ≤ x ≤ 3 − y,
0 ≤ z ≤ 1 − y2 .
Ası́, para lı́mites constantes en y tenemos que la variable x se encuentra acotada entre dos
rectas, mientras z está entre cero y un cilı́ndro parabólico. La gráfica es la siguiente:
Z
0
Finalmente, sin necesidad de hacer cambios de variable podemos calcular
Z 1 Z 3−y
Z 1
Z 3−y Z 1−y2
dz dx dy =
(1 − y 2 ) dx dy =
(1 − y 2 )[(3 − y) − (1 − y)] dy
1
1−y
0
0
1−y
Z
=
2
0
1
3
(1 − y 2 ) dy = 2[y −
0
3
y 1
4
] = .
3 0
3