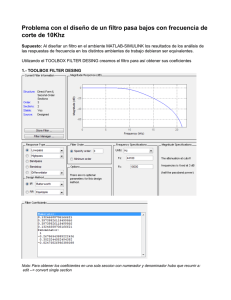
1 Práctica Nº 1 Control Clásico Matlab 7 Agosto 2012

U
UN
NIIV
VE
ER
RSSIID
DA
AD
DA
AU
UT
TÓ
ÓN
NO
OM
MA
AD
DE
EN
NU
UE
EV
VO
OL
LE
EÓ
ÓN
N
F
FA
AC
CU
UL
LT
TA
AD
DD
DE
E IIN
NG
GE
EN
NIIE
ER
RÍÍA
AM
ME
EC
CÁ
ÁN
NIIC
CA
AY
YE
EL
LÉ
ÉC
CT
TR
RIIC
CA
A
D
DE
EP
PA
AR
RT
TA
AM
ME
EN
NT
TO
OD
DE
EC
CO
ON
NT
TR
RO
OL
L
Práctica N° 1 Laboratorio de Control Clásico
Aprendamos MatLab y Simulink
La práctica uno de Control Clásico, aunque esta dividida en dos partes, se realizará en
una sola sesión. El reporte será uno solo para las dos partes
OBJETIVO
Familiarizarse con el modo de operación de MATLAB y SIMULINK conociendo los comandos
principales que permitan obtener un mejor provecho al manejar el mismo.
SESIÓN SIMPLE DE MATLAB
Para arrancar Matlab oprima dos veces sobre el icono del escritorio de Windows
O bien, por el menú inicio
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
Laboratorio De Control Clásico
Al arrancar Matlab se observará la siguiente pantalla
COMANDOS Y EXPRESIONES
Los comandos y las expresiones se teclean en matlab como se muestra en la siguiente figura. El
resultado de una expresión se almacena automáticamente en la variable ans y se despliega con cuatro
cifras decimales por default.
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
2
Practica 1 Aprendamos MatLab y Simulink
VARIABLES
Matlab reconoce la diferencia entre minúsculas y mayúsculas, así volts, Volts y VOLTS son tres
variables diferentes. Las variables deben empezar con letra y no deben contener signos de puntuación
puesto que estos tienen otro significado en Matlab.
Nótese en la figura anterior como la definición de las variables voltaje y corriente van seguidas por
punto y coma (;), no así la declaración de la expresión para la potencia. Para Matlab, todo lo que
termina en punto y coma el resultado no se muestra en la pantalla. Puede usarse también la coma (,)
como separador de variables, pero el resultado se mostrará en la pantalla.
EL ESPACIO DE TRABAJO DE MATLAB (WORKSPACE)
Matlab mantiene el valor de todas las variables utilizadas, para saber que valor tiene una variable solo
teclee la variable y ENTER. Por ejemplo, para verificar el valor de las variables ans y voltaje, dadas
anteriormente
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
3
Laboratorio De Control Clásico
Nota: Los valores mostrados pueden cambiar en función de los valores que se hayan tecleado
Si no se recuerdan las variables utilizadas puede usarse el comando who, que nos muestra todas las
variables que hasta ahora se han usado.
SALVANDO Y RECUPERANDO DATOS
En adición a mantener el valor de las variables, Matlab puede almacenar como archivo todas las
variables usadas y recuperarlas posteriormente para otra sesión. Para guardar las variables se usa el
comando Save Workspace As del menú File.
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
4
Practica 1 Aprendamos MatLab y Simulink
Esto abre el siguiente cuadro de diálogo para teclear el nombre del archivo en el que se guardarán los
datos.
Para borrar todas o una de las variables almacenadas se usa el comando clear. Clear o clear all borra
todas las variables, se requiere espacial cuidado con este comando, ya que no podrán recuperarse. Para
borrar una o más variables el comando clear va seguido del nombre de la variable o variables. El
siguiente ejemplo borra las variables ans y pot
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
5
Laboratorio De Control Clásico
Nótese que los comandos de matlab deben teclearse en minúsculas, de no hacerse así, se mandará un
mensaje de error.
Para borrar todas las variables, se usa clear o clear all.
Note que el comando who nos muestra que no hay ninguna variable almacenada. Para recuperar las
variables se usa el comando Open, del menú File
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
6
Practica 1 Aprendamos MatLab y Simulink
Esto abre el cuadro de diálogo para teclear el nombre del archivo donde se almacenaron los datos
(datos.mat)
Puede verificar que las variables se hayan recuperado usando el comando who.
Otros comandos de matlab que puede probar son: whos, clc, help.
FUNCIONES
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
7
Laboratorio De Control Clásico
Las funciones de matlab son muchas, pero consideraremos aquí solo las básicas como: abs(), sin(),
asin(), angle(), exp(), log(x), log10(), sqrt() e imag().
Valor absoluto de un número
» a = 2 + j * 3; b = -4;
» abs(a)
ans =
3.6056
Función Seno y seno inverso (El ángulo debe estar en radianes)
» f = sin(pi/3), fi = asin(f)*180/pi
f=
0.8660
fi =
60.0000
Ángulo de un número
» teta = 180*angle(a)/pi
teta =
56.3099
Exponencial de un número
» exp(-2)
ans =
0.1353
Logaritmo natural
» log(ans)
ans =
-2
Logaritmo base 10
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
8
Practica 1 Aprendamos MatLab y Simulink
» log10(100)
ans =
2
Raíz cuadrada
» sqrt(875)
ans =
29.5804
Obtención de la parte imaginaria de un número complejo
» imag(a)
ans =
3
Otras funciones son cos(), acos, tan(), atan(), real(), conj()
ARREGLOS SIMPLES (VECTORES)
Los vectores en matlab se definen por medio de paréntesis rectangulares, ejemplo
» a = [1 3 0.8 4 6], b = [2+i 0.4-3*j 1 0 5]'
a=
1.0000
3.0000
0.8000
4.0000
6.0000
b=
2.0000 - 1.0000i
0.4000 + 3.0000i
1.0000
0
5.0000
Note que para definir un vector columna se utiliza el operador de traspuesta (‘, comilla). Otra forma
de hacerlo es separar cada elemento del vector por punto y coma (;).
Para direccionar los elementos del vector, segundo y cuarto elemento de a, por ejemplo:
» a(2), a(4)
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
9
Laboratorio De Control Clásico
ans =
3
ans =
4
Para el tercer y primer elemento del vector b
» b(3), b(1)
ans =
1
ans =
2.0000 - 1.0000i
La operación entre vectores obedece las reglas del álgebra de vectores, ejemplos
» c = a + b'
c=
Columns 1 through 4
3.0000 + 1.0000i 3.4000 - 3.0000i 1.8000
4.0000
Column 5
11.0000
»d=a*b
d=
34.0000 + 8.0000i
Otra forma de generar vectores de una forma simple es, por ejemplo:
t = (0:0.1:2) * pi, el cual nos genera el vector t cuyos elementos comienzan en 0, tiene incrementos de
0.1 hasta llegar al 2, todos multiplicados por 3.1416, es decir:
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
10
Practica 1 Aprendamos MatLab y Simulink
» t = (0:0.1:2)*pi
t=
Columns 1 through 7
0
0.3142
0.6283
0.9425
1.2566
1.5708
1.8850
Columns 8 through 14
2.1991
2.5133
2.8274
3.1416
3.4558
3.7699
4.0841
5.3407
5.6549
5.9690
6.2832
Columns 15 through 21
4.3982
4.7124
5.0265
GRÁFICOS SIMPLES
Con el vector t definido anteriormente se puede obtener la función senoidal dada por
y = sin(t);
que se puede graficar con el comando plot
» plot(t, y)
» grid
» title('Función senoidal')
» xlabel('tiempo'), ylabel('Seno(t)')
los comandos anteriores nos dan la siguiente gráfica
MATRICES
La forma de definir matrices en matlab es parecida a la de vectores; cada elemento de una fila está
separado ya sea por espacio o bien por coma, un renglón se determina por un punto y coma al final del
mismo, por ejemplo
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
11
Laboratorio De Control Clásico
» A = [ 1 0 2; 2 -1 3; 3 5 4]
A=
1
2
3
0
-1
5
2
3
4
La transpuesta de esta matriz esta dada por:
» B = A'
B=
1 2 3
0 -1 5
2 3 4
También, las matrices obedecen las leyes del álgebra de matrices, la resta de las matrices anteriores es
»C=A-B
C=
0
2
1
-2 -1
0 -2
2 0
El producto de éstas matrices es
»D=A*B
D=
5 8 11
8 14 13
11 13 50
La inversa de la matriz A es
» inv(A)
ans =
-2.7143 1.4286 0.2857
0.1429 -0.2857 0.1429
1.8571 -0.7143 -0.1429
MATRICES ESPECIALES
Matriz identidad o unitaria
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
12
Practica 1 Aprendamos MatLab y Simulink
» eye(3)
ans =
1 0 0
0 1 0
0 0 1
Matriz cero
» zeros(4)
ans =
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Matriz de unos
» ones(3, 5)
ans =
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Enseguida se presenta la Tabla 1 en la que se presentan las ordenes y funciones matriciales que se usan
en la resolución de problemas de control.
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
13
Laboratorio De Control Clásico
OBJETIVO
Usar el simulink para crear diferentes funciones de transferencia así como una herramienta capaz de
usarse para la simulación de sistemas.
INTRODUCCIÓN AL SIMULINK
El simulink es un toolbox de matlab que permite simular sistemas de control por medio de diagramas
de bloque.
Para arrancar simulink, entramos a matlab, y ahí se teclea simulink, como se muestra en la siguiente
figura
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
14
Practica 1 Aprendamos MatLab y Simulink
Al entrar al simulink, se nos muestra las bibliotecas que contiene, y que son:
•
•
•
•
•
•
Simulink
Aerospace Blockset
CDMA Reference Blockset
Communications Blockset
Constrol System Toolbox…
Etc.
La presentación de las bibliotecas podría cambiar dependiendo de las que se hayan instalado en cada
computadora. La figura también nos muestra en la parte superior, cuatro iconos: para crear un nuevo
modelo, para abrir un modelo ya existente, para fijar la pantalla de bibliotecas de forma que siempre
permanezca visible y por último, el icono para búsqueda de bibliotecas.
Cada una de las bibliotecas de simulink contiene un cierto número de bloques. Hay dos formas de
accesar los bloques componentes de cada biblioteca, al oprimir sobre el signo + de la biblioteca de
simulink, por ejemplo, se obtiene
Esta misma biblioteca, pero con otra presentación, se obtiene oprimiendo el botón derecho del ratón
sobre la biblioteca de simulink y después oprimiendo el botón izquierdo del ratón
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
15
Laboratorio De Control Clásico
sobre el mensaje desplegado
Cada bloque de la biblioteca contiene un subconjunto de bloques que son usados para formar la
simulación deseada. Al hacer doble clic sobre cualquiera de ellos se nos muestran los componentes del
bloque en cuestión, por ejemplo, al seleccionar el bloque de Continuous, se obtiene
Se observan los siguientes componentes de Continuous: Integrador, derivativo, espacio de estado
función de transferencia, etc.
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
16
Practica 1 Aprendamos MatLab y Simulink
Llevaremos a cabo una simulación simple para efecto de aplicar un poco de lo que se ha visto, para
ello, abrimos el menú File, New y seleccionamos Model, para crear la ventana donde efectuaremos la
simulación mencionada anteriormente
Cierre la ventana de Continuous, y en la biblioteca de simulink haga doble clic sobre Sources para tener
accesibles sus componentes, arrastre con el ratón el componente de Sine Wave (Señal senoidal) a la
ventana del modelo. Puede, si así lo desea, cerrar la ventana correspondiente a componentes de
Sources, y posteriormente abrir la de Sinks, para arrastrar el componente Scope (Osciloscopio) hacia la
ventana del modelo, hasta ahora se tiene lo siguiente
Conecte los dos componentes haciendo clic sobre cualquiera de los puntos de conexión y mantenga
oprimido el botón izquierdo del ratón mientras se mueve hacia el otro punto de conexión del
componente.
Una vez conectados, haga doble clic sobre el osciloscopio para abrir la pantalla que se muestra en la
figura anterior. Al iniciar la simulación, oprimiendo el icono indicado en la figura anterior, en la
pantalla del osciloscopio aparecerá la señal correspondiente; como se muestra en la parte izquierda de
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
17
Laboratorio De Control Clásico
la siguiente figura. La figura de la parte derecha se obtiene al oprimir el icono de autoescala del
osciloscopio, icono en forma de catalejos.
Para cambiar las características de la onda senoidal, haga doble clic sobre el componente de Sine Wave
sobre la ventana del modelo, pueden realizarse cambios en la frecuencia, amplitud, fase etc.
Use y observe los iconos del osciloscopio para aumentar y disminuir el tamaño de la gráfica, cambiar
los ajustes del osciloscopio, imprimir y mantener los ejes.
Realizaremos ahora la simulación de la función de transferencia de un sistema de lazo abierto. Abra la
ventana de un nuevo modelo y arrastre los componentes de las bibliotecas correspondientes, de forma
que se tenga lo siguiente
Haga doble clic sobre el componente función de transferencia y realice los cambios siguientes para
obtener la función de transferencia deseada
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
18
Practica 1 Aprendamos MatLab y Simulink
Al ejecutar la simulación deberá observar la siguiente señal del osciloscopio
Cambiemos ahora los parámetros de la simulación para que la señal se inicie en cero. Haga doble clic
sobre el componente Step y cambie el Initial value a 1, como se muestra en la figura siguiente
Oprima el botón OK y ejecute de nuevo la simulación y observe los cambios en la señal dada por el
osciloscopio, la cual debe ser de la siguiente forma
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
19
Laboratorio De Control Clásico
Salve la simulación del modelo abriendo File – Save del menú de la ventana del modelo y abrase uno
nuevo para crear el siguiente diagrama, arrastrando los componentes apropiados. Utilice otras
bibliotecas y abra los componentes haciendo doble clic sobre ellos para ajustarlos.
Cambie los parámetros de la simulación para ajustar el eje del tiempo de acuerdo a las siguientes
figuras
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
20
Practica 1 Aprendamos MatLab y Simulink
TABLA 1. Ordenes de Matlab y Funciones Matriciales
Órdenes y funciones matriciales
usadas normalmente en la Explicación de lo que hacen las órdenes y de lo que significan las funciones
resolución de problemas de matriciales y las sentencias.
ingeniería de control.
abs
angle
ans
atan
axis
bode
clear
clg
computer
conj
conv
corrcoef
cos
cosh
cov
deconv
det
diag
eig
exit
exp
expm
eye
filter
format long
format long e
format short
format short e
freqs
freqz
grid
hold
i
imag
inf
inv
J
length
linspace
log
loglog
logm
logspace
log10
lqe
lqr
Valor absoluto, magnitud compleja
Ángulo de fase
Respuesta cuando no se asigna expresión
Arco tangente
Escalado manual de ejes
Representación en el Diagrama de Bode
Borra el espacio de trabajo
Borra la pantalla gráfica
Tipo de computador
Complejo conjugado
Convolución, multiplicación
Coeficientes de correlación
coseno
coseno hiperbólico
Covarianza
Deconvolución, divición
Determinante
Matriz diagonal
Valores popios y vectores propios
Finalizar programa
Exponencial base e
Matriz exponencial
Matriz identidad
Implementación de filtro directo
Punto fijo escalado a 15 digitos (Ejemplo: 1.33333333333333)
Punto flotante escalado a 15 digitos (Ejemplo: 1.33333333333333e+000)
Punto fijo escalado a 5 digitos (Ejemplo: 1.3333)
Punto flotante escalado a 5 digitos (Ejemplo: 1.3333e+000)
Respuesta en frecuencia de la Transformada de Laplace
Respuesta en frecuencia de la Transformada-z
Dibujar rejilla o cuadricula
Mantener la gráfica actual en la pantalla
−1
Parte imaginaria
Infinito (∞)
Inversa
−1
Longitud del vector
Vectores espaciados linealmente
Logaritmo natural
Gráfica x-y loglog
Logaritmo matricial
Vectores espaciados logaritmicamente
Logaritmo en base 10
Diseño del estimador lineal cuadrático
Diseño del regulador lineal cuadrático
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
21
Laboratorio De Control Clásico
Max
mean
median
min
NaN
nyquist
Ones
Pi
plot
polar
poly
polyfit
polyval
polyvalm
prod
Quit
Rand
rank
real
rem
residue
rlocus
roots
semilogx
semilogy
sign
sin
sinh
size
sqrt
sqrtm
std
step
sum
Tan
tanh
text
title
trace
Who
Xlabel
Ylabel
Zeros
Valor máximo
Valor medio
Mediana
Valor mínimo
No es un número
Respuesta a la frecuencia en el Diagrama de Nyquist
Constante
Pi ( )
Gráfica x-y lineal
Gráfica polar
Polinomio característico
Ajuste de curva polinomial
Evaluación polinomial
Evaluación polinomial matricial
Producto de elementos
Finalizar el programa
Generación de números aleatorios y matrices
Calcula el rango de una matriz
Parte real
Resto ó módulo
Expansión en fracciones parciales
Diagrama del lugar de las raíces
Raíces de un polinomio
Diagrama semilogarítmico x-y(eje-x logarítmico)
Diagrama semilogarítmico x-y(eje-y logarítmico)
Función signo
Seno
Seno hiperbólico
Dimensión de una matriz
Raíz cuadrada
Raíz cuadrada matricial
Desviación estandar
Respuesta a un escalón unitario
Suma de elementos
Tangente
Tangente hiperbólica
Posicionado arbitrario de texto
Titulo de una gráfica
Traza de una matriz
Lista de todas las variables actualmente en memoria
Etiqueta en el eje x
Etiqueta en el eje y
Cero
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
22
Practica 1 Aprendamos MatLab y Simulink
Conversiones de modelos
Matlab tiene órdenes para las siguientes conversiones de modelos:
• Conversión del espacio de estado a función de transferencia (ss2tf)
• Conversión de función de transferencia a espacio de estado (tf2ss)
• Conversión del espacio de estado a ceros-polos (ss2zp)
• Conversión ceros-polos a espacio de estado (zp2ss)
• Conversión de función de transferencia a ceros-polos (tf2zp)
• Conversión ceros-polos a función de transferencia (zp2tf)
• Conversión de tiempo continuo a tiempo discreto (c2d)
Operadores matriciales
Los siguientes signos se utilizan en las operaciones matriciales:
•
•
•
•
•
+
*
^
‘
Suma
Resta
Multiplicación
Potencia
Transpuesta conjugada
Operadores relacionales y lógicos
Los siguientes operadores relacionales y lógicos se utilizan en Matlab:
• <
Menor que
• <=
Menor que o igual a
• >
Mayor que
• >=
Mayor que o igual a
• ==
Igual
• ~=
No igual
• &
AND
• |
OR
• ~
NOT
Observe que “=” se utiliza en una sentencia de asignación, mientras que “==” se emplea en una
relación.
Caracteres especiales
En Matlab se utilizan los siguientes caracteres especiales:
•
•
•
•
•
•
•
[]
()
,
;
:
!
%
Utilizado para formar matices y vectores
Precedencia de operación aritmética
Separa elementos y argumentos de fucnión
final de filas, suprime la impresión
Generación de vectores
Ejecución de orden del sistema operativo
Comentarios
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
23
Laboratorio De Control Clásico
REPORTE
Como reporte además de lo solicitado en los requerimientos generales:
• Portada
• Objetivo
• Marco Teórico
• Desarrollo
• Resultados
• Conclusiones
Deberán incluirse en donde correspondan aplicaciones a ejemplos de las Ordenes de MATLAB y
Funciones Matriciales siguientes:
• sqrt, log, log10, exp, format long, format long e, format short, format short e (aplicándolas a los
mismos datos)
• abs, conj, imag, real (aplicándolas a los mismos datos)
• det, diag, eye, zeros, ones, prod, size, sum (aplicándolas a los mismos datos)
Es necesario presentar las pantallas en el reporte en Word y dar una explicación de cada orden de
MATLAB y explicar como se realizarían manualmente. En las pantallas deberá aparecer la carga de
datos y como son los mismos para varias ordenes se pueden presentar varias ordenes en la misma
pantalla agregando comentarios.
Realizar sobre las mismas matrices las siguientes operaciones:
• Suma
• Resta
• Multiplicación
• Transpuesta
• Inversa
• Multiplicación de una matriz por su inversa
Es necesario presentar las pantallas en Word y explicar como se realizan manualmente cada una de
estas operaciones matriciales. En una pantalla deberá aparecer la carga de datos y como son los mismos
para todas las operaciones se pueden realizar varias operaciones en la misma pantalla.
Realizar las gráficas de respuesta en el tiempo de sen(t), cos(t), tan(t) para dos ciclos completos. En una
pantalla deberán aparecer los carga de los datos y como son los mismos para las tres gráficas en
pantallas separadas se presentara cada gráfica.
Realizar los siguientes ejemplos de simulaciones:
a) En Lazo Abierto para la Función de Transferencia G1 (s ) =
100
con entrada de un
s 2 + 9s + 100
escalón unitario que inicie en un tiempo de dos segundos.
b) En Lazo Cerrado con Retroalimentación unitaria para la Función de Transferencia
G2 (s ) =
100
con entrada de un escalón de valor 2 que empiece en tiempo cero.
s (s + 9)
Para cada simulación hay que incluir en la impresión las pantallas de donde se cargo la entrada, la
función de transferencia, y el dispositivo de salida aclarando cual se escogió y las pantallas donde se
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
24
Practica 1 Aprendamos MatLab y Simulink
acoplaron los parámetros, así como la gráfica de respuesta en el tiempo del sistema todo acompañado
de una explicación clara de cómo se realizo cada paso.
Como complemento se dará un explicación breve de la diferencia entre Respuesta en el Tiempo y
Simulación y como se logra una y otra en Simulink.
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
25
Laboratorio De Control Clásico
M.C. Manuel Amarante Rodríguez
15 de Julio del 2012
26