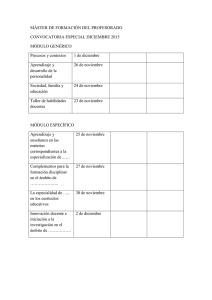
Uso de las inteligencias múltiples en clases de matemáticas
Anuncio

TRABAJO FIN DE ESTUDIOS Título Uso de las inteligencias múltiples en clases de matemáticas Autor/es Álvaro Manuel Martínez Solanas Director/es Roberto Castellanos Fonseca Facultad Facultad de Letras y de la Educación Titulación Máster universitario en Profesorado de ESO, Bachillerato, FP y Enseñanza de Idiomas Matemáticas Departamento Curso Académico 2013/2014 Uso de las inteligencias múltiples en clases de matemáticas, trabajo fin de estudios de Álvaro Manuel Martínez Solanas, dirigido por Roberto Castellanos Fonseca (publicado por la Universidad de La Rioja), se difunde bajo una Licencia Creative Commons Reconocimiento-NoComercial-SinObraDerivada 3.0 Unported. Permisos que vayan más allá de lo cubierto por esta licencia pueden solicitarse a los titulares del copyright. © © El autor Universidad de La Rioja, Servicio de Publicaciones, 2014 publicaciones.unirioja.es E-mail: [email protected] MÁSTER EN PROFESORADO DE ESO, BACHILLERATO, FP Y ENSEÑANZA DE IDIOMAS ESPECIALIDAD: MATEMÁTICAS CURSO 2013-14 USO DE LAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS ÁLVARO MANUEL MARTÍNEZ SOLANAS TUTOR: ROBERTO CASTELLANOS FONSECA TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS ÍNDICE 1. INTRODUCCIÓN ___________________________________________________ 4 2. MARCO TEÓRICO SOBRE LOS PROCESOS DE ENSEÑANZA-APRENDIZAJE ______ 6 3. 2.1 TEORÍAS DEL APRENDIZAJE ____________________________________________ 8 2.2 TEORÍAS DE APRENDIZAJE DE LAS MATEMÁTICAS _________________________ 13 2.3 LA ADOLESCENCIA __________________________________________________ 19 ELEMENTOS FUNDAMENTALES DE LA MEMORIA DE PRÁCTICAS ___________ 21 3.1 ANÁLISIS DEL CENTRO EDUCATIVO _____________________________________ 21 3.2 ORGANIZACIÓN DE LAS PRÁCTICAS ____________________________________ 22 3.3 DESCRIPCIÓN DEL GRUPO-CLASE_______________________________________ 24 3.4 PROCESOS DE ENSEÑANZA-APRENDIZAJE EN LA INTERVENCIÓN EN EL AULA ___ 30 3.5 UNIDAD DIDÁCTICA DE INTRODUCCIÓN A LAS DERIVADAS Y SUS APLICACIONES. 1º BACHILLERATO CIENCIAS SOCIALES _________________________________________ 31 4. 3.6 OTRAS ACTIVIDADES REALIZADAS______________________________________ 49 3.7 REFLEXIONES SOBRE LAS PRÁCTICAS ___________________________________ 50 PROYECTO DE INNOVACIÓN E INVESTIGACIÓN EDUCATIVA _______________ 55 4.1. INTRODUCCIÓN Y CONTEXTUALIZACIÓN ________________________________ 55 4.2. JUSTIFICACIÓN-MOTIVACIÓN DEL PROYECTO Y OBJETIVO __________________ 58 4.3. MARCO TEÓRICO VS FUNDAMENTACIÓN ________________________________ 62 4.4. DESCRIPCIÓN DEL PROYECTO VS INNOVACIÓN ___________________________ 79 4.5. METODOLOGÍA_____________________________________________________ 86 Página 2 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.6. EVALUACIÓN ______________________________________________________ 92 4.7. REFLEXIONES FINALES Y CONCLUSIONES _______________________________ 106 5. REFERENCIAS Y BIBLIOGRAFÍA _____________________________________ 109 6. APÉNDICES _____________________________________________________ 113 7. ANEXOS _______________________________________________________ 114 7.1 ANEXO 1: ACTIVIDADES DE LA UNIDAD DIDÁCTICA DE DERIVADAS DE 1º BACHILLERATO DE CIENCIAS SOCIALES. _______________________________________ 114 7.2 ANEXO 2: RECURSOS UTILIZADOS _____________________________________ 121 7.3 ANEXO 3: RECURSOS Y MATERIALES DE APOYO A LA DOCENCIA ____________ 124 7.4 ANEXO 4: TEMPORALIZACIÓN DE SESIONES UNIDAD DIDÁCTICA DE 1º BACH __ 126 7.5 ANEXO 5: ACTIVIDADES DE TIPO JUEGOS _______________________________ 128 7.6 ANEXO 6: ACTIVIDADES TIPO LABORATORIO VIRTUAL O PRESENCIAL ________ 138 7.7 ANEXO 7: ACTIVIDADES DE FOMENTO DE LA CREATIVIDAD MATEMÁTICA ____ 145 7.8 ANEXO 8: ESCALAS DE EVALUACIÓN DE INTELIGENCIAS MÚLTIPLES _________ 149 Página 3 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 1. INTRODUCCIÓN El presente Trabajo Fin de Master (TFM), consiste en el compendio de todos los saberes y habilidades adquiridos durante el transcurso de 1 año en el que se ha recibido formación del Master de Profesorado de Educación Secundaria, Bachillerato, Formación Profesional y Enseñanzas de Idiomas a través de las diferentes asignaturas, así como, de los elementos más destacados de la experiencia como docente en prácticas en un centro de educación secundaria obligatoria (ESO). Además de incluir un proyecto de innovación e investigación docente de la especialidad que se ha cursado del máster (matemáticas). Tal y como recoge la guía del Máster (1) los objetivos fundamentales son: 1. Capacitar a los futuros docentes para enseñar de manera adecuada al nivel y a la formación previa de los estudiantes, las materias correspondientes a cada especialidad. 2. Formar a los docentes en habilidades que les permitan actuar profesionalmente como miembros de un equipo docente. 3. Incorporar en su formación aquellos saberes académicos y profesionales que les permitan desarrollar de forma adecuada su labor y les faciliten conseguir una formación integral en sus estudiantes. Estos objetivos son conseguidos a través de las diferentes asignaturas presentes en el plan de estudios de máster de la Universidad de La Rioja, que se dividen en dos partes bien diferenciadas: las clases teóricas impartidas a lo largo de todo el curso (47 ECTS) y el periodo de prácticas curriculares de dos meses de duración en un centro de educación secundaria (13 ECTS). Así mismo, el contenido teórico está separado en Página 4 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS asignaturas de habilidades comunes y asignaturas propias de la especialidad elegida, en este caso matemáticas, las cuales son: Asignaturas del bloque común (impartidas a lo largo del primer cuatrimestre, con la misma carga de créditos ECTS, 4,5): Aprendizaje y desarrollo de la personalidad (Psicología). Sociedad, familia y educación (Sociología). Procesos y contextos educativos (Pedagogía). Asignaturas específicas de la especialidad: Aprendizaje y enseñanza de las matemáticas. Impartida a lo largo de los dos cuatrimestres, con una carga de 15 ECTS. Complementos para la formación disciplinar. Impartida a lo largo de los dos cuatrimestres, con una carga de 6 ECTS (formación complementaria e histórica sobre matemáticas). Innovación docente e iniciación a la investigación educativa. Impartida a lo largo del segundo cuatrimestre, con una carga de 6 ECTS. En la primera parte de este TFM, se realiza un breve resumen del marco teórico sobre el que versa la formación de este Máster y sobre las distintas teorías de aprendizaje existentes, además de realizar un breve estudio sobre las principales características pedagógicas, psicológicas y sociales de los adolescentes. En segundo término, se presentan los elementos fundamentales de la Memoria de Prácticas, contemplando las actividades realizadas y una reflexión sobre las mismas. Y por último, se acomete un proyecto de innovación educativo que trata sobre la aplicación de la teoría de las inteligencias múltiples en las clases de matemáticas. Página 5 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2. MARCO TEÓRICO SOBRE LOS PROCESOS DE ENSEÑANZA-APRENDIZAJE Son muchas las habilidades y características que se deben dar en una persona que esté motivada por ofrecer conocimientos a los demás. Después de haber cursado este máster, los aspectos más importantes para mi futuro profesional, son los siguientes: El profesor es la guía que ayuda al alumno avanzar en sus conocimientos. El profesor dispone de un gran bagaje cultural para enriquecer la docencia en la medida de las necesidades de cada momento. El profesor motiva y orienta a los alumnos en función de sus inquietudes. El profesor dispone de una gran estabilidad emocional. El profesor es el nexo de unión entre muchos contextos de la sociedad. Seguro que hay otros muchos aspectos igual de importantes que los que cito, ya que la labor de un profesor abarca un gran espectro de posibilidades. Como se puede ver, cada una de las citas, está en cierta manera enmarcada en cada asignatura del máster. En primera lugar, es fundamental comprender que para el desarrollo de la enseñanza y el aprendizaje, no existen recetas universales y que cada persona es diferente de las demás con sus peculiaridades, por ello todos esos saberes de los que dispone el profesor deben ser puestos en práctica de la forma más adecuada para conseguir el mejor desarrollo cognitivo, educativo, emocional… del alumno. Aspectos, estos, incluidos en el programa de la asignatura de Psicología y en la de Enseñanza. Otro de los aspectos más importantes a mi modo de ver, es que si bien el profesor no debe saber todo de todo, debe disponer de un gran baúl de conocimientos y Página 6 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS saberes que le permitan ofrecer un gran abanico de posibilidades y enseñanzas, adecuadas a cada grupo de alumnos y a cada momento de la sociedad. Aspectos referidos en los programas de las asignaturas Complementos e Innovación (Historia). Por otro lado, desde los conocimientos adquiridos en la asignatura de Pedagogía, uno de los puntos a tener en cuenta en la sociedad del futuro, es la motivación. Tanto estudios psicológicos, como pedagógicos muestran que la verdadera semilla de todo aprendizaje reside en la motivación y el interés y que en la sociedad del conocimiento y de la tecnología en la que nos encontramos, el profesor debe conocer las inquietudes de sus alumnos para poder adaptar mejor los contenidos curriculares a la enseñanza de la materia en cuestión. Debido a toda la carga emocional que supone la tarea del docente y la cantidad de sentimientos, problemáticas, situaciones e inquietudes que el profesor debe canalizar, poniéndolas en sincronía con su situación personal, una de las principales características que a mi modo de ver debe tener un profesor, es la gran estabilidad emocional, para producir unos ambientes de aprendizaje adecuados en cada momento y transmitir a su entorno un ejemplo de actitud. Aspectos, estos, incluidos en el programa de la asignatura de Psicología. Todos los aspectos anteriores son debidos a que vivimos como seres sociales que vivimos y nos relacionamos en sociedad (ya sea real o virtual). En muchas ocasiones se produce un desarrollo de roles sociales y entornos naturales sin ningún patrón de ejemplo, pero siempre es necesario la labor de los profesores para posibilitar la mayor interconexión de agentes sociales en la formación de las personas, para que estas tengan un desarrollo integral y completo para su futura coexistencia en sociedad. Aspectos referidos en el programa de la asignatura de Sociología. Página 7 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2.1 TEORÍAS DEL APRENDIZAJE El aprendizaje es el proceso a través del cual se adquieren o modifican habilidades, destrezas, conocimientos, conductas o valores como resultado del estudio, la experiencia, la instrucción, el razonamiento y la observación. Este proceso puede ser analizado desde distintas perspectivas, por lo que existen distintas teorías del aprendizaje. El aprendizaje es una de las funciones mentales más importantes en humanos, animales y sistemas artificiales. (2). Por otro lado, cabe destacar el punto de inflexión que el Doctor en Educación por la Universidad de Londres, Sir Ken Robinson, propone en sus teorías sobre la creatividad de los niños, supone un cambio de paradigma, muchas veces poco evidente. Su planteamiento radica en dejar desarrollar la creatividad de los niños más allá de facilitársela o adecuar el entorno a ellos como dice el constructivismo, para dejar nacer una nueva sociedad sin las ataduras del pasado, cuyas teorías en parte están condicionadas por la grave situación de crisis moral, política, sistémica y vital en la que se encuentra la sociedad de principios de siglo XXI. (3). Existen diversas teorías del aprendizaje, mediante las cuales los seres humanos transmiten y aprenden conocimientos, algunas de las cuales se tratan a continuación. 2.1.1. Conductivismo (Modelo conductista) El conductismo (4), según su fundador John Broadus Watson (5), es una escuela natural que se atribuye todo el campo de las adaptaciones humanas, es decir, que el desarrollo del ser humano está marcado por su aprendizaje y que ese aprendizaje va en función de las influencias ambientales. Para Iván Pavlov (6), el ser humano aprende por detección de regularidades o relaciones entre estímulos (condicionamiento clásico). Por Página 8 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS otro lado, para Burrhus Frederic Skinner (7) se trata de una filosofía de la ciencia de la conducta (condicionamiento operante), que define varios aspectos esenciales de su objeto de estudio. En todos estos autores, el ser (en este caso el alumno), es un agente pasivo en el proceso de aprendizaje, en el que se da un proceso de almacenamiento y no de reflexión. Además para ellos los cambios biológicos no anteceden a las conductas (diferenciándose de las teorías innatistas, genetistas y etológicas del desarrollo del ser humano (8)(9)(10)), dejando de un lado los posibles talentos, inclinaciones, tendencias, aptitudes o vocaciones que puedan tener. Es un modelo de aprendizaje que trata de obtener respuestas correctas, despreocupándose de cómo se llegan hasta ellas. Criticas al modelo conductista La principal crítica al modelo conductista es que trata al ser humano de una manera muy simplista como una máquina vacía que recibe información y que produce unos resultados en base al modelo que ha aprendido. Supone una parada en la evolución del intelecto humano, ya que no reflexiona sobre lo aprendido. Otra de las críticas a este modelo es que asume que todos los seres humanos son iguales, sin diferencias biológicas, aptitudinales, vocacionales o intelectuales, ofreciendo una formación no individualizada. Este modelo parte de la revolución industrial por ello, en su época en cierta manera tenía sentido enseñar mecanismos de pensamiento y desarrollo propios de una máquina, de modo que la sociedad permaneciera en un continuo proceso de producción infinito. Página 9 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2.1.2. Cognitivismo (Modelo constructivista) La psicología cognitiva es la psicología que se encarga del estudio de la cognición; es decir, de los procesos mentales implicados en el conocimiento. Tiene como objeto de estudio los mecanismos básicos y profundos por los que se elabora el conocimiento, desde la percepción, la memoria y el aprendizaje, hasta la formación de conceptos y razonamiento lógico. Por cognitivo entendemos el acto de conocimiento, en sus acciones de almacenar, recuperar, reconocer, comprender, organizar y usar la información recibida a través de los sentidos. (11). Así mismo, el modelo constructivista, postula la necesidad de entregar al alumno herramientas (generar andamiajes) que le permitan crear sus propios procedimientos para resolver una situación problemática, lo cual implica que sus ideas se modifiquen y siga aprendiendo. El constructivismo educativo propone un paradigma en donde el proceso de enseñanza se percibe y se lleva a cabo como un proceso dinámico, participativo e interactivo del sujeto, donde el alumno es un agente activo, de modo que el conocimiento sea una auténtica construcción operada por la persona que aprende (por el "sujeto cognoscente"). El constructivismo en pedagogía se aplica como concepto didáctico en la enseñanza orientada a la acción. (12). Algunas de las figuras clave de este modelo son Jean Piaget (se centra en las formas más sencillas de inteligencia para explicar los modos de inteligencia más complejos, es decir, la construcción del conocimiento partiendo de la interacción con el medio). Este autor supone ya un gran salto respecto al conductismo, ya que para Piaget, un niño inteligente es aquel que es capaz de explicar cómo ha llegado a la adquisición de un conocimiento y además sabe adaptarse al medio lo mejor posible. Otro de los autores más destacados de este modelo es Lev Vigotsky, cuyo planteamiento todavía va Página 10 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS más allá, y es que en este autor la construcción del conocimiento es un producto de la interacción social. Cabe destacar también, autores como Albert Bandura y Bruner, que defienden un planteamiento en el que la educación es la mediadora ente el individuo y el medio histórico-cultural en el que se desarrolla, asumiendo que la educación debe adaptarse al entorno sociocultural para enseñar a vivir en sociedad. Criticas al modelo cognitivista Este modelo asume una gran influencia del entorno sin dejar de lado las características del individuo, por ello se puede caer en la excesiva atención del alumno que le lleve a asumir que es el centro de todo tanto para sus padres como para los profesores y de esta manera adecuar el proceso a sus exigencias, minimizando el contenido mínimo que se pudiera exigir para un desarrollo correcto y eliminando la capacidad de esfuerzo por mera antipatía. Este es un modelo que actualmente tiene gran acepción en los centros, pero que raramente se lleva a cabo en su totalidad por la gran cantidad de recursos y de esfuerzos que conlleva, además de que en muchas ocasiones se queda en meras palabras y que no todos los docentes actuales están capacitados para asumir este reto. 2.1.3. Neuropsicología Los avances científicos de estos últimos años han posibilitado dar nuevos enfoques a la psicología del aprendizaje, como es la neuropsicología. (13). Esta ciencia trata sobre el estudio de las estructuras cerebrales y de las funciones de dichas estructuras. Es el marco de referencia para el estudio y la explicación del funcionamiento y la naturaleza de los diferentes patrones de desarrollo. La Página 11 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS neuropsicología concibe la inteligencia como un constructo que abarca las interrelaciones existentes entre la personalidad, las estrategias de afrontamiento, los procesos motivacionales, el esfuerzo y que es dinámico y no estable a lo largo del tiempo (Inteligencias múltiples de Howard Gardner. (14)). Y por último, concluye que las relaciones entre las bases neuronales y las experiencias producen representaciones mentales dinámicas en base a múltiples factores, que definen nuestros patrones de comportamiento en cada momento. Algunos de los defensores de estas teorías de aprendizaje es Lui H. Colon (16), que defiende que el cerebro es el único órgano en el universo que conocemos, que puede observarse, analizarse y modificarse a sí mismo. “No importa la edad que tengamos, mientras sigamos utilizando nuestro cerebro, éste nos seguirá respondiendo”. Y es que nunca sabremos cuánta capacidad de almacenaje y creación tiene, ya que, mientras más se educa al cerebro, más y más puede aprender. Otros como, el doctor en ciencias de la educación Ken Robinson (3), defienden que el aprender a ser creativo es la base para activar todas las potencialidades de nuestro cerebro, por lo que defiende la incorporación de las clases de arte en el currículo escolar. Los modelos de aprendizaje que se pueden asimilar más fácilmente desde estas teorías, son los modelos de las inteligencias múltiples. Crítica a las teorías de la neuro-psicología Desde estas teorías se puede llegar a pensar que solo el entorno puede llegar a cambiar nuestro cerebro, pero también tienen en cuenta la predisposición genética del mismo (GENÉTICA + AMBIENTE), por ello las teorías de aprendizaje desarrolladas en base a la neuropsicología todavía son muy incipientes y nada congruentes y de Página 12 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS momento nos tenemos que conformar con las teorías cognitivistas, en las que se tiene en cuenta tanto el ambiente como la genética, aunque los resultados no sean los mejores. Deja un amplio espacio vacío en el que desarrollar modelos de aprendizaje, pero presenta desde mi punto de vista un riesgo y es que para conseguir conocer esos modelos, en base a estas teorías, de momento las técnicas como el TAC y el PET, no están orientadas al aprendizaje sino al diagnóstico de cerebros enfermos y a experimentaciones en cada caso. Las experiencias de utilización de modelos basados en la teoría de las inteligencias múltiples están todavía en fase de experimentación y en los próximos años podremos saber más sobre los mismos. (15). 2.2 TEORÍAS DE APRENDIZAJE DE LAS MATEMÁTICAS A lo largo de la historia de las matemáticas, ésta disciplina ha formado parte del sistema de educación de civilizaciones antiguas. En la mayoría de los casos la educación formal estaba destinada a las personas más privilegiadas de la sociedad, cuyos avances fueron de gran utilidad para las épocas posteriores, pero cuyos esfuerzos en investigación y aprendizaje, eran totalmente distintos a lo que hoy conocemos. No se planteaban si la educación y la transmisión de saberes debía de ser de otra forma (conductismo, cognitivismo…), directamente los más sabios de la sociedad se reunían para intentar desarrollar nuevas teorías, eso sí compartiendo, poniendo en común, trabajando y con una gran capacidad de esfuerzo. En la época de la revolución industrial, se entendía que se debía enseñar las matemáticas esenciales para desenvolverse en el nuevo estilo de vida urbano. Página 13 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Hoy en día, en la mayor parte de países civilizados la educación matemática se contempla en la educación básica a través de los currículos de la administración educativa correspondiente, (cada país con sus peculiaridades), estableciendo los mínimos educativos a los que cualquier adolescente debe llegar, desglosándolos en competencias, a las que no en todas las ocasiones se llega de la misma manera y que no en todos los países son iguales (por ejemplo en países como Cuba, Rusia o China una de las asignaturas incluidas en los currículos es el ajedrez y las matemáticas abstractas, cosa que en el mundo occidental no es así). No dan tanta importancia a la forma en que impartir la docencia, aunque mediante las competencias o habilidades mínimas y el tiempo en que hay que alcanzarlas en cierta manera enmarcan o limitan estas formas. Vivimos unos tiempos en los que la mayor parte de la población está alfabetizada o al menos eso debería ser. Además los progresos y avances científicotecnológicos nos obligan a ello. Por lo tanto, es de gran necesidad poder atender las necesidades de toda la población, cosa que antes ni se planteaba. Desde este planteamiento inicial, lo primero que hay que pensar es que los niños y los adolescentes no se deben conformar con aprender de memoria los aspectos superficiales y conceptos tradicionales de las matemáticas, sino que deben ser capaces de resolver por sí mismos cualquier problema que se les pueda plantear, sea de la índole que sea, en base a unas pautas y conocimientos adquiridos que les permitan tener herramientas mentales y actitudinales para ello, debido al mundo tan cambiante en el que vivimos. No por ello, debemos dejar atrás las matemáticas que se alejen de la realidad, por el mero hecho de no tener utilidad real, ya que en muchas ocasiones el avance matemático puede descubrir cosas por sí solo, sin necesidad de estar ligado a la realidad de su tiempo y por ello también hay que saber transmitirlo. Página 14 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS En la actualidad, según los informes del PISA dentro de la OCDE de 2014 los resultados en matemáticas en España han bajado, pero cabe pensar si estas pruebas representan correctamente los conocimientos que los adolescentes tienen en relación a las matemáticas. Es cierto que en la sociedad existe una cierta aversión a los contenidos matemáticos que muchas veces provoca estos malos resultados (solo con la motivación se podría aprender cualquier cosa), pero no por ello los conocimientos matemáticos de la sociedad son insuficientes. Los alumnos tienden a sentir respeto por la asignatura debido a los cliches sociales que se crean entorno a la misma, pero debemos hacer un esfuerzo conjunto para superarlos y encontrar la forma óptima de enseñar las matemáticas y los procesos cognitivos que subyacen en la ejecución matemática de nuestro tiempo. 2.2.1. Desarrollo del pensamiento matemático A lo largo de la historia de la psico-pedagogía, el estudio y aprendizaje de las matemáticas se ha realizado desde perspectivas muy distintas. Desde hace tiempo han coexistido dos formas bien diferenciadas, la del aprendizaje de habilidades matemáticas elementales basado en la práctica por un lado, y por otro, el aprendizaje de los métodos de razonamiento matemático que centraba su enseñanza en los conceptos. Entre los autores más destacados, podemos destacar a Edward Thorndike (modelo de asociacionismo (17)), William Brownell (modelo de comprensión y reflexión (18)) también defendido por Piaget o los modelos de integración de habilidades defendidos por David Ausubel, Jerome Bruner, Robert M.Gagné o Lev Vigotsky, más relacionados con la teoría de las inteligencias múltiples de Howard Gardner que deja un amplio campo todavía por desgranar. Página 15 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Los diferentes conocimientos matemáticos en casi todos los países civilizados se enseñan en función de la edad del alumno, en secuencias diferentes según el país y el modelo educativo. Primero se ofrecen los conocimientos de las matemáticas básicas en casi todos los países de manera similar y después se empieza por el conocimiento de los números y la aritmética, continuando por el álgebra y la geometría y finalizando con el análisis y la estadística (probabilidad), donde ya hay más divergencias entre países. Para saber cómo debe ser el aprendizaje de las matemáticas en los niños, es necesario conocer los tipos de pensamiento y conocimiento matemático que poseen, entre los que podemos distinguir los siguientes: Conocimiento intuitivo: Se entiende como conocimiento intuitivo, el sentido natural del número que tiene un niño (suele ser de manera imprecisa y muy limitada, aunque si son sensibles al cambio de cantidades de objetos), las nociones de magnitud y equivalencia o las nociones de adición y sustracción. Conocimiento informal: El niño a medida que va creciendo se va dando cuenta que no basta con esos conocimientos intuitivos y que necesita contar y numerar (normalmente suele darse después de empezar a hablar). De esta forma se dan cuenta de que las etiquetas numéricas no están ligadas a los objetos y que sirven para especificar conjuntos equivalentes. Es decir, el nivel de abstracción en el niño aumenta y por ello son cada vez más propensos al error. Conocimiento formal: Debido a la corrección y a no querer cometer errores el niño cuando empieza a alcanzar la etapa de adolescente necesita adquirir un mayor grado de formalismo a la vez que de abstracción, para poder asimilar mejor la realidad que le rodea. Página 16 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS En la adolescencia, el alumno es capaz de ver la necesidad y la utilidad de adquirir rigor matemático, visualizar figuras, analizarlas, hacer estudios estadísticos con mayor precisión, manejarse con el lenguaje matemático para su vida diaria, es decir, las habilidades o como se llama ahora competencias que marcan los currículos en matemáticas y que a medida que el adolescente va subiendo de “peldaño” va siendo capaz de alcanzar mayor conocimiento matemático. En la adolescencia se ofrecen todas las destrezas matemáticas en todos los niveles, pero cada uno con una dificultad diferentes y que requiere del anterior para poder avanzar. 2.2.2. Tipos de competencia matemática La competencia matemática según el informe PISA, es la capacidad de un individuo para identificar y entender la función que desempeñan las matemáticas en el mundo, emitir, juicios fundados y utilizar y relacionarse con las matemáticas de forma que se puedan satisfacer las necesidades de la vida de los individuos como ciudadanos constructivos, comprometidos y reflexivos. Dentro de esta competencia, se evalúan la capacidad para plantear, formular e interpretar problemas de diferentes contextos, así como la capacidad de analizar, razonar y comunicar ideas matemáticas de forma efectiva. Estas capacidades que PISA propone para evaluar se pueden resumir en 3, reproducción, conexiones y reflexión. La mayor parte de las teorías psicológicas comparten el objetivo de comprender el comportamiento del alumno a la hora de enfrentarse a las matemáticas, pero difieren en los análisis que adoptan (conductual, fisiológico o cognitivo), en las áreas de conducta (social, emocional e intelectual) y en las situaciones hacia el alumno (personal, educacional, pública o científica), por lo tanto todavía no somos capaces de interpretar y evaluar correctamente el aprendizaje de nuestros alumnos en matemáticas. Página 17 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Por ello para comprender los tipos de aprendizaje de los alumnos se debe saber cómo se han producido en cada una de estas áreas y así poder confeccionar un árbol con las diferentes trayectorias de aprendizaje de matemáticas vividas. (19). Para ello suele ser muy útil el proceso de matematización de problemas propuesto por el informe PISA que consiste en los siguientes pasos. Figura 1: Proceso de Matematización PISA 1 Así como otras técnicas como es, la diferenciación de contenidos en la ejecución de problemas (resolver el mismo problema para diferentes niveles de dificultad). 2.2.3. Dificultades en el aprendizaje de las matemáticas Existen una serie de factores de riesgo que es necesario tener en cuenta con los alumnos, a la hora de realizar la enseñanza de las matemáticas. La vulnerabilidad y el grado de resistencia a agentes adversos varían de unos alumnos a otros. La siguiente lista muestra algunos de los factores principalmente influyentes: - Constitucionales: Influencias hereditarias y anomalías genéticas, complicaciones prenatales y durante el nacimiento, enfermedades y daños sufridos después del nacimiento, alimentación y cuidados médicos inadecuados. Página 18 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS - Familiares: Pobreza, malos tratos, indiferencia, conflictos, desorganización, psicopatología, estrés, familia numerosa. - Emocionales e interpersonales: Patrones psicológicos tales como baja autoestima, inmadurez emocional, temperamento difícil, incompetencia social, rechazo por parte de iguales. - Intelectuales y académicos: Trastornos del aprendizaje. Fracaso escolar. - Acontecimientos de la vida no normativos que generan estrés: Muerte prematura de los progenitores. Estallido de una guerra en el entorno inmediato. - Ecológicos: Vecindario desorganizado, ruidoso y con delincuencia. Injusticias raciales, étnicas y de género. 2.3 LA ADOLESCENCIA El Master de Profesorado está orientado a la formación de docentes de Educación Secundaria, Bachillerato, Formación Profesional y Escuelas de Idiomas. Por tanto, las clases en las que hay que impartir docencia en su mayoría estarán formadas por adolescentes. Un objetivo fundamental, por tanto, es conocer qué inquietudes tienen y qué cambios les suceden a los alumnos en esta etapa, para que podamos comprender mejor la realidad del aula. La adolescencia es un periodo en el desarrollo biológico, psicológico, sexual y social inmediatamente posterior a la niñez y que comienza con la pubertad. Tiene una duración variable en cada persona, pero se considera que esta etapa empieza alrededor de los 10 años y dura hasta los 19 (según la OMS). Es esencialmente una época de Página 19 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS cambios, es la etapa que marca el proceso de transformación del niño en adulto, es un periodo de transición que tiene características peculiares. Es una etapa de descubrimiento de la propia identidad, así como de la de autonomía personal. A pesar de que esta etapa se puede dividir en distintas fases y que el ritmo de desarrollo es distinto en chicas y en chicos, en ambos sexos existen características comunes que debemos conocer. Los rasgos cognitivos más característicos son: - Idealismo. - Tendencia a la indecisión y a discutir con el objetivo de poner a prueba sus capacidades de razonamiento. - Egocentrismo. Audiencia pública imaginaria. El adolescente se siente el centro de atención y está muy preocupado por lo que los demás piensan de él. - Invencibilidad. El adolescente piensa que él no puede ser víctima de conductas peligrosas. Por eso asume todo tipo de riesgos y no toma las precauciones necesarias. Comprender estas características nos resultará muy útil para saber cómo son nuestros alumnos, que como ya hemos dicho en la introducción, es algo fundamental para un docente. El hecho de que las chicas se desarrollen antes que los chicos, provoca que en una clase haya diferencias de madurez entre alumnos, y por tanto, debemos tenerlo en cuenta en nuestro método docente. El objetivo final es conocer a las personas a las que se va a impartir clase para intentar conseguir el método de enseñanza más adecuado para ellos. Página 20 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3. ELEMENTOS FUNDAMENTALES DE LA MEMORIA DE PRÁCTICAS 3.1 ANÁLISIS DEL CENTRO EDUCATIVO Las prácticas del Máster de Profesorado de Educación Secundaria, Bachillerato, Formación Profesional y Escuelas de Idiomas, se han realizado en el centro IES Batalla de Clavijo, de Logroño (La Rioja), situado en la calle General Urrutia Nº34, en la zona urbana céntrica de la ciudad al lado de un parque municipal y el rio Ebro. La mayor parte del alumnado de secundaria que acude al centro proviene del barrio en el que se encuentra situado el centro, concretamente del C.P. Navarrete El Mudo, caracterizado por alumnos con necesidades especiales por proceder de minorías étnicas, desestructuración familiar y alto absentismo escolar con un gran porcentaje de población inmigrante de diferentes origines y culturas, además de una tasa elevada de paro, así como alumnado autóctono propio de la comunidad con las capacidades adecuadas al nivel de ESO exigible. El alumnado de bachillerato y formación profesional (los más numerosos en este centro) provienen de las diferentes zonas urbanas y rurales de la Comunidad Autónoma de La Rioja, motivados tanto por el interés en el bachillerato de artes (único centro en La Rioja que ofrece esta formación, de ahí el elevado número de alumnado), como por formaciones más técnicas por su bachillerato de ciencias sociales y sus grados superiores de Construcción, Educación Infantil, Animación Sociocultural e Integración Social. Debido tanto al desarrollo educativo del centro como a la progresión en el tipo de alumnado residente en el mismo, una de las características fundamentales del Página 21 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS profesorado del mismo es la de ofrecer una enseñanza de calidad a todos los alumnos, respetando la pluralidad de los mismos, persiguiendo formar personas críticas y comprometidas, capaces de intervenir de manera solidaria y constructiva en la sociedad del momento y en el medio ambiente. La metodología de enseñanza utilizada en el centro es muy dinámica incluyendo medidas curriculares y organizativas para hacer posible alcanzar las metas definidas en su programación. 3.1.1. Equipamiento del centro El equipamiento y los recursos con los que cuenta el Instituto de Educación Secundaria Batalla de Clavijo, son acordes a la oferta formativa tanto en Educación Secundaria, Bachillerato y Ciclos Formativos que el centro ofrece. 3.2 ORGANIZACIÓN DE LAS PRÁCTICAS Mi periodo de prácticas tuvo lugar entre el 28 de Febrero y el 26 de Abril de 2014, e incluyeron las asignaturas impartidas por mi tutor (Matemáticas de 2ºESO A y B, 1º Bachillerato Ciencias Sociales, 1º ESO Adaptación Curricular), aunque con permiso del centro y de otros profesores de otras materias, también pude completar mi horario semanal con la asistencia como oyente a otros grupos de clase como fue Técnicas de Arquitectura del Bachillerato Artístico. Mi horario de asistencia al centro era de 8:00 a 14:00. Durante las semanas de prácticas se pueden distinguir tres periodos diferenciados: Página 22 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.2.1. Primer periodo (de observación) Este periodo duró aproximadamente 2 semanas, según el grupo, durante las cuales fui familiarizándome con las clases. Durante este tiempo asistí a las diferentes asignaturas y pude comprobar la labor de mi profesor tutor. Aproveché estas semanas para evaluar el ritmo de aprendizaje de los alumnos, sus reacciones, la forma en la que se comportan y las dificultades que aparecen. También me sirvió para aprender el nombre de los alumnos y ver cuáles eran sus inquietudes, además de aprovechar para familiarizarme con el centro y con su PEC. 3.2.2. Segundo periodo (de docencia) Este periodo duró aproximadamente 5 semanas, durante las cuales fui adoptando paulatinamente mayores cotas de participación en el aula, con el acompañamiento de mi tutor. Fue de gran interés para mi formación ya que pude comprobar todas mis habilidades y otras nuevas que no conocía con los alumnos, además de aprender a chequear cuales son las necesidades de conocimientos de mis alumnos para poder adaptar las clases día a día. 3.2.3. Tercer periodo (de reflexión y redacción de la memoria) Este periodo duró aproximadamente 2 semanas, durante el cual pude redactar en colaboración con los profesores del departamento, mi tutor, el coordinador y otros agentes del centro, mi memoria de prácticas. Durante este tiempo pude compartir opiniones con otros docentes de otras materias y puntos de vista sobre la educación. Página 23 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.3 DESCRIPCIÓN DEL GRUPO-CLASE 3.3.1. Características psicopedagógicas de los alumnos Las principales características psicopedagógicas de los alumnos que se ha atendido durante la duración de las prácticas de este Master, son las siguientes: 1º ESO (Compensatoria): Algunos de los alumnos de esta clase presentan problemas de comportamiento muy graves que pueden impedir el desarrollo normal del curso y por lo tanto de sus compañeros. Dos de los cuales tienen su origen en el riesgo que supone el cambio de primaria a secundaria durante la adolescencia, ambos todavía son psicológicamente niños de primaria pero en cuerpos de adolescentes, que todavía no se ubican en qué etapa se encuentran, además presentan un trastorno disocial, debido a la desestructuración de sus familias, en ambos desafiante aunque no de manera continua. En el caso de los alumnos procedentes de etnia gitana, se encuentran en un momento en el que su cerebro está intentando dirimir entre qué modelo de persona va a ser, eliminando las conexiones cerebrales y ejemplos vividos durante su anterior etapa para quedarse con lo que realmente le sea útil, por ello es muy necesario hacer gran hincapié en este alumno para que su desarrollo futuro sea el correcto y no el fácil y rápido derivado de su etnia gitana. En el caso de otro de los alumnos, también presenta en algunos casos un trastorno disocial desafiante debido a la situación familiar en la que se encuentra. Por otro lado, una de las alumnas presenta un gran absentismo escolar además de una enfermedad que no le permite asistir a las clases con continuidad. Por ultimo cabe destacar la capacidad de imaginación de dos del resto de alumnos de la clase, presente en cualquier momento de las clases. Todos estos aspectos se están Página 24 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS tratando con los servicios sociales pero no en todos los casos se consiguen los resultados esperados. 2º ESO (A): Existen alumnos con graves problemas de comportamiento que pueden impedir el desarrollo normal de las clases y por lo tanto influir en el progreso académico de sus compañeros negativamente. En algunos casos, estos problemas tienen su origen en la desestructuración familiar presente en sus casas, lo cual requiere una atención personalidad y diaria. En otro de los casos, simplemente es la inmadurez típica de los adolescentes de su edad y una posible inestabilidad familiar. Dos de los alumnos requieren una adaptación de conocimientos debido a sus altas capacidades aun sin diagnósticar. 2º ESO (B): Existen algunos alumnos con conducta disocial, completamente aversiva al estudio y de carácter desafiante hacia el profesorado. Otros presentan graves problemas de comportamiento que impiden el desarrollo normal de la asignatura y con ello impiden el progreso académico de sus compañeros. Existen alumnos (ACNE) con un grupo de apoyo correspondiente por sus deficiencias cognitivas idiomáticas y conceptuales. 1º Bachillerato Ciencias Sociales: Algunos de los alumnos presentan dificultades en el cálculo de operaciones básicas, lo cual les hace avanzar con dificultad y lentitud. Uno de los alumnos presenta una desubicación elevada, ya que con la edad que tiene ya debería haber elegido o comprometerse a terminar alguna de las líneas educativas que se ofrecen (puede que todavía no haya definido sus gustos ni se haya definido como persona completamente y haya que esperar todavía). Otro de los alumnos presenta las características de un adolescente en sus etapas más tempranas, pero con la ventaja para Página 25 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS él de tener algunos de los conocimientos de los adultos. El resto de alumnos no presentan aspectos psicopedagógicos destacables. 3.3.2. Características psicosociales de los alumnos Las principales características psicosociales de los alumnos que se ha atendido durante la duración de las prácticas de este Master, son las siguientes: 1º ESO (Compensatoria): Un alumno presenta problemas familiares, ya que normalmente sus padres no le prestan la atención adecuada. En muchos de los casos, la familia de los alumnos presenta graves dificultades económicas con la madre y/o el padre en paro, lo cual hace plantearse al alumno cuestiones inadecuadas para su edad y provocando un comportamiento aversivo al estudio, al respeto de las normas de convivencia y a la vida en comunidad. El entorno familiar del que proviene otro de los alumnos es de etnia gitana, caracterizado por ser muy jerarquizado donde el papel del hombre es predominante al de la mujer. 2º ESO (A): Existe un alumno con ciertos problemas que no le permite seguir el desarrollo normal de las clases, aunque no presenta deficiencias cognitivas, es un año mayor que los demás y el grado de madurez que presenta es elevado. 2º ESO (B): Existen alumnos con trastornos antisociales, de los cuales además uno de ellos presenta en algunos casos un carácter negativista desafiante hacia el profesorado. También existe un alumno con indicios de inadaptación social, (que pueden ser debido a sus orígenes culturales y su entorno familiar). En otro de los casos, existen alumnos, presentan grandes habilidades psico-sociales que les capacitan para infundir un ambiente de control y respeto hacia ellas mismas por parte del resto de la clase. Página 26 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 1º Bachillerato Ciencias Sociales: Algunos de los alumnos se encuentran en situaciones familiares con dificultades económicas. En otro de los alumnos, sus padres han decidido darlo como caso perdido y actualmente está viviendo con su abuelo, lo cual motiva su despreocupación por los estudios y su falta de saber estar, ya que no tiene obligación de rendirle cuentas a nadie. El resto de alumnos no presentan características psicosociales especialmente destacables. 3.3.3. Condicionamientos socioculturales de los alumnos Las principales características socioculturales de los alumnos que se ha atendido durante la duración de las prácticas de este Master, son las siguientes: 1º ESO (Compensatoria): Algunos no se encuentran plenamente adaptados al entorno cultural que les rodea, en lo que atañe la relación con sus compañeros de diferentes etnias y procedencias. Por otra parte, otros alumnos presentan un exceso de control y protección por parte de su familia, que no le permite actuar con fluidez en el desarrollo habitual de las clases, lo cual, paradójicamente no le supone un impedimento para la consecución de los objetivos planteados para este curso, pero sí en su futuro desarrollo como persona íntegra. 2º ESO (A): Existen varios alumnos de origen árabe que no se encuentran adaptados completamente al entorno cultural que les rodea. Existen también algunos alumnos de diferentes orígenes culturales (sudamericano). Hay que hacer especial hincapié en el caso de tres chicas de origen árabe. Una de ellas, presenta una excesiva protección familiar y cultural que no le permite desarrollar una actuación fluida en las clases (quizá en clases más reducidas provocaríamos más su participación y con ello su progreso académico y cultural). En Página 27 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS otra de estas tres alumnas, coexistían deficiencias en el aspecto idiomático que ya ha superado, a la vez que sus procesos cognitivos y culturales, únicamente destacar que sus vestimentas siguen siendo muy semejantes a sus orígenes culturales, sin vista de una adaptación temprana. 2º ESO (B): En el caso de los alumnos de origen árabe actualmente presentan las inadaptaciones culturales propias de su edad, pero además se les añade un retraso en el desarrollo psico-evolutivo que no les permite realizar un desarrollo correcto en el centro. En el caso de tres alumnos de origen sudamericano, presentan otro tipo de inadaptación cultural diferente a los anteriores, ya que en este caso sí están totalmente integrados en la sociedad, pero todavía intentan imponer sus conductas tanto culturales como personales hacia los demás. 1º Bachillerato Ciencias Sociales: Los posibles condicionamientos socioculturales que podrían presentar los alumnos árabes y centroeuropeos presentes en la clase, por su procedencia, están completamente superados, incluso son capaces de analizar la realidad desde un punto de vista todavía más crítico y activo que los demás. 3.3.4. Principales diferencias individuales de los alumnos Las principales diferencias individuales presentes entre los alumnos de las clases a las que se ha podido acceder para hacer las prácticas de este Master de Profesorado, según los análisis personales que desde mi persona se han hecho y en colaboración con otros profesores del centro, divididas por cursos, son los siguientes: 1º ESO (Compensatoria): Se han detectado diferencias individuales de comportamiento entre los alumnos de etnia gitana y algún alumno de origen árabe, que influyen en el desarrollo normal de sus aprendizajes ya que cuando surge un conflicto Página 28 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS entre ellos deben estar en un aula aparte con el jefe de estudios. Existen a nivel general grandes diferencias en tanto origen cultural, educativo-formativo como social entre todos los alumnos de esta clase. 2º ESO (A): No se han detectado diferencias individuales especialmente reseñables entre los alumnos de este curso. Suelen formar diferentes grupos de amistades muy heterogéneos y variables a medida que pasan las clases en conjunto con los compañeros de otras clases, concretamente con 2ºESO B. Cabría reseñar, la diferencia existente entre los alumnos repetidores y ACNEs y el resto. 2º ESO (B): No se han detectado diferencias individuales especialmente reseñables entre los alumnos de este curso. Suelen formar diferentes grupos de amistades muy heterogéneos y variables a medida que pasan las clases en conjunto con los compañeros de otras clases, concretamente con 2ºESO A. Cabría reseñar, la diferencia existente entre los alumnos repetidores y ACNEs y el resto. 1º Bachillerato (Ciencias Sociales): No se han detectado diferencias individuales reseñables entre los alumnos de esta clase. Aunque se puede decir que no existe un grupo bien formado de compañeros y amistades debido a su reciente incorporación al centro como grupo y su diversidad de procedencias. Página 29 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.4 PROCESOS DE ENSEÑANZA-APRENDIZAJE EN LA INTERVENCIÓN EN EL AULA 3.4.1. Metodología empleada La metodología utilizada en el proceso de enseñanza-aprendizaje tanto para los alumnos de ESO como para los alumnos de Bachillerato, es de tipo constructivista cuando ha sido necesario y de tipo conductista en otros casos. Se han tenido en cuenta las habilidades cognitivas propias de cada etapa educativa y las potencialidades de cada alumno a partir de un análisis previo de los mismos y de las clases que se venían desarrollando hasta el momento de la intervención práctica en clase. Se tiene muy cuenta el aspecto tan reseñable que se dá en este centro sobre la atención a la diversidad tanto cultural como cognitiva, debido a las características propias del centro, detalladas en apartados anteriores, pero que a la hora de la verdad no se aplica correctamente. Se desarrollan actividades de ampliación para alumnos con altas capacidades intelectuales y cognitivas, así como actividades de apoyo para alumnos con deficiencias en el proceso de enseñanza o idiomáticas. El proceso de enseñanza-aprendizaje que se utiliza en el centro en algunos casos es de carácter paternalista, en el que el papel del profesor en muchas ocasiones desempeña funciones de orientador y corrector de faltas de comportamiento, con lo que se pierde cierta carga de contenidos. 3.4.2. Organización de actividades Además de las actividades propias de cada unidad didáctica en cada curso que se explican en los siguientes apartados, se realizan actividades en colaboración con otros Página 30 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS departamentos didácticos del centro para el desarrollo de la competencia lingüística (como es el proyecto de lectura – mate-cuentos, o la asistencia a jornadas de teatro del propio centro elaborado por el bachillerato de artes). También se realizan actividades de divulgación científica a través del nuevo periódico editado por el departamento de matemáticas del centro, en las que se indaga en temas científicos, astronómicos y normativos (ruidos-sonómetros) por parte de los alumnos de 4º ESO y 2º Bachillerato. Además, con los alumnos de compensatoria se realizan actividades de ampliación e interacción con el mundo físico y en el laboratorio de biología para el desarrollo de ciertas partes de las unidades didácticas. Por último se insta a participar en el concurso de primavera de matemáticas a los alumnos de ESO así como a los talleres de matemáticas de la Universidad de La Rioja. 3.5 UNIDAD DIDÁCTICA DE INTRODUCCIÓN A LAS DERIVADAS Y SUS APLICACIONES. 1º BACHILLERATO CIENCIAS SOCIALES 3.5.1. Introducción y contextualización La unidad didáctica que se va a desarrollar viene enmarcada en la programación didáctica de un Instituto de Educación Secundaria y Bachillerato de la zona urbana de Logroño. El centro está situado en el centro de la ciudad de Logroño, rodeado por espacios verdes. El acceso de los estudiantes al instituto suele ser a pie. En el centro educativo se imparten los cuatro cursos de ESO con una media de 2 grupos por curso académico más un grupo de adaptación curricular, para los tres Página 31 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS primeros cursos. Bachillerato de Ciencias Sociales y Artístico, así como una serie de grados medios y superiores en horarios diurno y vespertino. El ámbito socioeconómico del centro se caracteriza fundamentalmente por una gran diversidad de orígenes. En los niveles de la ESO se enmarca en un entorno urbano con una población trabajadora de clase media-baja con una alta tasa de desempleo y un pequeño sector de propietarios de negocios comerciales del mismo barrio. Por otro lado el alumnado de Bachillerato Artístico y grados superiores procede de diversos orígenes tanto sociales como económicos, los cuales son mayoría en el centro. El contexto cultural en el que se encuentra el instituto se caracteriza por una gran diversidad de alumnado desde alumnos de origen asiático y pakistaní hasta árabe y sudamericano, con un nivel de desarrollo educativo inferior a las exigencias del currículo. En algunos casos, existe déficit en el nivel lingüístico lo que conlleva una mayor dificultad en la transmisión del conocimiento. Se cuenta con un grupo heterogéneo en el que se intentará atender las necesidades individuales de cada miembro en la medida de lo posible. El ambiente escolar entre los alumnos es adecuado, sin que se haya detectado ningún tipo de problemática social relevante. La unidad didáctica a desarrollar está destinada a una clase de 1º Bachillerato de Ciencias Sociales. Dentro del bloque de análisis, la unidad didáctica de iniciación al cálculo de derivadas y sus aplicaciones se centrará en que los alumnos tengan oportunidades de investigar de manera sistemática las ideas del análisis (de manera informal), para profundizar en las estructuras conceptuales sobre las funciones de modo que las utilicen Página 32 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS para responder a cuestiones planteadas en el mundo real poniendo en práctica conceptos de optimización y representación. Los alumnos deben ser capaces de conocer y utilizar el concepto de derivada y su interpretación geométrica, utilizar con fluidez las reglas de derivación y su correlación, así como saber representar gráficas polinómicas y racionales de manera sencilla y definir sus características y hallar máximos y mínimos de las mismas para su utilización en la optimización. Inicialmente se repasará el concepto de límite (un enlace entre el concepto de limite y derivada) y las principales funciones vistas en la unidad didáctica anterior de manera que el aprendizaje sea más efectivo. Se introducirá el concepto de derivada en un punto y se relacionará con los conceptos de la asignatura de economía que se estén viendo en ese momento, para que el aprendizaje sea integrador, en la medida de lo posible. Además se realizarán dos trabajos individuales con ejercicios sobre utilización de las reglas de derivación que se entregarán al final de la unidad didáctica, si el devenir de las clases lo permite. 3.5.2. Objetivos Objetivos didácticos La unidad didáctica “Iniciación al cálculo de derivadas y sus aplicaciones” perteneciente al bloque de análisis de 1º curso de Bachillerato especialidad Ciencias Sociales tiene una serie de objetivos específicos, que se presentan a continuación: 1. Comprender el concepto de derivada de una función en un punto, así como su significado geométrico. Página 33 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2. Relacionar el análisis de ciertas situaciones reales con la interpretación de derivada. 3. Utilizar las reglas de derivación de funciones potenciales, exponenciales, logarítmicas y trigonométricas, así como las operaciones con las mismas. 4. Representar, identificar y analizar funciones polinómicas y racionales sencillas. Dominio, simetrías, cortes, asíntotas, monotonía, curvatura. 5. Hallar los máximos, mínimos y puntos de inflexión de una función. 6. Utilizar la optimización de funciones en casos reales. Objetivos generales presentes en la unidad didáctica Este apartado tiene como finalidad relacionar y comprobar que los objetivos específicos de la unidad didáctica forman parte de los objetivos generales que presenta el currículo de las matemáticas para el periodo educativo en el que se encuentra la unidad. Según el Decreto 45/2008 de 27 de Junio por el que se establece el currículo de bachillerato para la Comunidad Autónoma de La Rioja y su modificación según el Decreto 47/2010 de 19 de Agosto, la enseñanza de matemáticas tendrá una serie de objetivos generales, que se tendrán en cuenta en la consecución de este unidad didáctica. 3.5.3. Competencias La Ley Orgánica de Educación establece en el periodo de bachillerato una serie de competencias básicas, para este periodo, que son traspuestas casi íntegramente a la Comunidad Autónoma de La Rioja por el Decreto 45/2008 de 27 de Junio y su Página 34 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS modificación según el Decreto 47/2010 de 19 de Agosto, por el que se establece el currículo de Bachillerato para La Rioja. Competencia Lingüística (CL): Su finalidad es la de expresar oralmente y por escrito, utilizando el lenguaje matemático adecuado a su nivel, el procedimiento de resolución de un problema, conceptos, relaciones, representaciones gráficas y herramientas que ofrecen las derivadas en el bloque de análisis. Reconocer, analizar, describir y dibujar graficas polinómicas y racionales. Leer y disfrutar con la lectura histórica de la unidad didáctica y la introducción al tema. Competencia Social y Ciudadana (CSC): Su finalidad es la de trabajar en grupo, valorar y compartir puntos de vista diferentes para aprender a tomar decisiones en común. Competencia de Autonomía e Iniciativa Personal (CAIP): Su finalidad es la de poner en prácticas los diferentes métodos de resolución de derivadas aplicando conceptos anteriormente aprendidos, de manera personal e independiente. Adaptarse a utilizar distintas técnicas y métodos de resolución para mejorar el aprendizaje de los contenidos analíticos. Competencia Cultural y Artística (CCA): Su finalidad es la de valorar el contenido analítico como instrumento artístico y entender y dar una visión estética del mundo real afectado por el análisis. Competencia Matemática (CM): Su finalidad es la de utilizar el concepto de derivada para hallar la ecuación de la recta tangente a la curva en un punto y su pendiente, mediante la ecuación punto-pendiente. Utilizar las reglas de derivación de funciones exponenciales, potenciales, logarítmicas, trigonométricas e inversas trigonométricas, así como la representación de funciones polinómicas de orden superior Página 35 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS y funciones racionales. Hallar máximos y mínimos de las funciones con la utilización de las derivadas, para conocer el método de optimización. Competencia de Aprender a Aprender (CAA): Su finalidad es la de resolver problemas de derivación de funciones, escogiendo el procedimiento y la estrategia más adecuada en cada caso (mental, manual), y dar significado a las operaciones, métodos y resultados de acuerdo con el enunciado, usando instrumentos tradicionales (cuaderno y calculadora) o digitales (ordenador). Recoger y tratar información de diversas fuentes sobre funciones racionales y polinómicas analizando y sintetizando la información relevante. Competencia de Conocimiento e Interacción con el Mundo Físico (CCEMF): Su finalidad es la de aplicar conocimientos básicos sobre la derivación de funciones y la representación de las mismas para interpretar representaciones gráficas y realidades observables en el mundo natural. Competencia para el Tratamiento de la Información y la Competencia Digital (CTID): Su finalidad es la de utilizar el software adecuado para acelerar la interpretación de funciones y la visualización de las funciones derivadas, a partir de casos reales o ficticios. Valorar la utilidad de las TIC en el trabajo del análisis. Usar con soltura asistentes matemáticos y procesadores de texto para redactar, organizar, almacenar, imprimir y presentar un trabajo sobre análisis, aprovechando todas las herramientas disponibles en el centro. 3.5.4. Contenidos Contenidos conceptuales Tasa de variación media. Justificación analítica y geométrica. Derivada de una función. Justificación analítica y geométrica. Página 36 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Calculo de derivadas. Aplicación de las derivadas al estudio, representación gráfica de funciones sencillas y optimización de funciones. Contenidos procedimentales Utilización del vocabulario adecuado para interpretar y transmitir informaciones sobre funciones y derivadas. Expresión del concepto de derivada y comprensión geométrica. Utilización diestra de las reglas de derivación y capacidad de combinación de las mismas. Formulación y contextualización de problemas objeto de optimización. Utilización de programas informáticos para el dibujo de funciones y cálculo de sus derivadas. Contenidos actitudinales Valoración de los contenidos analíticos para transmitir informaciones precisas relativas al entorno. Incorporación al lenguaje cotidiano de los elementos analíticos y de los términos de medida para describir la realidad del mundo que nos rodea. Revisión sistemática del resultado de las medidas directas o indirectas, aceptándolas o rechazándolas según se adecuen o no a los valores esperados. Interés y gusto por la expresión verbal precisa de funciones y realidades del mundo que nos rodea. Confianza en las propias capacidades para percibir las ideas sobre funciones y derivadas, y resolver problemas analíticos. Página 37 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Perseverancia en la búsqueda de soluciones a los problemas analíticos y en la mejora de las ya encontradas. Interés y respeto por las estrategias y soluciones a problemas analíticos distintas a las propias. Sensibilidad y gusto por la realización sistemática y presentación cuidadosa y ordenada de trabajos analíticos. Perseverancia en el rigor y precisión en la escritura del lenguaje matemático en todas sus variantes. 3.5.5. Temas transversales Se expresaran aquellos valores personales y sociales que dictamine la Constitución española acorde la Ley Orgánica de Educación (LOE 2/2006) junto con el Decreto 45/2008 de 27 de Junio por el que se establece el currículo de bachillerato para la Comunidad Autónoma de La Rioja y su modificación según el Decreto 47/2010 de 19 de Agosto. Serán tratados en función de los objetivos y criterios de evaluación del área de matemáticas, en concreto para esta Unidad Didáctica que serán: o Educación Ambiental (EA). o Educación para la Paz (EP). o Educación el Consumidor (EC). o Educación para Igualdad de Oportunidades entre Sexos (EIOS). o Educación para la Salud (ES). o Educación Cívica y Moral (ECM). o Educación Vial (EV). Página 38 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.5.6. Metodología y estrategias de intervención La metodología utilizada es tanto de carácter individual como grupal. Siempre que se fomente el trabajo individual se tendrá presente las características que diferencian a nuestros alumnos, ofreciendo (en la medida de lo posible) una atención personalizada a cada uno de ellos para fomentar el aprendizaje significativo. La necesidad de educar para la convivencia y el respeto a los demás, así como las necesidades de la sociedad (en la que cada vez es mayor el número de empleos en los que se realizan trabajos en equipo), hacen cada vez más aconsejable proponer actividades y problemas que favorezcan el aprendizaje cooperativo en la clase de matemáticas. Debe inculcarse a los estudiantes el trabajo en equipo y la flexibilidad necesaria para que dicho trabajo se desarrolle con la mayor eficacia y en beneficio de todos. De esta forma, se obtendrán mayores niveles de colaboración y convivencia entre los miembros de toda la comunidad educativa, además de un aprendizaje más real y duradero. Con el aprendizaje cooperativo se pretende que los alumnos aprendan supervisados por el docente y argumenten las decisiones que van tomando en el transcurso de la tarea. Si utilizamos con frecuencia en nuestras aulas el aprendizaje cooperativo, nuestros alumnos mejorarán las estrategias de procesamiento de la información (suelen aprenderse las fórmulas de memoria sin conocer cómo se obtienen ni en que contextos de la vida diaria se aplican). Puesto que el alumno se ve obligado a aprender a hablar, ya no tendrá una actitud pasiva ante los problemas que planteemos en clase, se implicará en comprender la materia. Además, propicia un ambiente en el que cada alumno tiene expectativas positivas sobre los demás y en el que intenta ajustarse a esas expectativas que los demás tienen sobre él. Página 39 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Se utilizan las nuevas tecnologías mediante el uso de programas didácticos diseñados para la enseñanza de las matemáticas cuando la actividad lo requiera y trataremos de conectar lo que el alumno aprende en clase con la vida real para que puedan apreciar la utilidad de la materia. La estrategia de intervención con el alumnado que presente motivación, es de carácter cognitivista en la que los alumnos serán los propios constructores de su conocimiento, donde el profesor realizará la tarea de guía y permitirá que los alumnos lleguen a comprender los conceptos marcados en el currículo llegando a la hipotética de superarle, de manera que se produzca una aprendizaje significativo. Mientras que en el alumnado que presente desinterés por la materia se realiza una estrategia conductista en los casos en los que sea necesario introduciendo la materia nueva, mediante recursos disponibles en el aula permitiendo al alumnado adaptarse al suceder de la clase de la manera que más se le adecue desde su propia introspección. De esta manera se consigue atender a la diversidad en la medida que los recursos, el tiempo y la situación lo permitan. Se realiza una adaptación curricular para los alumnos que presentan una gran desmotivación debido al carácter finalista que tiene para ellos la estancia en clase durante el curso, ya que lo necesitan para presentarse a la prueba de acceso a grado medio, en la medida de lo posible. En cada clase se procede mediante preguntas iniciales sobre situaciones reales propias de los alumnos, de modo que se involucren en el acontecer del aula mediante las cuales se introducirán los conceptos nuevos de una manera intuitiva, para que después los apliquen en los ejercicios propuestos. Página 40 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Las actividades propuestas están relacionadas con la unidad didáctica correspondiente que estén en ese momento recibiendo en la asignatura de economía, de manera que la visión de los alumnos sobre el concepto de derivación sea más amplia e integradora, así como la utilización de términos y vocabulario en el Inglés y Francés en tono de incentivo. ______________________________________________________________________ La metodología a seguir para la iniciación de la unidad didáctica será de tipo constructivista, en función de la aptitud de los alumnos en cada momento de la clase, de manera que hagan suyo el concepto de derivada para pasar a una metodología conductista durante la explicación de las diferentes reglas de derivación. Por último, se desarrollaran actividades de ampliación que fomenten el uso e investigación de las derivadas individualmente, se podrá contemplar la realización de algún tipo de trabajo sencillo de manera individual tanto previo como final para comprobar el nivel de adecuación e interés de la unidad didáctica para los alumnos. Se realizarán dos primeras clases de relación con los contenidos históricos de la unidad didáctica en concreto, relacionándolos con la época actual, es decir se promoverá en clase a los alumnos, intentar llegar a las teorías que finalmente se conseguirán a través de los medios y conceptos que se tenían en esa época, como medio de motivación. Se buscarán problemas de la vida diaria en los que se encuentre de aplicación el concepto de derivada para intentar hallar una resolución hipotética sin disponer de los conocimientos adecuados de derivación. Se planteará el concepto de derivada proveniente de la idea de límite con la ayuda de software matemático, de manera que sea más intuitiva mediante una aplicación dinámica, del concepto de derivada. Página 41 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Finalmente se realizaran una serie de ejercicios en la pizarra con el ánimo de que los alumnos cojan soltura con el concepto de derivada, de manera participativa lanzando preguntas continuas a la clase. Por último se procederá a una evaluación parcial de los conceptos aprendidos en cada hora de clase. Se realizará un listado de las diferentes reglas de derivación directa enlazando con los conocimientos previos sobre potencias, trigonometría, exponenciales, logaritmos y racionales ordenados por nivel de complejidad. A medida que avancen las clases se realizarán una serie de ejercicios de tipo conductista, hasta que cojan soltura con todas las reglas de derivación directa. Al finalizar, este parte de la unidad didáctica se realizarán comentarios sobre las diferentes características que presentan gráficas de la vida real, de modo que vean la utilidad de las mismas y otros posibles métodos de resolución, a modo de introducción de la representación de gráficas. Por último, se realizarán ejercicios de interpretación de graficas polinómicas primero y racionales después por orden de complejidad, llegando al análisis de la curvatura y de asíntotas oblicuas. Al final de la unidad se introducir ejercicios de optimización de funciones tal y como marca el currículo relacionados con el mundo de la economía, primero de manera intuitiva relacionando el concepto de monotonía y de puntos críticos visto en la representación de gráficas para poder pasar de manera más conexa a realizar ejercicios más complicados en los que crear la función a derivar a partir de una serie de datos de partida. Finalmente se realizará una clase de repaso de contenidos y puntos clase de la unidad didáctica a modo de cierre de la misma, con los correspondientes comentarios por parte de los alumnos. Página 42 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.5.7. Actividades. (Ver Anexo 1) 3.5.8. Recursos y materiales de apoyo a la docencia Los recursos que se van a necesitar para el desarrollo de la presente unidad didáctica son a nivel general los que aparecen detallados en el Anexo 2 de este documento. Además, se van a dividir en tres grupos básicos, complementarios y auxiliares. Dentro de cada uno de ellos se especifica el tipo de recurso que es y el valor didáctico que va a aportar en esta UD. (Ver Anexo 3). 3.5.9. Temporalización Se disponen de 4 horas lectivas a la semana para la asignatura de matemáticas (lunes, martes, miércoles y jueves). Marzo 2014 DÍAS 6-03 10-03 11-03 12-03 13-03 17-03 18-03 19-03 20-03 SESIONES 1º 2º 3º 4º 5º 6º 7º 8º 9º Marzo-Abril 2014 DÍAS 24-03 25-03 26-03 27-03 31-03 01-04 02-04 03-04 07-04 SESIONES 10º 11º 12º 13º 14º 15º 16º 17º 18º Se ha dividido la docencia de esta unidad didáctica en 3 partes de contenidos: 1. Introducción histórica del origen de las derivadas y su utilidad en la actualidad. Tasa de variación media, definición de derivada y sus correspondientes interpretaciones geométricas. Página 43 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2. Obtención de las reglas de derivación directa a modo de introducción. Aprendizaje memorístico y a base de trabajo de las reglas de derivación por partes. Operaciones básicas, potenciales, exponenciales, logarítmicas, trigonométricas e inversas trigonométricas. Por último la regla de la cadena. 3. Introducción de gráficas reales e interpretación de viva voz de todas las características fundamentales de manera intuitiva. Introducción de los pasos a seguir para la representación de una gráfica polinómica o racional. Optimización de problemas relacionados con la economía. Durante toda la unidad didáctica los alumnos deberán copiar el contenido teórico en los cuadernos personales, a partir de la lección del profesor y del contenido del libro. Al final de la unidad didáctica se ofrecerá un resumen de conceptos y contenido teórico de la unidad on-line. El desarrollo de cada sesión será como sigue a continuación (Ver Anexo 4). 3.5.10. Evaluación La evaluación se realiza de manera continua con un examen al final de unidad didáctica. Además se ha programado realizar un examen de bloque para la recuperación de alumnos los que tengan alguna parte o todo el bloque de análisis suspenso. Se realizará una evaluación de la participación en clase de cada día. Se aconsejará la realización de una serie de trabajos on-line o de modo manuscrito, que los alumnos tendrán que entregar al cabo de la unidad didáctica. Criterios de evaluación Uno de los criterios de evaluación que marca el currículo de Bachillerato en Matemáticas de Ciencias Sociales, esta específicamente centrado en este bloque. Y es Página 44 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS que los alumnos deben ser capaces de identificar las funciones habituales (lineales, afines, cuadráticas, exponenciales, logarítmicas, trigonométricas y racionales sencillas) dadas través de enunciados, tablas o expresiones algebraicas, obtener sus gráficas para analizar y aplicar sus características al estudio de fenómenos económicos, sociales, naturales, científicos y tecnológicos que se ajusten a ellas, valorando la importancia de la selección de los ejes, unidades, dominio y escalas. Este criterio pretende evaluar la capacidad para interpretar y aplicar a situaciones del mundo natural, geométrico y tecnológico, la información suministrada por el estudio de las funciones. Particularmente, se pretende comprobar la capacidad de traducir los resultados del análisis al contexto del fenómeno, estático o dinámico, y extraer conclusiones sobre su comportamiento local o global. Además de estos criterios de evaluación definidos por el currículo, se tendrán en cuenta los siguientes aspectos: Expresión oral y por escrito de los conceptos, procedimientos y terminología propios de la derivación. Asimilación del concepto de tasa de variación media y relación con la pendiente de una recta y la definición de derivada. Aplicación de la definición de derivada y de su aplicación para hallar la ecuación de la recta tangente a una curva en un punto. Identificación del tipo de derivada a utilizar. Cálculo y simplificación de resultados. Interpretación geométrica de resultados. Relación entre reglas de derivación. Asimilación del procedimiento de optimización y su relación con la búsqueda de puntos críticos en la representación de funciones. Página 45 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Representación de funciones racionales y polinómicas sencillas. Ordenación de resultados e interpretación geométrica de los mismos. Dominio, simetrías, cortes, asíntotas (oblicuas varios procedimientos), monotonía y curvatura. Explicación y razonamiento de resultados. Instrumentos de evaluación La observación diaria de la participación en clase de alumno. Comportamiento en clase. Utilización de la página web y de los recursos subidos a la misma. Realización de trabajos entregables al final de la unidad de manera escrita e individual. Realización de ejercicios diarios para el seguimiento de la asignatura. Prueba de calificación final de la unidad didáctica. NOTA: Se utilizará un recurso informático, del tipo aplicación web con su correspondiente herramienta de fácil manejo, para la recogida eficiente y rápida de todos estos en el comienzo de cada clase. Momentos de evaluación Se llevará a cabo una evaluación continua de la participación y de la asistencia en clase, así como de los ejercicios realizados día a día y de la utilización de la página web. Evaluación inicial: Se llevará a cabo al principio de cada sección de contenidos de esta unidad didáctica en el momento de la introducción de actividades de motivación. El profesor realizará una serie de cuestiones a los alumnos teniendo en cuenta sus intereses a priori, Página 46 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS y sus procedencias, de manera que se dote sentido real a los conceptos que posteriormente se impartirán. Evaluación formativa: Tiene como objetivo ajustar la ayuda pedagógica del alumno a lo largo del proceso de enseñanza-aprendizaje. Esta evaluación se realizará mediante la observación en clase, la elaboración y corrección de tareas durante la unidad didáctica y la proposición de preguntas tanto del profesor a los alumnos como de estos hacia el profesor. Evaluación final: Con el fin de conocer si se han obtenido los objetivos, el profesor realizará un examen al final de la unidad. La recogida de cuaderno al final de cada unidad didáctica también será evaluada en la nota final. La forma de evaluar el examen será como se indica a continuación: El examen se evaluar sobre 100 puntos. En cada ejercicio se tendrá en cuenta de la manera conveniente la identificación del tipo de ejercicio, las herramientas a utilizar, el cálculo realizado, el resultado obtenido y la justificación y explicación de los resultados finales. Durante toda la corrección se tendrá en cuenta como criterio común la limpieza y el rigor en la escritura de los datos y las fórmulas. La forma de evaluar los ejercicios individuales, será como se indica a continuación: Se tendrá en cuenta la identificación del tipo de ejercicio, las herramientas a utilizar, el cálculo realizado, el resultado y su explicación, así como la limpieza y el rigor en la presentación escrita. Si la fecha de entrega no Página 47 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS está dentro del plazo previsto, se descontará nota con el cociente de reducción correspondiente. La forma de evaluar toda la unidad didáctica, será como indica la siguiente tabla: La nota final se compondrá en un 85% de la nota del examen, de un 5% de la nota suma entre comportamiento, participación y asistencia, de un 5% de la nota suma entre utilización de la página web, ejercicios y el trabajo individual. En el caso de que la nota final del examen sea muy alta y la del resto muy baja, se realizará el correspondiente cálculo con el cociente ponderación que se estime. Para la recogida de todas las notas se utilizará una hoja cálculo adaptada a las necesidades del profesor con los datos de todos los alumnos, facilitados por el centro. Página 48 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.6 OTRAS ACTIVIDADES REALIZADAS Preparación de ejercicios y clases con material virtual para alumnos de ESO. Preparación y resolución de ejercicios para Bachillerato y como material de apoyo al estudio, tanto de manera tradicional como virtual. Preparación de videos documentales para debatir sobre sociedad en clases de Atención Educativa. Clases de apoyo en aula de convivencia, con material de apoyo al estudio y atención a las necesidades diarias de cada alumno conflictivo que acudía. Guardia en la biblioteca. Colgada de carteles sobre talleres de matemáticas de la Universidad de La Rioja. Reuniones de departamento semanales. Posibilidad de acudir a juntas de evaluación (a la que al final no se ha acudido). Concurso de primavera para alumnos de ESO. Apoyo en la redacción del periódico editado por el departamento de matemáticas. Apoyo en la preparación de actividades de alumnos con la asignatura de matemáticas pendiente. Apoyo en la preparación del examen de alumnos con la asignatura de matemáticas pendiente. Realización supervisada del examen de tarde para bachillerato. Apoyo en la preparación de exámenes para un grupo de adaptación curricular y dos grupos de 2º ESO. Visualización en persona de otras clases como oyente de otras especialidades, por iniciativa propia del profesorado. Aconsejar la utilización de otros recursos y propuestas educativas a profesores del departamento de filosofía, latín, biología y música en relación con las matemáticas. Página 49 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.7 REFLEXIONES SOBRE LAS PRÁCTICAS 3.7.1. Sobre lo acontecido en el instituto Desde el comienzo de las prácticas, allá por el mes de Diciembre momento en que acudí al instituto a presentarme como futuro profesor en prácticas, hasta los últimos días en el centro, todo los agentes educativos del centro han sido muy acogedores y enriquecedores para mi persona. Todos ellos han estado muy pendientes de mí en el momento que les he necesitado y han estado abiertos a nuevas propuestas para cualquier desarrollo educativo del centro. Desde el departamento didáctico de matemáticas se me ha acogido con gran entusiasmo y en todo momento se me ha explicado el acontecer diario del centro, de las clases, de las actividades extraescolares y de las propuestas educativas del entorno del centro. El ambiente desde mi punto de vista ha sido inmejorable y me ha permitido desplegar todas las capacidades y conocimientos de los que dispongo, así como descubrir otros que pensaba no tener. La relación con los alumnos ha sido la esperada, mi antigua experiencia escolar en el mismo instituto como alumno me ha facilitado la comprensión del entorno sociocultural y psicosocial del centro en gran manera. De todos modos, la relación con los alumnos ha sido próspera y gratificante tanto en cuanto a conocimientos desarrollados con ellos como en la relación personal con los mismos, de la cual espero les quede algo en un futuro. Página 50 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.7.2. Sobre la memoria de prácticas Desde mi punto de vista, que en los centros donde existe un mayor porcentaje de población inmigrante que autóctona se fomente el uso de la lengua extranjera como es Francés e Inglés es un error administrativo que debería tenerse en cuenta, o al menos reflexionar más sobre él, ya que se da una aculturación del entorno social del centro que no se corresponde con la normalidad del mismo. El apoyo idiomático que se le da a este tipo de alumnado debería estar contemplado en el currículo de una manera específica de modo que se realicen actividades de interacción entre los diversos idiomas hablados y desarrollados por los alumnos de manera independiente, debido a sus orígenes, de modo que el aprendizaje y motivación del resto de alumnos sea diferente al actual y desde mi punto de vista mucho más productivo. Sin dejar de lado por ello los idiomas tradicionalmente extranjeros con tanta influencia en el mundo de hoy en día como son Francés, Inglés y Alemán. El tipo de evaluación que se realiza comúnmente para los alumnos con adaptación curricular, desde mi punto de vista personal no es el más correcto, además de que se pierden posibles alumnos con altas capacidades o capacidades sin identificar hasta el día de hoy, que podrían desarrollar un progreso educativo equivalente o mejor al del resto de sus compañeros. Por ello, debería existir la posibilidad de dotar al profesorado de más recursos, sobretodo de carácter temporal, para poder preparar pruebas que realmente evalúen las capacidades de los alumnos con adaptación curricular, ya que en muchos de los casos presentan aptitudes muy válidas para su desarrollo como personas, pero que normalmente no se encuentran reflejadas en los currículos oficiales. Página 51 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Respecto a la relación que hoy se tiene con las familias desde los centros de educación, se hace evidente que no da los resultados que se pretenden en su conjunto, ya que en muchos casos las familias no participan de la vida de los centros y únicamente asisten por obligación y de manera excepcional. En algunas familias los padres presentan también necesidades educativas grandes, ya sea idiomáticas o de conocimientos, que el centro podría satisfacer, en colaboración con sus hijos, mediante actividades conjuntas, haciéndoles más participes de la vida de sus hijos en los centros. Del mismo modo, a padres sin estas necesidades, podrían despertar en sus hijos nuevos intereses que redunden en un mejor progreso académico y personal de los mismos. Aquí debería de haber en tono aperturista un punto que trate sobre la relación con los padres en el propio devenir de muchos de los alumnos, cuyas adaptaciones curriculares son en algunos casos ineficaces, donde posiblemente la educación que se les pueda ofrecer a los padres podría ser un buen punto de partida. Página 52 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 3.7.3. Sobre la situación actual y conclusión final Teniendo en cuenta el momento en el que nos encontramos, en el que nos estamos cuestionando todo lo que hemos heredado de nuestras generaciones anteriores, para intentar construir un futuro acorde a nuestras expectativas, necesidades y potencialidades futuras tanto como seres humanos como, como seres que desarrollan el conocimiento y el progreso científico, sería bueno plantearse la posibilidad de cambiar parte de la formación que se imparte en las universidades a nivel general dotándolas a todas ellas la posibilidad de realizar determinadas asignaturas (optativas) que se preocupen por la enseñanza de la especialidad en concreto, de modo que se asegure la transmisión de conocimientos entre generaciones y así la mejora de la calidad educativa estructuralmente. Otra posibilidad, es desarrollar carreras profesional en el nivel universitario de cada especialidad pero orientadas únicamente al desarrollo de la profesión como profesor, al igual que existe ya en países sudamericanos como Argentina donde podemos encontrar carreras como Profesorado de Matemáticas con la misma carga de créditos que una carrera normal. Por otro lado, uno de los aspectos que considero que actualmente no está correctamente regulado si de verdad se le pretende dar un sentido tan fundamental a nuestra educación, es el aspecto económico laboral de la realización de estas prácticas. Que mejor manera de fomentar la formación de los profesores y la mejora con ello de la educación, que una correcta regulación laboral de estas prácticas, que actualmente no están económicamente reconocidas, cuando realmente es un trabajo que se desempeña con gran entrega, profesionalidad y responsabilidad, tanto por parte del alumno como parte del tutor correspondiente. Página 53 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Todo lo acontecido durante este periodo de prácticas y debido a la situación actual, me lleva a pensar lo siguiente. Muchas de las consecuencias que a día de hoy vivimos en nuestro entorno, ya sea relacionado con la justicia, la política, la cultura, la sanidad, la ideología, el comportamiento como ciudadanos, el entorno y situación laborales, son consecuencia directa de la educación que recibimos tanto positiva como negativamente. Es muy necesario hacer una tarea de revisión conjunta de nuestras conductas, nuestros sentimientos y necesidades particulares de manera individual que nos permitan llegar y alcanzar acuerdos comunes que logren llegar a un acuerdo común y perdurable en materia de educación que nos haga progresar científica, social y económicamente. A modo de conclusión de este periodo de prácticas que he desarrollado en el Instituto de Educación Secundaria IES Batalla de Clavijo de La Rioja, considero que la tarea de profesor es de las más dignas que un ser humano puede realizar a lo largo de su vida. Todos deberíamos entender esta profesión y lo que conlleva y hacer un esfuerzo en el día a día de cada uno por intentar enseñar cosas que otros no saben, por mucho que nos suponga económica o culturalmente, de modo que evolucionemos hacia un futuro mejor y que todos podamos entender de la mejor manera. Como dicen diferentes teorías psicológicas el enseñar es una capacidad innata del ser humano, pero que muchas veces cortamos por intereses que no son propios del ser humano, pero que se nos hacen necesarias para sobrevivir. Página 54 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4. PROYECTO DE INNOVACIÓN E INVESTIGACIÓN EDUCATIVA 4.1. INTRODUCCIÓN Y CONTEXTUALIZACIÓN El marco general de este proyecto de investigación se centra en la utilización de la teoría de inteligencias múltiples propuesta por Howard Gardner en el año 1983, para mejorar el aprendizaje significativo de los alumnos en las clases de matemáticas de secundaria. Las características psico-pedagógicas que presentan los alumnos de hoy en día nada tienen que ver con las de hace tan solo dos décadas. La irrupción de la revolución digital ha modificado nuestra manera de ver la realidad, de interpretarla, de reflexionar sobre ella, de relacionarnos con los demás, de actuar, de opinar, de trabajar y en definitiva de vivir. Nos tenemos que dar cuenta que los que son hoy y mañana alumnos han nacido ya con los ordenadores y los “smartphones” y no entienden una vida apartada de los mismos. Por otro lado, el cambio que ha producido las tecnologías en el ámbito del trabajo, la empresa y la economía ha producido una modificación en las hoy en día llamadas competencias requeridas en los futuros trabajadores y empleadores, tanto en el ámbito lingüístico (relaciones internacionales), social (filosofías de trabajo LEAN, caracterizadas por su humanidad y eficiencia), digital, lógica, natural (respeto por el medio-ambiente), personal, ha supuesto un cambio de paradigma de 180º (por ejemplo, en la producción industrial mediante impresoras 3D, la nueva moneda digital BITCOIN o la aplicación de técnicas como el aprendizaje por proyectos en la educación). Hace unos pocos años no se tenían en cuenta todos estos aspectos y puede Página 55 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS que a causa de la crisis en la que nos encontramos (o no), nos haya hecho darnos cuenta de que es necesario cambiar muchas cosas de nuestra realidad. La relación que hoy se da entre las competencias establecidas en los currículos de educación y la actividad diaria de una persona tanto en el ámbito personal como laboral, muchas veces no es la más eficiente ya que el desarrollo de las personas como he dicho anteriormente ha cambiado de paradigma, mientras que el desarrollo de los currículos educativos sigue enmarcado en la funcionalidad de las personas y la educación integra de cada una de ellas. Los alumnos hoy en día tienen una gran capacidad de adaptación al entorno y el acceso a las redes sociales y a internet les permite buscar y entender nuevos conocimientos más rápidamente y relacionarlos entre sí para crear otros nuevos de su propia mano. Según las recientes pruebas PISA realizadas en el año 2012 para la evaluación de la competencia matemática (tanto digital como escrita) en alumnos de 15 años españoles, han dejado en relieve unos resultados aunque no malos si por debajo de la media de la OCDE (477 puntos/500 puntos), lo cual nos debiera decir que algo hay que cambiar en el contexto de las matemáticas. Pero hay que profundizar un poco más en esta prueba para saber exactamente lo que está ocurriendo en el aprendizaje de las matemáticas por parte de alumnos de secundaria en España, ya que el número de alumnos encuestados, no tiene porqué representar la gran diversidad educativa de España, aunque estemos enmarcados dentro de los parámetros de la OCDE. Por ello, se hace necesario un análisis más profundo sobre esta cuestión y plantearse otras preguntas. Página 56 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Los últimos avances en neuropsicología, permiten entender mejor nuestro cerebro, su estructura genética, las relaciones que existen entre sus componentes y las interacciones sociales. Las diferentes etapas de crecimiento de nuestro cerebro y sus capacidades innatas, no son perceptibles a simple vista y para producir un desarrollo óptimo del cerebro de nuestros alumnos es necesario provocar unos entornos de aprendizaje adecuados que permitan una interconexión de conocimientos, realidades y entorno social de cada alumno. Además los procesos mentales y habilidades que intervienen en las clases de matemáticas requieren en una gran medida de provocar estos nuevos entornos de aprendizaje. Desde otro punto de vista, se puede plantear que el periodo y el tiempo de aprendizaje establecido por las administraciones para realizar los estudios tanto básicos como superiores, sigue siendo a grandes rasgos el mismo, (educación primaria 6-8 años, educación secundaria 4-6 años y educación superior 3-6 años), y que a medida que han pasado los años sobre todo desde mediados del siglo XX, la esperanza de vida ha crecido alrededor de unos 30 años, por lo que cabe plantearse si los periodos de aprendizaje deberían ser más amplios y relajados, además para hacer ver a la persona que el proceso de aprendizaje es algo continuo en nuestra vida “la educación hay que verla como un proceso continuo a lo largo de tu vida, ya que si dejamos de aprender seremos personas disfuncionales en algún momento de nuestra vida, ya que no seremos capaces de adaptarnos a las necesidades del momento” Howard Gardner. También es cierto y es necesario tener en cuenta que el avance científico de los últimos años ha sido mucho mayor que en todo el siglo XX debido a los avances tecnológicos y que por ello hay mucha más cantidad de conductos para aprender y además son más profundos y entrelazados. Página 57 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Muchas veces el avance de la sociedad no es detectado o no es posible de ser asimilado por los contenidos curriculares, debido a la gran carga existente y el reducido tiempo de aprendizaje, lo cual produce en los alumnos desmotivación por el estudio. La cada vez mayor atención a la diversidad que requieren nuestros alumnos debido a su gran diversidad de procedencias y a la mayor aun diversidad de inquietudes y talentos (debido al progreso científico y al gran abanico de posibilidades que este ofrece), requiere una educación personalizada, que hoy en día no se ve satisfecha y que únicamente queda reflejada en papel escrito. 4.2. JUSTIFICACIÓN-MOTIVACIÓN DEL PROYECTO Y OBJETIVO Las primeras preguntas que se me han planteado a partir de mi experiencia como docente en prácticas en un centro de educación secundaria de la Comunidad de La Rioja son las siguientes: ¿Hasta dónde, en el nivel de secundaria, se le enseña al alumno a comprender la realidad? ¿En qué grado, la educación secundaria activa el perfil intelectual más adecuado en cada alumno, para que los alumnos puedan aprender y demostrar su aprendizaje de una manera que tenga sentido para ellos? ¿Cuál es la concepción de inteligencia que se presenta en alumnos riojanos de secundaria y cuál es el papel que éstos atribuyen a la escuela en el desarrollo de la misma? Página 58 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS ¿En qué medida el currículo formal y el currículo real que se aplican en las secundarias públicas de la Comunidad Autónoma de La Rioja coadyuvan al desarrollo del espectro intelectual entre los estudiantes? ¿Cuál es la concepción de inteligencia que presenta el profesor riojano de Educación Secundaria y que estrategias implementa para desarrollarla en los alumnos a través de la intervención pedagógica? ¿Cuáles son las metodologías para que dicha participación favorezca el desarrollo del espectro intelectual en adolescentes de secundaria? La percepción que muchos alumnos tienen de las clases de matemáticas, en concreto, es que son frías y distantes a la realidad cuando en casi todas las ocasiones tienen conexión directa con todos los ámbitos sociales, industriales, tecnológicos, económicos, laborales y científicos. Los estudiantes (en esta época de la gratificación instantánea) suelen preguntar "¿Y eso para que me sirve?", cada vez que los profesores abordan un tópico nuevo. Podríamos contestarles que algún día les servirá para entender y responder mejor a algunas de las muchas crisis que vendrán. Pero no será una respuesta que los deje satisfechos ya que es difícil pretender que los estudiantes de hoy estén desde ahora preocupados por las crisis del 2043. Lo que el estudiante quiere saber es para que le sirve lo que está aprendiendo no mañana ni dentro de una semana sino hoy y ahora. Por ello, el profesor debe anticiparse a que el alumno se cuestione tal pregunta, y tiene que hacer las matemáticas más relevantes y cercanas a los intereses de los alumnos y hacerles interesarse por ellas. Y además no solo ofrecer una serie de procedimientos establecidos en los currículos porque para ello ya están las tecnologías que todo lo implementan, sino también enseñar a comprender los procedimientos, cuestionarlos, abstraerlos y adaptarlos según las necesidades. Página 59 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS También hay que darse cuenta de que al igual que el profesor Howard Gardner se dio cuenta de que existen diferentes inteligencias generales, en matemáticas también hay diferentes inteligencias. Hay alumnos y profesores que están mejor dotados y preparados para pensar geométricamente, otros tienen las destrezas numéricas más desarrolladas, la fortaleza de alguno es para armar y desarmar rompecabezas, escabullirse por laberintos, mientras que no faltarán los que disfrutan con la estadísticas y todas sus variantes. Descubrir en cada estudiante sus fortalezas y sus intereses particulares, que suelen complementarse, es una manera de tener más probabilidades de acertar a la hora de decidir cómo abordar el trabajo en el aula. Pero ello significa también, abandonar la clase magistral tradicional como único recurso para enseñar y optar más bien por una especie de laboratorio de matemáticas donde distintos grupos de estudiantes trabajan en diversos experimentos matemáticos, según sus intereses, sus afinidades, sus habilidades y necesidades de aprendizaje. La matemática es una ciencia experimental que progresa fruto de la observación, imaginación y experimentación, formulando hipótesis sobre problemas que está investigando y procurando por distintos medios ponerlos a prueba, comprobándolos y refutándolos a base de experimentos. Ese ambiente de experimentación es el que hay que intentar reproducir en el salón de clase, fomentando, como ocurre en la vida real, el trabajo en equipo y algo de competencia sana entre los mismos. Este trabajo en equipos permite, además, que las distintas inteligencias matemáticas de sus miembros se complementen en la solución exitosa de un problema o el desarrollo de un proyecto ya que, por lo general, un mismo problema o proyecto, bien escogido, hace uso de todas ellas. En el proceso los estudiantes aprenden los unos de los otros mucho más de lo que aprenderían del profesor que copia y resuelve problemas en el tablero para que los Página 60 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS estudiantes los copien igual en sus cuadernos y, después de memorizados, en la hoja de la previa. Implementar todo ello en una clase de manera que se produzca un aprendizaje significativo y no den interrupciones continuas en el desarrollo de una clase no es algo fácil, pero la oportunidad que ofrecen las nuevas tecnologías y las nuevas capacidades de los alumnos hacia el aprendizaje de las matemáticas, no podemos desaprovecharla por mucho esfuerzo que nos conlleve. Los procesos mentales que intervienen en cada una de las inteligencias matemáticas como son la abstracción, la síntesis, el análisis, el cálculo, la lógica, la visión espacial, la memoria, son los que el profesor de matemáticas debe desarrollar en sus alumnos y tener un “feedback” continuo de cuál es el grado de desarrollo de cada uno de ellos en cada alumno. Por otro lado, el planteamiento curricular que se hace de la enseñanza por asignaturas no permite un desarrollo completo y óptimo de todas las inteligencias, talentos y capacidades de nuestros alumnos ya que aísla en cajones estancos los contenidos aprendidos en cada una de las asignaturas, por ello se hace necesaria una revisión completa de los mismos, en la que en lugar de asignaturas con contenidos al uso, deberán ser clases por tipos de inteligencias a desarrollar en las que mezclar diversos contenidos. El planteamiento actual de la enseñanza no aprovecha de una forma eficiente la multiplicidad de talentos e inteligencias que pueden tener los alumnos. Las mezclas culturales que se están dando en muchos centros españoles pueden producir una serie de conocimientos nuevos que se están tirando al traste por la falta de recursos y en muchas Página 61 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS ocasiones se están abriendo o gracias al profesor implicado de turno o gracias al acceso a las redes sociales y a internet y no a la educación ofrecida en los centros. Por ello, el planteamiento de las clases en este caso de matemáticas en la enseñanza, debe hacerse desde la teoría de las inteligencias múltiples, para aprovechar todas las potencialidades que los alumnos, los recursos y los avances científicos nos brindan en la actualidad, para forjar personas integras con fuertes capacidades para su futuro. Por lo que el objetivo de este trabajo de innovación docente en el aula de matemáticas se centra en el desarrollo de clases de matemáticas a través de la teoría de las inteligencias múltiples desarrollada por Howard Gardner. 4.3. MARCO TEÓRICO VS FUNDAMENTACIÓN La teoría de las inteligencias múltiples es un modelo propuesto en el libro “Estructuras de la mente” de 1983 de Howard Gardner en el que dice que la inteligencia no es vista como algo unitario que agrupa diferentes capacidades específicas con distinto nivel de generalidad, sino como un conjunto de inteligencias múltiples, distintas y semi-independientes. Gardner define la inteligencia como la “capacidad mental de resolver problemas y/o elaborar productos que sean valiosos en una o más culturas”. Primero, amplía el campo de lo que es la inteligencia y plantea que la brillantez académica no lo es todo. A la hora de desenvolverse en la vida no basta con tener un gran expediente académico. Hay gente de gran capacidad intelectual pero incapaz de, por ejemplo, elegir bien a sus amigos; por el contrario, hay gente menos brillante en el colegio que triunfa en el mundo de los negocios o en su vida privada. Triunfar en los Página 62 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS negocios, o en los deportes, requiere ser inteligente, pero en cada campo se utiliza un tipo de inteligencia distinto. Ni mejor ni peor, pero sí distinto. Dicho de otro modo: Einstein no es más ni menos inteligente que Michael Jordan, simplemente sus inteligencias pertenecen a campos diferentes. Segundo, y no menos importante, Gardner define la inteligencia como una habilidad. Hasta hace muy poco tiempo la inteligencia se consideraba algo solamente innato. Se nacía inteligente o no, y la educación no podía cambiar ese hecho (en el sentido de aprovechar más o menos la parte innata). Tanto es así, que, en épocas muy próximas, a los deficientes psíquicos no se les educaba, porque se consideraba que era un esfuerzo inútil, cuando en realidad existe tanto la parte innata (genética) como la parte adquirida (mayor o menor provecho de la parte innata a lo largo de la vida), como ya se puede ver en las teorías constructivistas de aprendizaje, pero que no termina de entroncar bien con el devenir del día a día de las clases con los alumnos actualmente, debido a la misma disquisición que supone entender todavía la teoría de las inteligencias múltiples. Según el análisis de las ocho inteligencias, todos los seres humanos son capaces de conocer el mundo de ocho modos diferentes, a través del lenguaje, del análisis lógico-matemático, de la representación espacial, del pensamiento musical, del uso del cuerpo para resolver problemas o hacer cosas, de una comprensión de los demás individuos, de una comprensión de nosotros mismos y de una comprensión para percibir las relaciones que existen entre varias especies o grupos de objetos y personas. Donde los individuos se diferencian, es, en la intensidad de estas inteligencias y en las formas en que se recurre a esas mismas y se les combina para llevar a cabo diferentes labores, para solucionar diversos problemas y progresar en distintos ámbitos. Página 63 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Lógicamente cada inteligencia está compuesta por determinados subconjuntos lo cual explica la inabarcable biodiversidad incluso en este tema. La educación actual, por tanto, no es que se centre realmente en las dos primeras inteligencias, sino que se centran en determinados subconjuntos de dichas inteligencias y además no llega a trabajarlos de manera interdisciplinar. Las personas aprenden, representan y utilizan el saber de muchos y diferentes modos. Estas diferencias desafían al sistema educativo que supone que todo el mundo puede aprender las mismas materias del mismo modo y que basta con una medida uniforme y universal para poner a prueba el aprendizaje de los alumnos. Esto conlleva a crear supuestas jerarquías, cuando cada persona tiene un tipo de combinación de las ocho (o veremos si hay más) inteligencias distinto. A todo esto también se hace necesario añadir, que además de las ocho inteligencias propuestas por Gardner, la creatividad es un constructo que se encuentra impregnado en esas ocho inteligencias y que en cada individuo y momento se presenta de manera diferente. La relación entre inteligencia y creatividad fue estudiada por Joy Paul Guilford a mediados del siglo XX, estableció un modelo de inteligencia que tenía en cuenta la combinación creativa entre el proceso intelectual, el producto intelectual y el contenido de información. Francis Galton en 1883 llegó a la conclusión de que los productos creativos procedían en su mayoría de la habilidad general. Por todo ello, cabe pensar en que además de las ocho inteligencias hay que tener en cuenta la promoción de la creatividad y su evaluación en cada alumno para que se produzca un desarrollo de la teoría de las inteligencias múltiples óptimo. Página 64 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.3.1. Tipos de inteligencia Hasta la fecha Howard Gardner y su equipo de la Universidad de Harvard han identificado ocho tipos distintos. Inteligencia lingüístico-verbal La función del lenguaje es universal, y su desarrollo en los niños es sorprendentemente similar en todas las culturas. Incluso en el caso de personas sordas a las que no se les ha enseñado explícitamente un lenguaje por señas, a menudo inventan un lenguaje manual propio y lo usan espontáneamente. En consecuencia, podemos decir que, una inteligencia puede operar independientemente de una cierta modalidad en el estímulo o una forma particular de respuesta. Aspectos biológicos - Un área específica del cerebro llamada "área de Broca" (20) es la responsable de la producción de oraciones gramaticales. Una persona con ese área lesionada puede comprender palabras y frases sin problemas, pero tiene dificultades para construir frases más sencillas. Al mismo tiempo, otros procesos mentales pueden quedar completamente ilesos. Capacidades implicadas - Capacidad para comprender el orden y el significado de las palabras en la lectura, la escritura y, también, al hablar y escuchar. Habilidades relacionadas - Hablar y escribir eficazmente. Perfiles profesionales - Líderes políticos o religiosos, oradores, poetas, escritores, etc. Página 65 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia - Debates, escribir diarios, lectura oral, presentaciones, libros, computadoras, grabadoras, etc. Inteligencia lógico-matemática Este tipo de inteligencia se manifiesta mediante la facilidad para el cálculo, para la resolución de problemas, para distinguir la geometría en los espacios, en la satisfacción de crear y solucionar problemas lógicos. Como en el caso de Galileo es la habilidad para distinguir que la naturaleza está escrita en símbolos matemáticos. El científico competente maneja simultáneamente muchas variables y crea numerosas hipótesis que son evaluadas sucesivamente y, posteriormente, son aceptadas o rechazadas. Es importante puntualizar la naturaleza no verbal, pero si como otra forma de comunicación, de la inteligencia matemática. En efecto, es posible construir la solución del problema antes de que ésta sea articulada. Junto con su compañera, la inteligencia lingüística, el razonamiento matemático proporciona la base principal para los test de cociente intelectual. Esta forma de inteligencia ha sido investigada en profundidad por los psicólogos tradicionales, constituyendo, tal vez, el arquetipo de "inteligencia en bruto" o de la validez para resolver problemas que supuestamente pertenecen a cualquier terreno. Sin embargo, aún no se comprende plenamente el mecanismo por el cual se alcanza una solución a un problema lógico-matemático. Página 66 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Las capacidades más implicadas en este tipo de inteligencia son la capacidad para identificar modelos, calcular, formular y verificar hipótesis, utilizar el método científico y los razonamientos inductivo y deductivo. El estímulo de esta inteligencia se inicia muy pronto, cuando el bebé conquista “la permanencia del objeto” (cuando el bebé juega y busca un juguete entre las sábanas). Hacia los seis años, el niño aprende a descifrar y a comparar objetos grandes y pequeños, gruesos y delgados, estrechos y anchos… A partir de esta edad es cuando el niño empieza a experimentar el pensamiento abstracto y la conceptualización simbólica de las relaciones numéricas y geométricas, los sistemas de operación y medida y los conjuntos. Procesos como la clasificación, seriación, relación, composición, inversión, asociación y anulación empiezan a hacerse palpables en el día a día entre los seis y los doce años. Debido a que este proyecto de innovación e investigación educativa está orientado a las matemáticas, en este tipo de inteligencia se pueden diferenciar los siguientes subconjuntos: Capacidad para utilizar los números de manera efectiva. Pensamiento analítico. Pensamiento geométrico. Pensamiento estadístico. Pensamiento intuitivo. Pensamiento lógico-deductivo. Pensamiento crítico. Pensamiento generativo. Pensamiento lateral (Posiblemente para algunos psicólogos, creatividad). Página 67 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Los perfiles profesionales en los que este tipo de inteligencia tiene mayor grado suelen ser economistas, ingenieros, científicos, matemáticos, contadores, etc. Las actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia, están relacionados con la resolución de problemas, cálculos mentales, juego con números, calculadoras, entrevistas cuantitativas, pensamiento crítico, rompecabezas, etc. Inteligencia espacial La resolución de problemas espaciales se aplica a la navegación y al uso de mapas como sistema notacional. Otro tipo de solución a los problemas espaciales, aparece en la visualización de un objeto visto desde un ángulo diferente y en el juego del ajedrez. También se emplea este tipo de inteligencia en las artes visuales. Aspectos biológicos - El hemisferio derecho (en las personas diestras) demuestra ser la sede más importante del cálculo espacial. Las lesiones en la región posterior derecha provocan daños en la habilidad para orientarse en un lugar, para reconocer caras o escenas o para apreciar pequeños detalles. Los pacientes con daño específico en las regiones del hemisferio derecho, intentarán compensar su deficiencia espacial con estrategias lingüísticas, razonarán en voz alta para intentar resolver una tarea o bien se inventarán respuestas. Pero las estrategias lingüísticas no parecen eficientes para resolver tales problemas. Las personas ciegas proporcionan un claro ejemplo de la distinción entre inteligencia espacial y perspectiva visual. Un ciego puede reconocer ciertas formas a través de un método indirecto, pasar la mano a lo largo de un objeto, por ejemplo, construye una noción diferente a la visual de longitud. Para el invidente, el sistema Página 68 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS perceptivo de la modalidad táctil corre en paralelo a la modalidad visual de una persona visualmente normal. Por lo tanto, la inteligencia espacial sería independiente de una modalidad particular de estímulo sensorial. Capacidades implicadas - Capacidad para presentar ideas visualmente, crear imágenes mentales, percibir detalles visuales, dibujar y confeccionar bocetos. Habilidades relacionadas - Realizar creaciones visuales y visualizar con precisión. Perfiles profesionales - Artistas, fotógrafos, arquitectos, diseñadores, publicistas, etc. Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia – Actividades artísticas, mapas mentales, visualizaciones, metáforas, vídeos, gráficos, mapas, juegos de construcción, etc. Inteligencia musical Los datos procedentes de diversas culturas hablan de la universalidad de la noción musical. Incluso, los estudios sobre el desarrollo infantil sugieren que existe habilidad natural y una percepción auditiva (oído y cerebro) innata en la primera infancia hasta que existe la habilidad de interactuar con instrumentos y aprender sus sonidos, su naturaleza y sus capacidades. Aspectos biológicos - Ciertas áreas del cerebro desempeñan papeles importantes en la percepción y la producción musical. Éstas, situadas por lo general en el hemisferio derecho, no están localizadas con claridad como sucede con el lenguaje. Sin embargo, pese a la falta de susceptibilidad concreta respecto a la habilidad musical en caso de lesiones cerebrales, existe evidencia de "amusia" (21) (pérdida de habilidad musical). Página 69 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Capacidades implicadas - Capacidad para escuchar, cantar, tocar instrumentos. Habilidades relacionadas - Crear y analizar música. Perfiles profesionales - Músicos, compositores, críticos musicales, etc. Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia - Cantar, tocar instrumentos, escuchar música, asistir a conciertos, cintas de música, etc. Inteligencia corporal-kinestésica La evolución de los movimientos corporales especializados es de importancia obvia para la especie; en los humanos esta adaptación se extiende al uso de herramientas. El movimiento del cuerpo sigue un desarrollo claramente definido en los niños y no hay duda de su universalidad cultural. La consideración del conocimiento cinético corporal como "apto para la solución de problemas" puede ser menos intuitiva; sin embargo, utilizar el cuerpo para expresar emociones (danza), competir (deportes) o crear (artes plásticas), constituyen evidencias de la dimensión cognitiva del uso corporal. Aspectos biológicos: El control del movimiento corporal se localiza en la corteza motora y cada hemisferio domina o controla los movimientos corporales correspondientes al lado opuesto. En los diestros, el dominio de este movimiento se suele situar en el hemisferio izquierdo. La habilidad para realizar movimientos voluntarios puede resultar dañada, incluso en individuos que puedan ejecutar los mismos movimientos de forma refleja o involuntaria. Página 70 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS La existencia de apraxia específica constituye una línea de evidencia a favor de una inteligencia cinética corporal. Capacidades implicadas: Capacidad para realizar actividades que requieren fuerza, rapidez, flexibilidad, coordinación óculo-manual y equilibrio. Habilidades relacionadas: Utilizar las manos para crear o hacer reparaciones, expresarse a través del cuerpo. Perfiles profesionales: Escultores, cirujanos, actores, modelos, bailarines, deportistas, etc. Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia - Manuales, teatro, danza, relajación, materiales táctiles, deportes, etc. Inteligencia intrapersonal La inteligencia intrapersonal es el conocimiento de los aspectos internos de una persona, el acceso a la propia vida emocional, a la propia gama de sentimientos, la capacidad de efectuar discriminaciones entre ciertas emociones y, finalmente, ponerles un nombre y recurrir a ellas como medio de interpretar y orientar la propia conducta. Las personas que poseen una inteligencia intrapersonal notable poseen modelos viables y eficaces de sí mismos. Pero al ser esta forma de inteligencia la más privada de todas, requiere otras formas expresivas para que pueda ser observada en funcionamiento. La inteligencia interpersonal permite comprender y trabajar con los demás; la intrapersonal, en cambio, permite comprenderse mejor y trabajar con uno mismo. En el Página 71 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS sentido individual de uno mismo, es posible hallar una mezcla de componentes intrapersonales e interpersonales. El sentido de uno mismo es una de las más notables invenciones humanas, simboliza toda la información posible respecto a una persona y qué es. Se trata de una invención que todos los individuos construyen para sí mismos. Aspectos biológicos - Los lóbulos frontales desempeñan un papel central en el cambio de la personalidad, los daños en el área inferior de los lóbulos frontales pueden producir irritabilidad o euforia; en cambio, los daños en la parte superior tienden a producir indiferencia, languidez y apatía (personalidad depresiva). Entre los afásicos que se han recuperado lo suficiente como para describir sus experiencias se han encontrado testimonios consistentes, aunque pueda haber existido una disminución del estado general de alerta y una considerable depresión debido a su estado, el individuo no se siente a sí mismo una persona distinta, reconoce sus propias necesidades, carencias, deseos e intenta atenderlos lo mejor posible. Capacidades implicadas - Capacidad para plantearse metas, evaluar habilidades y desventajas personales y controlar el pensamiento propio. Habilidades relacionadas - Meditar, exhibir, disciplina personal, conservar la compostura y dar lo mejor de sí mismo. Perfiles profesionales - Individuos maduros que tienen un autoconocimiento rico y profundo. Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia – Instrucción individualizada, actividades de autoestima, redacción de diarios, proyectos individuales, meditación, etc. Página 72 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Inteligencia interpersonal La inteligencia interpersonal se constituye a partir de la capacidad nuclear para sentir distinciones entre los demás, en particular, contrastes en sus estados de ánimo, temperamento, motivaciones e intenciones. Esta inteligencia le permite a un adulto hábil, leer las intenciones y los deseos de los demás, aunque se los hayan ocultado. Esta capacidad se da de forma muy sofisticada en los líderes religiosos, políticos, terapeutas y maestros. Esta forma de inteligencia no depende necesariamente del lenguaje. Aspectos biológicos - Todos los indicios proporcionados por la investigación cerebral sugieren que los lóbulos frontales desempeñan un papel importante en el conocimiento interpersonal. Los daños en esta área pueden causar cambios profundos en la personalidad, aunque otras formas de la resolución de problemas puedan quedar inalteradas, una persona no es la misma después de la lesión. La evidencia biológica de la inteligencia interpersonal abarca factores adicionales que, a menudo, se consideran excluyentes de la especie humana: 1. La prolongada infancia de los primates, que establece un vínculo estrecho con la madre, favorece el desarrollo intrapersonal. 2. La importancia de la interacción social entre los humanos que demandan participación y cooperación. La necesidad de cohesión al grupo, de liderazgo, de organización y solidaridad, surge como consecuencia de la necesidad de supervivencia. Capacidades implicadas - Trabajar con gente, ayudar a las personas a identificar y superar problemas. Habilidades relacionadas - Capacidad para reconocer y responder a los sentimientos y personalidades de los otros. Página 73 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Perfiles profesionales - Administradores, docentes, psicólogos, terapeutas y abogados. Actividades y materiales de enseñanza que se podrían emplear para desarrollar esta inteligencia – Aprendizaje cooperativo, tutorías, juegos de mesa, materiales para teatro, etc. Inteligencia naturalista Se describe como la competencia para percibir las relaciones que existen entre varias especies o grupos de objetos y personas, así como reconocer y establecer si existen distinciones y semejanzas entre ellos. Los naturalistas suelen ser hábiles para observar, identificar y clasificar a los miembros de un grupo o especie, e incluso, para descubrir nuevas especies. Su campo de observación más afín es el mundo natural, donde pueden reconocer flora, fauna y utilizar productivamente sus habilidades en actividades de caza, ciencias biológicas y conservación de la naturaleza. Pero puede ser aplicada también en cualquier ámbito de la ciencia y la cultura, porque las características de este tipo de inteligencia se ciñen a las cualidades esperadas en personas que se dedican a la investigación y siguen los pasos propios del método científico. En realidad, todos aplicamos la inteligencia naturalista al reconocer plantas, animales, personas o elementos de nuestro entorno natural. Las interacciones con el medio físico nos ayudan a desarrollar la percepción de las causas y sus efectos y los comportamientos o fenómenos que puedan existir en el futuro; como por ejemplo la Página 74 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS observación de los cambios climáticos que se producen en el transcurso de las estaciones del año y su influencia entre los humanos, los animales y las plantas. Gardner postula que este tipo de inteligencia debió tener su origen en las necesidades de los primeros seres humanos, ya que su supervivencia dependía, en gran parte, del reconocimiento que hicieran de especies útiles y perjudiciales, de la observación del clima y sus cambios y de ampliar los recursos disponibles para la alimentación. Inteligencia creativa La inteligencia creativa ha sido definida por diversos autores a lo largo de la historia. Por ejemplo para Guilford, la creatividad es la capacidad para generar información nueva a partir de la existente o previa, para Torrance, la creatividad es un proceso por el cual una persona, es sensible a los problemas, a los fallos, a las lagunas de conocimiento y a las desarmonías en general. Una persona creativa se caracteriza por disponer de una gran predisposición a la experiencia, carencia de prejuicios e inhibiciones, sensibilidad estética, flexibilidad cognitiva, independencia de pensamiento y de acción, alto nivel de energía creativa, dedicación al esfuerzo creativo y búsqueda constante de soluciones a los problemas difíciles que se plantean, en el que se dan a la vez una serie de características cognitivas, de personalidad y motivación y de experiencias. Hay estudios que definen al niño creativo, al estudiante de primaria creativo y al adolescente creativo. Me centraré en las características del adolescente. Suelen ser talentosos, con altos rendimientos, líderes de grupos sociales, con un gran desarrollo intelectual y en ciertas ocasiones rebeldes. Página 75 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.3.2. Combinación de factores Según esta teoría, todos los seres humanos poseen las ocho inteligencias en mayor o menor medida. Al igual que con los estilos de aprendizaje, no hay estilos puros, y, si los hubiera, les resultaría imposible funcionar. Un ingeniero necesita una inteligencia espacial bien desarrollada, pero también necesita de todas las demás, de la inteligencia lógico matemática para poder realizar cálculos de estructuras; de la inteligencia interpersonal para poder presentar sus proyectos; de la inteligencia corporal - kinestésica para poder conducir su coche hasta la obra, etc. Gardner enfatiza el hecho de que todas las inteligencias son igualmente importantes y, según esto, el problema sería que el sistema escolar vigente no las trata por igual, sino que prioriza las dos primeras de la lista, (la inteligencia lógico -matemática y la inteligencia lingüística). Sin embargo, en la mayoría de los sistemas escolares actuales se promueve que los docentes realicen el proceso de enseñanza y aprendizaje a través de actividades que promuevan una diversidad de inteligencias, asumiendo que los alumnos poseen diferente nivel de desarrollo de ellas y, por lo tanto, es necesario que todos las pongan en práctica, pero ni los profesores están preparados para afrontar este reto, ni el sistema educativo con los currículos tal y como están redactados permiten llevar a cabo estas prácticas. Para Gardner es evidente que, sabiendo lo que se sabe sobre estilos de aprendizaje, tipos de inteligencia y estilos de enseñanza, es absurdo que se siga insistiendo en que todos los alumnos aprendan de la misma manera. La misma materia se podría presentar de formas muy diversas, permitiendo al alumno asimilarla partiendo de sus capacidades y aprovechando sus puntos fuertes. Además, tendría que plantearse si una educación centrada básicamente en ciertos subconjuntos de dos tipos de Página 76 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS inteligencia es la más adecuada para preparar a los alumnos para vivir en un mundo cada vez más complejo. Por otro lado, y como contraposición a esta teoría cabría suponer que si no somos capaces de combinar las diferentes inteligencias propuestas por Gardner no alcanzaríamos nuestro grado de inteligencia óptimo, pero la teoría de Gardner puntualiza que no hay que saber combinar todas sino combinar solo las que produzcan en cada alumno un grado de inteligencia óptimo. Por último, cabe destacar que si la búsqueda de las mejores combinaciones de inteligencias en cada alumno es la forma más óptima de producir el aprendizaje en cada alumno, supone además conocer qué procesos y estados mentales y qué conexiones existen y se desean desarrollar en el cerebro de los adolescentes, aspecto éste último enmarcado en la neuropsicología. 4.3.3. Uso en la educación Gardner define a la inteligencia como “la capacidad de resolver problemas y/o elaborar productos que sean valiosos en una o más culturas”. De acuerdo con Gardner, hay muchas maneras de hacer esto y no sólo por medio de la inteligencia matemática y lingüística. Gardner cree que el propósito de la escuela “debería de ser desarrollar todas las inteligencias y ayudar a las personas a alcanzar metas que sean apropiadas para su inteligencia (la cual tengan más desarrollada). Las personas que son ayudadas para hacer esto, él cree que van a ser más comprometidas y competentes, por lo tanto, más inclinadas a servir a la sociedad de una manera constructiva. Gardner sostiene que el test de cociente intelectual, se enfoca mayormente en la inteligencia lógico matemática y la inteligencia lingüística. Y al sacar buena calificación Página 77 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS en estas pruebas, la posibilidad de asistir a un colegio o universidad de prestigio es mayor que los que sacaron un porcentaje bajo. Mientras muchos estudiantes trabajan bien bajo este ambiente, también hay otros que no. De acuerdo con Helding (2009), “El estándar del test del cociente intelectual mesura el conocimiento adquirido en un momento en particular, estos test sólo pueden proporcionar una visión “congelada” del conocimiento. Pero no pueden evaluar o predecir la capacidad de una persona para aprender, para asimilar la nueva información, o para resolver nuevos problemas”. La teoría de Gardner argumenta que los estudiantes tendrán una mejor educación si se tiene una visión más amplia de ésta, en donde los profesores usen diferentes metodologías, ejercicios y actividades que lleguen a todos los estudiantes, no sólo a aquellos que tienen éxito en la inteligencia lingüística y matemática, sino a todos los alumnos. Esta teoría desafía a los docentes a encontrar formas que funcionen para los diferentes estudiantes a aprender el tema que se imparte, como podría ser por medio de actividades o experiencias (obras de teatro, crear programas de radio o televisión, hacer carteles, tomar fotografías, diseñar, crear coreografías, escribir poemas, pintar entre otros métodos), el trabajo por proyectos, tan de actualidad en nuestros actualmente o la creación de árboles con caminos o trayectorias de aprendizaje (19). Por otro lado, cabe destacar que la teoría de Gardner no ha sido aceptada por muchos académicos o profesores en inteligencia. Gardner postula que “mientras la Teoría de las Inteligencias Múltiples aunque consistente con mucha evidencia empírica, no ha sido sometida a pruebas experimentales fuertes… sin embargo en el área de educación, actualmente se está examinando en muchos proyectos la aplicación de esta teoría en el proceso de enseñanza-aprendizaje, como es el proyecto “Spectrum”, o como puede ser el ejemplo del Colegio Montserrat en Barcelona. Página 78 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS George Miller, un psicólogo cognitivo muy distinguido, escribió en el periódico “The New York Times Book Review” que los argumentos de Gardner consisten en “corazonadas y opiniones”. Jerome Bruner llamó a las “inteligencias” de Gardner como “la ficción más útil”, y Charles Murray y Richard J. Herrnstein en The Bell Curve, mencionan que la teoría de Gardner “esta carente de evidencia psicométrica u otra evidencia cuantitativa”. Thomas Armstrong argumenta que la educación de Waldorf emplea las 7 inteligencias originales de Gardner. A pesar de la falta de aceptación en la comunidad de la psicología, la teoría de Gardner ha sido aceptada y adoptada por muchas escuelas, en donde por lo general es utilizada para sustentar el debate sobre los estilos y métodos de aprendizaje. El mismo Gardner ha dicho que "le inquieta" la forma en que su teoría ha sido usada en la educación. Por ello, es necesario entrar todavía más en profundidad sobre la aplicación de la teoría de Gardner, para poder ver exactamente qué puede aportar por ejemplo en las clases de matemáticas de un centro de educación secundaria. 4.4. DESCRIPCIÓN DEL PROYECTO VS INNOVACIÓN El proyecto de innovación docente sobre el que versa este trabajo se centra en la utilización de la teoría de las inteligencias múltiples dentro de una clase de matemáticas a través de diversas actividades interdisciplinares y con la utilización de diferentes recursos. A priori la aplicación de esta teoría de las inteligencias múltiples, puede verse como el mero hecho de dar una formación (siempre atendiendo a las competencias del Página 79 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS currículo correspondiente) mediante actividades enmarcadas en varias asignaturas a la vez, en lugar de la forma tradicional con un libro de texto por asignatura con contenidos específicos de la misma. Pero fuera convencionalidades, esta teoría puede ir más lejos, ya que el simple hecho de plantear la formación a través de actividades interdisciplinares, obliga la coexistencia en el mismo aula de varios profesores, lo que incide en una mejor atención a la diversidad y por lo tanto la educación es más personalizada a los requerimientos y necesidades educativas, de desarrollo psicoevolutivo y de aprendizaje que cada alumno tiene. Desde un punto de visto más arcaico, se puede ver este planteamiento como una excusa nueva para poner más profesores en los centros, pero no nos podemos quedar con un planteamiento tan simplista ya que si los alumnos integran varios contenidos y aprendizajes a la vez, se produce un proceso educativo más significativo y el desarrollo de los alumnos es mucho más integro, ya que son capaces de buscar y entender relaciones y conectar más fácilmente con sus pensamientos. Además, otro aspecto importante a destacar, es que si bien todos los alumnos deben alcanzar unos “mínimos” establecidos en el currículo correspondiente, no es necesario que todo el contenido teórico sea visto y aprendido por los alumnos. En el currículo de ESO de La Rioja, se dicen las siguientes frases, a analizar respecto de la educación actual y a lo que la aplicación de la teoría de las inteligencias múltiples puede ayudar: 1. “Los contenidos básicos de las enseñanzas mínimas requerirán el 65 % de los horarios escolares”. De esta frase cabe pensar que existe el tiempo suficiente para la realización de actividades adaptadas a las necesidades de los alumnos, que abarquen bien todas sus capacidades sin desaprovechar las potencialidades de cada uno, por ejemplo, mediante la aplicación de la teoría de las inteligencias múltiples. Página 80 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2. “El presente decreto define las competencias básicas que el alumnado debe alcanzar al finalizar la etapa de Educación Secundaria Obligatoria, así como los objetivos, contenidos y criterios de evaluación correspondientes a cada una de las materias que la integran. Para ello, se ha tenido en cuenta, en primer lugar, el doble carácter de la etapa, orientada, por una parte, a proporcionar el bagaje necesario para la incorporación al mundo laboral; y, por otra, a preparar con garantías de aprovechamiento y superación a aquellos alumnos que vayan a continuar estudios, lo que exige una combinación de rigor científico y flexibilidad suficiente para hacer frente a ambos retos. Y, en segundo, la evolución y los grandes cambios que se producen a estas edades, que aumentan la complejidad intrínseca de la etapa y obligan a conciliar la formación común con la necesidad de ofrecer variedad de opciones a unos jóvenes a los que hay que iniciar en la libertad de elección, y en la responsabilidad y compromiso con las decisiones tomadas como objetivos esenciales de todo proceso educativo.” Estas dos partes bien diferenciadas, la de dar un bagaje de conocimientos y una amplitud para aquellos que quieran seguir sus estudios por un lado y por otro la atención a la diversidad y a los cambios sociales, es donde los profesores encuentran en su día a día todas sus dificultades, por ello la aplicación de la teoría de las inteligencias múltiples puede ayudar a poner en sincronía ambos objetivos. 3. “La Educación Secundaria Obligatoria debe suponer una progresión con respecto a la etapa anterior, completar los territorios conceptuales delimitados en la Educación Primaria, y advertir, a través de la reflexión sobre las informaciones recibidas, las líneas maestras, vertebradoras, de cada materia” Cabe plantearse si, la posibilidad de apertura y progresión que ofrece el salto Página 81 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS de primaria a secundaria en los alumnos a la hora de conocer nuevos alumnos y cambiar de entorno escolar, realmente conviene ya que la diversidad de aprendizajes y procedencias de los alumnos es tal que no permite poner en común criterios de modelos de aprendizaje adecuados en cada caso desde un planteamiento tradicional del modelo de educación secundaria. Actualmente este planteamiento cuando no existen los recursos adecuados redunda en malos resultados escolares, por lo tanto porque no hacer una educación que realmente atienda a la diversidad y que además se estructure como un proceso íntegro y completo donde los profesores tanto de primaria como secundaria compongan un ámbito educativo de colaboración y correcta relación donde la comunicación en ambas direcciones sea todo lo transparente que debe ser, dejando de un lado los intereses de centro de cada momento, para que en los alumnos se produzca una correcta construcción de la sociedad del entorno de los centros. A la colaboración entre profesores de primaria y secundaria en las aulas puede contribuir la aplicación de la teoría de las inteligencias múltiples. 4. “Una formación teórica lo más exigente posible que puedan ir incrementando a lo largo de la vida, guiada por la curiosidad intelectual como estímulo para el aprendizaje permanente. Sólo habiendo accedido a buenas introducciones a las diferentes disciplinas, sólo desde unos cimientos sólidos y rigurosos puede construirse una actitud inteligente y crítica ante los retos del futuro.” Si bien es cierto que hay que tener unos conocimientos teóricos de ciertas cosas, no por ello tenemos que menoscabar la creatividad de nuestros alumnos, hay un 35%, como se señalaba anteriormente, de las clases y contenidos que no tienen por qué ser los de siempre y a ello puede contribuir la aplicación de la teoría de las inteligencias múltiples. Por otro lado también hay que destacar de que la Página 82 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS docencia de parte de los conocimientos base se podrían ofrecer en los últimos cursos de primaria (además como señal de progreso intelectual de nuestra sociedad), ya que el desarrollo mental de los niños cada vez es más precoz y rápido. 5. “Debe garantizarse que los alumnos dominen no sólo las destrezas fundamentales del cálculo matemático, los fundamentos del desarrollo tecnológico o las lenguas, sino que hayan obtenido un conocimiento suficiente sobre qué son las Ciencias, las Matemáticas, la Música, la Literatura, la Historia, la Geografía”. Éste es un planteamiento que divide los conocimientos por asignaturas cerradas y no por inteligencias a desarrollar, a lo cual puede contribuir la aplicación de la teoría de las inteligencias múltiples. 6. “Las enseñanzas comunes iniciales desemboquen, conforme se avanza en la etapa, en una trayectoria personalizada y libremente asumida.”. En la actualidad, la realidad choca con este texto ya que la educación no atiende a la diversidad adecuadamente, por mucho que existan programas de diversificación, atención a alumnos extranjeros (hay que analizarlos caso por caso) y por lo tanto los alumnos no adquieren la capacidad adecuada para descubrir sus propias capacidades y crear una trayectoria personalizada libremente asumida, a lo cual puede ayudar la aplicación de la teoría de las inteligencias múltiples. 7. “El reconocimiento de la figura del profesor como encarnación de la sabiduría que es consecuencia de haber devuelto el protagonismo escolar a la cultura”. Este planteamiento esta desactualizado y no responde en muchos casos a la realidad, es necesario saber en qué casos el docente debe ser el transmisor de conocimientos, valores, costumbres y modelos y en cuales el Página 83 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS docente debe hacer de promotor del desarrollo de potenciales mentales y guía que ayude al alumno a avanzar en su progreso intelectual aunque no disponga de los conocimientos adecuados. Este análisis de ciertos puntos del currículo de enseñanza de secundaria de La Rioja, sirve como punto de partida para ver donde puede ayudar el desarrollo de la teoría de las inteligencias múltiples en las aulas de secundaria. Este proyecto trata de realizar un compendio de actividades fácilmente implementables en el devenir de un aula de matemáticas. Dividiendo las actividades por las inteligencias contempladas en la teoría de Gardner e incorporándolas a las unidades didácticas de cada asignatura tradicional de manera colaborativa por parejas de profesores, es decir, integrando unidades didácticas de varias asignaturas tradicionales, de modo que se pueda dar un proceso de adaptación desde las actuales asignaturas, a las futuras clases de inteligencias o habilidades. No se trata de un cambio de 180º del paradigma educativo, sino de un camino o un medio de adaptación de la enseñanza a las nuevas necesidades de los alumnos y de la sociedad, además de otro modo y punto de vista diferente de la enseñanza que puede ser útil en según qué situaciones. Y en el cual es necesario asumir que es un modelo de proceso de enseñanza-aprendizaje en el que no es posible capacitar a un docente para afrontar la diversidad de perfiles intelectuales de los alumnos, pero si concienciarle de que es esencial que aprenda constantemente nuevas teorías, técnicas y metodologías a fin de desempeñarse en un medio que demanda un continuo avance del saber educativo. Todas las actividades se desarrollan con el uso del mayor abanico posible de recursos disponible o conocido desde el docente, sea material on-line, pizarra digital, tablets, cuadernos tradicionales, juegos, nuevas disciplinas (ajedrez),…., etc. Partiendo Página 84 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS además de un planteamiento diferente al comúnmente socializado sobre el uso y aprendizaje de las tecnologías por parte de los alumnos, y es que tenemos que entender que nuestros alumnos de hoy y mañana son nativos digitales y por tanto no necesitan ser enseñados en la utilización de las mismas sino en la correcta utilización de las mismas para producir en ellos mismos el mejor aprendizaje. Esto supone saltarnos el planteamiento de que no todos tienen acceso a los medios informáticos, pero según el estudio realizado en Mayo de 2011 por el Instituto de Tecnologías Educativas sobre los indicadores y datos de las tecnologías de la información y comunicación en la educación en Europa y España (22), refleja que en 2009 que el 60% de los alumnos españoles tienen acceso a Internet, el 99,7% de centros educativos tenía acceso a Internet, el número de alumnos por ordenador destinado a tareas de aprendizaje era de 5,3, en 2010 cerca del 70% de los hogares españoles disponían de PCs y que entorno al 75% de los niños con edades comprendidas entre 10 y 15 años disponían de teléfono móvil, lo que supone un acceso a la servicios informáticos casi por parte de todo el alumnado en España, por lo que la consideración de que todos son nativos digitales está justificada. El planteamiento de este proyecto de innovación educativo está enmarcado en las clases de educación secundaria, ya que como algunos estudios dicen, en esta etapa el desarrollo psico-evolutivo del alumno depende en gran manera de factores sociales, culturales y curriculares, por lo que en esta etapa la educación debe ser todavía más personalizada que en primaria. Página 85 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.5. METODOLOGÍA El modo en que se llevan a cabo las actividades o experiencias para que se produzca un aprendizaje significativo en base al modelo de enseñanza-aprendizaje de inteligencias múltiples, desde mi punto de vista, debe reconocer que las diversas inteligencias coexisten combinadas unas con otras y además están incorporadas en diferentes asignaturas tradicionales. Sin embargo, las inteligencias múltiples no se desarrollan en una hora o de manera secuencial, es decir, a una hora se trabaja una inteligencia y a otra la siguiente. Al alumno se le debe enfrentar a un conjunto de procesos en una misma experiencia, si durante el proceso de aprendizaje alguna de las inteligencias no está lo suficientemente desarrollada el evento se debilita impidiendo obtener el objetivo buscado. El trabajo por proyectos y la organización del grupo es la manera en que se pueden trabajar las inteligencias múltiples. Haciendo asumir determinados papeles diferentes en cada proyecto a todos los componentes del grupo y utilizando el profesor los que considera más oportunos para cada alumno en cada actividad o experiencia. Trabajar en grupos pequeños permite una organización física diferente, todos son parte de un grupo pero trabajan de manera independiente, comparten el mismo espacio, algunos materiales, pero no las formas de pensamiento plasmadas en las ideas. Estos grupos no deben organizarse por habilidades intelectuales para permitir la interacción heterogénea y enriquecer el quehacer académico. El trabajo en grupos colaborativos permite la participación en la construcción de una tarea o conocimiento, se combinan y aprovechan las diversas habilidades al mismo tiempo que se comparten las responsabilidades. Cuando se trabaja en grupos cooperativos cada alumno puede tener una función diferente y todas las funciones son necesarias para el cumplimiento de la Página 86 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS tarea, es decir, de manera complementaria. La combinación en cada caso de estos tres planteamientos para organizar al grupo ofrece una amplia gama de posibilidades en el desarrollo del perfil intelectual de los alumnos. La estrategia a seguir para implementar esta metodología en un aula de secundaria debe partir de situaciones reales y análisis de acontecimientos y objetos o fenómenos a observar, seguir por ver que conceptos están involucrados en los mismos y los procedimientos y leyes que se pueden utilizar, para a continuación realizar una serie de preguntas de investigación sobre los datos, y por ultimo las conclusiones, opiniones y afirmaciones de las resoluciones planteadas. Mediante el planteamiento de las inteligencias múltiples en un aula de matemáticas, el docente puede mostrar al grupo la utilización de técnicas como la visualización, dibujos, gráficas y discutir con otros estudiantes para analizar el problema y encontrar soluciones, de modo que se abra el camino para ir interrelacionando las diferentes subcategorías de inteligencias matemáticas, en colaboración con otras áreas de conocimiento haciendo de estas actividades, formas de trabajo interdisciplinar. La expresión oral y escrita también propicia en los alumnos el uso del pensamiento lógico y la imaginación. La ejecución de piezas musicales y el movimiento en algunas artes plásticas y visuales resultan actividades perfectas para la estimulación de las inteligencias corporal, espacial y musical. Para ello el docente debe estar familiarizado con las diferentes técnicas y métodos empleados de enseñanza en cada asignatura tradicional para estimular la mente de los alumnos de la manera que se requiera en cada momento y de forma innovadora. Otro aspecto a destacar en el empleo de este planteamiento es que el docente debe estar muy al tanto de la información que se proporciona a cada alumno de modo Página 87 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS que le permita indagar, buscar y encontrar información viviendo la experiencia en sí mismo y así se fomente un dialogo constructivo entre toda la clase. A continuación se ofrecen ejemplos de técnicas, estrategias, actividades y experiencias para el desarrollo de cada inteligencia. 1. Para el desarrollo de la inteligencia lingüística: Actividades en las que los alumnos lean, escuchen, hablen o escriban. Contar historias, leer libros a los escolares y dejar que ellos lean, escribir diarios, generar lluvias de ideas, escribir textos, boletines o periódicos, dramatizar las lecturas, hacer un censo en la escuela, hacer entrevistas, establecer debates, realizar actividades en las cuales simulen o representen, escribir canciones, participar en obras de teatro, hacer diarios. 2. Para el desarrollo de la inteligencia lógico-matemática como tal: Actividades en las que los escolares trabajen con números o necesiten pensar lógicamente, deducir o relacionar causas y efectos: clasificar datos recolectados en investigaciones hechas en la clase, crear nuevas categorías para un conjunto de objetos aparentemente no relacionados, hacer cálculos matemáticos utilizando ejemplos relevantes de la vida diaria, analizar gráficas de información de algún tema, resolver acertijos o juegos utilizando el pensamiento lógico, utilizar la computadora, hacer debates sobre un tema, armar rompecabezas, contar historias. 3. Para el desarrollo de la inteligencia musical: Actividades en las que los estudiantes escuchen música, canten, utilicen ritmos o diferentes tonos: Poner música cuando están trabajando, utilizar varios tonos de voz y sonidos cuando leen en voz alta, deletrear palabras o recitar listas de información siguiendo el ritmo de una canción popular, organizar un recital, componer música sencilla Página 88 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS escoger una canción que represente las emociones que provoca un poema o una narración, contar historias, crear una coreografía, hacer una obra de teatro, escribir canciones. 4. Para el desarrollo de la inteligencia espacial: Actividades relacionadas con colores, artes plásticas que faciliten el proceso de visualización: imaginar escenas de una narración, ilustrar composiciones escritas, clasificar por colores los elementos importantes de una lectura (subrayar con un color la idea principal y con otro las secundarias), diseñar proyectos de arte con materiales reciclables, contar historias, armar rompecabezas, pintar, participar en una obra de teatro. 5. Para el desarrollo de la inteligencia kinestésico-corporal: Actividades donde los escolares se muevan, construyan, toquen: participar en una obra de teatro con el tema de la unidad, dramatizar situaciones cotidianas y relevantes, teatro guiñol, manipular objetos para la enseñanza de conceptos matemáticos, hacer representaciones de bailes, simular y representar hechos históricos, contar historias, crear una coreografía, hacer deportes, hacer excursiones, pintar. 6. Para el desarrollo de la inteligencia interpersonal: Actividades que requieren l participación de más de un alumno: trabajo en equipo, realizar proyectos en grupo, compartir el trabajo individual con una pareja para discutir las ideas, conclusiones o dudas, participar en deportes de conjunto o en juegos colaborativos, hacer un censo en la escuela, hacer entrevistas, participar en debates, contar historias, armar rompecabezas, simular o representar, pintar, participar en obras de teatro, hacer diarios. 7. Para el desarrollo de la inteligencia intrapersonal: Requiere que el docente evalúe las experiencias previas de los estudiantes y establezca relaciones entre ellas y el tema que se va a trabajar, es importante dar tiempo para reflexionar y Página 89 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS analizar las propias emociones de los escolares: interrumpir las sesiones de clase para dedicar un minuto para pensar sobre un sentimiento en silencio, discutir sobre temas polémicos para evocar emociones, dedicar tiempo en las sesiones de clase para establecer metas para guiar el aprendizaje, permitir a los alumnos seleccionar proyectos o actividades que les interesen, hacer investigaciones individuales sobre algún tema, usar la computadora, relatar historias, armar rompecabezas, crear una coreografía, escribir canciones, poemas o diarios. 8. Para el desarrollo de inteligencia naturalista: Actividades que incorporan la naturaleza, trabajar fuera del salón de clases: cultivar huertos, aprovechar lo que la naturaleza ofrece e incorporarlo en el proceso de enseñanza-aprendizaje, clasificar plantas, hojas, flores, animales, comparar características de diferentes especies de animales, observar a través del microscopio o telescopio, narrar historias, hacer excursiones. 9. Para el desarrollo de la inteligencia creativa: El profesor fomentará la comunicación, el intercambio de ideas y la ayuda entre alumnos. Debe crear el clima adecuado en la clase un ambiente relajado y sin tensiones para surjan pensamientos nuevos. Debe desarrollar en los alumnos la originalidad, la fluidez, la flexibilidad, la elaboración el ingenio y actitudes como la curiosidad, la tolerancia a la ambigüedad, la independencia, la sensibilidad, las imágenes mentales, el pensamiento metafórico, el pensamiento lógico, encontrar el orden en el caos, preguntarse el porqué de las cosas. Facilitando recursos que favorezcan la creatividad como son cuentos, mitos, fabulas, dar tiempo para que el alumno piense y sueñe despierto sin actividades agobiantes conformistas. Animar a que expresen sus ideas. Aceptar la tendencia a adoptar diferentes puntos de vista. Página 90 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS El planteamiento principal de esta metodología es convertir el aula en un pequeño laboratorio de aprendices donde realizar experimentos de diferentes tipologías y de los que aprender entre todos. El procedimiento para diseñar una instrucción individualizada se desarrolla en cuatro fases: 1. La primera fase, consiste en introducir y mostrar a los niños un amplio rango de áreas de aprendizaje. 2. La segunda fase, se centra en identificar los puntos fuertes de las ocho áreas o inteligencias y a través de estos paliar los desfases o lagunas. 3. La tercera fase, se orienta a fomentar los puntos fuertes que se han identificado. 4. La cuarta fase, trata de construir y enseñar a transferir los puntos fuertes de los alumnos a otras áreas. A continuación una serie de propuestas educativas y de experiencias para el desarrollo del método de enseñanza-aprendizaje basado en la teoría de las inteligencias múltiples. 4.5.1. Actividades de tipo Juegos (Ver Anexo 5) 4.5.2. Actividades tipo laboratorio virtual o presencial (Ver Anexo 6) 4.5.3. Actividades de fomento de la creatividad matemática (Ver Anexo 7) Página 91 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.5.4. Conclusiones sobre la metodología empleada Con la utilización de esta metodología, al integrar diversos conocimientos y poder trabajar por proyectos las diferentes competencias o inteligencias estipuladas en el currículo correspondiente, se le da más espacio al alumno para que pueda desarrollar sus propios descubrimientos del día a día sin por ello menoscabar la capacidad de esfuerzo y el contenido conceptual básico de los antiguos currículos y además enseñando al alumno a aprender a aprender. Sería bueno tener un base de árboles de aprendizaje modificable con actividades enlazadas en función de cada camino de aprendizaje para cada tipología que ayudase al docente en todo momento saber interpretar el tipo de clase que tiene y como puede afrontarla de la mejor manera. 4.6. EVALUACIÓN Uno de los elementos más importantes en la intervención pedagógica es la evaluación, la cual debe ser congruente con la propuesta educativa. El hablar de inteligencias múltiples implica eliminar la evaluación que reconoce únicamente las habilidades lingüísticas o lógico-matemáticas de los adolescentes, requiere de una evaluación acorde con los conceptos teóricos que la fundamentan. Esta teoría requiere de un proceso real de evaluación a través del cual se pueda observar una continuidad de habilidades puestas en acción simultáneamente, ya que ninguna inteligencia se manifiesta aisladamente y se debe tener en cuenta que si bien todos los alumnos no son de igual manera hábiles en las diferentes inteligencias, en cada alumno el proceso de maduración y desarrollo no es igual a mismas edades, pero el docente se debe asegurar Página 92 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS de que al finalizar los estudios “obligatorios” cada alumno haya tenido la posibilidad de alcanzar su mayor grado en todas las inteligencias. Una evaluación autentica de este planteamiento de las inteligencias múltiples demanda que los estudiantes se involucren en un proceso continuo de reflexión y revisión de su propio aprendizaje, mediante además una evaluación tanto conceptual como procedimental. La evaluación deberá ser continua y deberá tener en cuenta aspectos como crear, entrevistar, demostrar, solucionar problemas, reflexionar, dibujar, discutir y participar activamente en diferentes actividades de aprendizaje, es decir, la evaluación se encuentra en las situaciones de aprendizaje y es de forma dinámica. Para ello, es conveniente elaborar un portafolio donde el docente y los alumnos incorporen muestras significativas del trabajo realizado durante el ciclo escolar. Es necesario hacer un seguimiento continuo del progreso de los estudiantes no solo en el aspecto cognitivo, sino también en el desarrollo de las habilidades de sus potencialidades intelectuales, para valorar el impacto de las estrategias de enseñanza y su grado de eficacia en el proceso de enseñanza-aprendizaje. Como primer acercamiento a la evaluación dinámica se plantea el modelo propuesto por Vigotsky cuando define la zona de desarrollo potencial (ZDP) y la capacidad que tiene el niño o adolescente para aprender más allá de su desarrollo real. El segundo planteamiento se centra en el estudio del modelo de Feuerstein, inspirado en la teoría de la interacción social de Vigotsky, consistente en valorar el potencial cognitivo mediante sesiones tipo pretest-entrenamiento-postest. En definitiva, realizar una serie de propuestas de evaluación para el modelo de enseñanza basado en la teoría de las inteligencias múltiples, que favorezcan la correcta percepción por parte del Página 93 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS entorno educativo del desarrollo intelectual de los alumnos y favorecer el potencial oculto que puede conllevar cualquier situación para ellos mismos, de manera que exista una retroalimentación continua. El modelo de Feuerstein: El objetivo de este modelo de evaluación no es medir el cociente intelectual o capacidades del individuo en un momento determinado, sino sus posibilidades de cambio estructural cognitivo hacia el futuro y la capacidad de aprovechar la instrucción recibida para modificar en consecuencia su funcionamiento cognitivo, partiendo de un planteamiento teórico que concibe al ser humano como un organismo abierto al cambio y con una inteligencia dinámica, flexible y receptora a la intervención positiva de otro ser humano. Otro de los exponentes educativos de los que se pueden recoger aportaciones en el campo de la evaluación es, Buddof, cuyo planteamiento pretende mejorar la actuación de las pruebas convencionales sobre una población específica de niños con cociente intelectual bajo con unas pruebas de potencial de aprendizaje que presentan una serie de características: 1. El procedimiento esta explícitamente diseñado para ofrecer una alternativa a las pruebas de inteligencia convencionales empleadas para seleccionar y clasificar a los niños que deban recibir educación especial. 2. Solo se emplean prueban normalizadas, fiables y validadas de una manera exhaustiva. 3. El objetivo de la enseñanza o instrucción es familiarizar a los estudiantes con las exigencias de las pruebas, intentando de esta manera equiparar sus experiencias. Página 94 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Además Buddof categoriza los alumnos en función de una clasificación cuantitativa de casos, por: 1. Niños que obtienen índices altos de potencial para aprender. 2. Los que manifiestan un gran potencial para beneficiarse de los aprendizajes. 3. Los que manifiestan incapacidad para aprender. Las medidas de Buddof son instrumentos sólidos para su objetivo concreto y limitado, sin embargo, se puede comprobar que se pueden encontrar niños que obtienen buenos resultados en pruebas cognitivas, pero tienen un ritmo lento de aprendizaje, viceversa, tanto en poblaciones con niños de alto cociente intelectual como en poblaciones con niños más desfavorecidos. Por ello, es bueno plantear un conjunto de puntuaciones distribuidas cuantitativamente a la vez que unas normas específicas de evaluación que permitan comparar las puntuaciones obtenidas con las puntuaciones normativas. Otros como Campione y Brown, proponen un modelo de “sugerencias graduadas”, cuya operacionalización reside en la cuantificación de indicadores del aprendizaje y de la transferencia. Esta cuantificación se realiza sobre un paradigma de aprendizaje guiado. La secuencia típica de la prueba consta de varias sesiones que incluyen: 1. Recogida de información estática relativa al nivel de actuación (pretest). 2. El aprendizaje inicial (fase de sugerencia). 3. Comprobación del mantenimiento estático y no mediado y de la transferencia (postest). 4. Comprobación del mantenimiento mediado y de la transferencia (postest asistido con sugerencias). Página 95 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Y considera que el procedimiento de instrucción tiene éxito si la actuación en la tarea mejora como consecuencia de la instrucción, el efecto de la instrucción es duradero y el resultado de la instrucción se puede generalizar, es decir, si se produce una transferencia a tareas distintas de aquellas en las que ha tenido lugar la instrucción. La medida resultante se interpreta como el número mínimo de sugerencias necesarias para que cada individuo alcance una cantidad dada de aprendizaje, en lugar de centrarse en la cantidad de mejora de la actuación de un estudiante. Esta postura difiere de la adoptada por la mayoría de los examinadores dinámicos (Budoff, Guthke) que destacan el máximo grado de mejora en la actuación, es decir, la medida en que el individuo rinde mejor en el postest que en el pretest. Después de estos análisis sobre métodos de evaluación dinámica, podemos establecer algunas diferencias entre la evaluación estática y la dinámica. La primera, es que las pruebas estáticas destacan los productos resultantes de las aptitudes preexistentes, mientras que las pruebas dinámicas destacan la cuantificación de los procesos psicológicos que intervienen en el aprendizaje y en el cambio. La segunda es que en las pruebas estáticas el examinador presenta una sucesión de problemas de dificultad creciente y el sujeto debe responder a cada problema, sin ofrecer retroalimentación, y en las dinámicas, esta retroalimentación se da de manera explícita o implícita. La tercera, es que en las estáticas el examinador procura no intervenir y ser lo más neutral posible, suponiendo que ir más allá en la comunicación con el alumno supone un riesgo de introducir errores en la medida, mientras que en las dinámicas, la situación de prueba y la relación entre alumno y examinador tiene un enfoque bidireccional e interactivo. A modo de resumen la tabla siguiente muestra las características de los planteamientos vistos hasta ahora sobre evaluaciones dinámicas. Página 96 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS PODER DE ENFOQUE MÉTODO POBLACIÓN FORMATO CONTEXTO OBJETIVO ORIENTACIÓN PREDICCIÓN Teoría de la modificabilidad de LPAD (Learning la estructura Potential Assesment cognitiva Device) (Feuerstein y otros) Pruebas del potencial de aprendizaje (Budoff y otros) Todos los individuos que pueden hacer uso de Test-mediación-test. Preparación experimentado Pretest formal- centrada en la fracaso escolar instrucción/preparación-postest prueba. (estudiantes con formal graduadas) contexto del programa escolar); problemas de razonamiento estructurales Centrado en el niño. cognitivos. No está bien establecido. Mejora del rendimiento de Centrado en la tarea Muy alto Centrado en la tarea. No está establecido. la prueba abstracto. Con la excepción basada en el (sugerencias Cambios Artificial (ajeno al Alumnos que han Comprobación transferencia contexto escolar) la modificación. bajo CI) aprendizaje y la Artificial (ajeno al Procedimiento Estudiantes de bajo basado en rendimiento sugerencias académico (Campione y Brown) Pretest-aprendizaje mediado inicial-prueba estática de mantenimiento y mantenimiento y transferencia mediados. del empleo de pruebas tradicionales, la comprobación se sitúa dentro de unos Una medida de la zona de desarrollo próximo. ámbitos concretos. Tabla 1. Modelos de evaluación dinámica Página 97 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Por último la propuesta que desarrollo Gardner sobre las evaluaciones dinámicas, en la que tiene en cuenta los puntos fuertes de los anteriores planteamientos expuestos en este proyecto, pero ya más en concreto de las inteligencias múltiples, tiene los siguientes principios fundamentales. 1. Las pruebas estandarizadas miden solamente una pequeña parte de la gama completa de habilidades de un alumno. 2. Se hacen por medio de evaluaciones realistas de los desempeños de la persona en los muchos tipos de tareas, actividades y experiencias de la vida real que se asocian con cada inteligencia. 3. Una evaluación dinámica presupone la comprensión precisa del perfil de las inteligencias del alumno. La identificación precoz de las capacidades puede ser de gran ayuda a la hora de descubrir de qué tipo de experiencias pueden beneficiarse mejor los estudiantes; pero además, si un punto débil se identifica pronto, existe la oportunidad de atenderlo antes de que sea demasiado tarde. La evaluación temprana puede descubrir modos alternativos de cubrir el área correspondiente a alguna capacidad o proponer rutas alternativas. 4. Una técnica para averiguar la mayor o menor inclinación que un individuo muestra hacia una determinada inteligencia es exponerle a una situación lo suficientemente compleja como para que pueda estimular varias inteligencias, y comprobar hacia cuál de ellas se inclina y con qué grado de profundidad. 5. Informa de los resultados que nos ofrecen este tipo de pruebas como parte de un perfil individual de propensiones intelectuales, más que como un único índice de inteligencia o puntuación dentro de cada materia tradicional. Página 98 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 6. El objetivo es valorar los conocimientos y habilidades de los alumnos. 7. Este tipo de evaluación debe permitir diseñar perfiles individualizados para que cada alumno pueda aprender a su ritmo y según sus capacidades. 8. Se debe poner mayor énfasis de diagnóstico en el proceso de aprendizaje que en el producto. 9. Evaluar la competencia cognitiva de forma simple, natural y en el momento adecuado, en lugar de realizar evaluaciones externas y en momentos inoportunos. 10. No solo deben regirse por el modelo lingüístico o lógico-matemático, sino que se deben usar y diseñar instrumentos que valores directamente la inteligencia que está operando cuando se realizan determinadas tareas. 11. Disponer de un portfolio lo más amplio posible que consiga recoger la mayor cantidad de información del proceso de enseñanza procedente de las distintas situaciones, registros de evaluación, observaciones y opiniones de profesores y padres, estilos de trabajo, producciones de los alumnos, etc… 12. El procedimiento de evaluaciones debe ser sensible a las diferencias individuales, los niveles evolutivos y las distintas formas de habilidad. 13. Los instrumentos de evaluación deben resultar atractivos y entusiasmantes de manera que mantengan su interés y sigan motivados por obtener buenos resultados. 14. La evaluación tiene que ser aplicada por parte de los profesores, padres y orientadores, en provecho del alumno. A continuación se presentan una serie de ventajas de las evaluaciones dinámicas de las inteligencias múltiples propuesta por Gardner respecto de la evaluación psicométrica tradicional. Página 99 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Imagen 2. Eval. Estáticas vs Dinámicas 1 A modo de aglutinamiento y compendio de estas teorías de evaluación dinámica, se puede decir que los anteriores modelos analizados tienen en común los siguientes aspectos: 1. Todos los individuos tienen potencial para aprender cualquier cosa, algunos aprendizajes son más rápidos en unos que en otros. Página 100 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 2. La edad puede o no afectar la velocidad de aprendizaje. El cociente intelectual de los alumnos no es constante sino que varía según la cantidad de materia gris de nuestro cerebro, lo que depende de la etapa del adolescente. Por lo que es tan necesario despertar las conexiones sinápticas adecuadas en cada alumno para que su desarrollo intelectual sea óptimo. 3. Las personas varían en la manera en la que les gusta aprender. 4. Los individuos experimentan procesos de cambio continuos por los que en determinadas situaciones pueden presentar estrés o confusión. 5. El aprendizaje es más cómodo y efectivo cuando las condiciones del medio apoyan el intercambio abierto, el compartir opiniones y las estrategias de solución de problemas. 6. En el aula el maestro facilita el aprendizaje mediante la incorporación de la experiencia de los alumnos, las observaciones de los demás, y las ideas y sentimientos personales. Se les debe clarificar acciones y creencias para que puedan alcanzar sus propias metas. 7. La profundidad en el aprendizaje se incrementa cuando los nuevos conceptos y habilidades son útiles para afrontar necesidades o problemas actuales, lo que permite la inmediata aplicación de la teoría a la práctica. 8. El aprendizaje del alumno mejora cuando el alumno participa de manera activa en el proceso de evaluación. El uso de modelos dinámicos ayuda al maestro a mantener el interés y puede reafirmar conceptos sin ser repetitivo. Página 101 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS A continuación se ofrecen una serie de pautas sobre como evaluar cada una de las diferentes inteligencias. La inteligencia lingüística: Para la evaluación de esta inteligencia se utiliza la escala Likert de 1 a 4 para las habilidades de funciones primarias del lenguaje (narración, interacción con el adulto, investigación, descripción y categorización), habilidades de narración (estructura narrativa, coherencia temática, uso de voz narrativa, uso de dialogo, secuencias temporales, expresividad, nivel de vocabulario y estructura de la oración) y las habilidades referidas a la información (nivel de andamiaje, precisión del contenido, estructura del argumento, complejidad de vocabulario, nivel de detalles y estructuración de las frases). La inteligencia lógico-matemática: Para la evaluación de esta inteligencia se utiliza la escala Likert de 1 a 4 para las habilidades de pensamiento numérico, analítico, geométrico, estadístico, intuitivo, lógico-deductivo, critico, generativo (brainstorming) y lateral (creativo). La inteligencia naturalista: Para la evaluación de esta inteligencia se utilizan herramientas de medición como son la escala tipo Likert (ver (24)) de 1 a 4 para las habilidades de observación precisa, identificación de relaciones, formulaciones y comprobación de hipótesis, experimentación, interés por el conocimiento del mundo natural. (Ver Anexo 1). La inteligencia espacial: Para la evaluación de esta inteligencia se utiliza también la escala Likert de 1 a 4 para las habilidades de representación, exploración y talento artístico. Página 102 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS La inteligencia interpersonal: Para la evaluación de esta inteligencia se utiliza también la escala Likert de 1 a 4 en cuestionarios, para las habilidades de saber entender a la gente, ser una persona receptiva y empática, manejar situaciones de conflicto o estrés. La inteligencia intrapersonal: Para la evaluación de esta inteligencia se utiliza también la escala Likert de 1 a 4 en cuestionarios, para las habilidades de saber el estado personal, conocimientos de sentimientos propios, conocimientos de pensamientos positivos y negativos propios. La inteligencia musical: Para la evaluación de este tipo de inteligencia se utiliza la escala Likert de 1 a 4 para las habilidades de sensibilidad al tono, al ritmo y la capacidad musical. La inteligencia corporal: Para la evaluación de esta inteligencia se utiliza también la escala Likert de 1 a 4 para las habilidades de sensibilidad al ritmo, expresividad, control corporal y generación de ideas mediante movimiento. Inteligencia creativa: Para la evaluación de esta inteligencia se utilizan una serie de instrumentos como los que aparecen en la tabla siguiente. INSTRUMENTO Tests de pensamiento creativo Inventario de actitudes e intereses Inventarios de personalidad Juicio de los productos IDENTIFICACIÓN Getzels y Jackson (1962) Wallach y Kogan (1965) Batería SOI de Guilford (1965) TTCT de Torrance (1974) Test de creatividad de Corbalán (2003) Holland y Baird (1968) Martínez Beltrán y Rimm (1985) 16 PF de Catell y otros (1970) Escala de personalidad creativa de Gough (1979) Colangelo y otros (1992) Forma de evaluación del producto creativo del estudiante de Reis y Renzulli (1991) Página 103 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS En esta inteligencia hay que medir rasgos psicológicos como la fluidez (verbal, ideacional y asociativa), originalidad, elaboración, flexibilidad (espontánea y de adaptación), el producto creativo, el contexto donde se produce el producto creativo. Aunque se tenga el mayor cociente intelectual jamás observado no se tiene porque disponer completamente desarrollo en todas las facetas intelectuales tratadas anteriormente. Desde el entorno educativo se debe fomentar el desarrollo y la integración de las múltiples habilidades de los alumnos y hacerles partícipes de ello, trabajando de modo incansable y con una motivación inagotable. Para el trabajo diario se establece un portfolio para la medición de las inteligencias de los alumnos y por cada trimestre se establece también un portafolio de evaluación mediada con el alumno, como los siguientes. Imagen 3. Portafolio mediado 1 Página 104 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Imagen 4. Portafolio de evaluación 1 Página 105 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 4.7. REFLEXIONES FINALES Y CONCLUSIONES Este Trabajo Fin de Master, viene motivado principalmente por la experiencia vivida como alumno y docente en prácticas en un centro de características especiales en el que a la vista de los expedientes y las pruebas estáticas tradicionales los alumnos presentan un bajo nivel intelectual, pero que a la vista de la realidad no es tan así, como así lo demuestran sus desarrollos profesionales. Me ha servido para investigar e ir un poco más allá en todos los conocimientos adquiridos sobre los procesos de enseñanza y aprendizaje de las matemáticas, además de descubrir aspectos de la enseñanza de las matemáticas en otros países, metodologías, tecnologías y recursos que desconocía y que me servirán para estar más preparado a cualquier eventualidad en mi futuro como docente. La serie de actividades propuesta y la metodología de las inteligencias múltiples hoy en día está muy en boga y pienso que en un futuro no muy lejano los derroteros metodológicos de la enseñanza se encaminarán por estos cauces, y que además se tiene que invertir todavía muchísimo esfuerzo en las posibilidades que ofrece esta metodología sin menoscabar el contenido teórico de las actuales asignaturas, de modo que nos permita desarrollarnos como personas integras. Por otro lado, el planteamiento que se realiza en este Trabajo de Fin de Master sobre la creatividad como otra forma de inteligencia no está basado en ningún estudio, pero parte de un punto de vista en el que la creatividad debe ser el manto que envuelve las otras ocho inteligencias. Al igual que todavía no se conocen por completo las interconexiones que existen entre las diferentes partes del cerebro y por tanto entre las inteligencias del ser humano, la creatividad tampoco sabemos cómo les afecta, pero si existen experiencias que demuestran que los alumnos involucrados en procesos Página 106 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS creativos o con capacidades creativas más altas, demuestran un mayor desarrollo intelectual en todas las áreas. Por ello, y como hay cosas que todavía obviamos, cabe preguntarse siguientes cuestiones sobre si, ¿la creatividad es una propiedad de los productos, de los procesos o de las personas?, ¿si la creatividad es un fenómeno personal o social?, ¿si la creatividad es una actividad de dominio general que es esencialmente igual en todos los contextos o es una actividad de dominio especifico que depende del contexto en cuestión? Así mismo, un punto de vista a considerar tras leer este Trabajo Fin de Master, es que la teoría de las inteligencias múltiples planteada, parece que tiene que ver mucho con el desarrollo por competencias que plantea PISA y los correspondientes currículos educativos de las diferentes comunidades españolas. Si bien es cierto, que se divide el conocimiento por habilidades y no por conocimientos adquiridos, esta teoría deja abierto un ancho campo metodológico todavía por descubrir y que debemos todavía desde mi punto de vista experimentar desde el mayor compromiso y no desde el mero hecho de cambiar la metodología porque la sociedad y los perfiles de los adolescentes hayan cambiado, sino por una mayor querencia por hacer que nuestro intelecto evolucione y sea más amplio, haciendo que los cerebros de nuestros alumnos se desarrollen de la forma más óptima acorde a ellos mismos. Por ello, es tan importante destacar a la hora de hacer pruebas metodológicas con esta teoría de enseñanza-aprendizaje, no dirimir entre alumnos más capaces o menos en unas inteligencias que en otras. Al igual que en el modelo de enseñanza tradicional, a un alumno se le puede dar mal una asignatura a una cierta edad y posiblemente con el desarrollo cognitivo de otros conocimientos a otra edad sea más apto para recibir esos conocimientos y por ello no ser menos hábil en esa destreza sino que la fecha en la que se le ha planteado no es la adecuada para el alumno. Por lo que Página 107 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS hay que intentar fomentar y motivar a todos los alumnos en la medida de lo posible y atendiendo al desarrollo necesario en cada uno de ellos, todas las inteligencias propuestas por Gardner, sin discriminar entre alumnos, es decir, pensar que todos somos capaces de todo, aunque a diferentes edades. Esto nos llevaría a pensar en un diseño del currículo diferente al actual en el que se dividen y escalonan los conocimientos por cursos según la edad de los alumnos, a otro en el que los alumnos se dividan por inquietudes o intereses en los que estén más predispuestos al aprendizaje, siempre asegurando al final de la etapa en el centro el mismo grado de conocimientos y habilidades. Un problema que puede surgir, desde mi punto de vista puede ser a la hora de disponer de profesores de dos o tres especialidades en un mismo aula sobre como coordinarse en la docencia y asegurar un aprendizaje significativo en los alumnos, para lo cual se deberán realizar las pruebas oportunas con los profesores más abiertos a este cambio y más aptos para su desarrollo antes de poner en marcha esta metodología. Pero ante todo, no se puede perder la oportunidad que nos ofrece este planteamiento y probar y arriesgarnos aunque los resultados no sean los que busquemos. Página 108 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 5. REFERENCIAS Y BIBLIOGRAFÍA (1): Objetivos Plan Estudios MP 13-14 Unirioja.pdf (2): Wikipedia_Aprendizaje.pdf (3): Wkipedia_Ken Robinson.pdf (4): Wikipedia_Conductismo.pdf (5): Wikipedia_John Broadus Watson.pdf (6): Wikipedia_Iván Pávlov.pdf (7): Wikipedia_Burrhus Frederic Skinner.pdf (8): Wikipedia_Innatismo.pdf (9): Wikipedia_Psicología genética.pdf (10): Wikipedia_Etología.pdf (11): Wikipedia_Psicologia cognitiva.pdf (12): Wikipedia: Constructivismo (pedagogía).pdf (13): Wikipedia_Neuropsicología.pdf (14): Wikipedia_Teoría de las inteligencias múltiples.pdf (15): Inteligencias múltiples en el CEJ. Proyecto educativo de centro catalán en base a proyectos utilizando la teoría de las inteligencias múltiples. http://youtu.be/W5qOhsUObCo http://venisis.blogspot.com.es/2014/05/utilizacion-de-la-teoria-de.html (16): Luis H Colon_El cerebro que aprende_Neuropsicología (17): Wikipedia_Edward Thorndike.pdf (18): Wikipedia_Educación matemática.pdf (19): Trayectorias de aprendizaje.pdf (20): Wikipedia_Wikipedia_Área de Broca.pdf Página 109 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS (21): Wikipedia_Wikipedia_Amusia.pdf (22): ITE_Indicadores y datos de las tecnologias de la información y comunicación en la educación en Europa y España.pdf (23): Universidad de Murcia_El test CREA, inteligencia creativa.pdf (24): Wikipedia_Escala Likert.pdf Las inteligencias en secundaria en Mexico.pdf Fuente del MEC. Datos del informe PISA 2014 – Resolución de problemas. http://www.mecd.gob.es/prensa-mecd/actualidad/2014/04/20140401pisa/galeria.html Articulo educativo. Las múltiples inteligencias matemáticas. ¿Cómo y para que cultivarlas? El educador.com. http://www.eleducador.com/home/matematicas/534-articulo-matematicas-lasmultiples-inteligencias-matematicas.html Aplicación de la teoría de inteligencias múltiples. Proyecto escuela con cerebro. http://escuelaconcerebro.wordpress.com/2013/05/05/inteligencias-multiples-enel-aula/ Punset y Howard Gardner sobre la teoría de Las Inteligencias Múltiples. http://www.rtve.es/alacarta/videos/redes/redes-inteligencias-multipleseducacion-personalizada/1270216/ Video presentación sobre la aplicación de las teoría de las inteligencias múltiples, realizado por Ikaia TV. Capítulo 0 Inteligencias múltiples en el siglo XXI SD.mp4. Video presentación sobre la aplicación de las teoría de las inteligencias múltiples en el Centro Montserrat, realizado por Ikaia TV. Capítulo 1 Escuelas Inteligencias Múltiples.mp4. Página 110 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Trabajo Fin de Master Profesorado. José Divasón Mallagaray. Universidad de la Rioja. Geometría integrada en una red social. Trabajo Fin de Master Profesorado. David Leunda San Miguel. Universidad de la Rioja. Innovación docente a través de las TIC. Trabajo Fin de Master Profesorado. Verónica Sierra Rodríguez. Universidad de la Rioja. Una radio interactiva a través del aprendizaje cooperativo. Trabajo Fin de Master Profesorado. Raquel Villar Pajarés. Universidad de la Rioja. Matemáticas y ajedrez. Título: La creatividad en el contexto escolar. Estrategias para favorecerla. // Autores: María Dolores Prieto Sánchez, Olivia López Martínez y Carmen Ferrándiz García. // Editorial: Pirámide. // Año de publicación: 2003. Título: Estimular las inteligencias múltiples. // Autores: Celso A. Antunes. // Editorial: Narcea. // Año de publicación: 2006. Título: Juegos para estimular las inteligencias múltiples. // Autores: Celso A. Antunes. // Editorial: Pirámide. // Año de publicación: 2005. Título: La educación del talento. // Autores: José Antonio Marina. // Editorial: Ariel. // Año de publicación: 2010. Título: Tesis doctoral. Evaluar y atender a la diversidad de los alumnos desde las inteligencias múltiples. // Autores: Pilar Ballester Martínez. // Institución: Universidad de Murcia. // Año de publicación: 2004. Título: La Inteligencia Emocional Evaluación en Aula.pdf. // Autores: Natalio Extremera Pacheco y Pablo Fernández Berrocal. // Editorial: Revista Iberoamericana de educación. Universidad de Málaga. // Año de publicación: _. Página 111 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Applets de Biología. Recursos sobre biología y geología en internet. Ministerio de Educación. http://recursos.cnice.mec.es/biosfera/profesor/recursos_applets.htm Recursos en línea sobre Applets. http://biosfera.wikispaces.com/Actividades Recursos en línea sobre Fislets. http://www.um.es/fem/Fislets/CD/ EDMODO. Plataforma virtual abierta para la enseñanza y el aprendizaje. https://www.edmodo.com/ Twiter. Plataforma de comunicación mediante mensajería instantánea. https://twitter.com/ Revista de divulgación científica. Cacumen. Página 112 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 6. APÉNDICES 1. Constructo: Cualquier entidad hipotética de difícil definición dentro de una teoría científica. Un constructo es algo de lo que se sabe que existe, pero cuya definición es difícil o controvertida. Son constructos la inteligencia, la personalidad y la creatividad, por ejemplo. 2. TAC: Tomografía axial computarizada. 3. PET: Tomografía por emisión de positrones. 4. Cliché: Se refiere a una frase, expresión, acción o idea que ha sido usada en exceso, hasta el punto en que pierde la fuerza o novedad pretendida, especialmente si en un principio fue considerada notoriamente poderosa o innovadora. 5. PISA: Programa Internacional para la Evaluación de Estudiantes. 6. OCDE: Organización para la Cooperación y el Desarrollo Económico. 7. OMS: Organización Mundial de la Salud. 8. PEC: Proyecto Educativo de Centro. 9. Feedback: Retroalimentación o dar respuesta a un determinado pedido o acontecimiento. 10. SOI: Structure of Inteligence. 11. E-Learning: Se denomina aprendizaje electrónico a la educación a distancia completamente virtualizada a través de los nuevos canales electrónicos, utilizando para ello herramientas o aplicaciones de hipertexto como soporte de los procesos de enseñanza-aprendizaje. 12. SCORM: Sharable Content Object Reference Model. Página 113 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7. ANEXOS 7.1 ANEXO 1: ACTIVIDADES DE LA UNIDAD DIDÁCTICA DE DERIVADAS DE 1º BACHILLERATO DE CIENCIAS SOCIALES. Actividades de introducción y motivación Son actividades de introducción de la unidad, en ellas se incluyen ilustraciones, casos de la vida real, noticias… que nos permitan establecer la importancia del contenido que vamos a enseñar a lo largo de la unidad y la utilidad práctica de dicho contenido. Actividad 1: Esquema Inicial de la Unidad Didáctica de Derivadas. En esta actividad de presentación se abordará de manera general todos los conceptos que se van a desarrollar durante la unidad didáctica, para que tengan claro el devenir de las clases. Se les facilitará a los alumnos una hoja con el esquema que se leerá en clase. Se propondrá por parte de los alumnos sus puntos de vista sobre la unidad y cuales pueden resultar de más interés. Actividad 2: Significado de la palabra “Derivar”. Se propondrá a los alumnos que piensen sobre este concepto para dar una definición del mismo, por parejas de dos. Página 114 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividad 3. Se realizarán una serie de ejercicios de límites con la intención de introducir y de acercar la idea de limite cuando x tiende a h, así como una serie de ejercicios que permitan repasar la idea de pendiente, de modo que en la clase de explicación del concepto de derivada puedan integrar los dos conceptos. Actividad 4: Crecimiento de una función en un intervalo. Relacionar el concepto de Tasa de Variación Media con el de Pendiente. Ofrecer el concepto teórico de Tasa de Variación Media: Actividad 5: Crecimiento de una función en un punto. Ofrecer el concepto teórico de Derivada. Actividades destinadas a la comprensión de conceptos para el desarrollo del conocimiento Son actividades de introducción de la unidad, en ellas se incluirán ilustraciones, casos de la vida real, noticias… que nos permitan establecer la importancia del contenido que vamos a enseñar a lo largo de la unidad y la utilidad práctica de dicho contenido. Actividad 1: Ejercicios de tasa de variación de media. Realización de actividades de aplicación de la tasa de variación media del libro, así como, ejercicios de interpretación gráfica de la misma. Se realizarán de manera conductista desde la pizarra inicialmente para después pasar a realizar en conjunto con los alumnos en la pizarra en la medida que el devenir de las clases lo permita. Página 115 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividad 2: Ejercicios de relación entre la tasa de variación media y la definición de derivada y su ampliación a las reglas de derivación. Se realizarán ejercicios de relación entre la tasa de variación media y la pendiente de una recta con la pendiente de la recta tangente a la curva en un punto, para desarrollar el concepto de derivada en un punto de manera intuitiva y cognitivista. Así como una serie de cuestiones relacionadas con el concepto de derivada y lo que significa para los alumnos, a priori. Explicación de la relación entre continuidad y derivada de una función. Actividad 3: Derivaciones simples. Se trata de realizar ejercicios de derivación simples desde el orden de derivación, progresando hasta los más complicados de cada tipo por separado (potenciales, exponenciales, logarítmicas, trigonométricas e inversas trigonométricas). Posteriormente se ampliarán todos los ejercicios con la regla de la cadena. Se mandarán todos los días ejercicios para la realización individual en casa que se corregirán al día siguiente. Actividad 4: Representación gráfica de funciones. Se realizará una clase de introducción de los conceptos previos de la representación gráfica de manera intuitiva, de modo que a través de una serie de gráficas que se proyectarán en el proyector, se trata de que los alumnos comenten los conceptos previos de las mismas y se consigan sacar los conceptos nuevos de un modo dialogado con una puesta en común, además de darle sentido real a las gráficas estudiadas. Se entregarán ejercicios resueltos de representación gráfica en caso de que no de tiempo de completar todos. Página 116 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS A continuación, se procederá a la exposición de un esquema con todos los conceptos teóricos de la representación de gráficas con ejercicio simple ejemplificante. Se irán realizando ejercicios de representación gráfica por orden de dificultad según sea el devenir de las clases y la comprensión del alumnado hasta llegar a la representación de asíntotas oblicuas de diversas maneras y el estudio de la monotonía y la curvatura. Se entregarán ejercicios de ampliación complementarios a los del libro, para que los alumnos puedan seguir desarrollando sus conocimientos en casa. Actividad 5: Ejercicios de optimización. Al finalizar este bloque de contenidos se introducirá el concepto de optimización relacionándolo con el de la búsqueda de puntos críticos en la representación gráfica, así como, con los conceptos de beneficio, pérdidas, coste, ganancias desarrollados en este bachillerato. NOTA: Todo el contenido que se entregará a través de la página web, se irá copiando en la pizarra y cada alumno en su cuaderno de clase, de manera que tengan de su mano y letra los contenidos de la unidad didáctica para que puedan interiorizarlo mejor. Página 117 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividades de adquisición o mejora de destrezas y de ampliación Este tipo de actividades tiene como objetivo ir más allá del currículo en la medida en la que se pueda, proponiendo nuevos métodos de resolución así como una visión más global de los conceptos aprendidos de manera que los alumnos puedan indagar en nuevos conocimientos, que les puedan servir para un futuro. En la medida de lo posible se intentará hacer ver la posibilidad de llegar a la primitiva de una función de manera que adquieran al menos de manera intuitiva el concepto de integral. En la medida de lo posible se introducir diferentes métodos de resolución de asíntotas oblicuas diferentes a los típicamente vistos en los libros de texto. En la medida que se pueda se intentará llegar a ejercicios de optimización en los que necesiten diseñar la formula a estudiar a partir de una contextualización y serie de datos de partida. Página 118 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Trabajos prácticos Se tiene previsto la realización de una serie de actividades individuales en cada bloque de contenidos de esta unidad, que los alumnos deberán realizar de manera individual y que deberán presentar (bien on-line o de modo manuscrito), al finalizar la unidad didáctica. Estas actividades procederán íntegramente del libro. Trabajos en grupos En esta unidad didáctica no se contempla la realización de actividades en grupo, debido al escaso tiempo del que se dispone normalmente para el desarrollo del curso. No obstante si el desarrollo de las clases lo permite o si existe la posibilidad de enlazar alguna actividad del centro con la unidad didáctica en concreto, se intentará motivar a los alumnos a que realicen un trabajo personal de poca extensión en relación con la unidad. Actividades de recuperación Se realizará una clase de recopilación de contenidos con una actividad integradora con un ejercicio sencillo de cada concepto teórico con su aplicación de manera participativa y dialogada. Para cerrar la unidad didáctica se tratarán una serie de puntos clave donde suelen cometer fallos los alumnos de cara a la prueba final de la unidad didáctica. También está previsto la realización de una serie de trabajos prácticos individuales, que permitan recuperar nota a aquellos alumnos que están cercanos al aprobado, en la medida que el devenir de las clases lo permita y el trabajo e implicación de los alumnos lo requiera. Página 119 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividades de control y atención a la diversidad Debido a que la procedencia de los alumnos es tan diversa y diferente ya sea por su origen cultural, educativo o motivacional, se realizarán actividades de baja carga teórica pero con gran carga motivacional inicialmente, a través de las cuales se motivará a los alumnos que muestren interés por la unidad a realizar actividades de ampliación en relación con la unidad o búsqueda de nuevos contenidos en internet relacionados con la asignatura de los que durante las clases se hablará y se comentará para que el resto de los compañeros puedan adquirir también esos conocimientos. Los alumnos aventajados realizarán apoyo a sus compañeros en el devenir normal de las clases para ayudar en la compresión de los contenidos. Para los alumnos menos aventajados se recomendará que acudan a las horas de tutorías o durante los recreos a resolver dudas. Se probará a realizar un cuestionario on-line mediante Google Drive, de manera que nos permita avanzar en el uso de las TIC, así como método de comprobación directo y rápido de los contenidos teóricos. Página 120 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.2 ANEXO 2: RECURSOS UTILIZADOS Se utilizan a nivel general una serie de recursos que se detallan a continuación: Pizarra digital en las clases de 2º de ESO. Ordenador con proyector para la realización de actividades en la pizarra de manera dinámica. Recursos digitales on-line. Contenidos educativos digitales “Educarex”. http://conteni2.educarex.es/?a=42 Contenido virtual para suma de fracciones y números enteros. http://palmera.pntic.mec.es/~jcuadr2/fraccion/index.html Contenido virtual para la utilización de fracciones con animaciones. http://www.disfrutalasmatematicas.com/numeros/fraccionesmenu.html Pruebas virtuales de geometría. http://www.thatquiz.org/es-f/ Ejercicios sobre unidades de medida en Catalán. http://genmagic.net/repositorio/displayimage.php?album=2&pos=20 Ejercicios virtuales sobre unidades de medida en Francés. http://matoumatheux.ac-rennes.fr/cours/mesures/convlong.htm#CM2 Teoría y ejercicios virtuales sobre la ecuación de segundo grado. http://www.genmagic.net/educa/mod/resource/view.php?inpopup=tru e&id=83 Teoría y ejercicios virtuales sobre las identidades notables. http://www.genmagic.net/educa/mod/resource/view.php?inpopup=tru e&id=123 Juego virtual sobre criterios operaciones en operaciones sencillas. http://www.genmagic.net/mates4/jerarquia_opera_c.swf Ejercicios virtuales sobre álgebra. http://wipas.wikispaces.com/Actividades+de+Algebra Ejercicios virtuales de Anaya sobre álgebra. http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/an aya1/datos/10/unidad_10.htm Ejercicios, juegos y videos sobre proporcionalidad. http://luisamariaarias.wordpress.com/matematicas/tema11proporcionalidad-y-porcentaje/ Video Disney Pato Donald sobre las Matemáticas. https://www.youtube.com/watch?v=-MTydDZWRMo Página 121 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Aulas Identificación de gráficas para 2º ESO. http://udisatenex.educarex.es/gseex/matematicas/Funciones_Afines/ Juegos virtuales sobre gráficas. http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/an aya1/datos/14/01.htm Ejercicio de interpretación gráfica de Anaya. http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/an aya1/datos/14/05.htm Calculadora virtual para aprender el manejo de las funciones más simples. http://conteni2.educarex.es/mats/11873/contenido/modulos_compilad os/calculadora.swf Ejercicios de derivación en Francés. http://www.mathematiquesfaciles.com/cours_maths/exercices-demaths-sur-derivation GeobegraTube para la realización de ejemplos de representaciones gráficas y derivadas. http://www.geogebratube.org/?lang=es Video historia y matemáticas (Euler). Youtube https://www.youtube.com/watch?v=Bu52Q2HAVHs Video sobre las pompas de jabón y la tensión superficial. Youtube. https://www.youtube.com/watch?v=t6lNOQYprXo de laboratorio para el desarrollo de una clase con los alumnos de 1º ESO de compensatoria, con diferentes materiales de medición de peso, volumen y longitud, para el desarrollo de una clase sobre unidades de medida. Aulas tradicionales con pizarra tradicional. Libro y cuaderno tradicional. Libros de apoyo escolar para 1º de la ESO. Material educativo de tipo informático con el software Geogebra, con los alumnos de 1º de Bachillerato para el desarrollo de ejemplos de gráficos. Aula virtual para la puesta a disposición del alumnado del material adecuado para el desarrollo de la asignatura. Página 122 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Material de apoyo para el seguimiento de la asignatura y resumen de contenidos creados por el profesor de las asignaturas para los cuatro grupos de clase. Página 123 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.3 ANEXO 3: RECURSOS Y MATERIALES DE APOYO A LA DOCENCIA CARÁCTER TIPOS VALOR DIDÁCTICO Libro de texto Proporcionar al alumno una guía durante el proceso de aprendizaje de las matemáticas que será reforzado con el resto de recursos utilizados. Software informático Uso de software informático como GeoGebra, XLogo y Cabri II proporcionan al alumno una mejor oportunidad de abstracción y comprensión de los conceptos de la UD que requieren de ser visualizados. Material de dibujo Desarrolla la creatividad y es de gran apoyo en la consecución de los objetivos 1, 4 y 7 y competencias CCA, CAA y CAIP. Calculadora Ayuda al alumno a ejecutar operaciones tediosas y poder comprobar resultados obtenidos de manera rápida. Contribuye a los objetivos 2, 3, 5 y 6 y las competencias CAIP, CAA y CTID . Buscadores de internet Ayudan al logro de los objetivos 1, 2 y 7, además de las competencias CTID, CCA y CAIP . Consulta en libros bibliográficos Ayudan al logro de los objetivos 1, 3, 4, 5, 6 y 7, además de las competencias CTID, CCA y CAIP. Prensa Brinda la oportunidad de relacionar el tema con casos reales y despertar la curiosidad por este medio de información. Contribuye al logro de los objetivos 2, 4 y 5, además de las competencias CCA, CTID, CAA y CAIP. Cámaras de fotos El alumno identifica los contenidos en imágenes de la vida real. Contribuye en la consecución de los objetivos , además de las competencias CAA, CCEMF, CTID y CAIP. Básicos Complementarios Auxiliares Página 124 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS CARÁCTER TIPOS VALOR DIDÁCTICO Cuaderno de problemas Se utilizaría para desarrollar actividades de ampliación. Puede servir como herramienta para la atención a la diversidad si disponemos de cuadernillos de distintos niveles. Editor de texto Resulta de utilidad en la presentación de cualquier actividad. Contribuye al desarrollo de todos los objetivos, además de las competencias CAA, CCA, CTID y CL. Sonómetro Resulta de utilidad en la recogida de datos del ámbito real del centro para su posterior análisis. Contribuye al desarrollo de los objetivos 2, 4, 5 y 6, además de las competencias CTID, CCEMF y CAA. Pizarra digital Resulta de gran apoyo en la resolución de ejercicios de aplicaciones dinámicas que pueden contribuir en la consecución de todos los objetivos, además de las competencias CTID, CAA, CCA, CL. Página 125 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.4 ANEXO 4: TEMPORALIZACIÓN DE SESIONES UNIDAD DIDÁCTICA DE 1º BACH SESIONES CONTENIDOS 1º Sesión Introducción histórica. Utilidad de las derivadas. Aplicaciones en el mundo real. Introducción de fórmulas de tasa de variación media. Tarea ejercicios de TVM. 2º Sesión Corrección de ejercicios de TVM. Definición e interpretación geométrica de la definición de derivada mediante pizarra y Geogebra. Tarea ejercicios de definición de derivada. 3º Sesión Corrección de ejercicios de definición de derivada. Búsqueda de la ecuación de la recta tangente a la curva en un punto, a partir de su definición y ecuación punto pendiente y a partir de su interpretación geométrica. Tarea ejercicios de recta tangente a la curva en un punto. 4º Sesión Corrección de ejercicios recta tangente a curva. Realización de ejercicios de recopilación de TVM y definición de derivada. Se manda de tarea de unidad a entregar al final de la unidad de manera individual, una serie de 6 ejercicios entre los cuales hay ejercicios sobre TVM, definición de derivada y obtención de recta tangente a curva, puntuables para la evaluación. 5º Sesión Introducción y adaptación de conceptos a las reglas de derivación directa. Operaciones básicas de derivación y potencias. Tarea ejercicios derivación de operaciones básicas con potencias. 6º Sesión Corrección de ejercicios del día anterior. Introducción de reglas de derivación exponencial. Tarea ejercicios de derivación exponencial. 7º Sesión Corrección de ejercicios del día anterior. Introducción de reglas de derivación logarítmica. Tarea ejercicios de derivación logarítmica. 8º Sesión Corrección de ejercicios del día anterior. Introducción de reglas de derivación trigonométrica e inversa trigonométrica, así como la ampliación en todos los tipos de derivación a la regla de la cadena. Tarea ejercicios de derivación trigonométrica. 9º Sesión Corrección de ejercicios del día anterior. Introducción intuitiva de gráficas mediante Geogebra a partir de ejemplos de la vida real para comentarlos entre todos e intentar sacar las características fundamentales. Tarea ver gráficos ofrecidos en el libro para comentar al día siguiente. Página 126 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS SESIONES CONTENIDOS 10º Sesión Introducción de los puntos a analizar en una gráfica tanto polinómica como racional. Realización de un ejemplo sencillo y rápido. Tarea ejercicio sencillo de representación de grafica del libro (cuentan con la solución). 11º Sesión Realización del ejercicio del día anterior. Entrega de hojas con diferentes funciones a representar. Tarea realización de una gráfica polinomica complicada. Tarea ejercicio representación gráfica polinomica. 12º Sesión Corrección de ejercicio del día anterior. Tarea realización de un ejercicio de representación de función racional sencilla. Tarea ejercicio de representación de función racional. 13º Sesión Corrección de ejercicio del día anterior. Tarea realización de ejercicio de representación de gráfico con asíntota oblicua y curvatura. 14º Sesión Corrección de ejercicio del día anterior. Tarea realización de ejercicio de representación de gráfico con asíntota oblicua y curvatura. 15º Sesión Corrección de ejercicio del día anterior. Introducción de la herramienta de optimización y su relación con las derivadas. Realización de un ejemplo. Entrega de hojas de ejercicios de PAU y de libros sueltos recopilados. Tarea realización de ejercicio de optimización sencillo. 16º Sesión Corrección de ejercicio del día anterior. Realización de ejercicios complicados (sacar función a derivar) sobre optimización. Tarea realización de ejercicio complicado de optimización. 17º Sesión Corrección de ejercicio del día anterior. Repaso de un ejercicio de cada tipo visto. Resumen de puntos clave y dudas entre todos. Comentarios sobre trabajos individuales. 18º Sesión Prueba de Unidad Didáctica de Derivadas y sus aplicaciones Página 127 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.5 ANEXO 5: ACTIVIDADES DE TIPO JUEGOS Los juegos se deben utilizar solo cuando la programación lo haga posible y solo cuando se constituyan en un auxilio eficaz al alcance de un objetivo dentro de esa programación. En cierto modo, la elaboración del programa debe estar precedida del conocimiento de los juegos específicos y en la medida en que estos aparezcan en la propuesta pedagógica, deben ser aplicados siempre con el suficiente espíritu crítico como para mantenerlos, modificarlos o sustituirlos por otros si quedan lejos de esos objetivos. Por lo tanto, el juego solo tiene validez si se utiliza en el momento oportuno y ello está determinado por su carácter de reto, por el interés del alumno y por el objetivo propuesto. Jamás se debe introducir antes de que el alumno muestre madurez para superarlo y nunca cuando el alumno muestre cansancio por la actividad o tedio por los resultados. Como utilizar los JUEGOS. Existen cuatro elementos que justifican y en cierta forma condicionan la aplicación de los juegos. Esos elementos no se gradúan por la importancia y deben tenerse presentes con independencia del orden en que se presentan. Son los siguientes: 1. Capacidad de constituirse en un factor de autoestima para el alumno: Los juegos muy fáciles o cuya solución se sitúa por encima de la capacidad resolutiva del alumno provocan su desinterés, y lo que es peor, su baja estima, asociada a una sensación de incapacidad o fracaso. En ese sentido, es importante que el profesor pueda organizarlos de tal forma que sean retos intrigantes o estimulantes, pero posibles de ser concretados por los alumnos, de modo individual Página 128 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS o en grupo. Ese nivel de dificultad ideal no es una parte inherente del juego, sino que procede de la agudeza y de la perspicacia de observación del profesor que puede dar algunas “informaciones nuevas” facilitadoras cuando el juego es muy difícil, o crear estrategias más complejas, si lo juzga de fácil solución. El refuerzo positivo expresado en gestos, palabras y otros símbolos debe siempre encerrar la actividad y continuar con una entusiasta invitación para otro juego, la próxima vez. 2. Condiciones psicológicas favorables: El juego jamás puede surgir como “trabajo” o estar relacionado con alguna forma de sanción. Al contrario, es esencial que el profesor lo utilice como instrumento para combatir la apatía y como medio de inserción y desafío grupal. El entusiasmo del profesor y la preparación de los alumnos para un “momento especial propiciado por el juego” constituye un recurso insustituible en el estímulo para el alumno. Los juegos deben ser cuidadosamente introducidos y la posición de los alumnos debe estar claramente definida. 3. Condiciones ambientales: El ambiente es fundamental para el éxito de los juegos. El espacio necesario para la manipulación de las piezas es imprescindible, así como su cuidadoso empaquetado y organización, la limpieza de la mesa o incluso el lugar que el alumno utiliza para esa actividad. 4. Fundamentos técnicos: Un juego nunca debe ser interrumpido y, siempre que sea posible, el alumno debe ser estimulado para buscar sus propios caminos. Además de eso, todo juego necesita tener Página 129 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS siempre un comienzo, intermedio y final, y no ser programado si existen dudas sobre las posibilidades de concluirlo. A modo de orientación para el desarrollo de todos los juegos que se proponen a continuación, es bueno administrarle al niño de manera discontinua pero periódica los siguientes consejos: 1. Adminístrate tu tiempo para estudiar, jugar, salir con los amigos, ver la televisión. Puedes ayudarte de una agenda. 2. Evita respuestas monosilábicas en las actividades diarias y pídele la opinión sobre la actividad. Anímale a pensar en el porqué y el cómo. 3. Intenta encontrar las ideas principales de la actividad. 4. Sopesa y compara toda la información disponible a la hora de comunicar un resultado de una actividad. 5. Establece enlaces de nuevas ideas o descubrimientos con las ya conocidas. 6. Fíjate unas metas para tus proyectos. 7. Hazte preguntas como ¿ésto es corriente?¿puede ser demostrado?¿es un hecho o una opinión?¿es fiable?¿esta es mi opinión o la opinión de otros que asumí?. De este modo se incita al alumno a hacer indagaciones. 8. Expón los pasos para el tratamiento de un problema. Identificarlo, planearlo, ejecutarlo, evaluar resultados. 9. Oriéntate en el mapa de esta ciudad. 10. Prueba a escribir y expresar tu idea de algo mediante un lenguaje no cotidiano, musical, poema, sonidos… 11. Busca siempre el porqué de los hechos conocidos. Página 130 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS A continuación se hacen una serie de propuestas de actividades a desarrollar en clases de secundaria, para la aplicación de la teoría de las inteligencias múltiples en relación a la inteligencia matemática. Juego dentro del área de Lengua que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Descifra el mensaje. Habilidad matemática a enseñar: Pensamiento lógico-deductivo. Estimulaciones utilizadas: Curiosidad. Preparación: El profesor crea un conjunto de signos que simbolizan las letras del alfabeto y números naturales. Existe una relación que el profesor debe crear entre las diferentes letras y números. Cada signo debe presentarse como una secuencia lógica de modo que estimule la deducción del alumno para llegar a su descubrimiento. Desarrollo: Explicando los procedimientos que los alumnos, generalmente repartidos en tríos o en grupos no superiores a cinco personas, deben desarrollar para alcanzar y explorar la capacidad de deducción, redactar mensajes que estas operaciones y el uso de distintas habilidades operatorias según el nivel de dificultad que el profesor estipule. Por ultimo deben componer la frase entre los diferentes grupos de la clase y debatir sobre los métodos de resolución, así como del resultado obtenido y de la significación lingüística del mismo. Página 131 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Juego dentro del área de Música que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Diseño mi canción electrónica. Habilidad matemática a enseñar: Pensamiento analítico, generativo y creativo. Estimulaciones utilizadas: Canciones de ambiente del momento. Preparación: El profesor mediante el programa XLogo, diferentes canciones para exponer a los alumnos (el planteamiento de esta actividad supone al menos 2 semanas de tiempo con alumnos de bachillerato). Se prestará gran parte del código a los alumnos que deberán modificar en sus ordenadores personales de aula, en base a los criterios seguidos por el profesor de música. Desarrollo: La actividad se desarrolla en el aula de informática con un ordenador por persona y con instrumentos disponibles traídos del aula de música. Los alumnos deberán modificar los códigos correspondientes a las notas del pentagrama utilizado para la elaboración de la canción propia con el profesor de música. Al finalizar, se podría hacer una ampliación realizando los diferentes instrumentos de una canción de una orquesta para reconocer la belleza de la música con instrumentos reales y con instrumentos electrónicos. Página 132 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Juego dentro del área de Informática que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Dominó virtual. Habilidad matemática a enseñar: Capacidad para utilizar números de manera efectiva. Estimulaciones utilizadas: Comprobar hasta qué punto nos es útil el cálculo mental y en que nos puede ayudar las herramientas informáticas. Preparación: El profesor preparará una plantilla en excell que se compartirá en el ordenador de los alumnos distribuidos por grupos, compuesto por una serie de celdas (en forma de fichas de dominó) con números resultantes de una tabla madre y símbolos de multiplicación división, raíz. En otro lado de la tabla excell aparecen los resultados que deben obtenerse con las diferentes combinaciones de las fichas de dominó. Desarrollo: La actividad sigue las reglas de un juego de dominó, con los compañeros (parejas o grupos de tres, debe haber quien pruebe con el papel y quien pruebe mentalmente) montando las secuencias correspondientes. Una forma distinta de explorar el recurso es que el profesor anuncie el resultado y los alumnos busquen la operación correspondiente. Al finalizar la actividad se tratará de descifrar el código excell que ha diseñado el profesor y los alumnos por grupos desarrollarán el suyo propio. Página 133 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Juego dentro del área de Tecnología que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Los datos del reciclaje. Habilidad matemática a enseñar: Pensamiento analítico e intuitivo. Estimulaciones utilizadas: Conocer la realidad de nuestros consumos y vida diaria. Preparación: Se trata de que a partir la basura generada en el patio del colegio, a través de la recogida de los alumnos de clase, se analice cada componente de basura para comprobar su influencia en el ambiente y realizar un análisis a futuro mediante gráficas y métodos analíticos. Desarrollo: El profesor preparará el aula de manera que quede perfectamente distribuida para las tipologías de basuras que existen y unas tablas con los posibles componentes de las basuras en cantidad, en proporción y en densidad. Los alumnos a partir de estos datos y la información aportada sobre la contaminación y las medidas utilizadas hoy en día para combatirla por parte del profesor de tecnología, realizaran un análisis con graficas por grupos de 5 personas de la contaminación recogida y propuestas de mejora para esta basura recogida. Página 134 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Juego dentro del área de Francés que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: El acertijo francés. Habilidad matemática a enseñar: Pensamiento lógico-deductivo. Estimulaciones utilizadas: Motivación intrínseca por descubrir algo nuevo. Preparación: El profesor debe preparar una serie de acertijos matemáticos sencillos, redactados en francés que los alumnos deberán resolver y poner en común. Desarrollo: Mediante la lectura sucesiva por parte de los alumnos de la clase separados en grupos de dos personas, se dará un pequeño espacio de tiempo para interpretar las informaciones con la ayuda del profesor de francés, para que se intente resolver el enigma y comunicar el resultado de forma matemática y en francés para debatirlo con los demás compañeros de la clase. Juego dentro del área de Ciencias Sociales que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: El censo electoral. Habilidad matemática a enseñar: Pensamiento estadístico y crítico. Estimulaciones utilizadas: Conocer la verdad de datos periodísticos. Preparación: El profesor creará una serie de hojas con los datos de diferentes censos electorales proporcionados por diferentes fuentes. Los alumnos con la ayuda de ciertas fórmulas matemáticas expuestas irán relacionando los diferentes datos expuestos por cada fuente, para descubrir la realidad de los datos expuestos y su influencia en la sociedad. Página 135 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Desarrollo: Ofreciendo los diferentes parámetros estadísticos que suelen utilizarse para la medición de los resultados electorales, se trata de que los alumnos en grupos e 5 personas, desarrollen un planteamiento de los puntos clave del cálculo estadístico de cada fuente y de los fallos generados o no, para después poner en común junto con toda la clase y analizar las influencias de estas informaciones en la sociedad. Juego dentro del área de Ciencias Naturales que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Las matemáticas del bosque. Habilidad matemática a enseñar: Pensamiento geométrico. Estimulaciones utilizadas: Relacionarse con el entorno y con la naturaleza. Preparación: El profesor crea un conjunto de fotos de diferentes plantas y aspectos de la naturaleza susceptibles de ser interpretados geométrica y analíticamente. Cada foto debe presentarse por nivel de dificultad según una secuencia lógica de modo que estimule la indagación y el cuestionamiento interno del alumno para llegar a su descubrimiento. Desarrollo: Ofreciendo información sobre los diferentes orígenes de diversos aspectos naturales y repartiendo las fotos a grupos de tres personas, los alumnos con la ayuda del profesor deben descubrir que aspectos matemáticos se encuentra en las fotos. A partir de las mismas crearán dibujos por ellos mismos de las posibilidades que ofrecen las matemáticas en los diferentes aspectos de la naturaleza. Por último los alumnos realizarán una exposición de sus creaciones con las explicaciones correspondientes en los murales del centro. Página 136 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Juego dentro del área de Educación Física que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: El diagnóstico médico. Habilidad matemática a enseñar: Pensamiento analítico y crítico. Estimulaciones utilizadas: Conocer nuestra salud. Preparación: El profesor de educación física preparará una serie de pruebas físicas y recogidas de datos con los diferentes medios médicos a los alumnos, para después analizar con la ayuda del profesor de matemáticas y establecer propuestas. Desarrollo: Ofreciendo información sobre los parámetros a medir y los varemos utilizados en cada uno de ellos, se trata de realizar un análisis mediante tablas de resultados por cada grupo de 5 alumnos, para después poner en común y establecer una serie de propuestas medicas saludables en consenso con el profesor de educación física con los compañeros. Página 137 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.6 ANEXO 6: ACTIVIDADES TIPO LABORATORIO VIRTUAL O PRESENCIAL La posibilidad de desarrollar laboratorios virtuales soluciona el problema de tiempo y recursos y permiten al alumno interaccionar con distintas experiencias prácticas, modificando las condiciones y desarrollando el interés investigador (Barneto y Gil, 2006). Por otro lado, en caso de no tener la posibilidad de utilizar los recursos informáticos se puede contemplar la realización de estas actividades en modo presencial. El estándar de utilización del e-learning con el que los docentes deben estar familiarizados para utilizar este tipo de recursos es SCORM. Este estándar es una manera de realizar unidades didácticas online de modo que garanticen una cierta calidad educativa, englobando a estudiantes, profesores y desarrollares informáticos, así como los conocimientos previos a su utilización eficaz. Buscan el empaquetamiento y secuenciación de recursos, la interoperabilidad de herramientas, el ahorro en inversión en aprendizajes adicionales y esfuerzos docentes extras. La elaboración, justificación y definición de las aplicaciones educativas está liderado en la industria del e-learning por la empresa IMS Global Learning Consortium. Las posiciones que los alumnos pueden adoptar frente a este tipo de actividades pueden ser las siguientes. Estilo pragmático: A los estudiantes les gusta rápidamente cuando los proyectos o ideas que se les presenta les atraen. Página 138 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Estilo activo: Los alumnos son entusiastas ante nuevas tareas, les gusta vivir nuevas experiencias y buscan constantemente realizar nuevas actividades. Estilo teórico: Los alumnos son personas lógicas, perfeccionistas y coherentes. Estilo reflexivo: Son prudentes, observadores y distantes con el resto de sus compañeros. A continuación se hacen una serie de propuestas de laboratorio a realizar en una clase de secundaria para el fomento y desarrollo de las inteligencias múltiples desde la perspectiva de las matemáticas. Laboratorio virtual dentro del área de Lengua que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Comenta la película, “La habitación de Fermat”. Habilidad matemática a enseñar: Pensamiento analítico y lógico-deductivo. Estimulaciones utilizadas: Utilización de recurso en línea a modo de chat mientras se observa la película. Puede ser vía EDMODO, vía blog independiente del profesor o vía Twiter. Preparación: El profesor comentará en clase una serie de aspectos matemáticos presentes en la película seleccionada a modo de introducción, para motivar al alumno a que durante el fin de semana visualice la película mediante un enlace enviado por el profesor la película, e indague sobre dichos aspectos que tendrán que comentar de manera on-line. Página 139 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Desarrollo: Los alumnos deberán buscar información previa acerca de los aspectos matemáticos vistos en clase para poder estar preparados para la película, a una hora estipulada se enviará el correo con el enlace a la película para que todos puedan verla al mismo tiempo y puedan comentarla también al mismo tiempo. De modo que se fomente el conocimiento sobre estos aspectos matemáticos además de incrementar su grado de análisis y lógica al interpretar la película en los diferentes tiempos, junto con la mejora en moderación y síntesis en la expresión a la hora de comentarla, que serán evaluados por el profesor de lengua correspondiente. Laboratorio virtual dentro del área de Informática que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: No se contempla la realización de ninguna actividad de en este ámbito ya que al tratarse de un laboratorio virtual se desarrollarán habilidades informáticas alrededor de las actividades. Laboratorio virtual dentro del área de Tecnología que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Utilización de un sonómetro y sus elementos matemáticos. Habilidad matemática a enseñar: Pensamiento geométrico, analítico, estadístico. Estimulaciones utilizadas: Practicidad de los elementos estudiados para saber el nivel de ruido que puede haber en una clase. Preparación: El profesor de tecnología debe dar unas orientaciones previas sobre los conceptos básicos de la utilización de un sonómetro y su utilidad y el profesor de matemáticas desarrollará los conceptos teóricos que conlleva el diseño de sonómetro. Página 140 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Por grupos de 5 personas se trata de medir los niveles de ruido del centro para realizar un análisis estadístico posterior. Desarrollo: Por grupos de 5 personas los alumnos se distribuirán los trabajos de medición con un sonómetro que se irá compartiendo temporalmente, para después subir los datos recogidos al blog, o EDMODO correspondiente y realizar un estudio de las mediciones estadístico de las mediciones, controlado y diseñado por el profesor de matemáticas. Laboratorio virtual dentro del área de Inglés que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Compartir la historia de nuestra comunidad matemática con alumnos de un centro de habla inglesa con el que se realizará un intercambio a mitad de curso. Habilidad matemática a enseñar: Pensamiento analítico, crítico y generativo. Estimulaciones utilizadas: Conocer nuevas personas en el extranjero. Preparación: Se trata de compartir una serie de recursos informáticos tanto por parte del centro extranjero como por nuestro centro, donde los alumnos por parejas (autóctono vs extranjero), puedan compartir opiniones sobre las historias y personajes históricos entorno a las matemáticas de su comunidad correspondiente. Desarrollo: Los profesores de matemáticas e inglés correspondientes de ambos centros, se encargarán de preparar el entorno virtual y controlar el acceso, utilización y conclusiones llegadas por cada grupo de alumnos, para posteriormente realizar un trabajo conjunto cuando se realice el intercambio de exposición en cada centro. Se Página 141 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS deberán moderar las conversaciones de modo que no se comentan demasiados errores lingüísticos e históricos, a la vez que guiando la indagación de los propios alumnos. Laboratorio virtual dentro del área de Ciencias Sociales que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Escalas y geometrías utilizadas en los planos. Habilidad matemática a enseñar: Pensamiento geométrico. Estimulaciones utilizadas: Interpretación de planos de lugares cercanos al entorno del centro para una posterior actividad de orientación con el profesor de educación física. Preparación: El profesor de ciencias sociales en colaboración con el profesor de matemáticas desarrollarán diferentes ejercicios virtuales de interpretación de distancias y escalas sobre fotos de mapas mediante el software Geogebra, descargados del catastro. Desarrollo: Ambos profesores ofrecerán una clase previa de motivación de utilización de los mapas y su representación en papel y la utilidad de las escalas en cada caso. Por grupos de tres, los alumnos accederán a la aplicación virtual donde tendrán disponibles una serie de archivos en Geogebra y fotos descargadas del catastro, que deberán interpretar y responder a una serie de preguntas. Laboratorio virtual dentro del área de Ciencias Naturales que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Applet sobre los genes. Habilidad matemática a enseñar: Pensamiento estadístico. Página 142 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Estimulaciones utilizadas: Probar las combinaciones de genes lo que pueden resultar. Preparación: Los profesores de ciencias naturales y matemáticas, preparan un entorno virtual adecuado para probar las diferentes combinaciones de genes que se pueden dar y que resultados pueden ocasionar, para posteriormente comparar con las estadísticas reales aportadas por el ministerio de sanidad. Desarrollo: Los alumnos por grupos de tres personas, realizarán las diferentes combinaciones de genes y rellenaran las tablas proporcionadas para hacer una estadística en función a la población de la ciudad del centro de los resultados posibles, para posteriormente compararla con los datos reales. Laboratorio virtual dentro del área de Educación Física que combina la inteligencia matemática con el resto de inteligencias múltiples. Nombre de la actividad: Músculos en un partido de baloncesto. Habilidad matemática a enseñar: Estadística de los músculos del cuerpo humano que más actúan en el cuerpo de jugador de baloncesto durante un partido. Estimulaciones utilizadas: Utilizar los datos y videos del último partido de baloncesto del equipo de la ciudad correspondiente. Preparación: Entre el profesor de matemáticas y educación física, prepararan una serie de videos explicativos sobre las zonas musculares utilizadas en cada movimiento en un partido de baloncesto, el video del último partido del equipo de la ciudad y unas tablas estadísticas de músculos utilizados y posibles efectos en cada caso, que los alumnos tendrán que rellenar. Página 143 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Desarrollo: Los alumnos por grupos de 3 personas se encargarán de diferentes zonas del cuerpo humano, que analizarán a través del aula virtual para rellenar en función a la formación recibida, las tablas estadísticas de utilización de cada musculo, para comprobar que los efectos ocasionados se corresponden con la teoría y en caso contrario debatir sobre ello. La clase de matemáticas, de esta forma ya no consistirá de unos pocos estudiantes poniendo, a medias, atención a lo que él docente hace en la pizarra mientras los demás se ocupan en algo más divertido. Cada grupo experimental trabaja a su propio ritmo, con su propia dinámica, algunos con más dedicación y mejor integrados que otros. El trabajo del docente, de este modo, ahora es de orientación de los grupos, facilitando su trabajo, dando pistas y pautas, moderándolos. No todos los experimentos tienen que tener éxito ni en todos ellos se aprende lo mismo, pero los estudiantes están ocupados haciendo algo, muchas veces incluso divertido y retador, que siempre les hace desarrollar en cierto grado todas sus inteligencias. Página 144 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.7 ANEXO 7: ACTIVIDADES DE FOMENTO DE LA CREATIVIDAD MATEMÁTICA ¿Porque ofrecer actividades de desarrollo de la creatividad?.. Sabemos que tanto la mejora de la creatividad como de la inteligencia favorece el desarrollo potencial de los alumnos en todas las áreas. Además es preciso que desde la educación infantil, primaria y secundaria, se favorezca la generación y producción de conocimiento, y no la reproducción y memorización del mismo. El profesor debe enseñar al alumno a soltar su mente rígida y hacer actividades lo suficientemente variadas. Actividad 1: Un profesor tiene 32 alumnos en su clase todos menos 7 fueron a la piscina y estuvieron todo el día. ¿Cuántos se quedaron en clase ese día? Actividad 2: Intenta resolver el siguiente ejemplo: La mitad de la gente de una ciudad no aparece en la lista de teléfonos. Si seleccionas 300 nombres al azar de la lista de teléfonos. ¿Cuántos de estos no aparecerán en la lista? Actividad 3: Intenta resolver el siguiente ejemplo: Algunos animales nacen pareciéndose a sus SMERSCHS. Un insecto largo y delgado llamado palo se parece a las ramitas en las que vive. Un joven ciervo tienen un color marrón que se compara con la maleza de los árboles. En invierno las manchas blancas de los ciervos y la piel blanca del conejo se mezclan con el color de la nieve. ¿Qué significa SMERSCHS? Actividad 4: ¿Puedes solucionar el problema de Juan Luis? Juan Luis visita una isla donde viven dos tribus. Una tribu siempre dice la verdad. La otra tribu siempre miente. Los que dicen la verdad viven en el lado oeste de la isla y los que mienten viven en el lado este. Un nativo de la isla se supone que es el mensajero de Juan Luis. Antes de dar el trabajo, Juan Luis quiere averiguar si el Página 145 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS mensajero dice la verdad o no. Juan Luis ve a otro nativo caminando a lo lejos. Él le dice al mensajero “ve y pregunta a ese nativo de allí en qué lado de la isla vive. Cuando el mensajero regresa, responde: “dice que vive en el lado oeste de la isla”. Es el mensajero un mentiroso o cie la verdad? ¿Cómo puedes estar seguro? Actividad 5: El barril de cerveza. Un hombre adquirió cinco barriles de vino y 1 de cerveza. En el dibujo cada barril tiene marcado su contenido en litros. Vendió luego una cantidad de vino a un cliente y el doble de esta cantidad a otro, y ya sin que le quedara más vino, se guardó para si el barril de cerveza. El problema es, ahora, descubrir cuál es el barril de cerveza. ¿Puede usted determinarlo? Por supuesto, el hombre vendió los barriles tal como los había comprado, sin trasegar ni cambiar para nada sus contenidos. Actividad 6: Un hombre entro en un bar y pidió un vaso de agua. El camarero saco un arma, el hombre le dio las gracias y se fue. ¿Qué conclusión sacas? Actividad 7: ¿Es posible caer hacía arriba? ¿Es imposible catalogar lo incatalogable? Página 146 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividad 8: Trata de resolver el problema que tiene Carmen con los filetes. Carmen tiene una parrilla al aire libre suficientemente grande para poner dos filetes de carne. Ella, Mari Toñi y Ana están hambrientas. El problema es asar a la parrilla 3 filetes en el menor tiempo posible. Lleva 30 minutos asar ambos lados de un filete, porque cada lado necesita 10 minutos. Ya que se pueden cocinar 2 filetes a la vez, 20 minutos serán suficientes para tener dos filetes listos. En otros 20 minutos se asara el tercer filete y el trabajo se acabara en 40 minutos. Sin embargo, Mari Toñi descubrió un modo de ahorrar 10 minutos. ¿Cuál fue? Actividad 9: El caballero y la dama. Sentado una noche en la sala del castillo, Sir Hugh de Fortibus invitó a sus acompañantes a llenar sus copas y a oír el relato que deseaba contarles de sus aventuras de juventud cuando rescato del cautiverio a una noble señorita, que languidecía encerrada en una celda del castillo perteneciente al peor enemigo de su padre. La historia era conmovedora y cuando relató la huida final, escapando de todos los peligros y horrores del castillo de la Calavera, con la hermosa joven desvanecida en sus brazos, todos exclamaron: ¡Valeroso hidalgo!.. Pero Sir Hugh dijo que el valor mayor fue el ingenio que debió emplear para llegar hasta la celda de la joven. Sir Hugh trazó entonces un plano de las 35 habitaciones del castillo y pidió a sus amigos que descubrieran cuál de ellas ocupaba la joven. Dijo que si se empezaba en una habitación de la periferia y se atravesaban todas las aberturas una y no más de una vez, el recorrido terminaría forzosamente en la habitación buscada. ¿Puede usted dar con esa habitación? A menos que usted empiece en la habitación periférica correcta le será imposible atravesar todas las aberturas una y solo una vez. Pruebe dibujando la ruta con un lápiz. Página 147 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS Actividad 10: La bandera de los piratas: Esta bandera, de una banda de piratas de alta mar, indica con sus franjas cuantos hombres integraban la banda. Las doce franjas que aquí vemos nos dicen que la banda constaba de doce hombres. Cada vez que se incorporaba un nuevo hombre o uno era eliminado, se añadía una nueva banda o se quitaba una, según fuera el caso. ¿Puede usted descubrir cómo habría que cortar la bandera en la menor cantidad posible de partes que luego, vueltas a reunir den una bandera de solo diez franjas? No se permite desperdiciar ni un centímetro de la tela, y la bandera debe conservar su forma rectangular. Página 148 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.8 ANEXO 8: ESCALAS DE EVALUACIÓN DE INTELIGENCIAS MÚLTIPLES 7.8.1. Escala de evaluación de la inteligencia lingüística 7.8.2. Escala de evaluación de la inteligencia matemática Página 149 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.8.3. Escala de evaluación de la inteligencia naturalista 7.8.4. Escala de evaluación de la inteligencia espacial 7.8.5. Escala de evaluación de la inteligencia interpersonal Página 150 de 151 Álvaro Manuel Martínez Solanas TRABAJO FIN DE MÁSTER MÁSTER EN PROFESORADO, ESPECIALIDAD MATEMÁTICAS INTELIGENCIAS MÚLTIPLES EN CLASES DE MATEMÁTICAS 7.8.6. Escala de evaluación de la inteligencia intrapersonal 7.8.7. Escala de evaluación de la inteligencia musical 7.8.8. Escala de evaluación de la inteligencia corporal Página 151 de 151 Álvaro Manuel Martínez Solanas