2 FUNCIONES soluc hasta final OPCIÓN A

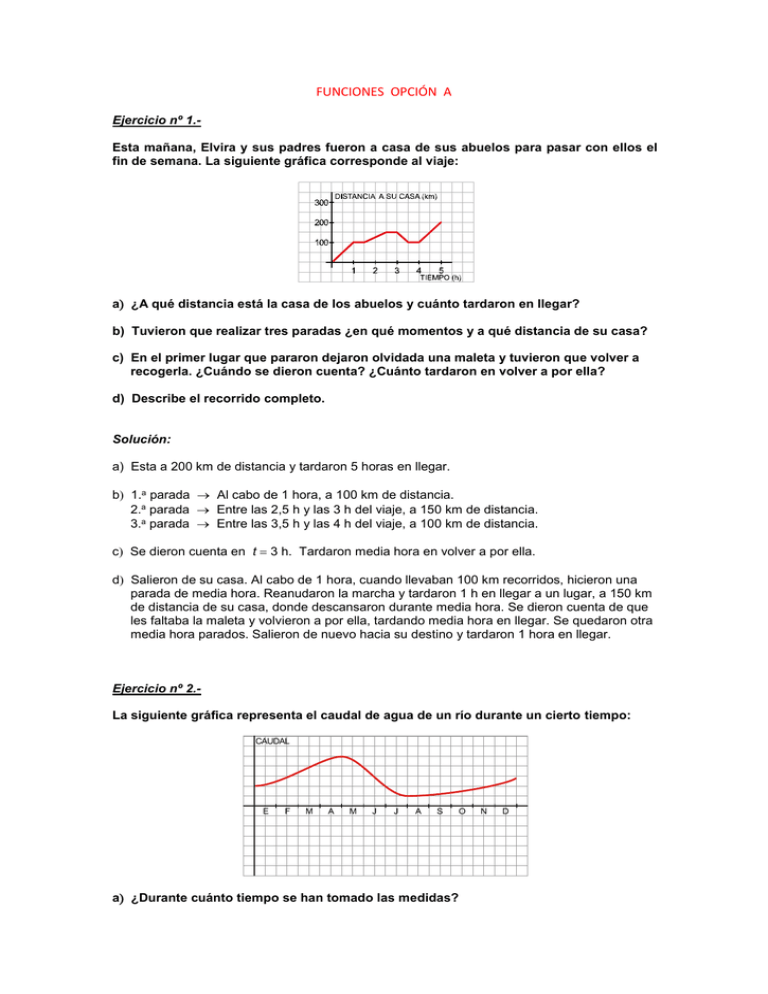
FUNCIONES OPCIÓN A
Ejercicio nº 1.Esta mañana, Elvira y sus padres fueron a casa de sus abuelos para pasar con ellos el
fin de semana. La siguiente gráfica corresponde al viaje:
a ¿A qué distancia está la casa de los abuelos y cuánto tardaron en llegar?
b) Tuvieron que realizar tres paradas ¿en qué momentos y a qué distancia de su casa?
c) En el primer lugar que pararon dejaron olvidada una maleta y tuvieron que volver a
recogerla. ¿Cuándo se dieron cuenta? ¿Cuánto tardaron en volver a por ella?
d) Describe el recorrido completo.
Solución:
a) Esta a 200 km de distancia y tardaron 5 horas en llegar.
b 1.a parada  Al cabo de 1 hora, a 100 km de distancia.
2.a parada  Entre las 2,5 h y las 3 h del viaje, a 150 km de distancia.
3.a parada  Entre las 3,5 h y las 4 h del viaje, a 100 km de distancia.
c Se dieron cuenta en t  3 h. Tardaron media hora en volver a por ella.
d Salieron de su casa. Al cabo de 1 hora, cuando llevaban 100 km recorridos, hicieron una
parada de media hora. Reanudaron la marcha y tardaron 1 h en llegar a un lugar, a 150 km
de distancia de su casa, donde descansaron durante media hora. Se dieron cuenta de que
les faltaba la maleta y volvieron a por ella, tardando media hora en llegar. Se quedaron otra
media hora parados. Salieron de nuevo hacia su destino y tardaron 1 hora en llegar.
Ejercicio nº 2.La siguiente gráfica representa el caudal de agua de un río durante un cierto tiempo:
a ¿Durante cuánto tiempo se han tomado las medidas?
b Describe el crecimiento y el decrecimiento del caudal.
c ¿En qué momento el caudal es máximo? ¿Cuándo es mínimo?
Solución:
a Durante 1 año.
b Creciente  Desde enero hasta abril y desde agosto hasta finales de año.
Decreciente  Desde abril hasta agosto.
c El caudal es máximo en abril y mínimo en agosto.
Ejercicio nº 3.Representa las siguientes funciones:
3
a) y   x  2
2
b 3x  2y  1
c y  2
Solución:
a Pasa por 0, 2 y 2, 1.
3x  1
2
Pasa por 1, 1 y 1, 2.
b) y 
c Paralela al eje X.
Ejercicio nº 4.Halla la ecuación de cada una de estas rectas:
a Pasa por los puntos P1, 2 y Q1, 8.
b Es paralela a 4x  2y  1 y pasa por el punto A0, 4.
Solución:
a) m 
8   2 
1   1

8  2 10

5
1 1
2
Ecuación puntopendiente:
y  8  5  x  1 
y  5x  3
b Paralela a 4x  2y  1  Tienen la misma pendiente.
4x  1
4
1
1
4x  2y  1  y 
  x   2x 
 m  2
2
2
2
2
Por pasar por A(0, 4)  n  4
La ecuación será: y  2x  4
Ejercicio nº 5.Un depósito contenía inicialmente 20 litros de agua cuando abrimos un grifo que arroja
un caudal de 10 litros por minuto dejamos el grifo abierto durante 6 minutos.
a Halla la ecuación de la recta que nos da el contenido de agua del depósito en función
del tiempo, desde que abrimos el grifo hasta que lo cerramos.
b Represéntala gráficamente.
c ¿Cuánta agua había en el depósito al cabo de los 5 minutos?
Solución:
a y  20  10x x desde 0 hasta 6 minutos
b
c Si x  5 minutos: y  20  10 · 5  20  50  70 litros
Ejercicio nº 6.Un ciclista sale a hacer ejercicio y pedalea a 15 km/h. Media hora más tarde sale en su
busca un motorista a 60 km/h.
a) Representa las funciones que dan el espacio recorrido por cada uno en función del
tiempo y escribe sus expresiones analíticas.
b) ¿Cuánto tardará el motorista en alcanzar al ciclista?
Solución:
a) Espacio recorrido por el ciclista (y )

  y  15 x
en función del tiempo, en horas, transcurrido (x ). 
Espacio recorrido por el motorista (y )

1

  y  60  x  
en función del tiempo, en horas, transcurrido (x ). 
2

Representamos ambas funciones:
1

y  15x
y  60  x    y  60x  30
2

x 0 1
y 0 15
x 12 1
y 0 30
b) El encuentro se producirá cuando ambos hayan recorrido la misma distancia, en este caso,
a los 40 minutos de salir el ciclista.
GEOMETRÍA OPCIÓN A
Ejercicio nº 1.Indica el valor de los ángulos que faltan en las siguientes figuras:
Solución:
a) Bˆ  50 ; Aˆ  180  50  130 ; Cˆ  130
b) Xˆ  90  37  53 ; Yˆ  90
c)   35 ;   2  35  70
Ejercicio nº 2.Observa la figura y dibuja el lugar geométrico de los puntos del plano que están a la
misma distancia de ambas rectas.
Solución:
El lugar geométrico obtenido es la bisectriz del ángulo Oˆ .
Ejercicio nº 3.Indica si son verdaderas o falsas las siguientes afirmaciones. En las que sean falsas,
explica por qué:
a En un poliedro simple, la suma del número de caras, el de vértices y el de aristas es
siempre igual a 2.
b El cubo y el dodecaedro son poliedros duales.
c El tetraedro es dual de sí mismo.
d La siguiente figura es un poliedro regular pues todas sus caras son triángulos
equiláteros:
Solución:
a Falsa. En un poliedro simple, el número de caras, más el número de vértices, menos el
número de aristas es siempre igual a 2 fórmula de Euler.
b Falsa. Son duales el cubo y el octaedro. También lo son el dodecaedro y el icosaedro.
c Verdadera.
d Falsa. Aunque todas sus caras sean polígonos regulares idénticos, en algunos vértices
concurren tres caras y en otros, cuatro.
Ejercicio nº 4.-
a La siguiente figura es un ortoedro con dos dimensiones iguales. ¿Cuáles son sus
planos de simetría?
b Dibuja una semiesfera e identifica sus ejes de simetría.
Solución:
a El ortoedro con dos dimensiones iguales es un prisma cuadrangular regular. Tiene cuatro
planos de simetría, uno por cada eje de simetría de sus bases cuadrados. Y otro plano
paralelo a las dos bases por los puntos medios de las aristas laterales.
b
Este eje pasa por el centro de la esfera y es perpendicular a la base de la semiesfera. Es
de orden infinito.
Ejercicio nº 5.Halla la longitud de la apotema de un hexágono regular de 8 cm de lado.
Solución:
Aplicamos el teorema de Pitágoras:
82  a2  42  64  a2  16  a2  64  16
a2  48  a  48  6,93 cm
Ejercicio nº 6.-
Halla la generatriz de un tronco de cono de 15 cm de altura en el que la longitud de la
base mayor es de 50,24 cm, y la de la base menor, 18,84 cm.
Solución:
Hallamos el radio de la base mayor:
2R  50,24 cm  R 
50,24 50,24

 8 cm
2
6,28
Hallamos el radio de la base menor:
2r  18,84 cm  r 
18,84 18,84

 3 cm
2
6,28
Por tanto:
g  h 2   R  r   152   8  3   250  15,81cm
2
2
Ejercicio nº 7.Halla el área de la parte coloreada:
AB  10 cm
CD  16 cm
AC  BD  5 cm
Solución:
 Área del sector circular 
r 2   82  60

 33,51cm2  A1
360
360
 Área del triángulo equilátero 
B h
2
h  82  42  64  16  48  6,93 cm
Área del triángulo 
 Área del trapecio 
8  6,93
 27,72 cm2  A 2
2
B  b  H
2
H  52  32  25  9  16  4 cm
Área del trapecio 
16  10  4
2
 52 cm2  A3
 Área del círculo  R2    22  4  12,57 cm2  A 4
 Área total  A1  A2  A3  A4  33,51  27,72  52  12,57  45,22 cm2
Ejercicio nº 8.Halla el área total de un tronco de pirámide de 9 cm de altura cuyas bases son
cuadrados de lados 15 cm y 12 cm, respectivamente.
Solución:
 Área de la base menor  122  144 cm2  A 1
 Área de la base mayor  152  225 cm2  A 2
 Área de una cara lateral 
Altura de una cara lateral:
B  b H
2
H  92  1,52  81 2,25  83,25  9,12 cm
Área de una cara lateral 
15  12  9,12  123,12 cm2
2
 Área de las cuatro caras laterales  4 · 123,12  492,48 cm2  A3
 Área total  A1  A2  A3  144  225  492,48  861,48 cm2
Ejercicio nº 9.Halla el volumen de cada uno de los siguientes cuerpos geométricos:
a El mayor cilindro inscrito en este prisma:
b
diámetro  7 m
Solución:
a  El radio de la base del cilindro coincide con la apotema de la base del prisma:
r 2  62  32  36  9  27
 La altura del cilindro coincide con la altura del prisma.
Volumen  r 2h    27  10  270  847,8 cm3
b  Radio de la esfera  7 : 2  3,5 m
Volumen 
4 3 4
R    3,53  179,50 m3
3
3
Ejercicio nº 10.Dibuja la figura, F, de vértices A3, 1, B1, 1, C1, 3 y D4, 3.
a) Obtén la figura, F , que resulta al aplicarle a F una traslación de vector t  7, 3 .
b Aplica a F ' una simetría cuyo eje sea el eje X.
Solución:
Ejercicio nº 11.-
a Describe un movimiento que transforme el triángulo F1 en el triángulo F2.
b Describe otro movimiento que transforme el triángulo F1 en el triángulo F3.
Solución:
a Simetría de eje e.
b) Traslación de vector t  2,  3 .
Hay otras soluciones.
Ejercicio nº 12.a Completa el siguiente friso e indica cuál es el motivo mínimo:
¿Cuál es la translación que transforma la figura en sí misma?
b Completa el siguiente rosetón e indica cuál es su orden de giro:
Solución:
a
La parte señalada, es el motivo mínimo.
Es invariante ante la traslación de vector u.
b
El orden de giro de este rosetón es 4.
ESTADÍSTICA Y AZAR OPCIÓN A
Ejercicio nº 1.a Haz una tabla de frecuencias en la que se refleje el número de veces que aparece
repetida cada una de las vocales en esta frase:
"La felicidad no consiste en tener siempre lo que se quiere, sino en querer siempre lo
que se tiene".
b Representa gráficamente la distribución anterior.
Solución:
a
VOCAL
a
e
i
o
u
fi
2
20
8
5
4
39
b
Ejercicio nº 2.Una empresa de publicidad hace una encuesta entre los lectores de una revista para
saber su edad aproximada y estudiar si deben anunciarse o no en esa revista. Las
respuestas obtenidas se reflejan en esta tabla:
EDAD
10 - 13
13 - 16
16 - 19
19 - 22
22 - 25
25 - 28
N. DE LECTORES
110
248
115
20
4
3
a Calcula la media y la desviación típica.
b Calcula qué porcentaje de lectores tiene menos de 19 años. ¿Qué observas?

c En otra encuesta realizada, la edad media era de 30,4 años y la desviación típica, de
3,2. Halla el coeficiente de variación en los dos casos y compara las dispersiones.
Solución:
a Hallamos la marca de clase, xi, de cada intervalo y hacemos la tabla:
2
Intervalo
xi
fi
fixi
fixi
10  13
11,5
110
1 265
14 547,5
13  16
14,5
248
3 596
52 142
16  19
17,5
115
2 012,5
35 218,75
19  22
20,5
20
410
8 405
22  25
23,5
4
94
2 209
25  28
26,5
3
79,5
2 106,75
500
7 457
114 629
Media:
x
fi xi 7 457

 14,914
n
500
Desviación típica:

fi xi 2
 x2 
n
114 629
 14,9142  6,83  2,61
500
b Por debajo de 19 años hay 110  248  115   473 lectores de 500. Luego:
473  100
 94,6
500
El 94,6% de los lectores tiene menos de 19 años. Por tanto, es una revista dedicada a
adolescentes.
c) C.V.1 
C.V.2 
1
2,61

 0,175
x1 14,914
2
3,2

 0,105
x2 30,4
La variación es algo mayor en el primer caso.
Ejercicio nº 3.En una urna hay 5 bolas, cuatro rojas y una azul. Sacamos una bola y anotamos su color.
Escribe el espacio muestral y califica cada suceso según su probabilidad:
TIPO DE SUCESO
SUCESO
Seguro
Sacar bola roja o azul.
Sacar bola azul.
Sacar bola verde.
Sacar bola roja.
Solución:
E  R, A
TIPO DE SUCESO
SUCESO
Seguro
Sacar bola roja o azul.
Posible
Sacar bola azul.
Imposible
Sacar bola verde.
Muy probable
Sacar bola roja.
Ejercicio nº 4.En un bombo se introducen 100 bolas numeradas del 0 al 99. Se extrae una bola al azar.
Calcula la probabilidad de que:
a La bola extraída contenga un número de dos cifras.
b El número extraído sea menor que 10.
Solución:
a) PS 
90
 0,9
100
b) PS 
10
 0,1
100
Ejercicio nº 5.Al lanzar 1 000 veces un dado se obtienen los resultados de la tabla:
a ¿Cuál es la frecuencia absoluta del 6?
b Calcula las frecuencias relativas de cada suceso.
c Estima la probabilidad de obtener par con ese dado.
Solución:
a 171
b
CARA
FREC.
FRECUENCIAS RELATIVAS
1
175
175/1 000  0,175
2
166
166/1 000  0,166
3
171
171/1 000  0,171
4
160
160/1 000  0,160
5
157
157/1 000  0,157
6
171
171/1 000  0,171
c) P PAR   fr PAR  
166  160  171 497

 0,497
1000
1000
Ejercicio nº 6.Hemos preguntado a 1 600 personas por el número de viajes que realizan anualmente
por motivos laborales y las respuestas fueron:
N. DE VIAJES
0
1
2
3
4 o más
N. DE PERSONAS
224
320
768
192
96
a Haz una taba de frecuencias.
b Expresa el número de personas en porcentaje y representa gráficamente la
distribución. ¿Qué porcentaje viaja como mínimo 2 veces al año?
Solución:
a xi  n. de viajes
xi
0
1
2
3
4
fi
224
320
768
192
96
b) No viajan en todo el año 224 personas de 1600
1 viaje al año lo hacen 320 personas

2 viajes al año los realizan 768 personas
3 viajes al año los hacen 192 personas

224  100
 14%
1600
320  100
 20%
1600


768  100
 48%
1600
192  100
 12%
1600
96  100
 6%
1600
Representamos los resultados obtenidos en un diagrama de barras verticales:
4 viajes anuales o más los hacen 96 personas

Los que viajan como mínimo 2 veces al año son los que viajan 2, 3, 4 o más veces, es decir,
48%  12%  6%  66% de los encuestados.