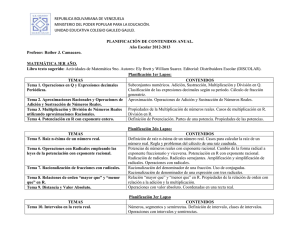
Propiedades de las operaciones

Propiedades de las operaciones



La operación de adición (+)
o se escribe
o es comutativa:
o
es asociativa:
o
tiene una operación inversa llamada sustracción:
o
igual a sumar un número negativo,
tiene un elemento neutro 0 que no altera la suma:
, que es
La operación de multiplicación (×)
o
se escribe
o
es conmutativa:
o
o
o
es asociativa:
es abreviada por yuxtaposición:
tiene una operación inversa, para números diferentes a cero, llamada división:
o
, que es igual a multiplicar por el recíproco,
tiene un elemento neutro 1 que no altera la multiplicación:
o
es distributiva respecto la adición:
ó
=
La operación de potenciación
o se escribe
o es una multiplicación repetida:
(n veces)
o
no es ni comutativa ni asociativa: en general
o
tiene una operación inversa, llamada logaritmo:
o
puede ser escrita en términos de raíz n-ésima:
y por lo
tanto las raíces pares de números negativos no existen en el sistema de los
números reales. (Ver: sistema de números complejos)
o
o
es distributiva con respecto a la multiplicación:
tiene la propiedad:
o
tiene la propiedad:
y
Orden de las operaciones
Para completar el valor de una expresión, es necesario calcular partes de ella en un
orden particular, conocido como el orden o precedencia de las operaciones. Primero se
calcula los valores de las expresiones encerradas en signos de agrupación (paréntesis,
corchetes, llaves), seguidas por multiplicaciones y divisiones, y seguidas finalmente por
las sumas, las restas, multiplicación y division.
Propiedades de la igualdad
La relación de igualdad (=) es:



reflexiva:
simétrica: si
transitiva: si
entonces
y
entonces
Leyes de la igualdad
La relación de igualdad (=) tiene las propiedades siguientes:





si
y
entonces
y
si
entonces
si dos símbolos son iguales, entonces, uno puede ser sustituido por el otro.
regularidad de la suma: trabajando con números reales o complejos sucede que si
entonces
.
regularidad condicional de la multiplicación: si
y no es cero, entonces
.
Leyes de la desigualdad
La relación de desigualdad (<) tiene las siguientes propiedades:




de transitividad: si
y
si
y
entonces
si
y
entonces
si
y
entonces
entonces
Regla de los signos
En el producto (cociente) de números positivos (+) y negativos (-) se cumplen las
siguientes reglas:
Simplificación de expresiones
Por: Melissa Murrias y Dra. Luz M .Rivera Vega
Una expresión es una colección significativa de números, variables y
signos de operación.
Ejemplos de Expresiones
2p + 5
4a - 6
3x-9+2
No son expresiones:
-4 - · c
No tiene sentido la resta y multiplicación
3b + 4= 9 El signo de "=" hace que no sea expresión. Esto es una
oración matemática.
Las variables son expresadas por letras, que tienen un valor
desconocido.
Ej: 4a
a es la variable
3b
b es la variable
El coeficiente es el número que está siempre localizado antes de la
variable; significa que el número está multiplicado por la variable.
Por ejemplo:
3a ; 3 es la coeficiente
-2c ; -2 es la coefieciente
x ; 1 es la coeficiente
Un término es un grupo de variables y coeficientes dividido por signos
de suma y resta.
Ej. 4x + 2y
4x es un termino
2y es un término
Término Semejante:
Un término es semejante a otro término si tiene la mismavariable o
variables con el mismo exponente o exponentes.
Ej. 2a + 3a
3b + 4d
3c + 3a
son términos semejantes
no son términos semejantes
no son términos semejantes
Simplificación de Expresiones:
La simplificación de expresiones consiste en agrupar los términos
semejantes y simplificarlo, si es posible.
Para simplificar la expresión se suman o restan los coeficientes de los
términos semejantes.
Por ejemplo:
4a - 3b + 2a
4a y 2a son términos semejantes
-3b no es término semejante
4a + 2a - 3b ( Se agrupan los términos semejantes)
6a - 3b
( Se resuelve la expresión)
Ejemplo:
2a + 4c
La expresión no se puede simplificar, ya que 2a y 4c no son
términos semejantes . Entonces, la expresión ya está simplificada.
Otro ejemplo:
3x + 2y - 9 + 4x +6
3x, 4x son términos semejantes
2y
-9, 6 son términos semejantes
Reagrupar términos semejantes:
3x + 4x + 2y - 9 + 6
7x + 2y - 3
Ejemplo:
2xy + 4z -9 + 2y _ xy
2xy y 2y No son términos semejantes. Para ser términos semejantes,
deben tener exactamente las mismas variables con los mismos
exponentes.
2xy, -xy
4z
9x
2y
son términos semejantes
2xy - xy + 4z - 9x+ 2y
xy + 4z - 9x + 2y
Ejercicios:
Determinar la coeficiente.
Coeficiente
1. 4x
____
2. -9z
____
3.
4.
x
-c
____
____
Determinar si es expresión o no.
1.
2.
3.
4.
3p + 6
4x + · 3
2a - 9
4x + 2 = 8
Determinar si son términos semejantes.
Sí o No
1. 4a , 3a
2. -2c , p
3. 3a , 3x
4. 4d , 3d
_____
_____
_____
_____
Simplifica las siguientes expresiones.
1. 4z + 3y - z
2. 9x + 6y - 9x
3. 4x + 5z + 4
4. 9xy + 3x - 2y
5. 4c + 5d - c + d
6. 9x - 7 + 3 + z
7. 4xy + 9x - 3y + z + xy
8.9p + 3q +r - 9 pqr
9. 4ws + 7wx - 3wx + 4
10. 9x - 3xyz + y + 7x + 5
Expresión de un radical en forma de potencia
Simplificación de radicales
Si existe un número natural que divida al índice y al exponente (o los exponentes)
del radicando, se obtiene un radical equivalente.
Reducción de radicales a índice común
1Hallamos el mínimo común múltiplo de los índices, que será el común índice
2Dividimos el común índice por cada uno de los índices y cada resultado obtenido se
multiplica por sus exponentes correspondientes.
Extracción de factores fuera del signo radical
Se descompone el radicando en factores. Si:
Un exponente es menor que el índice, el factor correspondiente se deja en el
radicando.
Un exponente es igual al índice, el factor correspondiente sale fuera del radicando.
Un exponente es mayor que el índice, se divide dicho exponente por el índice. El
cociente obtenido es el exponente del factor fuera del radicando y el resto es el
exponente del factor dentro del radicando.
Introducción de factores dentro del signo radical
Se introduce los factores elevados al índice correspondiente del radical.
Suma de radicales
Solamente pueden sumarse (o restarse) dos radicales cuando son radicales
semejantes, es decir, si son radicales con el mismo índice e igual radicando.
Producto de radicales
Radicales del mismo índice
Para multiplicar radicales con el mismo índice se multiplican los radicandos y se deja
el mismo índice.
Radicales de distinto índice
Primero se reducen a índice común y luego se multiplican.
Cociente de radicales
Para dividir radicales con el mismo índice se dividen los radicandos y se deja el
mismo índice.
Radicales de distinto índice
Primero se reducen a índice común y luego se dividen.
Potencia de radicales
Para elevar un radical a una potencia se eleva a dicha potencia el radicando y se deja
el mismo índice.
Raíz de un radical
La raíz de un radical es otro radical de igual radicando y cuyo índice es el
producto de los dos índices.
Operaciones con radicales
Producto de radicales
Cociente de radicales
Suma de radicales
Raíz de raíz