pendientes matemáticas 1º eso

ALUMNOS PENDIENTES DE MATEMÁTICAS DE 1º E.S.O.:
Los alumnos/as de E.S.O. que tengan la asignatura de Matemáticas de 1º
suspensa podrán recuperarla mediante la realización de un examen que
versará sobre los contenidos de 1º y que se realizará a finales del mes de
abril. Para poder practicar se presentan a continuación ejercicios de refuerzo
de los contenidos del curso a recuperar. Estos ejercicios tienen carácter
voluntario, pero pueden servir de referencia para preparar los contenidos del
curso.
E j er ci ci o s d e núm e ro s na t ur a les
1.Busca el término desconocido e indica su nombre en las
siguientes operaciones:
1. 327 + ....... = 1.208
2. ....... – 4.121 = 626
3. 321 · ....... = 32 100
4. 28.035 : ....... = 623
2.Busca el término desconocido en las siguien tes operaciones:
1. 4 · (5 + ...) = 36
2. (30 – ...) : 5 + 4 = 8
3. 18 · ... + 4 · ... = 56
4. 30 – ... : 8 = 25
3.Calcular de dos modos distintos la siguiente operaciones:
1. 17 · 38 + 17 · 12 =
2. 6 · 59 + 4 · 59 =
3. (6 + 12) : 3
4.Sacar factor común:
1. 7 · 5 – 3 · 5 + 16 · 5 – 5 · 4 =
2. 6 · 4 – 4 · 3 + 4 · 9 – 5 · 4 =
3. 8 · 34 + 8 · 46 + 8 · 20 =
5. Expresa en forma de potencias:
1. 50 000=
2. 3 200=
3. 3 000 000=
6.Escribe en forma de una sola potencia:
1. 33 · 34 · 3 =
2. 57 : 53 =
3. (53)4 =
4. (5 · 2 · 3)4 =
5. (34)4 =
6. [(53)4 ]2 =
7. (82)3
8. (93)2
9. 25 · 24 · 2 =
10. 27: 26 =
11. (22)4 =
12. (4 · 2 · 3)4 =
13. (25)4 =
14. [(23)4]0=
15. (272)5=
16. (43)2 =
7. Utilizando potencias, haz la descomposición polinómica
de estos números:
1. 3 257
2. 10 256
3. 125 368
8.Calcular las raíces:
1.
2.
3.
9.Realiza las siguientes operacione s combinadas teniendo en
cuenta su prioridad:
1. 27 + 3 · 5 – 16 =
2. 27 + 3 – 45: 5 + 16 =
3. (2 · 4 + 12) (6 − 4) =
4. 3 · 9 + (6 + 5 – 3) – 12: 4 =
5. 2 + 5 · (2 · 3)³ =
6. 440 − [30 + 6 (19 − 12)] =
7. 2{4 [7 + 4 (5 · 3 − 9)] − 3 (40 − 8)} =
8. 7 · 3 + [6 + 2 · (23: 4 + 3 · 2) – 7 ·
] + 9 : 3 =
Pr o b l e m as d e núm e r o s na t ur a le s
1 Dados los números 5, 7 y 9 forma todos los números posibles
de tres cifras distintas, ordénalos de menor a mayor y súm alos.
2 El cociente de una división exacta es 504, y el divisor 605.
¿Cuál es el dividendo?
3 El cociente de una división entera es 21, el divisor 15 y el
dividendo 321. ¿Cuál es el resto?
4 Pedro compró una finca por 643 750 € y la vendió ganando
75 250 €. ¿Por cuánto lo vendió?
5 Con el dinero que tengo y 247 € más, podría pagar una
deuda de 525 € y me sobrarían 37 €. ¿Cuánto dinero tengo?
6 Se compran 1600 Kg de boquerones, a razón de 4 €/K g. Si
los portes cuestan 400 € y se desea ganar con la venta 1200€. ¿A
cuánto debe venderse el kilogramo de boquerones?
7 ¿Cuántos años son 6 205 días? Consideramos que un año
tiene 365 días.
8 Pedro quiere comprar un automóvil. En la tienda le ofrecen
dos modelos: uno de dos puertas y otro de cuatro puertas. En ambos
modelos los colores disponibles son: blanco, azul, rojo, gris y verde.
Halla el número de posibles elecciones que tiene Pedro.
9 En una piscina caben 45 000 litros. ¿Cuánto tiempo tarda en
llenarse mediante un grifo que echa 15 litros por minuto?
10
En
un
aeropuerto
aterriza
un
avión
cada
10
minutos.
¿Cuántos aviones aterrizan en un día?
11 En una urbanización viven 4 500 personas y hay un árbol
por cada 90 habitantes. ¿Cuántos árboles hay en l a urbanización?
¿Cuántos árboles habrá que plantar para tener un árbol por cada 12
personas?
E j er ci ci o s y p r ob l e m a s d e d i vi si b i l i d a d
1
Calcular todos los múltiplos de 17 comprendidos entre 800 y
860.
2
De
los
siguientes
números:
179,
311,
848,
3566,
7287.
Indicar cuáles son primos y cuáles compuestos.
3
Calcular,
mediante
una
tabla,
todos
los
números
comprendidos entre 400 y 450.
4
Descomponer en factores primos:
1. 216
2. 360
3. 432
5
Factorizar 342 y calcular su número de divisores.
6
Descomponer en factores
1.
2250
2. 3500
3. 2520
primos
7
Calcular el m. c. d. y m.c.m. de:
1. 428 y 376
2. 148 y 156
3. 600 y 1 000
8Calcular
el m. c. d. y m.c.m. de:
1. 72, 108 y 60
2. 1048, 786 y 3930
3. 3120, 6200 y 1864
9
Calcular el m.c.d. de:
1. 72 y 16
2. 656 y 848
3. 1278 y 842
Pr o b l e m as d e divi s i b i l i d a d
1
Un
faro
se
enciende
cada
12
segundos,
otro
cada
18
segundos y un tercero cada minuto. A las 6.30 de la tarde los tres
coinciden.
Averigua
las
veces
que
volverán
a
coincidir
en
los
cinco
minutos siguientes.
2
Un viajero va a Barcelona cad a 18 días y otro cada 24 días.
Hoy han estado los dos en Barcelona.
¿Dentro de cuantos días volverán a estar los dos a la vez en
Barcelona?
3
¿Cuál es el menor número que al dividirlo separadamente
por 15, 20, 36 y 48, en cada caso, da de resto 9?
4
En una bodega hay 3 toneles de vino, cuyas capacidades
son: 250 l, 360 l, y 540 l. Su contenido se quiere envasar en cierto
número de garrafas iguales. Calcular las capacidades máximas de
estas
garrafas
para
que
en
ellas
se
pueden
envasar
el
vino
contenido en cada uno de los toneles, y el número de garrafas que
se necesitan.
5
El suelo de una habitación, que se quiere embaldosar, tiene
5 m de largo y 3 m de ancho.
Calcula el lado y el número de la baldosas, tal que el número
de baldosas que se coloque sea mínim o y que no sea necesario
cortar ninguna de ellas.
6
Un comerciante desea poner en cajas 12 028 manzanas y 12
772 naranjas, de modo que cada caja contenga el mismo número de
manzanas o de naranjas y, además, el mayor número posible. Hallar
el número de naranjas de cada caja y el número de cajas necesarias.
7
¿Cuánto mide la mayor baldosa cuadrada que cabe en un
número exacto de veces en una sala de 8 m de longitud y 6.4 m de
anchura? ¿Y cuántas baldosas se necesitan?
E j er ci ci o s y p r ob l e m a s d e númer o s e nte r o s
1Ordenar,
en sentido creciente, representar gráficamente, y
calcular los opuestos y valores absolutos de los siguientes números
enteros:
8, −6, −5, 3, −2, 4, −4, 0, 7
2
Representar gráficamente, y calcular los opuestos y valores
absolutos de los siguientes números enteros:
−4, 6, −2, 1, −5, 0, 9
3
Sacar factor común en las expresiones:
1 3 · 2 + 3 · (−5) =
2(−2) · 12 + (−2) · (−6) =
38 · 5 + 8 = 8 · (5 + 1) =
4 (−3) · (−2) + (−3) · (−5) =
4
Realizar las siguientes operaciones con números enteros
1 (3 − 8) + [5 − (−2)] =
2 5 − [6 − 2 − (1 − 8) − 3 + 6] + 5 =
3 9: [6: (− 2)] =
4 [(−2)5 − (−3)3]2 =
5 (5 + 3 · 2: 6 − 4) · (4: 2 − 3 + 6): (7 − 8: 2 − 2) 2 =
6 [(17 − 15)3 + (7 − 12)2] : [(6 − 7) · (12 − 23)] =
5
Realizar las siguientes operaciones con números enteros
1 (7 − 2 + 4) − (2 − 5) =
2 1 − (5 − 3 + 2) − [5 − (6 − 3 + 1) − 2]=
3 −12 · 3 + 18: (−12: 6 + 8) =
6
1
2
Calcula, si existe:
3
4
5
6
7Realizar
las
siguientes
operaciones
con
potencias
de
potencias
de
números enteros:
1 (−2)2 · (−2)3 · (−2)4 =
2 (−8) · (−2)2 · (−2)0 (−2) =
3 (−2)2 · (−2)3 · (−2)4 =
4 22 · 23 · 24 =
5 210 : 23 =
6 29 : 23 =
7 26 : 23 =
8 25 : 23 =
9 [(−2)2]
3
· (−2)3 · (−2)4 =
10 [(−2)6: (−2)3]3 · (−2) · (−2)4 =
8
Realizar
las
números enteros:
siguientes
operaciones
con
1 (−3)1 · (−3)3 · (−3)4 =
2 (−27) · (−3) · (−3)2 · (−3)0=
3 (−3)2 · (−3)3 · (−3)4 =
4 32 · 34 · 34 =
5 55: 53 =
6 56: 53 =
7 54: 5
3
=
8 51: 53 =
9 (−3)1 · [(−3)3]2 · (−3)4 =
10 [(−3)6 : (−3)3]
3
· (−3)0 · (−3)4 =
Pr o b l e m as d e núm e r o s e nt er o s
1Un
emperador romano nació en el año 63 a. C . y murió en el
14 d. C. ¿Cuántos años vivió?
2Una
bomba
extrae
el
petróleo
de
un
pozo
a
975
m
de
profundidad y lo eleva a un depósito situado a 48 m de altura. ¿Qué
nivel supera el petróleo?
3¿Qué
diferencia de temperatura soporta una persona que pasa
de la cámara de conservación de las verduras, que se encuentra a 4
ºC, a la del pescado congelado, que está a −18 ºC? ¿Y si pasara de
la cámara del pescado a la de la verdura?
4
La
temperatura
del
aire
baja
según
se
asciende
en
la
atmósfera, a razón de 9 ºC c ada 300 metros. Si la temperatura al
nivel del mar en un punto determinado es de 0ªC, ¿a qué altura
vuela un avión si la temperatura del aire es de −81 ºC?
5
En un depósito hay 800 l de agua. Por la parte superior un
tubo vierte en el depósito 25 l por min uto, y por la parte inferior
por otro tubo salen 30 l por minuto. ¿Cuántos litros de agua habrá
en el depósito después de 15 minutos de funcionamiento?
E j er ci ci o s d e nú m e ro s d e cim a l es
1
Ordena de menor a mayor estos números decimales:
5.4,
5.004,
5.0004,
5.04,
4.4,
4.98,
5,
5.024
7.3,
7.003,
7.0003,
7.03,
6.5,
6.87,
7,
7.037
Clasificar,
por
2
el
tipo,
los
números
decimales
correspondientes a las fracciones:
3
Realizar las siguientes operaciones con números decimales:
3.6669 · 1000 =
3.6669 : 1000 =
0.036 · 10 =
0.036 : 10 =
0.000012 · 10 000 =
123.005 : 10 000 =
26.36 · 10 000 =
2.36 : 1000 =
0.261 · 100 =
5.036 : 10 =
4
Resuelve las siguientes divisiones de números decimales :
324 : 0.018
12.96 : 6
5
Calcula la raíz cuadrada:
Pr o b l e m as d e núm e r o s d e ci m ale s
1
Una jarra vacía pesa 0.64 kg, y llena de agua 1.728 kg.
¿Cuánto pesa el agua?
2
Un ciclista ha recorrido 145.8 km en una etapa, 136.65 km
en otra etapa y 162.62 km en una tercera etapa.
¿Cuántos kilómetros le quedan por recorrer si la carrera es de
1000 km?
3
De un depósito con agua s e sacan 184.5 l y después 128.75
l, finalmente se sacan 84.5 l. Al final quedan en el depósito 160 l.
¿Qué cantidad de agua había el depósito?
4
Se tienen 240 cajas con 25 bolsas de café cada una. Si cada
bolsa pesa 0.62 kg, ¿cuál es el peso del café?
5
Sabiendo que 2.077 m³ de aire pesan 2.7 kg, calcular lo que
pesa 1 m³ de aire.
6
Eva sigue un régimen de adelgazamiento y no puede pasar
en cada comida de 600 calorías.
Ayer almorzó: 125 g de pan, 140 g de espárragos, 45 g de
queso y una manzana de 130 g.
Si 1 g de pan da 3.3 calorías, 1 g de espárragos 0.32, 1 g de
queso 1.2 y 1 g de manzana 0.52.
¿Respetó Eva su régimen?
E j er ci ci o s y p r ob l e m a s d e f r a cci o ne s
1
Asociar
cada
fracción
de
hora
con
los
minutos
correspondientes:
2
Halla los pares de fracciones equivalentes y colócalas en
parejas:
3
Escribe los inversos de:
4
Escribe el signo > o <, donde corresponda.
5
Compara las siguientes fracciones:
6
Ordenar de menor o mayor:
7
Clasifica las siguientes fracciones en propias o impropias:
8
Opera:
9
Realiza de dos modos distintos:
10
Resuelve:
11
Resuelve:
12
Efectúa las divisiones
Pr o b l e m as d e f ra cci o ne s
1
Calcula qué fracción de la unidad representa:
1 La mitad de la mitad.
2 La mitad de la tercera parte.
3 La tercera parte de la mitad.
4 La mitad de la cuarta parte.
2
Para preparar un pastel, se necesita:
1/3 de un paquete de 750 g de azúcar.
3/4 de un paquete de harina de kilo.
3/5 de una barra de mantequilla de 200 g.
Halla,
en
gramos,
las
cantidades
que
se
necesitan
para
preparar el pastel.
3
Un depósito contiene 150 l de agua. Se consumen los 2/5 de
su contenido. ¿Cuántos litros de agua quedan?
4
De
una
pieza
de
tela
de
48
m
se
cortan
3/4.
¿Cuántos
metros mide el trozo restante?
5
Una familia ha consumido en un día de ver ano:
Dos botellas de litro y medio de agua.
4 botes de 1/3 de litro de zumo.
5 limonadas de 1/4 de litro.
¿Cuántos litros de líquido han bebido? Expresa el resultado con
un número mixto.
6
¿Cuantos tercios de litro hay en 4 l?
7
Un cable de 72 m de longi tud se corta en dos trozos. Uno
tiene las 5/6 partes del cable. ¿Cuántos metros mide cada trozo?
8
Una caja contiene 60 bombones. Eva se comió 1/5 de los
bombones y Ana 1/2.
¿Cuántos bombones se comieron Eva, y Ana?
¿Qué fracción de bombones se comieron entre las dos?
9
Ana ha recorrido 600 m, que son los 3/4 del camino de su
casa al instituto. ¿Qué distancia hay de su casa al instituto?
10
Dos automóviles A y B hacen un mismo trayecto de 572
km. El automóvil A lleva recorrido los 5/11 del trayecto cuando el B
ha
recorrido
los
6/13
del
mismo.
¿Cuál
de
los
dos
va
primero?
¿Cuántos kilómetros llevan recorridos cada uno?
11
En las elecciones locales celebradas en un pueblo, 3/11 de
los votos fueron para el partido A, 3/10 para el partido B, 5/14 para
C y el resto para el partido D. El total de votos ha sido de 15.400.
Calcular:
1 El número de votos obtenidos por cada partido.
2 El número de abstenciones sabiendo que el número de
votantes representa 5/8 del censo electoral.
12
Elena va de
compras con 180
€. Se
gasta 3/5
de
esa
cantidad. ¿Cuánto le queda?
13
Hace unos años Pedro tenía 24 años, que representan los
2/3 de su edad actual. ¿Qué edad tiene Pedro?
14
Un padre reparte entre sus hijos 1800 €. Al mayor le da
4/9 de esa cantidad, al mediano 1/3 y al menor
cantidad
recibió
cada
uno?
¿Qué
fracción
del
el resto. ¿Qué
dinero
recibió
el
tercero?
15
emplean
Los 2/5 de los ingresos de una comunidad de vecinos se
combustible,
1/8
se
emplea en electricidad, 1/12 en
la
recogida de basuras, 1/4 en mantenimiento del ed ificio y el resto se
emplea en limpieza.
1 ¿Qué fracción de los ingresos se emplea en limpieza?
2 De acuerdo con la fracción de ingresos empleada, ordena las
partidas enumeradas de menor a mayor.
16
Alicia dispone de 300 € para compras. El jueves gastó 2/5
de esa cantidad y el sábado los 3/4 de lo que le quedaba. ¿Cuánto
gastó cada día y cuánto le queda al final?
E j er ci ci o s y p r ob l e m a s d e p ro po r ci o na l i d a d
1
Calcular
el
término
desconocido
de
las
sig uientes
proporciones:
1
2
3
4
5
2
Dos ruedas están unidas por una correa transmisora. La
primera tiene un radio de 25 cm y la segunda de 75 cm. Cuando la
primera
ha
dado
300
vueltas,
¿cuántas
vueltas
habrá
dado
la
segunda?
3
Seis personas pueden vivir en un hotel durante 12 días por
792 €. ¿Cuánto costará el hotel de 15 personas durante ocho días?
4
Con 12 botes conteniendo cada uno ½ kg de pintura se han
pintado 90 m de verja de 80 cm de altura. Calcular cuántos botes de
2 kg de pintura serán necesari os para pintar una verja similar de
120 cm de altura y 200 metros de longitud.
5
48
de
11 obreros labran un campo rectangular de 220 m de largo y
ancho
en 6 días. ¿Cuántos obreros serán necesarios para
labrar otro campo análogo de 300 m de largo por 56 m d e ancho en
cinco días?
6
de
Seis grifos, tardan 10 horas en llenar un depósito de 400 m³
capacidad. ¿Cuántas horas tardarán cuatro
grifos en llenar 2
depósitos de 500 m³ cada uno?
7
De los 800 alumnos de un colegio, han ido de viaje 600.
¿Qué porcentaje d e alumnos ha ido de viaje?
8
Una
moto
cuyo
precio
era
de
5.000
€,
cuesta
en
la
actualidad 250 € más. ¿Cuál es el porcentaje de aumento?
9
Al adquirir un vehículo cuyo precio es de 8800 €, nos hacen
un descuento del 7.5%. ¿Cuánto hay que pagar por el vehí culo?
10
Al comprar un monitor que cuesta 450 € nos hacen un
descuento del 8%. ¿Cuánto tenemos que pagar?
11
Se vende un artículo con una ganancia del 15% sobre el
precio de costo. Si se ha comprado en 80 €. Halla el precio de
venta.
12
Cuál será el precio que hemos de marcar en un artículo
cuya compra ha ascendido a 180 € para ganar al venderlo el 10%.
13
¿Qué
precio
de
venta
hemos
de
poner
a
un
artículo
comparado a 280 €, para perder el 12% sobre el precio de venta?
14
Se vende un objeto perdiendo el 20% sobre el precio de
compra. Hallar el precio de venta del citado artículo cuyo valor de
compra fue de 150 €.
E j er ci ci o s y p r ob l e m a s d e p ro po r ci o na l i d a d
1
Un abuelo reparte 450 € entre sus tres nietos de 8, 12 y 16
años de edad; proporcionalmente a sus edade s. ¿Cuánto corresponde
a cada uno?
2
Se asocian tres individuos aportando 5000, 7500 y 9000 €.
Al cabo de un año han ganado 6 450 €. ¿Qué cantidad corresponde a
cada
uno
si
hacen
un
reparto
directamente
proporcional
a
los
capitales aportados?
3
Se
reparte
una
cantidad
de
dinero, entre
tres
personas,
directamente proporcional a 3, 5 y 7. Sabiendo que a la segunda le
corresponde 735 €. Hallar lo que le corresponde a la primera y
tercera.
4
Se reparte dinero en proporción a 5, 10 y 13; al menor le
corresponden 2500 €. ¿Cuánto corresponde a los otros dos?
5
Tres hermanos ayudan al mantenimiento familiar entregando
anualmente 5900 €. Si sus edades son de 20, 24 y 32 años y las
aportaciones son inversamente proporcionales a la edad, ¿cuánto
aporta cada uno?
6
Repartir 420 €, entre
tres niños en partes inversamente
proporcionales a sus edades, que son 3, 5 y 6.
7
¿Durante cuánto tiempo ha de imponerse un capital de 25
000 € al 5% para que se convierta en 30.000 €?
8
Se prestan 45 000 € y al cabo de un año, 4 meses y 20 días
se reciben 52 500 €. Calcular el tanto por ciento de interés.
9
Hallar él tanto por ciento de interés simple al que deberá
prestarse un capital para que al cabo de 20 años los intereses sean
equivalentes al capital prestado.
10
¿En cuánto tiempo se triplica un capital colocado al 6%?
E j er ci ci o s d el s is t e m a mé t ri co de ci m a l
1
Expresa en metros:
1. 3 km 5 hm 7 dam
2. 7 m 4 cm 3 mm
3. 25.56 dam + 526.9 dm
4. 53 600 mm + 9 830 cm
5. 1.83 hm + 9.7 dam + 3 700 cm
2
Expresa en litros:
1. 3 kl 5 hl 7 dal
2. 7 l 4 cl 3 ml
3. 25.56 dal + 526.9 dl
4. 53 600 ml + 9 830 cl
5. 1.83 hl + 9.7 dal + 3 700 cl
3Expresa
en gramos:
1. 5 kg 3 hg 4 g
2. 4 hg 8 dag 2 g 5 dg
3. 2 dag 3 g 8 dg 7 cg
4. 35 dg 480 cg 2 600 mg
4Expresa
en centilitros:
1. 3 dal 7l 5 dl 4 cl 5 ml
2. 6 hl 8 l 2 ml
3. 0.072 kl + 5.06 dal + 400 ml
4. 0.000534 kl + 0.47 l
5
Expresa en centígramos:
1. 3 dag 7 g 5 dg 4 cg 5 mg
2. 6 hg 8 g 2 mg
3. 0.072 kg + 5.06 dag + 400 mg
4. 0.000534 kg + 0.47 g
6
Expresa en metros:
1. 5 km 3 hm 4 m
2. 4 hm 8 dam 2 m 5 dm
3. 2 dam 3 m 8 dm 7 c m
4. 35 dm 480 cm 2 600 mm
E j er ci ci o s d el S is t e m a M ét r i co D e ci m a l
1
Pasa a decímetros cuadrados:
1. 0.027 dam2
2. 0.35 m2
3. 438 cm2
4. 90 000 mm2
2
Expresa en metros cuadrados:
1. 5 hm2 24 dam2 60 dm2 72 cm2
2. 0.00351 km2 + 4700 cm2
3. 0.058 hm2 − 3.321 m2
3
Expresa en hectáreas:
1. 431 943 a
2. 586 500 m2
3. 0.325 km2
4. 7 km2 31 hm2 50 dam2
5. 51 m2 33 dm2 70 cm2
4
Calcula y expresa el resultado en forma compleja:
1. 0.03598 km2 + 96.45 ha + 3 000 a
2. 179.72 m2 − 0.831 dam2
3. 52 dam2 31 m2 500 cm2
5
Pasa a centímetros cúbicos:
1. 5.22 dm3
2. 6 500 mm3
3. 3.7 dl
4. 25 cl
6
Expresa en litros:
1. 13.2 m3
2. 0.05 m3
3. 3.9 dm3
4. 7 700 cm3
13
Calcula y expresa el resultado en metros cúbicos:
1. 7 200 dm3 + (3.5 m3 4 600 dm3)
2. 0.015 hm3 − (570 m3 5.3 dm3)
R e s o l ve r l a s e cua ci o ne s d e p r im e r g r a d o
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Pr o b l e m as d e ecua ci o ne s d e p ri m er g r a d o
1
Un padre tiene 35 años y su hijo 5. ¿Al cabo de cuántos años
será la edad del padre tres veces mayor que la edad del hijo?
2
Si al doble de un número se le resta su mitad resulta 54.
¿Cuál es el número?
3
La base de un rectángulo es doble que su altura. ¿Cuáles son
sus dimensiones si el perímetro mide 30 cm?
4
En
una
reunión
hay
doble
número
de
mujeres
que
de
hombres y triple número de niños que de hombres y mujeres juntos.
¿Cuántos hombres, mujeres y niños hay si la reunión la componen
96 personas?
5
l
y
el
Se han consumido 7/8 de un bidón de aceite. Reponemos 38
bidón
ha
quedado
lleno
hasta
sus
3/5
partes .
Calcula
la
capacidad del bidón.
6
Una granja tiene cerdos y pavos, en total hay 35 cabezas y
116 patas. ¿Cuántos cerdos y pavos hay?
7
Luís hizo un viaje en el coche, en el cual consumió 20 l de
gasolina. El trayecto lo hizo en dos etapas: en la primera, consumió
2/3 de la gasolina que tenía el depósito y en la segunda etapa, la
mitad de la gasolina que le queda. Se pide:
1. Litros de gasolina que tenía en el depósito.
2. Litros consumidos en cada etapa.
8
su
En una librería, Ana compra un libro con la terce ra parte de
dinero
y
un
cómic
con
l as dos terceras
partes de
lo
que
le
quedaba. Al salir de la librería tenía 12 €. ¿Cuánto dinero tenía
Ana?
9
La dos cifras de un número son consecutivas. La mayor es la
de las decenas y la menor la de las unidades. El número es igual a
seis veces la suma d e las cifras. ¿Cuál es el número?
10
Las
tres
cuartas
partes
de
la
edad
del
padre
de
Juan
excede en 15 años a la edad de éste. Hace cuatro años la edad de la
padre era doble de la edad del hijo. Hallar las edades de ambos.
11
Trabajando juntos, dos obreros tardan en hacer un trabajo
14 horas. ¿Cuánto tiempo tardarán en hacerlo por separado si uno
es el doble de rápido que el otro?
12
Halla el valor de los tres ángulos de un triángulo sabiendo
que B mide 40° más que C y que A mide 40° más que B.
Pr o b l e m as d e re l o je s , m ó vi le s , g r i fo s y me zcl a s
1
Un reloj marca las 3 en punto. ¿A qué hora entre las 3 y las
4 se superpondrán las agujas?
2
Un reloj marca las 2 en punto. ¿A qué hora formarán sus
agujas por primera vez un ángulo recto?
3
Dos ciudades A y B distan 3 00 km entre sí. A las 9 de la
mañana parte de la ciudad A un coche hacia la ciudad B con una
velocidad de 90 km/h, y de la ciudad B parte otro hacia la ciudad A
con una velocidad de 60 km/h. Se pide:
1 El tiempo que tardarán en encontrarse.
2 La hora del encuentro.
3 La distancia recorrida por cada uno.
4
Dos ciudades A y B distan 180 km entre sí. A las 9 de la
mañana sale de un coche de cada ciudad y los dos coches van en el
mismo sentido. El que sale de A circula a 90 km/h, y el que sale de
B va a 60 km/h. Se pide:
1 El tiempo que tardarán en encontrarse.
2 La hora del encuentro.
3 La distancia recorrida por cada uno.
5
Un coche sale de la ciudad A a la velocidad de 90 km/h. Tres
horas más tarde sale de la misma ciudad otro coche en persecución
del primero con una velocidad de 120 km/h. Se pide:
1 El tiempo que tardará en alcanzarlo.
2 La distancia a la que se produce el encuentro.
6
Un camión sale de una ciudad a una velocidad de 40 km/h.
Una hora más tarde sale de la misma ciudad y en la misma dirección
y sentido un coche a 60 km/h. Se pide:
1. Tiempo que tardará en alcanzarle.
2. Distancia al punto de encuentro.
7
Dos ciclistas salen en sentido contrario a las 9 de la mañana
de los pueblos A y B situados a 130 kilómetros de distancia. El
ciclista que sale de A pedalea a una velocidad constante de 30 km/h,
y el ciclista que sale de B, a 20 km/h. ¿A qué distancia de A se
encontrarán y a qué hora?
8Un
grifo tarda en llenar un depósito tres horas y otro grifo
tarda en llenarlo cuatro horas. ¿Cuánto tiempo tard arán en llenar
los dos grifos juntos el depósito?
9
Un comerciante tiene dos clases de café, la primera a 40 € el
kg y la segunda a 60 € el kg.
¿Cuantos kilogramos hay que poner de cada clase de café para
obtener 60 kilos de mezcla a 50 € el kg?
10
Se tienen dos lingotes de plata, uno de ley 0.750 y otro de
ley 0.950. ¿Qué peso hay que tomar de cada lingote para obtener
1800 g de plata de ley 0.900?
11
Un lingote de oro de ley 0.950 pesa 6 300 g. ¿Qué cantidad
de cobre puro se habrá de añadir para rebajar su ley a 0.900?
Puntos
Un punto no tiene dimensiones.
Sirve para indicar una posición.
Se nombran con letras mayúsculas.
Rectas
Una recta tiene una dimensión: longitud.
Se
designan
mediante
dos
de
sus
puntos
o
mediante
minúscula.
Dos puntos determinan una recta .
Dos rectas que se cortan determinan u n punto.
una
letra
Una recta indica una dirección y dos sentidos contrarios , según se
recorra la recta de izquierda a derecha o de derecha izquierda.
Semirrectas
Una semirrecta es cada una de las partes en que queda dividida
una recta por uno cualquiera de sus puntos.
Pl a no s
Un plano posee dos dimensiones: longitud y anchura.
Se nombran mediante letras griegas: α (alfa), β (beta)...
Dos planos que se cortan determinan una recta.
Un plano viene determinado por:
Tres puntos no alineados.
Dos rectas que se cortan.
Dos rectas paralelas.
Por un punto y una recta.
Semiplanos
Un semiplano es cada una de las partes en que queda dividido un
plano por una cualquiera de sus rectas.
Posiciones relativas de rectas en un plano
Rectas paralelas
Son las que estando en el mismo plano, no son secantes.
Rectas secantes
Son
las
que
se
cortan
en
un
único
punto,
llamado
punto
de
intersección.
Rectas coincidentes
Son aquellas en las que todos sus puntos se superponen.
Rectas perpendiculares
Son dos rectas secantes que dividen un plano en cuatro partes
iguales.
S e g m e nt os
Definición de segmento
Segmento es la porción de recta limitada por dos puntos,
llamados extremos.
Se designa por los puntos que lo limitan o por una letra
minúscula.
Tipos de segmentos
Segmento nulo
Un segmento es nulo cuando sus extremos coinciden.
Segmentos consecutivos
Dos segmentos son consecutivos cuando tienen un extremo en
común.
Segmentos alineados o adyacentes
Dos segmentos consecutivos están alineados cuando pertenecen
a la misma recta.
Mediatriz de un segmento
La mediatriz de un segmento es la recta que pasa por el punto
medio del segmento y es perpendicular a él.
O p e r a ci o ne s con s e g m e nto s
Suma de segmentos
La suma de dos segmentos es otro segmento que tiene por inicio
el origen del primer segmento y como final el final del segundo
segmento.
La longitud del segmento suma es igual a la suma de las longitudes
de los dos segmentos que lo forman.
Resta de segmentos
La resta de dos segmentos es otro segmento que tiene por origen el
final del segmento menor y por final el final del segmento mayor.
La
longitud
del
segmento
diferencia
es
igual
a
la
resta
de
las
longitudes de los dos segmentos.
Producto de un número por un segmento
El producto de un número con un segmento es ot ro segmento resultado
de repetir el segmento tantas veces como indica el número por el que
se multiplica.
La longitud del segmento obtenido es igual al número por la longitud
del segmento inicial.
División de un segmento por un número
La división de un segmento por un número es otro segmento tal
que
multiplicado
original.
por
ese
número
da
como
resultado
el
segmento
La longitud del segmento obtenido es igual la longitud del segmento
inicial divido por el número.
División de un segmento en partes
Dividir el segmento AB en 3 partes iguales.
1. Se dibuja una semirrecta de origen el extremo A del segmento.
2.
Tomando
como
unidad
cualquier
medida,
se
señalan
en
la
semirrecta 3 unidades de medida a partir de A.
3. Por cada una de las divisiones de la semirre cta se trazan rectas
paralelas al segmento que une B con la última división sobre la
semirrecta. Los puntos obtenidos en el segmento AB determinan las
3 partes iguales en que se divide.
S u ma d e án g ul os
Gráfica
La suma de dos ángulos es otro ángulo cuya amplitud es la suma
de las amplitudes de los dos ángulos iniciales.
Numérica
1º Para sumar ángulos se colocan los grados debajo de los
grados, los minutos debajo de los minutos y los segundos debajo
de los segundos; y se suman.
2º Si los segundos suman más de 60, se divide dicho
número entre 60; el resto serán los segundos y el cociente se
añadirán a los minutos.
3º Se hace lo mismo para los minutos.
R e s t a d e á ng ul os
Gráfica
La
resta
de
dos
ángulos
es
otro
ángulo
cuya
amplitud
es
la
diferencia entre la amplitud del ángulo mayor y la del ángulo
menor.
Numérica
1º Para restar ángulos se colocan los grados debajo de los
grados, los minutos debajo de los minutos y los segundos debajo
de los segundos.
2º Se restan los segundos. Caso de que no sea pos ible,
convertimos
un
minuto
del
minuendo
en
60
segundos
y
se
lo
sumamos a los segundos del minuendo. A continuación restamos los
segundos.
3º Hacemos lo mismo con los minutos.
M ul t i p l i ca ci ó n de á ng ul o s
Gráfica
La multiplicación de un número por un ángulo es otro ángulo cuya
amplitud
es
la
suma
de
tantos
ángulos
iguales
al
dado
como
indique el número.
Numérica
1º
número.
Multiplicamos
los
segundos,
minutos
y
grados
por
el
2º Si los segundos sobrepasan los 60, se divide dicho número
entre 60; el resto serán los segundos y el cociente se añadirán a los
minutos.
3º Se hace lo mismo para los minutos.
D i vi s i ó n de á ng ul o s
Gráfica
La división de un ángulo por un número es hallar otro ángulo tal
que multiplicado por ese número da como resultado el ángulo original.
:4 =
Numérica
Dividir 37º 48' 25'' entre 5
1º Se dividen los grados entre el número.
2º El cociente son los grados y el resto, multiplicando por 60,
los minutos.
3º Se añaden estos minutos a los que tenemos y se repite el
mismo proceso con los minutos.
4º Se añaden estos segundos a los que tenemos y se dividen
los segundos.
Clasificación de ángulos según su medida
Agudo < 90°
Recto = 90°
Obtuso>90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Nulo = 0º
Completo = 360°
Negativo < 0º
Mayor de 360°
Tipos de ángulos según su posición
Ángulos consecutivos
Ángulos consecutivos son aquellos que tienen el vértice y un lado
común.
Ángulos adyacentes
Ángulos adyacentes son aquellos que tienen el vértice y un
lado común, y los otros lados situados uno en polongación del
otro.
Forman un ángulo llano.
Ángulos opuestos por el vértice
Son
los
que
teniendo
el
vértice
prolongación de los lados del otro.
Los ángulos 1 y 3 son iguales.
Los ángulos 2 y 4 son iguales.
común,
los
lados
de
uno
son
Clases de ángulos según su suma
Ángulos complementarios
Dos ángulos son complementarios si suman 90°.
Ángulos suplementarios
Dos ángulos son suplementarios si suman 180°.
Ángulos entre paralelas y una recta transversal
Ángulos correspondientes
Los ángulos 1 y 2 son iguales.
Ángulos alternos internos
Los ángulos 2 y 3 son iguales.
Ángulos alternos externos
Los ángulos 1 y 4 son iguales.
Á ng ul o s e n l a ci r cunf e r e nci a
Ángulo central
El ángulo central tiene su vértice en el centro de la circunferencia
y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
Ángulo inscrito
El ángulo inscrito tiene su vértice está en la circunferencia y sus
lados son secantes a ella.
Mide la mitad del arco que abarca.
Ángulo semiinscrito
El vértice de ángulo semiinscrito está en la circunferencia, un
lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
Ángulo interior
Su vértice es interior a la circunferencia y sus lados
secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan
sus lados y las prolongaciones de sus lados.
Ángulo exterior
Su vértice es un punto exterior a la circunferencia y los lados de
sus
ángulos
son:
o
secantes
a
ella,
o
uno
tangente
y
otro
secante, o tangentes a ella:
Mide la mitad de la diferencia entre las medidas de los arcos que
abarcan sus lados sobre la circunferencia.
Á n g ul os d e un p ol íg on o r e gu la r
Ángulo central de un polígono regular
Es el formado por dos radios consecutivos.
Si n es el número de lados de un polígono:
Ángulo central = 360° : n
Ángulo central del pentágono regular= 360° : 5 = 72º
Ángulo interior de un polígono regular
Es el formado por dos lados consecutivos.
Ángulo interior =180° − Ángulo central
Ángulo interior del pentágono regular = 180° − 72º = 108º
Ángulo exterior de un polígono regular
Es
el
formado
por
un
lado
y
la
prolongación
de
un
lado
consecutivo.
Los ángulos exteriores e interiores son suplementarios , es decir,
que suman 180º.
Ángulo exterior = Ángulo central
Ángulo exterior del pentágono regular = 72º
Definición de bisectriz
La bisectriz de un ángulo es la recta que pasando por el vértice del
ángulo lo divide en dos ángulos iguales.
Trazar la bisectriz
1º Se traza un arco correspondiente al ángulo
2º Desde los dos extremos del arco trazado se trazan, con
cualquier abertura del compás, dos arcos que han de cortarse en un
punto.
3º La bisectriz se obtiene dibujando la recta que une ese
punto con el vértice.
Otra forma de dibujar la bisectriz de un ángulo
1.Con
centro
en
el
vértice
del
ángulo
se
traza
una
circunferencia de cualquier amplitud.
2.Desde los puntos de corte de la circunferencia con los lados
del ángulo se trazan dos circunferencias con el mismo radio.
3.La recta que pasa por el vértice del ángulo y uno de los
puntos de corte de las circunferencias es la bisectriz.
I n c en t r o
El
incentro
es
el
punto
es
el
centro
de
corte
de
las
tres
bisetrices
de
un
triángulo.
El
incentro
triángulo.
de
una
circunferencia
inscrita
en
el
A p l i ca ci o ne s del t e or em a d e Pitá g o r a s . E je r ci cio s
1
La hipotenusa de un triángulo rectángulo mide 405.6 m y la
proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.
2
Calcular los lados de un triángulo rectángulo sabiendo que la
proyección de uno de los catetos sobre la hipotenusa es 6 cm y la
altura relativa de la misma
3
cm.
Una escalera de 10 m de longitud está apoyada sobre la
pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura
alcanza la escalera sobre la pared?
4
Determinar el lado de un triángulo equilátero cuyo perímetro
es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus
áreas?
5
Calcular el área de un triángulo equilátero inscrito en una
circunferencia de radio 6 cm.
6
Determinar
el
área
del
cuadrado
inscrito
en
una
circunferencia de longitud 18.84 cm.
7
este
En un cuadrado de 2 m de lado se inscribe un círculo y en
círculo
un
cuadrado
y
en
este
otro
círculo.
Hallar
el
área
comprendida entre el último cuadrado y el último círculo.
8
bases
El perímetro de un trapecio isósceles es de 110 m, las
miden
40
y
paralelos y el área.
30
m
respectivamente.
Calcular
los
lados
no
9
A un hexágono regular 4 cm de lado se le inscribe una
circunferencia y se le circunscribe otra. Hallar el área de la corona
circular así formada.
10
En una circunferencia una cuerda mide 48 cm y dista 7 cm
del centro. Calcular el área del círculo.
11
Los catetos de un triángulo inscrito en una circunferencia
miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la
circunferencia y el área del círculo.
12Sobre
un círculo de 4 cm de radio se traza un ángulo central de 60°.
Hallar el área del segmento circular comprendido entre la cuerda que une
los extremos de los dos radios y su arco correspondiente.
Te o r em a d e Pitá g o r a s
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual
a la suma de los cuadrados de los catetos.
Aplicaciones del teorema de Pitágoras
1 Conociendo los dos catetos ca lcular la hipotenusa
Los
catetos
de
un
triángulo
rectángulo
miden
respectivamente. ¿Cuánto mide la hipotenusa?
en
3
m
y
4
m
2 Conociendo la hipotenusa y un cateto, calcular el otro cateto
La
hipotenusa
de
un
triángulo
rectángulo
mide
5
m
y
uno
de
s us
catetos 3 m. ¿Cuánto mide otro cateto?
3 Conociendo sus lados, averiguar si es rectángulo
Para que sea rectángulo el cuadrado de lado mayor ha de ser
igual a la suma de los cuadrados de los dos menores.
Determinar si el triángulo es rectángulo.
A p l i ca ci o ne s del t e or em a d e Pitá g o r a s . E je r ci cio s
1
La hipotenusa de un triángulo rectángulo mide 405.6 m y la
proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.
2
Calcular los lados de un triángulo rectángulo sabiendo que
la proyección de uno de los catetos sobre la hipotenusa es 6 cm y la
altura relativa de la misma
3
cm.
Una escalera de 10 m de longitud está apoyada sobre la
pared. El pie de la escalera dista 6 m de la pa red. ¿Qué altura
alcanza la escalera sobre la pared?
4
Determinar el lado de un triángulo equilátero cuyo perímetro
es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus
áreas?
5Calcular
el área de un triángulo equilátero inscrito en una
circunferencia de radio 6 cm.
6
Determinar
el
área
del
cuadrado
inscrito
en
una
circunferencia de longitud 18.84 cm.
7
este
En un cuadrado de 2 m de lado se inscribe un círculo y en
círculo
un
cuadrado
y
en
este
otro
círculo.
Hallar
el
área
comprendida entre el úl timo cuadrado y el último círculo.
8
bases
El perímetro de un trapecio isósceles es de 110 m, las
miden
40
y
30
m
respectivame nte.
Calcular
los
lados
no
paralelos y el área.
9
A un hexágono regular 4 cm de lado se le inscribe una
circunferencia y se le circunscribe otra. Hallar el área de la corona
circular así formada.
10
En una circunferencia una cuerda mide 48 cm y dista 7 cm
del centro. Calcular el área del círculo.
11
Los catetos de un triángulo inscrito en una circunferencia
miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la
circunferencia y el área del círculo.
12
Sobre un círculo de 4 cm de radio se traza un ángulo
central de 60°. Hallar el área del segmento circular comprendido
entre la cuerda que une los extremos de los dos radios y su arco
correspondiente.
A p l i ca ci o ne s del t e or em a d e Pitá g o r a s . E je r ci cio s
1
La hipotenusa de un triángulo rectángulo mide 405.6 m y la
proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.
2
Calcular los lados de un triángulo rectángulo sabiendo que la
proyección de uno de los catetos sobre la hipotenusa es 6 cm y la
altura relativa de la misma
3
cm.
Una escalera de 10 m de longitud está apoyada sobre la
pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura
alcanza la escalera sobre la pared?
4
Determinar el lado de un triángulo equilátero cuyo perímetro
es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus
áreas?
5
Calcular el área de un triángu lo equilátero inscrito en una
circunferencia de radio 6 cm.
6
Determinar
el
área
del
cuadrado
inscrito
en
una
circunferencia de longitud 18.84 cm.
7
este
En un cuadrado de 2 m de lado se inscribe un círculo y en
círculo
un
cuadrado
y
en
este
otro
círculo.
Hallar
el
área
comprendida entre el último cuadrado y el último círculo.
8
bases
El perímetro de un trapecio isósceles es de 110 m, las
miden
40
y
30
m
respectivamente.
Calcular
los
lados
no
paralelos y el área.
9
A un hexágono regular 4 cm de lado se le inscribe una
circunferencia y se le circunscribe otra. Hallar e l área de la corona
circular así formada.
10
En una circunferencia una cuerda mide 48 cm y dista 7 cm
del centro. Calcular el área del círculo.
11
Los catetos de un triángulo inscrito en una circunferencia
miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la
circunferencia y el área del círculo.
12
Sobre un círculo de 4 cm de radio se traza un ángulo
central de 60°. Hallar el área del segmento circular comprendido
entre la cuerda que une los extremos de los dos radios y su arco
correspondiente.
Te o r em a d e Pitá g o r a s . E je r ci cio s
Examen
1
Dado un triángulo equilátero de 6 m de lado, hallar el área
de uno de los sectores determinado por la circunferencia circunscrita
y por los radios que pasan por los vértices.
2
Calcular el área de la corona circular determinada por las
circunferencias
inscrita
y
circunscrita
a un
cuadrado
de
8
m
de
isósceles
se
diagonal.
3
Si
los
lados
no
paralelos
de
un
trapecio
prolongan, quedaría formado un triángulo equilátero de 6 cm de
lado.
Sabiendo
que
el
trapecio
tiene
la
mitad
de
la
altura
del
triángulo, calcular el área del trapecio.
4
El área de un cuadrado es 2304 cm². Calcular el área del
hexágono regular que tiene su mismo perímetro.
5En
una circunferencia de radio igual a 4 m se inscribe un
cuadrado y sobre los lados de este y hacia el exterior se construyen
triángulos equiláteros. Hallar el área de la estrella as í formada.
Cuadriláteros
Defincion de cuadrilátero .- Los cuadriláteros son polígonos de cuatro lados.
La suma de los ángulos interiores de un cuadrilátero es igual a 360°.
Clasificación de cuadriláteros
Paralelogramos
Cuadriláteros que tienen los lado s paralelos dos a dos. Se
clasifican en:
Cuadrado
Tiene los 4 lados iguales y los 4 ángulos rectos.
Rectángulo
Tiene lados iguales dos a dos y los 4 ángulos rectos.
Rombo
Tiene los cuatro lados iguales.
Romboide
Tiene lados iguales dos a d os.
Trapecios
Cuadriláteros que tienen dos lados paralelos, llamados base mayor y base
menor. Se clasifican en:
Trapecio rectángulo
Tiene un ángulo recto.
Trapecio isósceles
Tiene dos la dos no paralelos iguales.
Trapecio escaleno
No tiene ningún lado igual ni ángulo recto.
Trapezoides
Cuadriláteros que no tiene ningún lado igual ni paralelo.
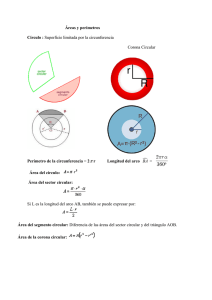
Circunferencia y círculo. Resumen
Circunferencia
Es una línea curva cerrada cuyos puntos e stán todos a la
misma distancia de un punto fijo llamado centro.
Elementos de la circunferencia
Centro
Punto
del
que
equidistan
todos
los
puntos
de
la
circunferencia.
Radio
Segmento que une el centro de la circunferencia con un punto
cualquiera de la misma.
Cuerda
Segmento que une dos puntos de la circunferencia.
Diámetro
Cuerda que pasa por el centro.
Arco
Cada
una
de
circunferencia. Se
las
partes
en
suele
asociar
a
que
cada
una
cuerda
cuerda
el
divide
menor
arco
delimita.
Semicircunferencia
Cada uno de los arcos iguales que abarca un diámetro.
a
la
que
Círculo
Es
la
figura
plana
comprendida
en
el
interior
de
una
y
el
arco
y
el
arco
circunferencia.
Elementos de un círculo
Segmento circular
Porción
de
círculo
limitada
por
una
círculo
limitada
por
un
cuerda
correspondiente.
Semicírculo
Porción
del
diámetro
correspondiente . Equivale a la mitad del círculo.
Zona circular
Porción de círculo limitada por dos cuerdas.
Sector circular
Porción de círculo limitada por dos radios.
Corona circular
Porción de círculo l imitada por dos círculos concéntricos.
Trapecio circular
Porción
de
círculo
limitada
por
dos
radios
y
una
corona
circular.
Posiciones relativas de un punto respecto a una
circunferencia
Interior
Punto sobre la circunferencia.
Punto exterior a la circunfere ncia
Posiciones relativas de una recta y una
circunferencia
Recta secante
Recta tangente
Recta exterior
Posiciones relativas de dos circunferencias
Ningún punto en común
Exteriores
Interiores
Concéntricas
Un punto común
Tangentes exteriores
Tangentes interiores
Dos puntos en común
Secantes
Ángulos en la circunferencia
Ángulo
central.-
La
medida
de
un
arco
es
la
de
su
ángulo
central
correspondiente.
Ángulo inscrito .- Mide la mitad del arco que abarca.
Ángulo semiinscrito.- Mide la mitad del arco que abarca .
Ángulo interior .- Mide la mitad de la suma de las medidas de los arcos que
abarcan sus lados y las prolongaciones de sus lados .
Ángulo exterior .- Mide la mitad de la diferencia entre las medidas de los arcos
que abarcan sus lados sobre la circunferencia.
Áreas
Longitud de una circunferencia
Longitud de un arco de circunferencia
Área de un círculo
Área de un sector circular
Área de una corona circular
Área de un trapecio circular
Área de un segmento circular
Área del segmento circular AB = Área del sector circular AOB
− Área del triángulo AOB
Circunferencia y círculo. Ejercicios
1
La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido
el camión cuando la rueda ha dado 100 vueltas?
2
Un faro barre con su luz un ángulo plano de 128°. Si e l alcance
máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del
arco correspondiente?
1 milla = 1 852 m
3
La longitud de una circunferencia es 43.96 cm. ¿Cuál es el área
del círculo?
4
El área de un sector circular de 90° es 4 π cm. Calcular el radio
del círculo al que pertenece y la longitud de la circunferencia.
5
Hallar el área de un sector circular cuya cuerda es el lado del
triángulo equilátero inscrito, siendo 2 cm el radio de la circunferencia.
6
Dadas
dos
circunferencias
concéntri cas
de
radio
8
y
5
cm,
respectivamente, se trazan los radios OA y OB, que forman un ángulo de
60°. Calcular el área del trapecio circular formado.
7
En un parque de forma circular de 700 m de radio hay situada en
el centro una fuente, también de forma circ ular, de 5 m de radio. Calcula
el área de la zona de paseo.
8 La
superficie de una mesa está formada por una parte central
cuadrada de 1 m de lado y dos semicírculos adosados en dos lados
opuestos. Calcula el área.
9 Calcula
el área de la parte sombreada, si el radio del círculo mayor
mide 6 cm y el radio de los círculos pequeños miden 2 cm.
10
Calcula el área de la parte sombreada, siendo AB = 10 cm, ABCD
un cuadrado y APC Y AQC arcos de circunferencia de centros B y D.
Circunferencia y círculo. Ejercici os resueltos
1
La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido el
camión cuando la rueda ha dado 100 vueltas?
r = 90 : 100 = 0.9 m
L = 2 ·
π · 0.9 = 5.65 m
5.65 · 100 = 565 m
Circunferencia y círculo. Ejercicios resueltos
2
Un faro barre con su luz un ángulo plano de 128°. Si el alcance
máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del
arco correspondiente?
1 milla = 1 852 m
Circunferencia y círculo. Ejercicios resueltos
3
La longitud de una circunferencia es 4 3.96 cm. ¿Cuál es el área del
círculo?
Circunferencia y círculo. Ejercicios resueltos
4
El área de un sector circular de 90° es 4 π cm. Calcular el radio del
círculo al que pertenece y la longitud de la circunferencia.
Circunferencia y círculo. Ejercicios resueltos
5
Hallar el área de un sector circular cuya cuerda es el lado del
triángulo equilátero inscrito, siendo 2 cm el radio de la circunferencia.
Circunferencia y círculo. Ejercicios resueltos
6
Dadas
dos
circunferencias
concéntricas
de
radio
8
y
5
cm,
respectivamente, se trazan los radios OA y OB, que forman un ángulo de
60°. Calcular el área del trapecio circul ar formado.
Circunferencia y círculo. Ejercicios resueltos
7
En un parque de forma circular de 700 m de radio hay situada en el
centro una fuente, también de forma circular, de 5 m de radio. Calcula el
área de la zona de paseo.
Circunferencia y círculo. Ejercicios resueltos
8
La superficie de una mesa está formada por una parte central
cuadrada de 1 m de lado y dos semicírculos adosados en dos lados
opuestos. Calcula el área.
Circunferencia y círculo. Ejercicios resueltos
9
Calcula el área de la parte sombreada, si el radio del círculo mayor
mide 6 cm y el radio de los círculos pequeños miden 2 cm.
Circunferencia y círculo. Ejercicios resueltos
10
Calcula el área de la parte sombreada, siendo AB = 10 cm, ABCD un
cuadrado y APC Y AQC arcos de circunferencia de centros B y D.
La parte sombreada se compone de dos segmentos circulares.
Área del segmento circular = Área del sector circular − Área
del triángulo.
Circunferencia y círculo. Ejercicios
1
Ana se ha mont ado en el caballo que está a 3.5 m del centro de
una plataforma que gira y su amiga Laura se ha montado en el león que
estaba a 2 m del centro. Calcular el camino recorrido por cada una cuando
la plataforma ha dado 50 vueltas.
2
Los brazos de un columpio m iden 1.8 m de largo y pueden
describir como máximo un ángulo de 146°. Calcula el espacio recorrido
por el asiento del columpio cuando el ángulo descrito en su balanceo es el
máximo.
3
Hallar el área del sector circular cuya cuerda es el lado del
cuadrado i nscrito, siendo 4 cm el radio de la circunferencia.
4
Calcula el área sombreada, sabiendo que el lado de cuadrado es 6
cm y el radio del círculo mide 3 cm.
5
En una plaza de forma circular de radio 250 m se van a poner 7
farolas cuyas bases son círculos de un 1 m de radio, el resto de la plaza lo
van a utilizar para sembrar césped. Calcula el área del césped.
Áreas de polígonos. Ejercicios
1 Un
campo rectangular tiene 170 m de base y 28 m de altura.
Calcular:
1 Las hectáreas que tiene.
2 El precio del campo si el metro cuadrado cuesta 15 €.
2
En el centro de un jardín cuadrado de 150 m de lado hay una
piscina también cuadrada, de 25 m de largo. Calcula el área del jardín.
3
Hallar el área de un triángulo rectángulo isósceles cuyos lados
miden 10 cm cada uno.
4
Calcula el número de árboles que pueden plantarse en un terreno
rectangular de 32 m de largo y 30 m de ancho si cada planta necesita
para desarrollarse 4 m².
5
El área de un trapecio es 120 m², la altura 8 m, y la base menor
mide 10 m. ¿Cuánto mide la otra base?
6
Calcula el área del cuadrado que resulta de unir los puntos medios
de los lados de un rectángulo cuya base y altur a miden 8 y 6 cm.
7
Calcular el área de un paralelogramo cuya altura mide 2 cm y su
base mide 3 veces más que su altura.
8
Cuánto vale el área de la parte subrayada de la figura, si el área
del hexágono es de 96 cm².
9
Calcula el área de un rombo cuya diagonal mayor mide 10 cm y
cuya diagonal menor es la mitad de la mayor.
10
Una zona boscosa tiene forma de trapecio, cuyas bases mi den
128 m y 92 m. La anchura de la zona mide 40 m. Se construye un paseo
de 4 m de ancho perpendicular a las dos bases. Calcula el área de la zona
arbolada que queda.
Áreas. Evaluación
Examen
1
Calcula el número de baldosas cuadradas, de 10 cm, de lado que
se necesitan para enlosar una superficie rectangular de 4 m de base y 3 m
de altura.
2
Un jardín rectangular tiene por dimensiones 30 m y 20 m. El
jardín está atravesado por dos caminos perpendiculares que forman una
cruz. Uno tiene un ancho de 8 dm y el otro 7 dm. Calcula el área del
jardín.
3
El perímetro de un triángulo equilátero mide 0.9 dm y la altura
mide 25.95 cm. Calcula el área del triángulo.
4
Dado el cuadrado ABCD, de 4 m de lado, se une E, punto medio
del segmento BC, con el vértice D. Calcular el área del trapecio formado.
5
Calcula la cantidad de pi ntura necesaria para pintar la fachada de
este edificio sabiendo que se gastan 0.5 kg de pintura por m 2 .