PROBLEMA 1

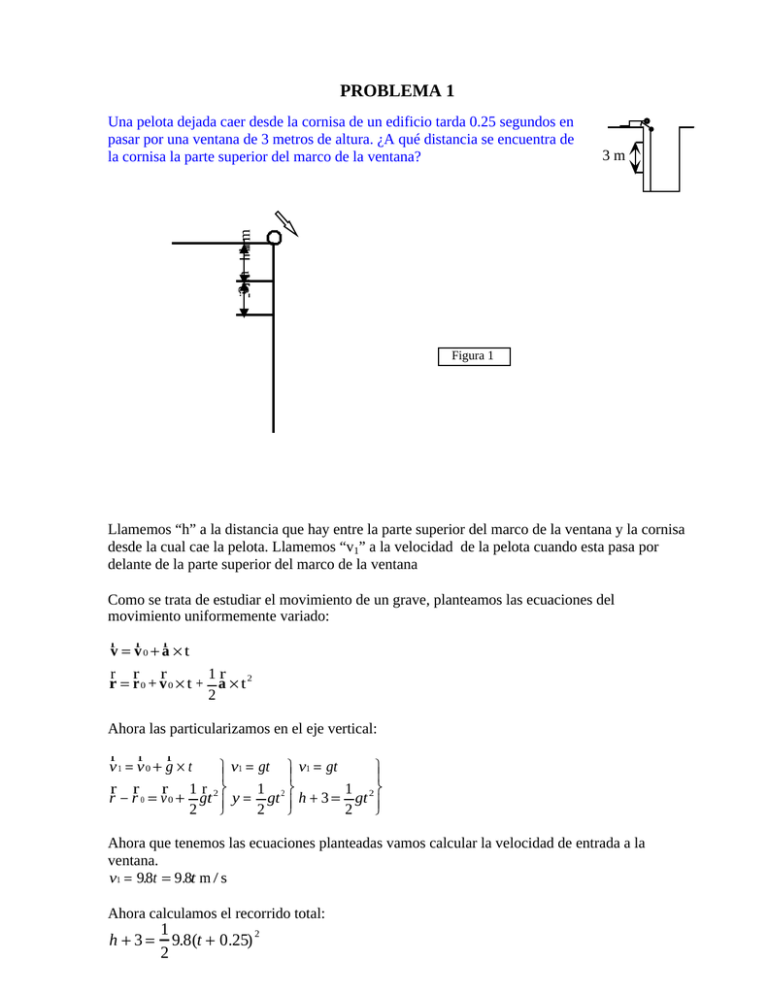
PROBLEMA 1
3m
3m
hm
Una pelota dejada caer desde la cornisa de un edificio tarda 0.25 segundos en
pasar por una ventana de 3 metros de altura. ¿A qué distancia se encuentra de
la cornisa la parte superior del marco de la ventana?
Figura 1
Llamemos “h” a la distancia que hay entre la parte superior del marco de la ventana y la cornisa
desde la cual cae la pelota. Llamemos “v1” a la velocidad de la pelota cuando esta pasa por
delante de la parte superior del marco de la ventana
Como se trata de estudiar el movimiento de un grave, planteamos las ecuaciones del
movimiento uniformemente variado:
r r r
v = v0 + a × t
r r r
1r 2
r = r0 + v0 × t + a × t
2
Ahora las particularizamos en el eje vertical:
r r
r
v1 = v0 + g × t
 v1 = gt  v1 = gt




r r
r 1 r 2
1 2
1 2
r − r 0 = v 0 + gt  y = gt  h + 3 = gt 
2

2

2

Ahora que tenemos las ecuaciones planteadas vamos calcular la velocidad de entrada a la
ventana.
v1 = 98
. t = 9.8t m / s
Ahora calculamos el recorrido total:
h +3=
1
2
9.8(t + 0.25)
2
Por último calculamos el recorrido sobre la ventana:
1
3 = 9.8t × 0.25 + 9.8 × 0.252 ⇒ 3 = 2.45t + 0.30625 ⇒ t = 1.0995 s
2
Volviendo a la ecuación del recorrido total:
1
1
h + 3 = 9.8(10995
.
+.025) 2 ⇒ h = 98
. (10995
.
+ 0.25) 2 − 3 = 5.9236 m
2
2
PROBLEMA 2
ÿ
ÿ El maquinista de un tren de viajeros que lleva una
10 m/s
30 m/s
velocidad de 30m/s, ve un tren de mercancías
cuyo furgón de cola se encuentra a 100 m delante
100 m
en la misma vía. El tren de mercancías avanza en
el mismo sentido que el de viajeros, con una velocidad de 30m/s. El maquinista del tren de
viajeros aplica inmediatamente los frenos, produciendo una deceleración constante de 1
m/s2 , mientras que el tren de mercancías continua su marcha a velocidad constante.
a) ¿Chocaran ambos trenes?
b) En caso de producirse el choque, ¿dónde tendrá lugar?.
Solución:
( 100+x)
A
v = 30 m/s
B
v= 10 m/s
100 m
TREN A:
V = 30 m/s
S = (100+x)
A = -1 m/s2
Planteamos las ecuaciones del movimiento uniformemente variado:
vf2 = vi2 +2.a.s
vf = vi + a. t2
x = x0 +v0 .t + _ a.t2
TREN B:
V=cte=10 m/s
Formulamos las ecuaciones del movimiento uniforme:
x = v.t
v = x/t
El espacio x recorrido por el tren B que lleva una velocidad constante es:
x = v.t
x= 10.t
El tren A que se desplaza con una cierta deceleración necesita recorrer en el mismo tiempo t el
espacio x que recorre el tren B mas los 100 m que separan a ambos. Por lo tanto el espacio que debe
recorrer para alcanzar al otro tren será s=(100+x).
Como se trata de un movimiento uniformemente variado la ecuación del espacio es:
s= v0.t + 1/2 a.t2
(100 + x)= 30.t + _ (-1) t 2
Siendo x=10.t sustituimos en la ecuación anterior,
100 + 10.t = 30.t + _ (-1)a.t2
t2 -40.t + 200= 0
Resolvemos la ecuación de segundo grado y llegamos a la conclusión de que los dos trenes se
chocan dos veces.
t1=34.1 s
t2=5.86 s
La respuesta correcta es t2 porque corresponde a la primera vez que se chocan los dos trenes.
Según esto sustituimos el tiempo obtenido t 2 en la ecuación x= 10. t
x=10(5.86)= 58.6 m recorre el tren B hasta que chocan.
El espacio recorrido por el tren A era igual a (100+x) .Con el valor de x hallado realizamos la
ultima operación.
s=(100+ 58.6)= 158.6 m recorre el tren A hasta que chocan.
PROBLEMA 3
x0 = -3 m
1
2 t (s)
a)
x (t)
10
5
0
-5
x (m)
4
2
0
-2
x (m)
v (t)
v (m/s)
Tres partículas describen los movimientos
unidimensionales representados en las
figuras. Determinar en cada caso las
características del movimiento (
x0 ,x,v0 ,v,a y tipo de movimiento).
Representar para cada una de ellas x(t),
v(t), y a(t).
20 t (s)
10
b)
6
4
2
0
-2
x (t)
2
c)
a) X0 = -3 m; es un dato que nos da el problema.
V0 = -2 m/s; para t=0, V=-2.
La pendiente de la recta tangente a esa curva es ∆Y/∆X=2/1=2; esto significa que dv/dt=2; es
decir a=2 m/s2 .
Sabemos que V=V0 +at; luego… V=(-2+2t) m/s
Integrando la velocidad, obtendremos la posición, así que…
2
2
X= ∫ Vdt = ∫ − 2 + 2tdt = −2t + t + C = (− 3 − 2t + t ) m
Se trata pues de un MRUA
v- t
x-t
12
Velocidad (m/s)
Posición (m)
15
10
5
0
10
8
6
4
2
1
2
3
4
5
0
-5
1
2
3
tiempo (s)
a-t
2
aceleración (m/s )
4
tiempo (s)
2,5
2
1,5
1
0,5
0
1
2
3
4
5
tiempo (s)
b) X0 =5 m; ⇒ para t=0 X=5
6
7
8
5
6
4 t (s)
La pendiente de la gráfica es 5/10=1/2, pero la curva, en este caso recta, es decreciente, luego la
pendiente realmente es –1/2. Es decir, V= -1/2 m/s (es constante), por lo tanto V0 = -1/2 m/s
Derivando V, obtenemos a, dV/dt=a=0 (derivada de una cte.)
Por el contrario, si integramos V, obtenemos que X = ((−1 / 2)t + 5) m
X = ∫ Vdt = ∫ − 1 / 2 = −(1 / 2)t + C = ( − (1/ 2)t + 5) m
Se trata pues de un MRU
x-t
5
0
1
-0,2
2
3
4
5
6
-0,4
Posición (m)
velocidad (m/s)
v-t
4
3
2
1
0
-0,6
1
2
3
tiempo (s)
4
5
6
7
tiempo (s)
a-t
aceleración (m/s2)
1
0,8
0,6
0,4
0,2
0
1
2
3
4
5
6
tiempo (s)
c) X0 = -2; ⇒para t = 0 X= -2
La curva, es una parábola de vértice (0,-2), es decir, es del tipo, y=-2+bt2 . Calcularemos b de la
siguiente forma:
Para t = 4 s, x = 6 m
6 = −2 + b ⋅ 4 2 ‡ b = 1 / 2
Por lo tanto X = (−2 + 1 / 2 ⋅ t 2 ) m
V= dx / dt = t m/s, así que V0 =0
a= dv / dt = 1 m/s2
Es por tanto, un MRUA
x-t
25
20
p
15
o
si
ci 10
ó
n 5
(
m 0
)
1
-5
a-t
2
3
1,2
a4
15
c
el 0,8
tiempo(s)
er ,
06
a
ci 0,4
ó 0,2
n
0
(
1
m
/s
2)
6
7
v -t
2
3
4
5
6
7
tiempo (s)
v
e
l
o
c
i
d
a
d
(
m
/
s
)
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
tiempo(s)
PROBLEMA 4
La aceleración de una partícula que describe un movimiento unidimensional es: a=sen t
m/s . Si para t=0 x=0.Calcular y representar v(t) y x(t) cuando (a) v(0)=0 y (b)v(0)=-1
m/s2 .¿Describirá la partícula un movimiento oscilatorio?
2
Solución:
I.- Hallamos la expresión de la velocidad calculando la integral de la aceleración:
a=sen t(m/s2 ), t=0 , x=0 → V=∫ sen tdt= -cost + c
II.- Si v(0)=0 m/s , y sustituimos este valor , nos queda lo siguiente:
0=-cos 0 + c1 → c1 =0 + cos 0 → c1 =1
7
III.- Si v(0)=-1 m/s, y sustituimos otra vez :
-1=-cos 0 + c2 → c2 =-1 + cos 0 → c2 =0
IV.- Con el valor de las constantes , podemos hallar ya las expresiones de la velocidad:
(a) v1 =-cos t + 1
(b) v2 =-cos t + 0
V.- Para hallar las expresiones de la posición, tenemos que tener en cuenta que:
V=dx/dt → dx=V.dt → x=∫ V.dt → x=∫ (-cost + c).dt
(a) x=∫ (-cost + 1) dt → x= t – sen t + c3 . Para x=0, t=0 → c3 =0
(b) x=∫ (-cost)dt → x= -sen t + c4 . Para x=0, t=0 → c4 =0
VI.- Por tanto:
(a)x1 = t – sen t
(b)x2 =-sent
VII.-Los gráficos de las expresiones de las velocidades, son, respectivamente:
v1 = 1 – cos t
V2 = -cos t
VIII.- Los gráficos de las
posiciones, son, respectivamente:
x1 =t – sen t
x2 = - sen t
PROBLEMA 5
La aceleración de un cuerpo que se mueve en línea recta está dada por a= 4-t2 donde a se
mide en m/s2 y t en s. Encontrar las expresiones de la velocidad y el desplazamiento en
función del tiempo suponiendo que para t=3 , v=2 m/s y x=9m.
a=dv/dt
a·dt=dv
∫(4-t2 )·dt=∫dv
4t-t3 /3 +c=v
t=3 v=2 4*3-9+c=2 c=-1 V=-t3 /3+4t-1
v=dx/dt
(-t3 /3+4t-1)=dx
∫(-t3 /3+4t-1)dt=∫dx
(-1/3)t4 /4+4t2 /2-t+k=x t=3 x=9
(-1/3)·(81/4)+2·9-3+k=9 k=3/4
x=(-1/12)t4 +2t2 -t+3/4
PROBLEMA 6
La aceleración de una partícula que se mueve en línea recta viene dada por a= kv2 , donde k es una constante. Suponiendo que cuando t=0, v=v0 y x=x0,
encontrar la velocidad y el desplazamiento en función del tiempo y la velocidad
en función del desplazamiento
a=
⇒
v dv
t
dv
⇒ dv = a ⋅ dt ⇒ dv = − k ⋅ v 2dt ⇒ ∫ − 2 = ∫ kdt ⇒
v0 v
0
dt
v
 1  = k [t ]v ⇒
0
 v v 0
1 1
1 1
1
−
= k (t − 0) ⇒ =
+ kt ⇒ ELRESULTADOES : v =
v v0
v v0
1/ v0 + kt
t
t
1  1
x
t
dx
1

1  1

v=
⇒ ∫ dx = v ⋅ dt = ∫
⋅ dt ⇒ [ x ]xx 0 =  ln  + k ⋅ t   ⇒ x − x0 = ln  + k ⋅t   ⇒
x0
0 1/ v0 + kt
dt
 0
k   v0
 0
 k  v0
⇒ x − x0 =

 1

1  1
1  1 / v0 + k ⋅ t 
1
 = x 0 + ln (1 + ktv0 )
ln + k ⋅ t  − ln  + 0 → ELRESULTADOES : x = x0 + ln
k   v0
k  1/ v0 
k

 v0

En cuanto a la velocidad en función del desplazamiento:
a=
dv dx dv
dv
⋅
=
⋅ v ⇒ Yaquelaaceleraciónes = − kv 2 porlotanto ⇒ −k ⋅ v 2 =
⋅v ⇒
dx dt dx
dx
⇒ −k ⋅ v =
v dv
dv
⇒∫
=
v0 v
dx
∫
x
x0
− k ⋅ dx ⇒ sabiendoque
⇒ ln v − ln v0 = −k (x − x 0 )⇒ ln
dv
v
x
es ln dev ⇒ [ln v ]v0 = −k [x ]x0 ⇒
v
v
v
− k (x − x0 )
= −k (x − x0 )⇒
=e
→ ELRESULTADOES :
v0
v0
v = v0 ⋅ e
− k ( x −x 0 )
PROBLEMA 7
Un punto se mueve en el plano XY de manera que Vx = 4t3 + 4t,
Vy = 4t.
Si la posición del punto es (1,2) cuando t=0, encontrar la ecuación cartesiana
de la trayectoria.
⇒ ∫dx = ∫vx dt +C1
vx = dx/dt
Como no se ponen limites aparecen constantes de integración
∫dx =∫4t3 + 4t
vy = dy/dt
⇒ x = 4t4/4 + 4t2/2 + C1 = t4 +2t2 +C1
⇒ ∫dy = ∫vy dt +C2 ⇒
∫ dy = ∫4t +C2 ⇒
y=4t2/2 + C2 = 2t2 +C2
Si t= 0 ⇒ x=1 luego 1= 04 + 2 02 + C1 ⇒ C1 =1 ⇒ x= t4 + 2t2+1
Si t= 0 ⇒ y=2 luego 2= 2 02 + C2 ⇒ C2=2 ⇒ y= 2t2 +2
Para hallar la ecuación de la trayectoria, tenemos que despejar la t en la x y
sustituirlo en la otra.
Llamamos f=t2 ⇒ f2 +2f + (1-x) = 0 f= -2 ±(4-4(1-x))1/2
2
2
f= -1 ±√x = t
Ahora sustituyo en la y
Y = 2 (-1 ±√x) +2 = ± 2√x
La solución es: Y= ± 2√x
PROBLEMA 9
Encontrar el radio de curvatura en el pto más alto de la trayectoria de un proyectil disparado
con una velocidad Vo y haciendo un ángulo α con la horizontal.
y
Vy = 0
an
Vy
α
ρ
x
Vx
En el pto más alto de la trayectoria la componente Vy es cero, y solo tenemos Vx, además
at=0, y la aceleración se reduce a aN , que en este caso coincide con la gravedad.
Vx = Vo · cos α que se mantiene constante a lo largo de toda la trayectoria
2
aN = g
siendo
siendo
aN = g
aN = V / ρ _ ρ =
2
V/
aN
y V = Vx el resultado final es:
2
ρ=
(Vo · cos α )
g
PROBLEMA 10
Un avión bombardero está volando horizontalmente a una altura de 1.2Km
con una velocidad de 180Km/h.
a) ¿Cuánto tiempo antes de que el avión esté sobre el blanco debe
dejar caer la bomba?
Vo =180 Km/h = 180 ∗ (1000/3600) =50 i m/s
a = -g j m/s2
v = ∫ a∗dt = -gt j + vo = 50 i –gt j
s = ∫ v∗dt = 50t i – (1/2)∗gt 2 j + so = 50t i + (1200 – 1/2∗gt2) j
Estas son las ecuaciones del movimiento de la bomba. Para calcular cuánto
tiempo antes tiene que dejar caer la bomba le obligamos a que Sy =0
Sy = 0 = 1200 – 1/2∗gt2 ⇒
t = [(1200∗2)/g]1/2 = 15.64s
Este es el tiempo que nos piden que en definitiva es el tiempo que tarda la
bomba en caer al suelo.
b) ¿Cuál es la distancia horizontal cubierta por la bomba?
Nos están pidiendo la Sx.
Sx = 50t = 50 ∗ 15.64 = 782.4m
c) ¿Cuál es la velocidad de la bomba al llegar al suelo?
Para este apartado tenemos que tener en cuenta lo calculado en el primero y
es que el tiempo que tarda la bomba en caer al suelo es de 15.64s
Calculamos entonces la velocidad a los 15.64s
v = 50 i – gt j
v(15.64) = 50 i – (9.81 ∗ 15.64) j = 50 i – 153.44 j
Ahora calculamos el modulo de la velocidad:
v= (502 + 153.442)1/2 = 161.38m/s
161.38m/s = 161.38m/s ∗ [(3600s/h) / (1000m/Km)] = 580.9Km/h
d)¿Cuál es el ángulo que forma con el eje horizontal la velocidad de la
bomba al caer al suelo?
tgα = senα / cosα = vy / vx = ±153.44 / 50 = - 3.06 ⇒ α = - 71.9˚
e)¿Cuál es la velocidad de la bomba 10s después de soltarla?
Nos están pidiendo la velocidad de la bomba cuando t = 10s
v = 50i - gtj
v(10) = 50i - (9.81∗10)j = 50i – 98.1j m/s
Ahora calculamos el modulo de esta velocidad:
v = (50 2 + 98.12)1/2 = 110m/s
110m/s = 110m/s ∗[(3600s/h) / (1000m/Km)] = 396.38Km/h
f)¿Cuál es la velocidad de la bomba cuándo se encuentran a 200m de
altura?
Tenemos que calcular la velocidad de la bomba cuando Sy = 200m. Para
ellos primero tenemos que ver el tiempo que tarda la bomba en estar a 200m de
altura.
Sy = 200 = 1200 – 1/2gt2 ⇒ t = [(1000∗2) / 9.81]1/2 = 14.27 s
Ahora con este tiempo calculamos la velocidad:
v = 50i – gt2
v(14.27) = 50 i – (9.81∗14.27) j = 50 i – 140 j
Y calculamos el módulo de la velocidad:
v= (502 + 1402)1/2 = 148.7m/s
148.7m/s = 148.7m/s ∗[(3600s/h) / (1000m/Km)] = 535Km/h
PROBLEMA 11
Un proyectil es disparado con una velocidad de 600 m/s haciendo un ángulo de 60º con la
horizontal. Calcular:
a)
b)
c)
d)
El alcance horizontal
La altura máxima
La velocidad y la altura después de 30 s
La velocidad y el tiempo cuando el proyectil se encuentra a 10 Km de altura
SOLUCION
Se trata de un tiro parabólico clasico. Las ecueaciones para resolver tiros
parabólicos son:
Vx=V.cos θ
Vy=V.sen θ+g.t
X=Vx.t
Y=Vy.t – .g.t2
a)
para calcular el alcance horizontal ( x ) es necesario conocer el tiempo que tarda el caer
( o el tiempo que tarda en alcanzar la altura máxima , porque el movimiento es simétrico) y la
Vx
Vx= V. Cos θ
θ= 60º
Vo = 600 m/s
Vx = 600 m/s .cos 60º = 300 m/s
Para calcular el tiempo que tarda en caer se utiliza la formula de la Vy porque cuando Vy=0, el
proyectil se encuentra en lo más alto. Ese tiempo es la mitad que el tiempo que tarda en caer.
Vy=Vo. Sen θ + g.t
Vy = 0 =600 m/s. Sen60º + 9,8 m/s’2 . t1 →t1 = 53,02 s
→t = 2. t1 = 106, 0439 s
El alcance aplicando la formula es:
X= V0.cos θ .t = Vx.t = 300 m/s . 106, 0439 s = 31813,17 m
b)
Para la altura máxima ( y ) se necesita la Vy y el tiempo , que ya está hallado
Y = Vy. T – g . t 2
Y = 600 m/s . sen 60º . 106, 0439 s – . 9,8 m/s2 . 106, 0439 s =13775 m
c)
Para hallar la velocidad en 30 s hay que hallar el modulo con la Vx y la Vy
____________ _________________________________________________
V= √ Vx 2 + Vy 2 = √( 600 m/s . cos 60º)2 + (600 m/s . sen60º - 9,8 m/s2 .30 s)2
=375m/s
Para hallar la altura tenemos todos los datos , solo hay que sustituir
Y= Vy . t – g . t2
Y= 600 m/s . 30 s – 9,8 m/s2 . (30 s)2 = 11178,45 m
d)
Si sabemos la altura entonces hay que hallar el tiempo
Y = 10 000 m = V0 . senθ .t – .g . t2 → _ . 9,8 . t2 – 600 . sen 60 . t + 10 000 = 0
Por la formula de resolución de ecuaciones de segundo grado se halla la t
T= 25,26 s y 80,77 s
Da dos tiempos distintos porque uno se refiere al tiempo cuando el proyectil sube y el
otro para cuando baja
Las velocidad en el eje x será la misma que la inicial
La velocidad en el eje y tiene que ser la misma pero con signo contrario por la
propiedad de simetría descrita anteriormente para esta clase de movimientos
Vx = v. Cos 60 =300 m/s
Vy = V . sen 60º - g . t2
( t = 25.26 s)
Vy = 600 . sen 60 – 9,8 . 25,26 s = 272 m/s
( t = 80.77 )
Vy = 600 . sen 60 – 9,8 . 80.77 = -272 m/s
Así que la velocidad es vectorialmente : (300 , 272 ) m/s
y
(300 , -272 ) m/s
PROBLEMA 12
Desde el pie de un plano inclinado un ángulo α sobre la
y
horizontal, se dispara un proyectil con velocidad inicial v0 y
v0
ángulo de tiro θ (θ > α).
θ
α
a) ¿Cuál es el alcance R medido a lo largo del plano
x
inclinado?
b) Comprobar que para α=0 la expresión de R se reduce a la del alcance
horizontal.
SOL : R = (v0 cosθ ) ⋅ (tgθ − tgα ) / (g ⋅ cosα )
2
x = V0x ⋅ t → t =
x
V0 x
Tgα =
y
V
1
⋅ g⋅t2 ⇒
2
V0 y ⋅ x 1
x2
g ⋅x2
y=
− ⋅ g ⋅ 2 = x ⋅ Tgθ −
V0 x
2
V0 x
2 ⋅V02 ⋅ cos 2 θ
y = V0 y ⋅ t −
θ
y
→ y = x ⋅ tg α
x
l
α
x
Para qué x las y coinciden:
x ⋅ tgα = x ⋅ tg θ −
x=
g ⋅x
g ⋅x
⇒
= tg θ − tg α
2
2
2
2
2 ⋅ V0 ⋅ cos θ
2 ⋅ V0 ⋅ cos θ
2
2 ⋅ V0 ⋅ cos θ
(tg θ − tgα )
g
2
2
x = l ⋅ cos α → l =
2 ⋅V02 ⋅ cos 2 θ
2 ⋅ V 2 ⋅ cos θ ⋅ sen θ V02
x
→l =
(tg θ − tg α ) = 0
=
(sen 2 ⋅θ )
cosα
g ⋅ cos α
g
g
PROBLEMA 13
Un volante cuyo diámetro es de 3 m está girando a 120 rpm. Calcular:
a) su frecuencia
b) el período
c) la velocidad angular
d) la velocidad lineal de un punto sobre su borde
La velocidad está en rpm, la paso a rad/s y así obtengo la velocidad angular (ω)
(120 rev/1 m) * (1 m/60 s) * (2∏ rad/1 rev) = 4∏ rad/s = ω
a)
ν=1/T
T = 2∏/ω = 1/ν ⇒ ν = ω/2∏ = 4∏/2∏ = 2 Hz
b)
T = 1/ν = 1/2 s
c)
ω = 4∏ rad/s
d)
R = 1,5 m
v = ω*R = 4∏*1.5=6∏ m/s = 18.85 m/s
PROBLEMA 14
Un volante cuyo diámetro es de 3m tiene una velocidad angular que disminuye uniformemente
de 100 rpm en t=0, hasta detenerse cuando t=4s. Calcular las aceleraciones tangencial y
normal de un punto situado sobre el borde del volante cuando t=2s.
DATOS
ωo=100 rpm cuando t = 0seg, ω=0 rpm cuando t= 4seg,. R=1.5m.
RESOLUCIÓN
100 rpm · 2π/60 s = 10.472 rad/ s
ω= ωo + αt
α= ω-ωo / t-to = ( 0 rad/ s - 10.472 rad/ s) / (4 s - s) = -2.618 rad/ s2
aT = αR = (2.618 rad / s2 ) · 1.5m = 3.927 m / s2
ω = ωo + α·t = 10.472 rad/ s + (-2.618rad/ s2 )2s = 5.236 rad/s
v = ω · R= (5.236 rad/s)·1.5 m = 7.854 m/s
aN = (v·2) / R = (7.854 m/s · 7.854 m/s)/1.5m = 41.12 m/ s2
PROBLEMA 15
Las coordenadas de un cuerpo en movimiento son :
X= 2 seno wt
Y= 2 cose wt
a) Encontrar la ecuación de la trayectoria.
Sabiendo que el vector “ r “ tiene dos componentes que son: ”x” e
“y”, y según la fórmula :
R=( x , y ) obtenemos colocando sus correspondientes valores en ella :
R= (2 seno wt , 2 cose wt )
b) Calcular el valor de la velocidad en cualquier instante.
Primero hemos de saber el valor del radio para poder sacar el de la
velocidad . Así basándonos en que: R= r seno B y que las ecuaciones
generales de “x” e “y” son : “r seno wt” y “r cose wt” respectivamente,
comparamos la primera ecuación con las de “x” e “y” con sus
respectivos valores obteniendo que el valor del radio es 2.
Una vez sacada esta cantidad ya se puede conseguir el valor de la
velocidad con la siguiente fórmula
:
V= W x R → V= W x 2; siendo entonces la velocidad igual a 2w
c) Calcular las componentes tangencial y normal de la aceleración
cualquier instante.
en
Rr
Según podemos ver en el dibujo, teniendo la componente de la
velocidad y el radio , obtenemos las componentes de la aceleración de
la siguiente manera :
at = dv / dt = d/dt(R·W) = R·dw/dt=R·α
an= v2/ϕ =W2·R2/R =W2·R
En el primer caso el ángulo α es constante por lo que la aceleración
es 0.
En el segundo caso simplemente hemos de sustituir los valores en la
fórmula queda:
.....W2·R= 2W2
d) Identificar el tipo de movimiento descrito por las ecuaciones
expuestas:
El movimiento descrito por estas ecuaciones es un movimiento circular.