Formulaire de trigonométrie

PCSI
Lycée Faidherbe
Lille
2016 – 2017
Trigonométrie
𝑥 désigne un nombre réel.
→
−𝚥 ).
Le plan est rapporté à un repère orthonormal direct (𝑂, −
𝚤 ,→
I
Rappels
1
Définition
cos(𝑥 + 2𝜋) = cos 𝑥
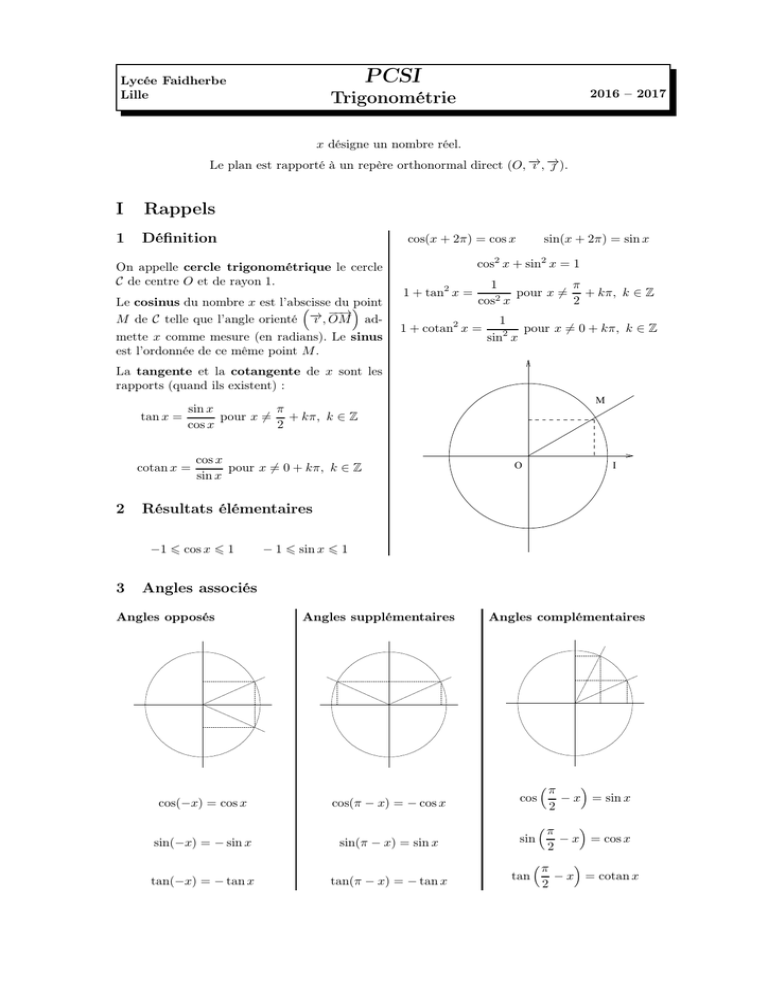
On appelle cercle trigonométrique le cercle
𝒞 de centre 𝑂 et de rayon 1.
Le cosinus du nombre 𝑥 est l’abscisse
du )
point
(
−−→
→
−
𝑀 de 𝒞 telle que l’angle orienté 𝚤 , 𝑂𝑀 ad-
mette 𝑥 comme mesure (en radians). Le sinus
est l’ordonnée de ce même point 𝑀 .
sin(𝑥 + 2𝜋) = sin 𝑥
cos2 𝑥 + sin2 𝑥 = 1
1 + tan2 𝑥 =
1
𝜋
pour 𝑥 ∕= + 𝑘𝜋, 𝑘 ∈ ℤ
cos2 𝑥
2
1 + cotan2 𝑥 =
1
pour 𝑥 ∕= 0 + 𝑘𝜋, 𝑘 ∈ ℤ
sin2 𝑥
La tangente et la cotangente de 𝑥 sont les
rapports (quand ils existent) :
M
𝜋
sin 𝑥
pour 𝑥 ∕= + 𝑘𝜋, 𝑘 ∈ ℤ
tan 𝑥 =
cos 𝑥
2
cotan 𝑥 =
2
cos 𝑥
pour 𝑥 ∕= 0 + 𝑘𝜋, 𝑘 ∈ ℤ
sin 𝑥
I
Résultats élémentaires
−1 ⩽ cos 𝑥 ⩽ 1
3
O
− 1 ⩽ sin 𝑥 ⩽ 1
Angles associés
Angles opposés
Angles supplémentaires
Angles complémentaires
cos(𝜋 − 𝑥) = − cos 𝑥
cos
(𝜋
2
)
− 𝑥 = sin 𝑥
sin(−𝑥) = − sin 𝑥
sin(𝜋 − 𝑥) = sin 𝑥
sin
(𝜋
)
− 𝑥 = cos 𝑥
tan(−𝑥) = − tan 𝑥
tan(𝜋 − 𝑥) = − tan 𝑥
cos(−𝑥) = cos 𝑥
2
)
(𝜋
− 𝑥 = cotan 𝑥
tan
2
page 2/3
Trigonométrie
Angles qui diffèrent de 𝜋
Angles qui diffèrent de
cos(𝜋 + 𝑥) = − cos 𝑥
cos
sin
sin(𝜋 + 𝑥) = − sin 𝑥
tan(𝜋 + 𝑥) = tan 𝑥
4
(𝜋
)
+ 𝑥 = cos 𝑥
2
(𝜋
2
𝑥
0
sin 𝑥
0
cos 𝑥
1
tan 𝑥
0
𝜋
6
1
2
√
3
2
√
3
3
𝜋
4
√
2
2
√
2
2
1
𝜋
3
√
3
2
1
2
√
3
)
+ 𝑥 = − cotan 𝑥
7
cos(𝑥 + 𝑦) =
cos(𝑥 − 𝑦) =
Les solutions de l’équation sont données par :
⎧
⎨ 𝑥 = 𝑎 [2𝜋]
ou
cos 𝑥 = cos 𝑎 ⇐⇒
⎩
𝑥 = −𝑎 [2𝜋]
cos 𝑥 cos 𝑦 − sin 𝑥 sin 𝑦
cos 𝑥 cos 𝑦 + sin 𝑥 sin 𝑦
sin 𝑥 cos 𝑦 + sin 𝑦 cos 𝑥
sin 𝑥 cos 𝑦 − sin 𝑦 cos 𝑥
Équation cos 𝑥 = cos 𝑎
Formules de duplication
cos(2𝑥)
sin(2𝑥)
6
tan
2
)
+ 𝑥 = − sin 𝑥
Valeurs importantes
Formules d’addition
sin(𝑥 + 𝑦) =
sin(𝑥 − 𝑦) =
5
(𝜋
𝜋
2
= cos2 𝑥 − sin2 𝑥
= 1 − 2 sin2 𝑥
= 2 cos2 𝑥 − 1
= 2 sin 𝑥 cos 𝑥
Formules de linéarisation
sin2 𝑥 =
cos2 𝑥 =
1
(1 − cos(2𝑥))
2
1
(1 + cos(2𝑥))
2
8
Équation sin 𝑥 = sin 𝑎
Les solutions de l’équation sont données par :
⎧
⎨ 𝑥 = 𝑎 [2𝜋]
ou
sin 𝑥 = sin 𝑎 ⇐⇒
⎩
𝑥 = 𝜋 − 𝑎 [2𝜋]
𝜋
2
1
0
ND
page 3/3
Trigonométrie
II
1
Compléments
4
Équation tan 𝑥 = tan 𝑎
Transformation de produits en
sommes
Les solutions de l’équation sont données par :
tan 𝑥 = tan 𝑎 ⇐⇒ 𝑥 = 𝑎 [𝜋]
2
Formules d’addition et de duplication
Quand cela a un sens :
sin 𝑎 cos 𝑏
=
cos 𝑎 cos 𝑏
=
sin 𝑎 sin 𝑏
=
tan 𝑥 + tan 𝑦
tan(𝑥 + 𝑦) =
1 − tan 𝑥 tan 𝑦
tan(2𝑥) =
3
2 tan 𝑥
1 − tan2 𝑥
5
Expression en fonction de la
tangente de l’arc moitié
(𝑥)
, on obtient quand cela
En posant 𝑡 = tan
2
a un sens :
2𝑡
tan 𝑥 =
1 − 𝑡2
2𝑡
sin 𝑥 =
1 + 𝑡2
1 − 𝑡2
cos 𝑥 =
1 + 𝑡2
III
1
1
(sin(𝑎 + 𝑏) + sin(𝑎 − 𝑏))
2
1
(cos(𝑎 + 𝑏) + cos(𝑎 − 𝑏))
2
1
(cos(𝑎 − 𝑏) − cos(𝑎 + 𝑏))
2
Tranformation de sommes en
produits
sin 𝑝 + sin 𝑞
=
sin 𝑝 − sin 𝑞
=
cos 𝑝 + cos 𝑞
=
cos 𝑝 − cos 𝑞
=
𝑝+𝑞
𝑝−𝑞
cos
2
2
𝑝+𝑞
𝑝−𝑞
cos
2 sin
2
2
𝑝−𝑞
𝑝+𝑞
cos
2 cos
2
2
𝑝−𝑞
𝑝+𝑞
sin
−2 sin
2
2
2 sin
Utilisation des complexes
Linéarisation de cos𝑚 𝜃 sin𝑛 𝜃
2
Expression de cos 𝑛𝜃 et sin 𝑛𝜃 en
fonction de cos 𝜃 et(sin)𝜃
𝑛
Utiliser les formules d’Euler :
Utiliser la formule de Moivre : 𝑒𝑖𝜃 = 𝑒𝑖𝑛𝜃 (i.e)
(cos 𝜃 + 𝑖 sin 𝜃)𝑛 = cos 𝑛𝜃 + 𝑖 sin 𝑛𝜃
𝑒 +𝑒
𝑒 −𝑒
cos 𝜃 =
et sin 𝜃 =
Développer le terme de gauche de l’égalité à
2
2𝑖
Développer (formule du binôme), regrouper puis l’aide de la formule du binôme, puis en idenfaire apparaître des cos 𝑘𝜃 et sin 𝑘𝜃 grâce aux tifiant les parties réelles et imaginaires, tirer
cos 𝑛𝜃 et sin 𝑛𝜃 comme une combinaison de proformules d’Euler. Exemples :
duits de cos 𝜃 et sin 𝜃.
3
1
Exemples :
cos 3𝜃 + cos 𝜃
cos3 𝜃 =
4
4
cos 3𝜃 = cos3 𝜃 − 3 cos 𝜃 sin2 𝜃 = 4 cos3 𝜃 − 3 cos 𝜃
1
3
3
sin 𝜃 = − sin 3𝜃 + sin 𝜃
sin 3𝜃 = 3 sin 𝜃 cos2 𝜃 − sin3 𝜃 = 3 sin 𝜃 − 4 sin3 𝜃
4
4
Compléments :
3 1
1
𝜃
𝜃
cos4 𝜃 =
+ cos 2𝜃 + cos 4𝜃
1 + 𝑒𝑖𝜃 = 2 cos( 𝜃2 )𝑒𝑖 2 et 1 − 𝑒𝑖𝜃 = −2𝑖 sin( 𝜃2 )𝑒𝑖 2
8 2
8
D’où l’on tire, en prenant les parties réelles :
1
3 1
− cos 2𝜃 + cos 4𝜃
sin4 𝜃 =
1 + cos 𝜃 = 2 cos2 ( 𝜃2 ) et 1 − cos 𝜃 = 2 sin2 ( 𝜃2 )
8 2
8
1
1
1
sin 𝜃 +
sin 3𝜃 −
sin 5𝜃
cos2 𝜃 sin3 𝜃 =
8
16
16
𝑖𝜃
−𝑖𝜃
𝑖𝜃
−𝑖𝜃
PCSI1 - PCSI2
tan(𝑥) =
Formulaire de trigonométrie - résumé
sin(𝑥)
𝜋
définie si 𝑥 ∕=
(𝜋)
cos(𝑥)
2
cos2 (𝑥) + sin2 (𝑥) = 1 1 + tan2 (𝑥) =
cos (𝜋 − 𝑥) = − cos(𝑥)
cos
sin (𝜋 − 𝑥) = sin (𝑥)
sin
(𝜋
2
(𝜋
tan (𝜋 − 𝑥) = − tan (𝑥) tan
Valeurs remarquables :
𝜋
0 𝜋6
4
√
cos
1
sin
0
tan 0
3
2
1
2
√
3
3
√
2
2
√
2
2
1
2
(𝜋
2
𝜋
3
1
2
√
3
2
0
3
∥
√
tan(−𝑎) = − tan(𝑎) cotan(−𝑎) = − cotan(𝑎)
)
− 𝑥 = sin(𝑥)
cos (𝜋 + 𝑥) = − cos(𝑥)
)
− 𝑥 = cos(𝑥)
sin (𝜋 + 𝑥) = − sin (𝑥)
)
− 𝑥 = cotan(𝑥) tan (𝜋 + 𝑥) = tan (𝑥)
𝜋
2
1
2𝜋
3
− 12
√
3
2
√
− 3
tan(𝑎) + tan(𝑏)
1 − tan(𝑎) tan(𝑏)
−1
0
0
cos(𝑎 − 𝑏) = cos(𝑎) cos(𝑏) + sin(𝑎) sin(𝑏)
sin(𝑎 − 𝑏) = sin(𝑎) cos(𝑏) − cos(𝑎) sin(𝑏)
tan(𝑎 − 𝑏) =
tan(𝑎) − tan(𝑏)
1 + tan(𝑎) tan(𝑏)
En particulier on a les relations suivantes avec l’angle double :
cos(2𝑎) = cos2 (𝑎) − sin2 (𝑎) = 2 cos2 (𝑎) − 1 = 1 − 2 sin2 (𝑎)
sin(2𝑎) = 2 sin(𝑎) cos(𝑎)
cos2 (𝑎) =
1 + cos(2𝑎)
2
sin2 (𝑎) =
1 − cos(2𝑎)
2
𝜋)
= − sin(𝑥)
cos 𝑥 +
2
(
𝜋)
sin 𝑥 +
= cos(𝑥)
2
(
𝜋)
tan 𝑥 +
= − cotan(𝑥)
2
(
𝜋
Formules d’addition
cos(𝑎 + 𝑏) = cos(𝑎) cos(𝑏) − sin(𝑎) sin(𝑏)
sin(𝑎 + 𝑏) = sin(𝑎) cos(𝑏) + cos(𝑎) sin(𝑏)
tan(𝑎 + 𝑏) =
1
cos(𝑥)
=
définie si 𝑥 ∕= 0 (𝜋)
tan(𝑥)
sin(𝑥)
1
𝜋
1
si 𝑥 ∕=
(𝜋) 1 + cotan 2 (𝑥) =
si 𝑥 ∕= 0 (𝜋)
2
2
cos (𝑥)
2
sin (𝑥)
sin(−𝑎) = − sin(𝑎)
cos(−𝑎) = cos(𝑎)
cotan(𝑥) =
tan(2𝑎) =
2 tan(𝑎)
1 − tan2 (𝑎)
On dispose également de relations avec la tangente de l’angle moitié.
(𝑎)
1 − 𝑡2
2𝑡
sin(𝑎) =
Si 𝑎 ∕= 𝜋 (2𝜋), on pose 𝑡 = tan
alors cos(𝑎) =
2
1+𝑡
1 + 𝑡2
2
–1/2–
tan(𝑎) =
2𝑡
1 − 𝑡2
Lycée Faidherbe, Lille
PCSI1 - PCSI2
Formulaire de trigonométrie - résumé
Formules de linéarisation :
sin(𝑎) cos(𝑏) =
1
[sin(𝑎 + 𝑏) + sin(𝑎 − 𝑏)]
2
cos(𝑎) cos(𝑏) =
1
[cos(𝑎 + 𝑏) + cos(𝑎 − 𝑏)]
2
1
sin(𝑎) sin(𝑏) = − [cos(𝑎 + 𝑏) − cos(𝑎 − 𝑏)]
2
)
(
)
(
𝑝−𝑞
𝑝+𝑞
cos
sin(𝑝) + sin(𝑞) = 2 sin
2
2
(
)
(
)
𝑝+𝑞
𝑝−𝑞
sin(𝑝) − sin(𝑞) = 2 cos
sin
2
2
(
)
(
)
𝑝+𝑞
𝑝−𝑞
cos(𝑝) + cos(𝑞) = 2 cos
cos
2
2
(
)
(
)
𝑝+𝑞
𝑝−𝑞
cos(𝑝) − cos(𝑞) = −2 sin
sin
2
2
Equations trigonométriques
{
𝑎 = 𝑏 (2𝜋)
cos(𝑎) = cos(𝑏) ⇔
𝑎 = −𝑏 (2𝜋)
{
𝑎 = 𝑏 (2𝜋)
sin(𝑎) = sin(𝑏) ⇔
𝑎 = 𝜋 − 𝑏 (2𝜋)
tan(𝑎) = tan(𝑏) ⇔ 𝑎 = 𝑏 (𝜋)
Lien avec l’exponentielle complexe
𝑒𝑖𝑥 = cos(𝑥) + 𝑖 sin(𝑥)
cos(𝑥) = Re(𝑒𝑖𝑥 ) =
)
𝑎 − 𝑏 𝑖( 𝑎+𝑏
)
𝑒 + 𝑒 = 2 cos
𝑒 2
2
(
)
𝑎 − 𝑏 𝑖( 𝑎+𝑏
)
𝑖𝑎
𝑖𝑏
𝑒 − 𝑒 = 2𝑖 sin
𝑒 2
2
𝑖𝑎
𝑖𝑏
(
1 𝑖𝑥
(𝑒 + 𝑒−𝑖𝑥 )
2
sin(𝑥) = Im(𝑒𝑖𝑥 ) =
1 𝑖𝑥
(𝑒 − 𝑒−𝑖𝑥 )
2𝑖
( ) 𝜃
𝜃 𝑖( 2 )
1 + 𝑒 = 2 cos
𝑒
2
( ) 𝜃
𝜃 𝑖( 2 )
𝑖𝜃
1 − 𝑒 = −2𝑖 sin
𝑒
2
𝑖𝜃
–2/2–
Lycée Faidherbe, Lille