Derivada de una función implicita

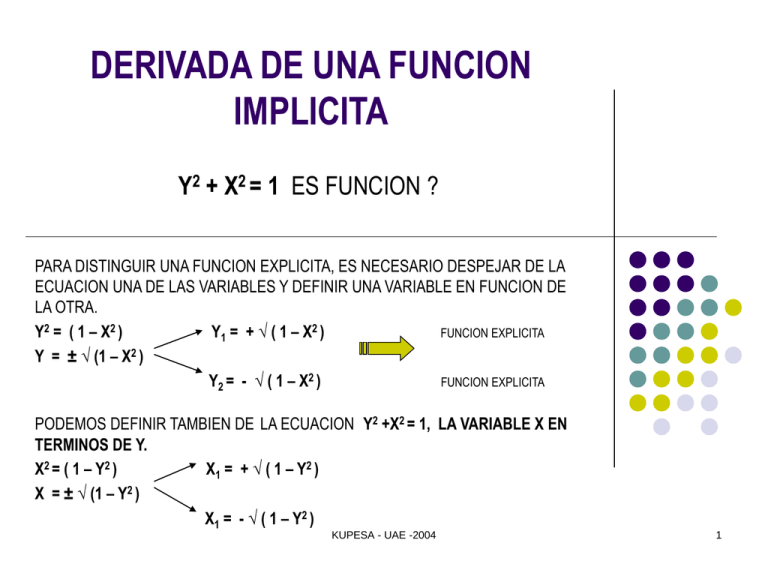
DERIVADA DE UNA FUNCION
IMPLICITA
Y2 + X2 = 1 ES FUNCION ?
PARA DISTINGUIR UNA FUNCION EXPLICITA, ES NECESARIO DESPEJAR DE LA
ECUACION UNA DE LAS VARIABLES Y DEFINIR UNA VARIABLE EN FUNCION DE
LA OTRA.
Y2 = ( 1 – X2 )
Y1 = + √ ( 1 – X2 )
FUNCION EXPLICITA
Y = ± √ (1 – X2 )
Y2 = - √ ( 1 – X2 )
FUNCION EXPLICITA
PODEMOS DEFINIR TAMBIEN DE LA ECUACION Y2 +X2 = 1, LA VARIABLE X EN
TERMINOS DE Y.
X2 = ( 1 – Y2 )
X 1 = + √ ( 1 – Y2 )
X = ± √ (1 – Y2 )
X1 = - √ ( 1 – Y2 )
KUPESA - UAE -2004
1
EJEMPLOS:

x3 + y3 = 6xy
HOJA DE DESCARTES
Cómo podremos derivar
esta función??



Para poder derivarla es necesario que se
defina la variable de trabajo en términos de
la otra. ( ver pagina 71 del libro)


RECORDAR LA DERIVADA FUNCIONAL

Al definir y en términos de x
x3 + y3 (x)= 6xy(x)
Y‘(X) = F‘(X) = DF(x) = dy / dx
:
lo que significa que y(x) es una función implícita con respecto a x
KUPESA - UAE -2004
2
De lo anterior podemos concluir que F esta definida implícitamente por una ecuación si y
solo si, al sustituir Y por F(x)= Y(x) se llega a una identidad y que Y(x) puede ser una de las
muchas funciones definidas en el dominio de la función implícita.

Ejercicios .
Derivar implícitamente las siguientes funciones, ASUMIENDO
a) Y en términos de X : X‘( y ) ??
b) X en términos de Y : Y‘( x ) ??
y2 + x2 = 9

Y4 – x2y + Ln (xy) = 1/5

X3 + y3 = 6xy
SOLUCION:


y2 + x2 = 9
y2(x) + x2 = 9
se define “y” en función de “x” para poder
derivarla como una suma de funciones
explicitas.
2y(x) y‘(x) + 2x = 0
y‘(x) = - 2x / 2y(x)
y‘(x) = -x / y(x)
KUPESA - UAE -2004
3
CONCLUSION:
Si Y‘(X) = F‘(X) = DF(x) = (dF(x) / dx ) = ( dy / dx)
F'(X)


=
dF(x)
dx
DERIVADA FUNCIONAL
F'(x) dx = dF(x)
DIFERENCIALFUNCIONAL
POR EJEMPLO, PARA LA FUNCION Y4 – x2y + Ln (xy) = 1/5, UTILIZANDO NOMENCLATURA
DEL DIFERENCIAL, DETERMINAR EL dy / dx.
y4 – x2y + Ln (xy) = 1/5
4y3 dy – ( 2xydx + x2dy ) +[(ydx + xdy) / xy ] = 0
4y3 dy – x2dy +[ xdy / xy ] = 2xydx – ( ydx / xy )
[4y3 – x2 + x / xy ] dy = [ 2xy – ( y/ xy ) ] dx
dy
dx
=
[ 2xy – ( y/ xy ) ]
[4y3 – x2 + x / xy ]
=
[ 2xy – ( 1 / x ) ]
[4y3 – x2 + 1 / y ]
KUPESA - UAE -2004
4
ANTIDERIVADA o ANTIDIFERENCIAL FUNCIONAL

UNA ECUACION QUE COMPRENDE LAS DERIVADAS DE UNA FUNCION SE LLAMA , ECUACION
DIFERENCIAL.

EL ANTIDIFERENCIAL O ANTIDERIVADA FUNCIONAL ES LA OPERACIÓN CONTRARIA A
DERIVAR.
SI RECORDAMOS EL CONCEPTO DE LA DERIVADA FUNCIONAL :

dF( x ) = F‘(x) = df(x) / dx
dF( x ) = F‘(x) dx = df(x)

PARA IDENTIFICAR LA OPERACION CONTRARIO A DERIVAR, SE UTILIZA UN OPERADOR
LLAMADO OPERADOR DEL ANTIDIFERENCIAL QUE EXPRESA COMO EL PRODUCTO DE
SU DERIVADA POR LA DIFERENCIAL VARIABLE DE DEFINICION :
∫dF
(x)
∫
∫
= F‘(x) dx = f(x) dx = F(x) + C
KUPESA - UAE -2004
5
INTEGRAL INDEFINIDA

LA COLECCIÓN DE TODAS LAS FUNCIONES PRIMITIVAS DE LA FUNCION f(x) , ES
CONOCIDA COMO LA INTEGRAL INDEFINIDA DE f CON RESPECTO DE “x” ,
DENOTANDOLA CON EL OPERADOR DE LA ANTIDIFERENCIAL O ANTIDERIVADA.

ES DECIR, UNA SOLA FUNCION TIENE MUCHAS PRIMITIVAS MIENTRAS QUE UNA
FUNCION SOLO PUEDE TENER UNA DERIVADA.


“ SI F(x) ES UNA PRIMITIVA DE f(x) EN EL INTERVALO I, ENTONCES TODA PRIMITIVA DE f(x)
EN EL INTERVALO ES DE LA FORMA F(x) + C , DONDE C ES UNA CONSTANTE
ARBITRARIA “.
POR EJEMPLO SI CONSIDERAMOS LA FUNCION :
F(x) = X 3
G(x) = X 3 - 5
J(x) = X 3 + 1/2
f(x)= F‘(x) = 3x2
g(x)= G‘(x) = 3x2
j(x)= J‘(x) = 3x2
KUPESA - UAE -2004
F(X) + C
FUNCION PRIMITIVA
6
EJEMPLOS:

DETERMINAR LA INTEGRAL INDEFINIDA DE LAS SIGUIENTES FUNCIONES:
a.
F(x) = 2x
b.
d.
F(x) = 2x + 5
F(x) = x 2
F(x) = x n
e.
F(x) =Cos (x)
c.
∫dF
(x)
=
∫ F‘
(x) dx
=
∫f
(x) dx
= F(x) + C
∫dF( x ) = ∫ F‘(x) dx = ∫ f(x) dx = F(x) + C
KUPESA - UAE -2004
7
TECNICAS DE INTEGRACION












TEOREMAS Y/O PROPIEDADES DE LA ANTIDERIVADA:
∫dF( x )
∫dF( x )
∫dF( x )
∫dF( x )
∫ F‘(x) dx = ∫ f(x) dx = F(x) + C
= ∫ ( g(x) ± j(x) ) dx = ∫ g(x) dx ± ∫ j(x) dx
= ∫ Kf(x) dx = K ∫ f(x) dx
= ∫ xn dx = [ x n + 1 / (n + 1) ] + C
=
METODO DE INTEGRACION POR GENERACION DE SIGNO Y/O CONSTANTE
METODO DE INTEGRACION POR INDUCCION
METODO DE INTEGRACION POR CAMBIO DE VARIABLE
METODO DE INTEGRACION POR PARTES ( ILATE )
METODO DE INTEGRACION POR FRACCIONES PARCIALES
METODO DE INTEGRACION POR SUSTITUCION TRIGONOMETRICA
METODO DE INTEGRACION POR TABLAS Y/O PROG DIGITALES A.C.
( SOFTWARE )
KUPESA - UAE -2004
8
TEOREMA FUNDAMENTAL DEL CALCULO INTEGRAL:
(ver pagina 86 de texto de MAT II )

SI m tg = F'( x ) = LimΔx→0 [ Δy / Δx ]
F'( x ) Δx = LimΔx→0 ( Δy) = Δy
F'( x ) dx = dy
∫f
(x)
∫
dx = dy =
x=b
y(x)
= F(x )
∴
F'(x)= f (x)
x=b
∫f (x) dx = [ f( x )]
x=a
x=a
x=b
∫f (x) dx = ( f( b) – f(a) )
x=a
KUPESA - UAE -2004
9
INTEGRAL DEFINIDA Ξ AREA
x
xb
 ( Sen
x ) dx 
 Cos x 
xa

(  Cos (  )  (  Cos ( 0 ) )  2
x0
Este es el valor del integral definido, que se obtiene al evaluar el TFC.
De lo anterior podemos definir que :
INDEFINIDA
F(X) + C
INTEGRAL
DEFINIDA
F(b) – F(a) == # REAL
- 0 +
AREA > 0
VL SIEMPRE +
KUPESA - UAE -2004
10
AREAS BAJO LA CURVA
LIMITANTE IZQ.
LIMITANTE
DERECHA .
F(x) : FUNCION DE TRABAJO
h
b
X
KUPESA - UAE -2004
11