Derivada de funciones

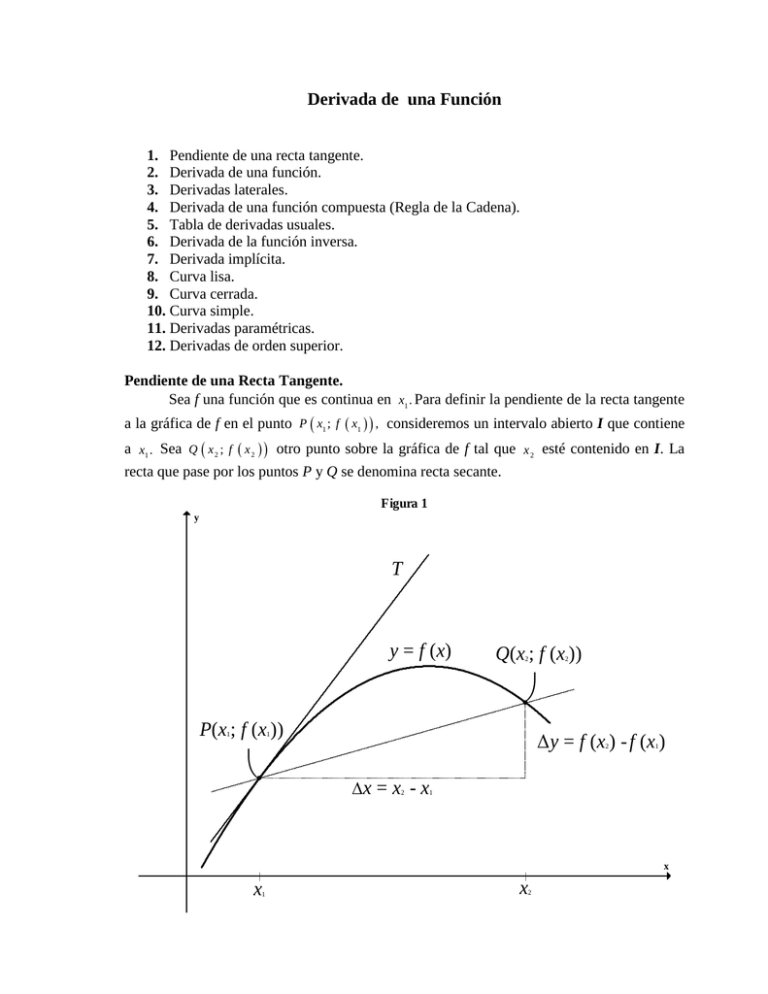
Derivada de una Función
1. Pendiente de una recta tangente.
2. Derivada de una función.
3. Derivadas laterales.
4. Derivada de una función compuesta (Regla de la Cadena).
5. Tabla de derivadas usuales.
6. Derivada de la función inversa.
7. Derivada implícita.
8. Curva lisa.
9. Curva cerrada.
10. Curva simple.
11. Derivadas paramétricas.
12. Derivadas de orden superior.
Pendiente de una Recta Tangente.
Sea f una función que es continua en x1 . Para definir la pendiente de la recta tangente
a la gráfica de f en el punto P  x1 ; f  x1   , consideremos un intervalo abierto I que contiene
a x1 . Sea Q  x 2 ; f  x 2   otro punto sobre la gráfica de f tal que x 2 esté contenido en I. La
recta que pase por los puntos P y Q se denomina recta secante.
Figura 1
y
T
y = f (x)
Q(x ; f (x ))
2
2

P(x ; f (x ))
1
Δy = f (x ) - f (x )
1
2

x = x - x
2
1
1
x


x
1
x
2
Lic. Eleazar J. García
Observe que  x es el cambio del valor x de x1 a x 2 , llamado incremento de x, y
es el cambio del valor de y  f  x  de f  x1  a f  x 2  , llamado incremento de y.
La pendiente de la recta que pasa por los puntos P y Q de la curva de la figura 3.1,
está determinada por:
y
m PQ 
f  x 2   f  x1 
x
Como x 2  x1   x , la pendiente puede escribirse así:
m PQ 
f  x1   x   f  x1 
x
Consideremos ahora el punto P como un punto fijo, y que el punto Q se mueve a lo
largo de la curva hacia P. Esto es igual a decir que  x tiende a cero. Si esto sucede la recta
secante gira sobre el punto P hasta convertirse en una recta tangente a la curva en el punto P,
por lo tanto, la pendiente de la recta tangente en dicho punto puede ser calculada mediante la
siguiente ecuación:
f
m  x1   lím
 x1   x   f  x1 
A 
x
x  0
“La notación m  x1  nos indica que la pendiente que calculemos con la ecuación (A) es la de
la recta tangente a la gráfica de la función y  f  x  en el punto  x1 , f  x1   ”.
Ejercicios resueltos 1.
1.1) Calcule la pendiente de la recta tangente a la parábola f  x   3 x 2  4 en el punto  3;1  .
Solución:
Es evidente que x1  3, por lo tanto, aplicando la ecuación (A) tenemos:
f 3  x   f 3
m  3   lím
x
x  0
 lím
 3  3   x  2  4   31


x
x  0
27  18  x  3   x   27
 lím
x
x  0
 lím
x  0
18  x  3   x 
2
x  0
 lím
x

3 9  6x   x 
2
  27
x
2
 lím 18  3  x   18
x  0
Luego, la pendiente exigida es: m  1 8 .
1.2)
Determine la pendiente de la recta tangente a la curva f  x   sen x en el punto
 12  ,1  .
Solución:
Apliquemos la ecuación (A), con x1  12  :
m  12 

lím
x  0
sen  12    x   sen  12 
x

Derivada de Funciones
sen  12   cos   x   sen   x  cos  12    sen  12 
 lím
 lím
  cos   x   1   sen   x  cos  12  
sen  12 
x
x  0
 lím
sen  12 
  cos   x   1 
x
x  0
  sen  12 
 lím
x 0
 lím
sen   x  cos  12 
1  cos   x 
x
lím
x  0
x
 x 
 cos  12 
 lím
x  0
 lím
x 0
 x 
sen   x 
x
2
x
 lím
x  0
x
2

0
0
sen   x 
y
2
2
2

x
x  0
Ahora, cuando  x  0, 1  cos   x 
1  cos   x 

x
x  0
y
2
lím
sen   x 
x  0
x
 x , entonces,
 lím
x 0
x
x
 lím 1  1, por
x 0
consiguiente:
m  12 

 sen  12 
 cos  12 
 lím
x 0
1  cos   x 
x
 cos  12 
 lím
x 0
sen   x 
x
  sen  12    0  cos  12    1
  0.
Por lo tanto, la pendiente buscada es: m  0 .
Derivada de una Función.
La derivada de una función f, es una función denotada por f , tal que para cualquier
x del dominio de f está dada por:
f   x   lím
x  0
f
 x  x   f  x 
x
B
si este límite existe.
Si x1 es un número del dominio de f, entonces:
f   x1   lím
x  0
f  x1   x   f  x1 
x
C 
si este límite existe.
El proceso de calcular la derivada de una función se denomina derivación o
diferenciación, es decir, la derivación o diferenciación es el proceso mediante el cual se
Lic. Eleazar J. García
obtiene f  a partir de f. Si una función tiene derivada en todo su dominio, se dice que es una
función diferenciable.
Ejercicios resueltos 2.
2.1) Determine la derivada de f  x   x 3 , aplicando la ecuación (B).
Solución:
 x  x   f  x 
f
f   x   lím
x
x  0

 lím
x  3x
3
2
 lím
x  0
 x   3x  x 
x

x
2

x  3x
3
x  3x
 lím
x


2
2
x  3x
3
2
 x 
3
3
 x 
x  3x
3
2
 x 
2
3
x
x
3

x  3x
3
 x   3x  x 


 3x  x    x  
x
  x
3
2

2
2
3
  x   x
3
2

3
3
3
x
3
2
3

x


2
 3x  x    x  
2
3
 3x  x    x  
3x  3x  x    x 
 lím

x
2
2
x  0
  x  
 x   3x  x 
2
3
x
x  3x
 x   3x  x 
3
3
x  0
 lím
x  0
x  0
x  3x
 x  x 
3
3x
2
2 x
3
P or lo tanto,
f  x 
3x
2
2 x
3
2.2) Determine la derivada de la función g  x   x 3 .
Solución:
Apliquemos la ecuación (B),
g   x   lím
x  0
g  x  x   g  x 
x
 lím
x  0
 x  x 
x
3
x
3
2
2
 x   3x  x 
  x  
3
x
3

2
 x  
3
x
3

Derivada de Funciones
x  3x
3
 lím
2
 x   3x  x 
3
3
 lím

3x
2
 x   3x  x 
x 3x  3x  x    x 
2


 lím 3 x  3 x   x     x 
x
x  0
 x 
2
3
x
x 0
2
x 0
 3x
  x   x
x
x 0
 lím
2
2
2
  3x
2
 3x  0  0
2
E n conclusión,
g  x   3x
2
2.3) Determine la derivada de la función h  x   tg x .
Solución.
Aplicando la ecuación (B), tenemos,
h   x   lím
h  x  x   h  x 
x
x 0
1  tg x  tg   x 
x
 tg x
tg x  tg   x   tg x  tg x  tg   x 
2
 lím
x
x 0
tg  x   x  - tg x
x 0
tg x  tg   x 
 lím
 lím
x
x  0
1  tg x  tg   x 
2
 lím
x
x 0
  1  tg x  lím
2
tg   x 
x
x 0
 1  tg x   1  sec x
2
2
P or consiguiente :
h   x   sec x
2
d
Otras notaciones para la derivada de una función f son:
dx
 f
 x   y
D x  f
 x   .
E jercicios propu estos A .
D eterm ine la derivada de cada una de las siguientes funciones :
1) f
x
5) f
x 3
9) f
x 
8 x
Teorema 1.
x
x
2
2) f
x 7x  5
6) f
x
10) f
x 
4
2x  5
cos x
3) f
7) f
11) f
 x  3  4x  2x2
 x   3x 
 x  5x
3
6
x
8) f
2
 x 2
2
4) f
 x   x3  2x
 x   3x3  2x2  6x  1
12) f
x 
cos x  sen x
2
2
Lic. Eleazar J. García
Si una función f es diferenciable en un punto x1 , entonces, f es continua en x1 .
Una función f puede no ser diferenciable en c por alguna de las siguientes razones:
1.
La función es discontinua en c. (Ver figura 2)
2.
La función es continua en c , pero la gráfica de f tiene una recta tangente vertical
en el punto donde x  c. (Ver figura 3)
3.
La función f es continua en c , pero la gráfica de f no tiene recta tangente en el
punto donde x  c. (Ver figura 4). La continuidad no implica diferenciabilidad.
Figura 2
Figura 3
y
y
(c; f (c))
(c; f (c))
x
x
Figura 4
Figura 5
y
Y
(c; f (c))
T2
T1
(a; f (a))
x
T3
T4
(b; f (b))
X
La figura 5 muestra la gráfica de una función que no es diferenciable en los puntos donde
x  a y x  b . La gráfica está compuesta por tres curvas. En el punto ( a ; f ( a )) se han
Derivada de Funciones
trazado las siguientes rectas: T1 tangente a la curva de la izquierda y T2 tangente a la curva
central, las cuales evidentemente tienen pendientes diferentes. Igualmente se han trazado en
el punto ( b ; f ( b )) las rectas tangentes T3 y T4 que igualmente tienen diferentes pendientes.
Esta experiencia nos conduce a pensar en derivadas laterales, lo que estudiaremos a
continuación.
Derivadas Laterales.
i) Si f es una función definida en x1 , entonces, la derivada por la derecha de f en
x1 , denotada por f   x1  , está definida por:
f   x1   lím 
f  x1   x   f  x1 
x
x  0
f   x1   lím 

f  x   f  x1 
x  x1
x  x1
si el límite existe.
ii) Si f es una función definida en x1 , entonces, la derivada por la izquierda de f en
x1 , denotada por f   x1  , está definida por:
f   x1   lím 
f  x1   x   f  x1 
x
x  0
f   x1   lím 

f  x   f  x1 
x  x1
x  x1
si el límite existe.
Ejercicios resueltos 3.
3.1) Determine si la función f es diferenciable en x1 .
x  2
f x 
 x  6
si
x4
si
 4 x
x1   4
Solución.
Puesto que f está definida por trozos, se calculan las derivadas laterales en  4 .
f    4   lím 
x  4
f    4   lím 
x  4
f  x   f  4 
x   4 
f  x   f  4 
x   4 
 lím 
x  4
 lím 
x  4
 x  2    2 
x4
 lím 
  x  6    2 
x4
x  4
x4
x4
 lím 
  lím  1   1
x  4
Como f    4   f    4  , entonces, f no es diferenciable en  4 .
x  4
 lím  1  1
x  4
x  4
x4
  lím 
x  4
x4
x4
Lic. Eleazar J. García
3.2) Decida si la función g  x   2 x  4 es diferenciable en 2.
Solución.
2 x  4
si
x2
4  2 x
si
x2
Puesto que: 2 x  4  
g  x  x   g  x 
g   2   lím 
x
x 0
 lím 
x 0
g  x  x   g  x 
x
x 0
2  x 
x
x 0
x
x 0
 lím 
x
 lím   2   2
 2  x  x   4    2 x  4 
 lím 
2 x  2  x   4  2 x  4
x 0
x
 lím 
x
g   2   lím 
 4  2  x  x    4  2 x 
x 0
4  2 x  2  x   4  2 x
x 0
 lím 
 lím 
, entonces,
x 0
2  x 
x
 lím  2  2
x 0
Ahora, siendo g   2   g   2  , entonces, g no es diferenciable en 2.
3.3)
Determine si la función h  x   co s x es diferenciable en 13  .
Solución.
h 

1
3
   lím
x 0
cos  13    x   cos 13 
x

 lím 
cos 13   cos   x   sen 13   sen   x   cos 13 
x
x  0
 lím 
cos 13   cos   x   1   sen 13   sen   x 
x
x  0
  cos 13  lím 
x  0
1  cos   x 
x
Ahora, cuando  x  0  , 1  cos   x 
 sen 13  lím 
x 0
 x 
2
sen   x 
x
2
y
sen   x 
 x , entonces,
Derivada de Funciones
lím 
 x 
1  cos   x 
 lím 
x
x  0
x  0
2
2
x
 lím 
x  0
x

2
0
0
y
lím 
sen   x 
x
x  0
2
 lím 
x  0
x
x
 lím  1  1,
x  0
luego,
h 
 13   
 cos 13  lím 
1  cos   x 
x
x  0

1
3
   lím
x 0
3
x

cos 13   cos   x   sen 13   sen   x   cos 13 
x
x  0
cos 13   cos   x   1   sen 13   sen   x 
x
x  0
  cos 13  lím 
1  cos   x 
Cuando  x  0 , 1  cos   x 

lím 
x
x  0
 x 
 lím 
x  0
 x 
sen   x 
 sen 13  lím 
x
x  0
1  cos   x 
2
cos  13    x   cos 13 
 lím 
 lím 
x
x 0
  cos 13   0  sen 13   1   sen 13   
h 
sen   x 
 sen 13  lím 
x
x 0
2
y
2
sen   x 
 x , entonces,
2
2
x
 lím 
x  0
x
2

0
0
y
lím 
x  0
2
sen   x 
x
luego,
h 
 13   
 cos 13  lím 
x  0
1  cos   x 
x
sen   x 
 sen 13  lím 
x
x 0
  cos 13   0  sen 13   1   sen 13   
3
2
Puesto que, h   13    h   13   , entonces, h es diferenciable en 13  .
 lím 
x  0
x
x
 lím  1  1,
x  0
Lic. Eleazar J. García
E jercicio s p ro p u esto s B .
D eterm in e si la fu n ció n d ad a es d iferen c iab le en x1 .
1) f
3  2 x
x 
3 x  7

 1 x
3) f  x   
2

 1  x 
5) f
 x 1
si
x2
si
2 x
si
x 1
si
1 x
x2
x1   2
2

x  4
x

  

 x2
x1  2
2) f
x1  1
3

 x
4) f  x    2
 x 3

2
6) f
x
3
x 1
x1   1
si
x2
si
2 x
si
x 0
si
0 x
7) f
x
x1  2
x1  0
x
x1  0
El proceso del cálculo de la derivada de una función aplicando la fórmula (B) es muy
largo y laborioso, por lo tanto, a continuación se proporcionan algunos teoremas que
permiten determinar las derivadas con mayor facilidad; con la finalidad de familiarizarnos
con las notaciones, la derivada se expresará con alguna de las tres expresiones equivalentes
f   x  , D x  f
 x   ,
dy
dx
ó
d
dx
 f
 x   .
Teorema 2. Derivada de una función constante.
Si f  x   c , donde c es una constante, entonces:
f  x  0
Ejemplo.
Si f  x   6, entonces, f   x   0 .
Teorema 3. Derivada de una función potencial.
Si f  x   x n , donde n es un número racional, entonces:
Dx  x
n
  nx
n 1
Ejemplo.
6
Si f  x   x , entonces, f   x   6 x 5 .
Teorema 4. Derivada del producto de una función por una constante.
Si g es una función definida por g  x   c  f  x  , donde f es una función y c una
constante, entonces:
g x  c  f  x
Ejemplo.
8
Si f  x   4 x , entonces, D x  4 x 8   4  D x  x 8   4  8 x 7  32 x 7 .
Derivada de Funciones
A partir del resultado obtenido en el ejemplo anterior, podemos enunciar el siguiente
teorema.
Teorema 5. Derivada del producto de una función potencial por una constante.
n
Si f  x   c  x , donde n es un número entero positivo y c una constante, entonces:
Dx c  x
n
cD x  cn x
n
n 1
x
Teorema 6. Derivada de una adición de funciones.
Si f1 , f 2 , f 3 , f 4 , , f n son funciones y si f es una función definida por:
f
x
f1  x   f 2  x  
 f n  x  y si f 1 x  , f 2  x  , f 3  x  , f 4,
f   x   f1 x   f 2  x   f 3  x   f 4  x  
, f n  x 
existen, entonces:
f n  x 
Ejemplo.
Determine f   x  si f  x   4 x 4  3 x 3  x  5 .
4
3
4
3
f   x   D x  4 x  3 x  x  5   D x  4 x   D x  3 x   D x  x   D x  5 
 4  Dx  x
4
  3 D  x   D  x   D 5  4  4 x
3
x
x
x
3 1
 3  3x
3 1
x
1 1
0
 16 x  9 x  1
3
2
Teorema 7. Derivada de un producto de funciones.
Si f y g son funciones y h una función definida por h  x   f  x   g  x  , y si f   x  y
g   x  existen, entonces:
d
dx
 h  x   
d
dx
 f
 x   g  x    f  x  
d
dx
 g  x    g  x  
d
dx
 f
 x  
Ejemplo.
Sea h  x    2 x 3  2   x 2  x  , determine h   x  .
Apliquemos el teorema 7:
h   x    2 x  2   D x  x  x    x  x   D x  2 x  2    2 x  2   2 x  1   x  x   6 x
3
2
2
3
3
2
2

 4 x  2 x  4 x  2  6 x  6 x  10 x  8 x  4 x  2
4
3
4
3
4
3
Teorema 8. Derivada de un cociente de funciones.
Si f y g son funciones y h una función definida por h  x  
si f   x  y g   x  existen, entonces:
x
, donde
g x
f
g x 0 y
Lic. Eleazar J. García
 f  x   g  x   D x  f
Dx 

 g x 
 x    f  x   D x
 g  x  
 g  x  
2
Ejemplo.
 3x2 
Calcule D x 
.
 x3
Debemos aplicar el teorema 8:
2
 3 x 2   x  3   D x  3 x   3 x  D x  x  3   x  3   6 x   3 x 1 6 x 2  1 8 x  3 x 2
Dx 




2
2
2
 x  3
 x  3
 x  3
 x3
2
2
3 x  18 x
2

 x  3
2
E jercicios propu estos C .
C alcule la derivada de las funciones dad as :
1) f
x
x
3
3

3
x
3
2) f
2
5) D x   2 x  5   4 x  1  


2
d  x  2x  1
8)
 2

dx  x  2 x  1 
9)
 x    2 x 4  1  5 x 3  6 x 
3) f
x
2x  1
3x  4
10)
d
6x
dx
7
 x   x 10  7 x 5
 x3  1  2 2

7) Dx  2
 x  1
x

x 3
3
2
4
2
6) D x   13 x  4 x  5   3 x  x  


2
d 
3
7  3x  


dx 
4) f
 3 x  13 x
4

3
11)
d  4  3x 


5
dx  5 x 
Para determinar la derivada de una función compuesta, se aplica uno de los teoremas
más importantes del Cálculo llamado “Regla de la Cadena”.
Teorema 9. Derivada de una función compuesta (Regla de la Cadena).
Si g es una función diferenciable en x y la función h es diferenciable en g  x  ,
entonces, la función compuesta f  x    h g   x  es diferenciable en x, y su derivada es:
f  x  h
g   x   h   g  x   g   x 
Ejemplo.
Sean f  x   x 3 y g  x   3 x 2  4 x  9. Determinar  f
La función f
g está definida por
f
g  .
g   x   f  g  x   3x  4 x  9  .
2
3
Derivada de Funciones
Para aplicar la regla de la cadena necesitamos calcular f   g  x   y g   x  . Como
f
 x   x 3 , entonces,
2
f  x   3x ,
y así: f   g  x    3  g  x    3  3 x 2  4 x  9  . Además,
2
2
como g  x   3 x 2  4 x  9, luego, g   x   6 x  4 .
Por lo tanto,  f
2
g   x   f   g  x   g   x   3  3 x  4 x  4 
2
6x  4.
Calcular la derivada de numerosas funciones aplicando la fórmula (B) es muy
laborioso y complicado, por tal razón, a continuación se suministra la siguiente tabla:
Tabla de derivadas usuales.
f
x 
k ................................... f   x   0
f
x 
x ................................... f   x   1
f
x 
n 1
x ................................. f   x   nx
f
x 
 g  x   ........................ f   x   n  g  x  
f
x 
g  x  ........ ................... f   x  
f
x 
ln x ............................... f   x  
f
x 
ln  g  x   ....................... f   x  
f
 x   g  x   h  x  .................
f  x   g  x   h x 
f
 x   g  x   h  x  ...................
f  x  g  xh  x  g  x h x 
f
x 
f
x 
x
x
e ................................. f   x   e
f
x 
e
f
x 
x
x
k ............................... f   x   k  ln k
f
x 
k
f
x 
log b  x  ...................... f   x  
Lic. Eleazar
J. García
n
n
g x
hx
gx
gx
............................ f   x  
n 1
 g  x
g  x
2 g x
1
x
g  x
g x
g  xh  x  g  x h x 
 h  x  
............................. f   x   g   x   e
2
gx
.... ....................... f   x   ln k  g   x   k
gx
log b  e 
x
g   x   log b  e 
f
x 
log b  g  x   .................. f   x  
f
x 
 g  x  
f
x 
 g  x  
f
x 
x
x
x .................................................... f   x   x  ln x  1 
f
 x   sen  g  x   ........................................ f   x  
f
x 
cos  g  x   ....................................... f   x    sen  g  x    g   x 
f
x 
2
tg  g  x   ... ....................................... f   x   sec  g  x    g   x 
f
x 
2
cotg  g  x   ....................................... f   x    csc  g  x    g   x 
f
 x   sec  g  x   ......................................... f   x   sec  g  x    tg  g  x    g   x 
f
x 
csc  g  x   ......... ................................ f   x    csc  g  x    cotg  g  x   . g   x 
f
x 
arcsen  g  x   .................................... f   x  
x 
arccos  g  x   .................................... f   x  
x 
arctg  g  x   .................. .................... f   x  
f
f
h x
gx
g x
.................... f   x   h   x   g  x  
................... f   x   g   x   g  x  
h x
gx
 ln  g  x    h  x   g  x  
h  x  1
 ln  g  x    g   x   g  x  
gx
cos  g  x    g   x 
g  x
1  g  x 
2
 g  x
1  g  x 
g  x
1  g  x 
2
2
 g  x 
Derivada de Funciones
g  x
f
x 
arg tgh ............................................ f   x  
f
x 
arg cotgh  g  x   ............................. f   x  
f
x 
arg sech  g  x   ............................... f   x  
x 
arg csch  g  x   ......... ...................... f   x  
f
1  g  x 
2
 g  x
1  g  x 
2
 g  x
g  x  1  g  x 
2
 g  x
g  x  1  g  x 
2
Ejercicios resueltos 4.
4.1) Calcule la derivada de la función f  x  
3
ln x
2x  1
2
.
Solución.
Debemos aplicar el teorema 8 y la regla de la cadena, así:

 ln 3 x   2 x 2  1    ln 3 x   2 x 2  1 
 ln 3 x 
f  x  
 
2
2
 2x  1
 2 x 2  1
 3 ln x   2 x
2
 3 ln x   ln x   2 x  1    ln x   2 x 
2

2
2x
 3 ln x   2 x  1   2 x
x  2 x  1
2

 1
2
2
2
2
x  2 x  1
2
P or ende,
2
2
ln x  2 x  3  ln x   3 
x  2 x  1
2
2
 1
2x

2
 2 x  ln x 
 1
3
2
6 x ln x  3 ln x  2 x ln x
2

x

2
2
x  2 x  1
2
2
2
f  x 
3
ln x
ln x  6 x  3  2 x ln x 
2

2
2
2
2
3
2
2
2
2
ln x  2 x  3  ln x   3 
x  2 x  1
2
2
3
Lic. Eleazar J. García
Dada la función g  x   8 2 x
4.2)
2
 x5
 co s
3
4x
 3,
5
determine g   x  .
Solución.
Apliquemos la regla de la cadena en cada sumando.
En efecto,
2x
g   x   8

2
 x5
 cos
 2x  x  5
2

4x
3
8

  ln 8   4 x  1  8

  ln 8   4 x  1  8
2

2 x  x5 
   cos 3  4 x 5  3   
 3    8





5
2
2 x  x5
2
2 x  x5
2
2 x  x5
 ln 8   3 cos  4 x
2
   3 cos  4 x
2
  60 x
4
cos
2
5
5
5
 3    cos  4 x  3  




5
5
 3     sen  4 x  3    4 x  3 


4x
5
 3  sen  4 x  3 
5
P or con siguiente,

g   x    ln 8   4 x  1  8
2
2 x  x5

4
cos
2
4x
 3  sen  4 x  3 
5
5
2
x  7 x  12 
.

x4

Derive la función h  x   ln 
4.3)
  60 x


Solución.
Apliquemos la fórmula para derivar el logaritmo neperiano de una función y
resolvamos las derivadas indicadas.
Efectivamente,
 
h   x    ln 
 

2
x  7 x  12  
 

x4





2
x  7 x  12 


x4

x  7 x  12


2
2
 7 x  12 

 x  4   x2
 x  4


2


x  22 x  16
2 x  6 x  32 x  96
3
2
2
 x 2  7 x  12 


x4



x  7 x  12
x4
 7 x  12   x  4  
2
2
x  7 x  12 


x4

2

1
2
x4
x
 x 2  7 x  12 
1

2 
x4


2

2x  7 x  4   x2
 7 x  12  1 
2
 7 x  12 
2  x
2  x  4 

x4


Derivada de Funciones
P or lo tanto,
h x  
4.4)
x  22 x  16
2
2 x  6 x  32 x  96
3
2
Determine la derivada de la función f  x   e 3 x  tg 2 x .
Solución.
Apliquemos el teorema 7 y resolvamos las derivadas señaladas, así,


3x
2
3x 
2
3x
2
3x
2
3x
f   x    e  tg x    e   tg x  e  tg x   3 e  tg x  e  2 tg x  tg x  
 3e
3x
 tg x  2 e
2
3x
 tg x  sec x
2
E n conclusión,
3x
2
3x
2
f   x   3 e  tg x  2 e  tg x  sec x
4.5)
 1  x2  1 
.


x


Calcule la derivada de la función f  x   arctg 
Solución.
Aplicando la fórmula que aparece en tabla de derivadas usuales, tenemos que,


f   x    arctg 




2
1  x  1 
 

x

1

2 2

1

x
  1   x 




x
x  1  x
2
2
1 x 1


x

2

1 



1 x 1


x

2
2

1  x  1  x
2
2
2
x






1 x 1
2
2
1
1

2
1

x
 2 1  x 2   0   x 
2


2 1 x  2
2


x  1  x
2
1  x  1 1
2

2

2

1 x
1 x
2
1 x 1
2

2
Lic. Eleazar J. García
1 x 1
2

2

1 x 1
2

1 x
2


1
2 1 x
2
P or lo tanto,
f  x 
4.6)
1
2 1 x
2
  2 x  3  x2  2 x  3 
 , calcular g .
Dada la función g  x   ln 
4


3x


Solución.
En efecto,

   2 x  3  x2  2 x  3 

    ln  2 x  3   ln  x 2  2 x  3   ln  3 x 4  
g   x    ln 
4



3x
 

 


2
4

  ln  2 x  3     ln  x  2 x  3     ln  3 x  






 2 x  3 
2x  3
2
2x  3

x

 2 x  3
2

x  2x  3
2
2x  2
x  2x  3
2

 3 x 
4

3x

4
2
2x  3

2x  2
x  2x  3
2

12 x
3x
3
4
4
x
3
C onsecuentem ent e,
g  x 
2
2x  3

2x  2
x  2x  3
2

4
x
3
Derivada de la función inversa.
Si la función y  f  x  es diferenciable con respecto de x, entonces, x  f
diferenciable con respecto de y, y se verifica la siguiente relación:
d
 f  x   
d
dx
f
dy 
1
1
 y  
D 
1
 y  es
Derivada de Funciones
Ejercicios resueltos 5.
5.1) Determine la derivada de la función f  x   arcco s x , aplicando la relación (D).
Solución.
Si y  arccos x , entonces, x  cos y , por ende, aplicando la relación (D), tenemos
que,
d
dx
 f
 x  
1

d

 cos y 
dy
1
 sen y
 
1
1  cos y
 
2
1
1 x
2
P or lo tanto,
1
f  x  
5.2)
1 x
2
Sea g  x   tg x , calcule g  usando la relación (D).
Solución.
Puesto que, y  tg x , entonces, x  arctg y , luego, si usamos la relación (D),
obtenemos,
d
 g  x   
d
dx
dy
1
1

 1  y  1  tg x  sec x
2
1
 arctg y 
1 y
2
2
2
P or consiguiente,
g   x   sec x
2
5.3)
Empleando la relación (D), determine la derivada de h  x   ln  3 x  .
Solución.
Como, y  ln  3 x  , entonces, x  13 e y , en consecuencia,
d
 h  x   
d
dx
1

dy
P or ende,
h x  
1
x
1
3
e
y


1
1
3
e
y
3

e
ln  3 x 

3
3x

1
x
Lic. Eleazar J. García
5.4)
Valiéndonos de la relación (D), calcule la derivada de f  x  
Solución.
Siendo y 
d
dx
 f
 x  
2 x  1, entonces, x 

1
d
 12  y 2  1  

dy 

1
1
2
y
2
 1  , así
2 x  1.
que,
1

2x 1
y
E n consecuencia,
f  x 
5.5)
1
2x 1
Dada la función g  x   1 0 sen x , calcule g  utilizando la relación (D).
Solución.
Ya que, g  x   1 0 sen x , entonces, x  arcsen  lo g y  , luego,
d
dx
 g  x   
d
dy

10
1
1

sen x
1   log y 
1   log 10
log e
 ln 10  cos x  10
sen x


 log y 
 arcsen  log y  
1   log y 
log e

2
log e
y
2
2

10
sen x
1  sen x
2

cos x  10
log e
sen x
y 1   log y 
2
sen x
log e
; recuerde que : log b e  ln b  1.
P or lo tanto,
g   x   ln 10  cos x  10
s en x
Derivada implícita.
Existen funciones que no pueden expresarse explícitamente. Por ejemplo, no se
puede resolver la ecuación 2 x 2  4 x  3  y 3  5 y 2  4 para y en términos de x. Pueden existir
una o más funciones y  f  x  tales que 2 x 2  4 x  3   f  x    5  f  x    4; cuando esto
es así, se dice que la función f está definida implícitamente.
Ahora, la derivada de y con respecto a x puede determinarse mediante la
diferenciación implícita.
3
2
Derivada de Funciones
Ejercicios resueltos 6.
6.1) Determinemos
dy
dx
, dada la ecuación 2 x 2  4 x  3  y 3  5 y 2  4.
Solución.
Para calcular la derivada pedida, diferenciemos ambos miembros de la ecuación con
respecto de x y despejemos D x  y  , así:
Dx  2 x  4 x  3  Dx  y  5 y  y 
2
Dx 2 x
2
3
2
  D  4 x   D 3  D  y   D 5 y   D  y 
3
x
x
2
x
x
x
4 x  4  0  3 y D x  y   10 yD x  y   D x  y 
2
2
4 x  4   3 y  10 y  1  D x  y 
2
2
Dx  y  
6.2)
4x  4
2
3 y  10 y  1
2
Sea co s  x  y   y sen x , hallar
dy
.
dx
Solución.
Diferenciemos ambos miembros con respecto de x y despejemos
d
dx
 cos  x  y   
 sen  x  y 
d
dx
x  y

d
dx
dy
 y sen x 
 sen x  y
dx
d
dx
 sen x 
dy
 dx dy 
 sen  x  y  

 sen x
 y cos x

dx
 dx dx 
 sen  x  y   sen  x  y 
dy
 sen x  sen  x  y  
dy
dx
dx
 sen x
dy
 y cos x
dx
  sen  x  y   y cos x
dy
dx
:
Lic. Eleazar J. García
dy

dx
6.3)
 sen  x  y   y cos x
sen x  sen  x  y 
Siendo, y  cos  x  y  , hallar
dy
.
dx
Solución.
Diferenciando ambos miembros con respecto de x y despejando
dy
dx
dy
dx

d
dx
dy
dx
, obtenemos,
 cos  x  y  
  sen  x  y  
d
dx
x  y
 dx dy 
  sen  x  y   


dx
 dx dx 
dy
dy
dx
dy
dx
6.4)
  sen  x  y   1  sen  x  y  
 
dy
dx
sen  x  y 
1  sen  x  y 
Determine
dy
dx
, de la ecuación sen  xy   x .
Solución.
Debemos diferenciar ambos miembros con respecto de x y luego despejemos
d
dx
 sen  xy   
cos  xy  
d
dx
d
dx
 xy   1
dy 
 dx
cos  xy   
y x
1
dx 
 dx
x
dy
dx
.
Derivada de Funciones
y  cos  xy   x  cos  xy  
dy
1
dx
dy

1  y  cos  xy 
dx
x  cos  xy 
E jercicios propu estos D
D eterm ine la derivada de y con respecto a x :
1) x  y  25
2
2) x  y  8 xy
2
3
6) sen x  cos y  9
2
2
3
3
x
3)
7 ) x sen y
2
3
yx y
2
 y cos x  1
2
3
4) y  sen  x y
3
2

5) x y  x  y
8) cotg xy  xy  0
4
6
2
2
9) x y  2 xy
2
5
Supongamos que una partícula se mueve en un plano, de manera tal que sus
coordenadas ( x ; y ), de su posición en cualquier tiempo t, están dadas por las ecuaciones:
x  f  t  y y  g t  .

Para cada número t del dominio común de f y g, la partícula se encuentra en el punto
f  t  ; g  t   , y el conjunto de todos estos puntos describe una curva plana C recorrida por
la partícula. Las ecuaciones x  f  t  y y  g  t  , se llaman ecuaciones paramétricas de C y
la variable t se llama parámetro.
Si eliminamos el parámetro de las ecuaciones paramétricas, se obtiene una ecuación
en x e y, la cual es denominada ecuación cartesiana de C.
A partir de una ecuación cartesiana podemos obtener una ecuación paramétrica, y
viceversa.
Ejemplos.
1) Para determinar unas ecuaciones paramétricas de y  2 x 2 , se procede de la
manera siguiente: puesto que, la variable y está expresada en función de x, hacemos x  t e
y  2 t , por lo tanto, las ecuaciones paramétricas de y  2 x son:
2
2
2
y  2t
y
2) Obtenga la ecuación cartesiana de la curva definida por las ecuaciones
paramétricas
x  5 cos t
y y  5 sen t
Para eliminar el parámetro t, se elevan al cuadrado los dos miembros de cada
ecuación paramétrica y se suman, así:
xt
 x 2  y 2  25 cos 2 t  25 sen 2 t

x   5 cos t  
 2
2
2
2
  x  y  25  cos t  sen t 

2
2
y   5 sen t  
 2
2
 x  y  25
2
2
A continuación se darán tres definiciones de términos relacionados con las curvas
planas, las cuales serán aplicadas posteriormente.
Lic. Eleazar J. García
Curca lisa.
Una curva plana C definida por las ecuaciones paramétricas
x  f t  y y  g t 
atb
se dice que es lisa o suave en el intervalo cerrado  a ; b  si f  y g  son continuas en  a ; b  ,
y además, f   t  y g   t  no son cero simultáneamente en cada t   a ; b  .
Ejemplo.
Sea C la curva definida por las ecuaciones paramétricas
f  t   5 co s t y g  t   5 sen t
0  t  2
Como f   t    5 sen t y g   t   5 co s t son continuas para todo t   0; 2   , y además, no
son cero simultáneamente en cualquier t, entonces la curva C es lisa.
Si un intervalo I puede partirse en un número finito de subintervalos en los que la
curva C es suave, entonces se dice que C es lisa a trozos en I.
Curva cerrada.
Una curva plana C definida por las ecuaciones paramétricas
x  f t  y y  g t 
atb
se dice que es cerrada si el punto inicial A  f  a  ; g  a   coincide con el punto final
B  f b ; g b .
Fig. 3.5
A
B
La figura 3.5 muestra una curva cerrada y lisa donde los puntos A y B coinciden.
Curva simple.
Una curva plana C definida por las ecuaciones paramétricas
x  f t  y y  g t 
atb
se dice que es simple entre los puntos A  f  a  ; g  a   y B  f  b  ; g b   si
es diferente del punto
 a; b  .
 f  t  ; g  t   para todo
2
2
 f t ; g t 
1
1
t1 y t 2 diferentes del intervalo abierto
Derivada de Funciones
“Una curva simple no se cruza a sí misma”.
En la figura 3.5 se muestra una curva cerrada simple lisa.
Derivadas paramétricas.
Supongamos que una curva lisa C está definida paramétricamente por x  f  t  y
y  g t  ,
y que éste par de ecuaciones define al menos una función diferenciable h para la
cual y  h  x  . La derivada de cada función h, denotada por
dy
dt
mediante la siguiente ecuación:
miembro entre
dx
dt
dy
dt

dy
dx
, está relacionada con
dx
dt
y
dy dx
dx

. Si
 0, podemos dividir miembro a
dx dt
dt
para obtener:
dy
dy
 dt .
dx dx
dt
2
Para hallar la derivada
d y
dx

d y
d 


2
dx 
dx


2
dy 
 dy

d  dt
dt


dx  dt  dx


dt 
 dt
2
dx d y

dt dt
2
, a la igualdad anterior la derivamos con respecto a x:
2
2
2
dx d  dy  dy d  dx 
dx d y dy d x







2
2
 dt
1
dt dt  dt  dt dt  dt  dt
dt dt
dt dt



2
2
dx
dx
 dx 
 dx 
 dx




dt

 dt 
 dt 
2

dy d x
dt dt
 dx 


 dt 
2
3
3
Para hallar la derivada
d y
dx
3
2
derivamos
dx
4
manera similar para determinar
d y
2
con respecto a x, y se procede de
5
d y d y
,
, etc.
4
5
dx
dx
Puesto que, las derivadas paramétricas que hemos considerando son funciones
dependientes del parámetro “t”, las siguientes fórmulas son alternativas para hallar las
derivadas paramétricas:
dy
Primera derivada paramétrica:
dy
dx

dt
dx
dt
Lic. Eleazar J. García
2
Segunda derivada paramétrica:
d y
dx
dx
3
4
Cuarta derivada paramétrica:
d y
dx

4
n
n-ésima derivada paramétrica:
d y
dx
d  dy  1
dt  dx  dx
dt
2
d d y 1


2 
dt  dx  dx
dt
3
d y
Tercera derivada paramétrica:

2
n
3
d d y 1

3 
dt  dx  dx
dt
n 1
d d
y 1

.

n 1 
dt  dx
 dx
dt
Ejercicio resuelto 7.
Dadas las ecuaciones paramétricas x  2 t 2  3 y y  t 5  t , determine
2
dy
d y
y
dx
dx
2
.
Solución.
dy
Como
dx
2
d x
 4t ,
dt
dt
dy
 4,
2
dt
2
 5t  1 y
4
d y
dt
2
 20 t , entonces
3
dy
dt 5 t  1

y
dx
4t
4

dx
dt
2
dx d y
2
d y
dx
2

dt dt
2
2

dy d x
dt dt
 dx 


 dt 
3
2

 4 t   20 t 3    5 t 54
 4t 
 1  4 
3
80 t  20 t  4
4

4
64 t
15 t  1
4

3
16 t
Usando la fórmula alternativa tenemos que:
2
d y
dx
2
4
 20 t
d  dy  1
d  5t  1  1





dt  dx  dx
dt  4 t  4 t
dt
3
  4 t    5t
 4t 
2
4
 1  4  1
4t
15 t  1
4

16 t
3
.
3
.
Derivada de Funciones
E jercicios propu estos E
2
dy
D eterm ine las derivadas
d y
y
dx
1) x  a cos t , y  b sen t
4) x 
3 at
1 t
2
,y 
3 at
2
1 t
7 ) x  cos t , y  sen t
2
dx
2
.
2) x  a  t  sen t  , y  a 1  cos t 
3) x  a cos t , y  b sen t
5) x  2 ln  cotg t  , y  tg t  cotg t
6) x  4 sen t , y  4 cos t
8) x  t  2 t , y  5 t  t
5
3
3
3
9) x  2 cos t , y  3 sen t
3
2
2
3.17 Derivada de orden superior.
Si la función f es diferenciable en todo su dominio, entonces su derivada f  se le
llama primera derivada de f o primera función derivada. Si la función f  es también
diferenciable, entonces la derivada f  se denomina segunda derivada de f o segunda
función derivada… Si continuamos derivando n veces, entonces la derivada f 
llamada n- ésima derivada de f. La función f puede representarse como f
0
n
es
.
A continuación conoceremos las distintas notaciones para las derivadas de orden
superior:
Primera derivada: y ¢,
f ¢( x ) ,
dy
d
é f ( x )ù,
û
dx ë
,
dx
2
f ¢¢( x ),
d y
f ¢¢¢( x ),
d y
Segunda derivada: y ¢¢,
dx
2
d
dx
3
2
é f ( x )ù,
û
dx ë
,
f
(4)
( x ),
d y
3
dx
4
d
4
n
n-ésima derivada: y ( n ) ,
f
(n)
( x ),
d y
dx
n
,
3
D x éf ( x )ù
ë
û
4
éf ( x )ù,
û
dx ë
,
2
D x éf ( x )ù
ë
û
3
d
4
Cuarta derivada: y ( 4 ) ,
2
é f ( x )ù,
û
dx ë
,
3
Tercera derivada: y ¢¢¢,
D x é f ( x )ù
ë
û
d
4
D x éf ( x )ù
ë
û
n
é f ( x )ù,
û
dx ë
n
n
D x é f ( x )ù.
ë
û
Para familiarizarnos con la derivación de orden superior, veamos con detenimiento el
desarrollo de los siguientes ejemplos.
Ejercicios resueltos 8.
8.1) Las derivadas f   x  , f   x  , f
(4)
x y
f
(5 )
 x  de
7
4
f  x   5x  2x  3x
son:
Lic. Eleazar J. García
f   x  
d
dx
d
f   x  
f
(4)
f
(5)
d
 f   x   
 5 x 7  2 x 4  3 x   35 x 6  8 x 3  3

dx 
 f   x   
d
 x  

 35 x 6  8 x 3  3   210 x 5  24 x 2

dx
dx 
d
d
 x    f   ´ x     210 x 5  24 x 2   1050 x 4  48 x
dx
dx
d
x 
f
dx 
(4)
d
1050 x 4  48 x   4200 x 3  48.

dx 
8.2) Las derivadas f   x  , f   x  , f   x  y f ( 4 )  x  de f  x   sen 6 x son:
f  x 
f   x  
d
dx
d
dx
f   x  
f
(4)
 f
x 
d
dx
 x  

d
 sen 6 x   6 sen 5 x cos x

dx 
 f   x   
 f   x   
d
dx
d
 6 sen 5 x cos x   30 sen 4 x cos x  6 sen 6 x

dx 
d
 30 sen 4 x cos x  6 sen 6 x   120 sen 3 x cos x  66 sen 5 x

dx 
 f   x   
d
120 sen 3 x cos x  66 sen 5 x   360 sen 2 x cos x  450 sen 4 x .

dx 
Bibliografía
[1] Rabuffetti Hebe T. Introducción al Análisis Matemático, décima edición.
[2] Apostol Tom M. Calculus, segunda edición.