Convertidor SEPIC
Anuncio
TAREA - CONVERTIDOR SEPIC
Fernando
Anatael
Curso: 3º Ingeniería Electrónica Industrial y Automática
Asignatura: Electrónica de Potencia
Profesor: Sergio
El convertidor SEPIC (Single-ended primary-inductor converter) es un tipo de convertidor de
DC-DC que permite que el potencial eléctrico en su salida sea mayor, menor, o igual que el
potencial en su entrada, su salida es controlada por el ciclo de trabajo del transistor de control.
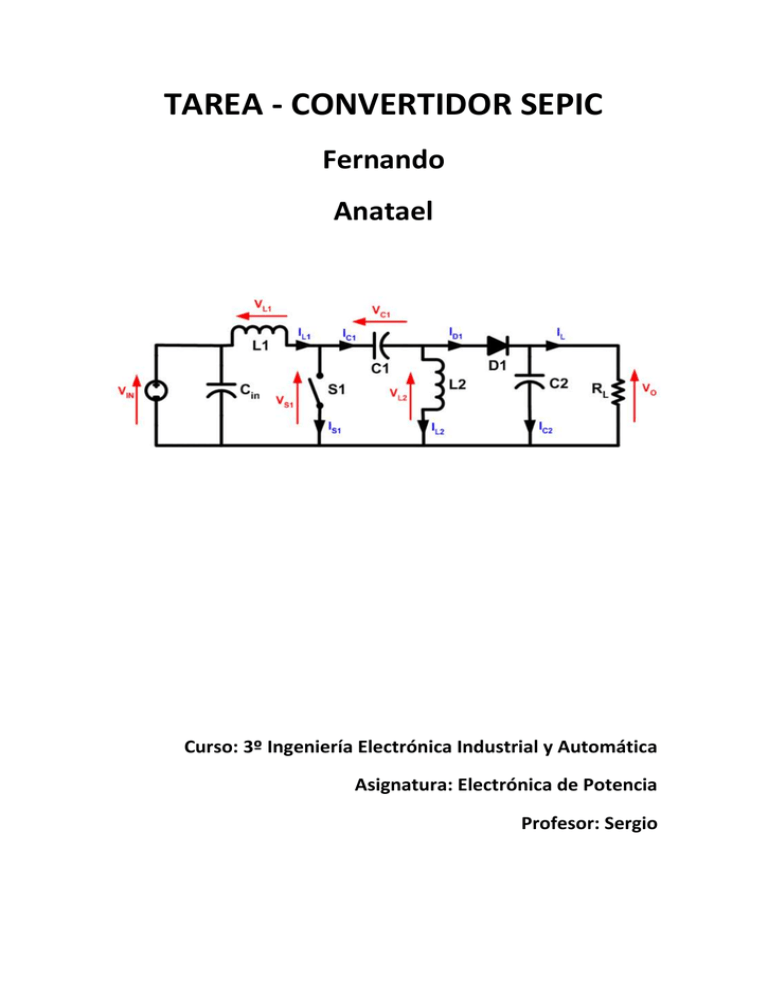
El circuito del SEPIC que analizaremos para este trabajo es el siguiente:
Primero observamos las dos situaciones posibles del circuito:
Cuando el interruptor está cerrado (Ton):
Por el diodo no pasa corriente ya que está polarizado inversamente.
Deducimos las siguientes relaciones:
VL1 = Vi
VL2 = VC1
IL2 = IC1
IC2 = −Io
Cuando el interruptor está abierto (Toff):
Pasa corriente por el diodo pero no por el interruptor
Deducimos las siguientes relaciones:
VL1 = Vi − VC1 − Vo
VL2 = −VC2 = −Vo
IL1 = IC1
IC2 = Ii − IL2 − Io
Cálculos teóricos:
- Primeramente calcularemos la relación de voltajes en modo continuo, esto es la relación
entre el voltaje de salida y el voltaje de entrada. (D es la relación entre TON y T).
Vo = Vi ·
1
1−D
1−D
1
D
− Vo ·
= Vo (1 +
) = Vi ·
=> Vo =
· V =>
1−D
D
D
1−D
1−D i
Vo
D
=
Vi 1 − D
- Ahora calculamos los parámetros IL1 , ΔiL1 , IL2 , ΔiL2 , VC1 , ΔvC1 y ΔvC2 :
Cálculo de IL1 :
Podemos deducir del circuito que la potencia de entrada equivale a la de salida, ya que no
existen pérdidas al tratarse de un circuito ideal. Por ello deducimos:
Pi = Po = Vi · Ii = Vo · Io => Vi IL1 = Vo · Io => IL1 =
Vo ·Io
Vi
=>Suponiendo la relación entre
Vo y Vi finalmente nos queda que:
IL1 =
DIo
(1 − D)
Cálculo de ΔiL1:
ΔiL1 representa la cantidad de rizado de corriente que tenemos en la entrada. Podemos
calcularlo a partir del circuito en su configuración con el interruptor (o MOSFET) cerrado, para
este caso tenemos que la tensión a través de L1 equivale a la tensión de entrada, por ello:
VL1ON = Vi = L1 ·
diL1
∆iL1
= L1 ·
=>
dt
DT
=> ∆iL1 =
Vi DT
L1
=
Vi D
L1 f
Cálculo de IL2 :
Para el circuito con el interruptor abierto tenemos que iL2 = iD − iC1 , donde iD es la corriente
que pasa por el diodo, que a su vez es iD = iC2 + Io . Sabemos que la corriente media en un
condensador es igual a 0, así que tenemos que iD = Io ; por consiguiente IL2 = Io
Cálculo de ∆iL2:
∆iL2 representa el rizado de la corriente en L2, podemos calcularlo a partir del circuito con la
configuración del interruptor abierto, que en su caso la tensión el L2 coincide con la de salida
en sentido opuesto. Si así lo hacemos, deducimos lo siguiente:
VL2OFF = −Vo = L2 ·
diL2
dt
=> ∆iL2 =
∆i
L2
= L2 · (1−D)T
=>
−(1−D)·Vo
L2 f
Cálculo de VC1 :
Cuando el interruptor está cerrado (Sw ON), la tensión de L2 equivale a la de C1, ya que se
encuentran en paralelo. Calcularemos la VC1 a partir de datos conocidos del circuito:
VL2 =
TON
TOFF
TON
TOFF
1
1
VL2ON + ∫
VL2OFF ) = (∫
VC1 − ∫
Vo ) =>
(∫
T 0
T 0
TON
TON
=> VC1 =
(1−D)Vo
D
=
Vo (1−TON )
TON
Cálculo de ∆vC1 :
∆vC1 representa el rizado de voltaje que hay en el condensador C1, para calcularlo nos fijamos
en el caso en el que el interruptor está cerrado (Sw ON). En este caso la intensidad que va por
ambos los componentes C1 y L2 es la misma. Por ello tenemos:
iL2ON = iC1ON = C1 ·
dvC1
dt
T
T
=> ∫0 ON iL2 dt = C1 ∫0 ON vC1 dt => {Mediante el cálculo por
áreas...} => IL2 TON = C1 ∆vC1 => {IL2 = Io , lo hemos deducido antes} =>
∆vC1 =
Io TON Io D
=
C1
C1 f
Cálculo de ∆vC2 :
∆vC2 representa el rizado de voltaje por el condensador C2, para calcularlo nos fijamos en el
circuito con el interruptor cerrado otra vez (Sw ON). La intensidad por C2 coincidirá con la
intensidad por la carga, que se sabe que tiene poco rizado, por lo que podemos aproximar que
io = Io . Si nos fijamos cuando Sw está OFF, la intensidad por C1 coincide con la intensidad por
L1.
iC2 = iL2 − Io
Sabemos que Io = IL2 , por tanto iC2 = iL2 − IL2 .
iC2 = C2 ·
T/2
dvC2
T∆iL2
T∆iL2
=> ∫ iC2 dt = C2 ∆vC2 =>
= C2 ∆vC2 => ∆vC2 =
=>
dt
2
2C2
0
{Sabemos que ∆iL2 =
−(1−D)·Vo
,
L2 f
así que despejamos...} => ∆v𝐶2 =
−𝑇(1−𝐷)𝑉𝑜
2𝐶2 𝐿2 𝑓
- Condición crítica del paso de Modo Continuo a Modo Discontinuo:
Para determinar el límite de funcionamiento en Modo Continuo nos debemos fijar en la
corriente que pasa por el diodo, que sólo conduce cuando el Sw está abierto (durante Toff).
La condición límite para el paso de un modo a otro es que la corriente del diodo caiga a 0 justo
en el instante T. Si se da que la corriente llega a 0 antes de T, el circuito entra en Modo
Discontinuo. En el caso límite se tiene que dar lo siguiente:
𝐼𝐿1𝑀𝐼𝑁 − 𝐼𝐿2𝑀𝐼𝑁 ≥ 0
𝐼𝐿1𝑀𝐼𝑁 = 𝐼𝐿1 −
𝐼𝐿1 −
∆𝑖𝐿1
; 𝐼𝐿2𝑀𝐼𝑁
2
= 𝐼𝐿2 +
∆𝑖𝐿2
2
∆𝑖𝐿1
∆𝑖𝐿2
− 𝐼𝐿2 −
≥0
2
2
Si tenemos en cuenta las ecuaciones calculadas anteriormente, nos queda:
𝐷𝐼𝑜
(1−𝐷)
𝑉𝐷
1𝑓
− 2𝐿𝑖
𝑉 𝐷
2𝑓
− 𝐼𝑜 + 2𝐿𝑖
𝐷
≥ 0 => 𝐼𝑜 (1−𝐷 − 1) +
𝑉𝑖 𝐷 1
(
2𝑓 𝐿2
1
𝐼
𝑜
− 𝐿 ) ≥ 0 => − 1−𝐷
+
1
𝑉𝑖 𝐷
2𝑓
1
1
𝐿2
𝐿1
( − )≥0
La condición para el Modo Continuo será:
−𝐼𝑜 𝐿||1,2 ≥
−𝑉𝑖 𝐷(1 − 𝐷)
2𝑓
En cuanto se deje de cumplir esta relación, el convertidor SEPIC pasará a operar en su Modo
Discontinuo.
Donde 𝐿||1,2 es el equivalente en paralelo de las dos bobinas.
1
1
1
( + )
𝐿1 𝐿2
- Relación de voltajes en Modo Discontinuo:
Los circuitos equivalentes del SEPIC en Modo Discontinuo son tres:
* Uno válido durante 𝑇𝑂𝑁 (cuando Sw está cerrado), otro válido durante 𝑇2 (cuando Sw está
abierto) y otro durante 𝑇3 , (la suma de 𝑇2 y 𝑇3 suponen el nuevo ciclo de OFF) siendo la nueva
configuración del circuito la siguiente:
De este circuito deducimos las nuevas relaciones:
𝑉𝐿1 = 𝑉𝑖 − 𝑉𝐶1 − 𝑉𝑜
𝑉𝐿2 = 𝑉𝐶1
𝑖𝐿1 = 𝑖𝐶1 = 𝑖𝐿2 ≡ 𝑖1
𝑖𝐶2 = 𝑖𝑜 ≡ 𝑖2
Para deducir la relación de voltajes, calculamos el valor medio del voltaje que pasa por las
bobinas:
< 𝑉𝐿 > = 0 =>
1 𝑇𝑂𝑁
1 𝑇2 +𝑇3
∫ 𝑉𝐿1𝑂𝑁 𝑑𝑡 + ∫
𝑉𝐿1𝑂𝐹𝐹 𝑑𝑡
𝑇 0
𝑇 0
Despejamos para el caso particular de la bobina L1, el valor medio del voltaje en la bobina
también será 0:
< 𝑉𝐿1 > =
< 𝑉𝐿1 > =
𝑇𝑂𝑁
𝑉𝑖
𝑇
1 𝑇𝑂𝑁
1 𝑇2 +𝑇3
∫ 𝑉𝑖 𝑑𝑡 + ∫
(𝑉𝑖 − 𝑉𝐶1 − 𝑉0 + 𝑉𝑖 − 𝑉𝐶1 − 𝑉0 )𝑑𝑡 =>
𝑇 0
𝑇 0
+
𝑇𝑂𝐹𝐹
(2𝑉𝑖
𝑇
− 2𝑉𝐶1 − 2𝑉0 ) = 0 => {Sabemos que
𝑇𝑂𝑁
𝑇
= 𝐷 y que
𝑇𝑂𝐹𝐹
𝑇
=
(1 − 𝐷), reemplazando estos valores nos queda}:
𝑉𝐶1 =
𝐷𝑉𝑖 − (1 − 𝐷)2𝑉𝑜 + 2𝑉𝑖 (1 − 𝐷) 𝑉𝑖 (2 − 𝐷)
=
− 𝑉𝑜
2(1 − 𝐷)
2(1 − 𝐷)
Ahora nos fijamos en el caso de la bobina L2:
< 𝑉𝐿2 > =
< 𝑉𝐿2 > =
𝑇𝑂𝑁
𝑉𝐶1
𝑇
1 𝑇𝑂𝑁
1 𝑇2 +𝑇3
∫ 𝑉𝐶1 𝑑𝑡 + ∫
−𝑉0 + 𝑉𝐶1 𝑑𝑡 =>
𝑇 0
𝑇 0
+
𝑇𝑂𝐹𝐹
(𝑉𝐶1
𝑇
− 𝑉𝑜 ) => {
𝑇𝑂𝑁
𝑇
=𝐷y
𝑇𝑂𝐹𝐹
𝑇
= (1 − 𝐷)}:
𝑉𝑜 (1 − 𝐷) = 𝐷𝑉𝐶1 + 𝑉𝐶1 (1 − 𝐷) => Despejamos 𝑉𝐶1 para poder igualar esta ecuación a la
calculada anteriormente:
𝑉𝐶1 = 𝑉𝑜 (1 − 𝐷)
Las igualamos:
𝑉𝑖 (2 − 𝐷)
− 𝑉𝑜 = 𝑉𝑜 (1 − 𝐷)
2(1 − 𝐷)
Finalmente despejamos la expresión
𝑉𝑜
𝑉𝑖
para ver la relación de tensiones en este modo:
𝑉𝑜
1
=
𝑉𝑖
2(1 − 𝐷)
- Corrección del ciclo de trabajo por elementos reales para el Modo Continuo:
Para resolver esta parte, tenemos que tener en consideración tanto las resistencias internas de
los componentes que forman el circuito, para el que tiene el interruptor cerrado (Sw ON) y el
que lo tiene abierto (Sw OFF), así como la caída de voltaje en el diodo en el caso de que Sw
OFF y la caída de voltaje en Sw en el caso que Sw ON.
Resistencias en serie de las bobinas: 𝑅𝐿1 , 𝑅𝐿2
Reactancias de los condensadores: 𝐸𝑆𝑅1 , 𝐸𝑆𝑅2
Caídas de tensión producidas en el interruptor y el diodo, respectivamente: 𝑣𝑆𝑤 , 𝑣𝑑
Para el caso que Sw ON, tenemos el siguiente circuito:
De él deducimos las siguientes relaciones:
𝑣𝐿1 = 𝑉𝑖 − 𝑖𝐿1 𝑅𝐿1 − 𝑉𝑆𝑤
𝑣𝐿2 = 𝑉𝐶1 − 𝐸𝑆𝑅1 𝑖𝐶1 − 𝑖𝐿2 𝑅𝐿2
𝑖𝐶1 = 𝑖𝐿2
𝑖𝐶2 = 𝑖𝑜
Para el caso que Sw OFF, tenemos el siguiente circuito:
Deducimos las siguientes relaciones:
𝑣𝐿1 = 𝑉𝑖 − 𝑖𝐿1 𝑅𝐿1 − 𝑉𝐶1 − 𝐸𝑆𝑅1 𝑖𝐶1 + 𝑉𝑜
𝑉𝐿2 = 𝑣𝑑 − 𝑖𝐿2 𝑅𝐿2 − 𝑉𝑜
𝑖𝐿1 = 𝑖𝐶1
𝑖𝐿2 = 𝑖𝑖 − 𝑖𝐶2 − 𝑖𝑜
𝑉𝑅𝐿1 = 𝑖𝐿1 𝑅𝐿1
𝑉𝑅𝐿2 = 𝑖𝐿2 𝑅𝐿2
𝑉𝑅𝐶1 = 𝑖𝐿1 𝐸𝑆𝑅1
Calculamos de nuevo la relación entre el voltaje de entrada y de salida, para ello hacemos el
valor medio del voltaje en ambas bobinas, el cual tiene que ser 0 (mismo método que antes):
< 𝑉𝐿 > = 0
< 𝑉𝐿 > =
1 𝑇𝑂𝑁
1 𝑇
𝑉𝐿1𝑂𝑁 𝑑t + 𝑇 ∫0 𝑂𝐹𝐹 𝑉𝐿1𝑂𝐹𝐹 𝑑𝑡
∫
𝑇 0
=> Sustituimos a partir de las relaciones
deducidas en los circuitos... =>
< 𝑉𝐿1 > =
1 𝑇𝑂𝑁
1 𝑇𝑂𝐹𝐹
∫ (𝑉𝑖 − 𝑣𝑆𝑤 − 𝑉𝑅𝐿1 ) 𝑑𝑡 + ∫
𝑉𝑖 − 𝑣𝑑 − 𝑉𝐶1 − 𝑉𝑅𝐿1 − 𝑉𝑅𝐶1 − 𝑉𝑜 )𝑑𝑡 =>
𝑇 0
𝑇 0
< 𝑉𝐿1 > =
𝑇𝑂𝑁
𝑇𝑜𝑓𝑓
𝑉𝑖 − 𝑣𝑆𝑤 − 𝑉𝑅𝐿1 +
𝑉𝑖 − 𝑣𝑑 − 𝑉𝐶1 − 𝑉𝑅𝐿1 − 𝑉𝑅𝐶1 − 𝑉𝑜 =>
𝑇
𝑇
Todo esto será igual a 0, y sabemos que Ton/T = D y Toff/T = 1-D. Despejamos VC1:
𝑉𝐶1 =
𝑉𝑖 − 𝐷𝑣𝑆𝑤 − 𝑉𝑅𝐿1 − (1 − 𝐷)(𝑣d + 𝑉𝑅𝐶1 +𝑉𝑜 )
(1 − 𝐷)
Ahora hacemos lo mismo respecto a la bobina L2:
< 𝑉𝐿2 > =
1 𝑇𝑂𝑁
1 𝑇𝑂𝐹𝐹
∫ 𝑉𝐶1 − 𝑉𝑅𝐶1 − 𝑉𝑅𝐿1 𝑑𝑡 + ∫
𝑣𝑑 − 𝑉𝑜 − 𝑉𝑅𝐿2 𝑑𝑡 =
𝑇 0
𝑇 0
=
𝑇𝑂𝑁
𝑇𝑂𝐹𝐹
(𝑣𝑑 − 𝑉𝑜 − 𝑉𝑅𝐿2 ) =>
(𝑉𝐶1 − 𝑉𝑅𝐶1 − 𝑉𝑅𝐿1 ) +
𝑇
𝑇
=> 𝐷 (𝑉𝐶1 − 𝑉𝑅𝐶1 − 𝑉𝑅𝐿1 ) + (1 − 𝐷)(𝑣𝑑 − 𝑉𝑜 − 𝑉𝑅𝐿2 ) = 0 => Despejamos VC1:
𝑉𝐶1 =
(1 − 𝐷)(𝑣𝑑 − 𝑉𝑜 ) − 𝐷𝑉𝑅𝐶1 − 𝑉𝑅𝐿2
𝐷
Ahora igualamos ambas ecuaciones para obtener la relación de voltajes en este caso:
𝑉𝑖 − 𝐷𝑣𝑆𝑤 − 𝑉𝑅𝐿1 − (1 − 𝐷)(𝑣𝑑 + 𝑉𝑅𝐶1 +𝑉𝑜 ) (1 − 𝐷)(𝑣𝑑 − 𝑉𝑜 ) − 𝐷𝑉𝑅𝐶1 − 𝑉𝑅𝐿2
=
=>
(1 − 𝐷)
𝐷
=> 𝐷(𝑉𝑖 − 𝐷𝑣𝑆𝑤 − 𝑉𝑅𝐿1 − (1 − 𝐷)(𝑣𝑑 + 𝑉𝑅𝐶1 +𝑉𝑜 )) = (1 − 𝐷)((1 − 𝐷)(𝑣𝑑 − 𝑉𝑜 ) − 𝐷𝑉𝑅𝐶1 − 𝑉𝑅𝐿2 )=>
=> 𝑉𝑜 =
𝐷(𝑉𝑖 − 𝑉𝑅𝐿1 − 𝐷𝑣𝑆𝑤 − 𝑣𝑑 − 𝑉𝑅𝐿2 ) + (2𝐷 − 1)𝑣𝑑
=>
2𝐷 2 + 3𝐷 − 1
𝑉𝑜 D(𝑉𝑖 − 𝑉𝑅𝐿1 − 𝐷𝑣𝑆𝑤 − 𝑣𝑑 − 𝑉𝑅𝐿2 ) + (2𝐷 − 1)𝑣𝑑
=
𝑉𝑖
𝑉𝑖 (2𝐷2 + 3𝐷 − 1)
- Rendimiento del convertidor en modo continuo:
El rendimiento viene dado por la relación entre la potencia de salida y la de entrada, es decir:
𝜂=
Sabemos que 𝐼𝐿1 =
𝑉𝑜 𝐼𝑜
𝑉𝑖
=
𝐷
𝐼
1−𝐷 𝑜
𝑃𝑜
𝑉𝑜 𝐼𝑜
=
𝑃𝑖
𝑉𝑖 𝐼𝑖
= 𝐼𝑖 , sustituimos en la ecuación del rendimiento:
𝜂=
𝑉𝑜 𝐼𝑜
(1 − 𝐷)
= (𝑀
)
𝐷
𝐷
𝑉𝑖 1 − 𝐷 𝐼𝑜
Donde M es la relación de voltajes para cuando usamos componentes reales en el circuito.
Sustituimos dicha relación (ya calculada) y despejamos finalmente el rendimiento:
𝜂= (
𝐷(𝑉𝑖 − 𝐷𝑉𝑆𝑤 − 𝑉𝑅𝐿1 − 𝑣𝑑 − 𝑉𝑅𝐿2 ) + (2𝐷 − 1)𝑣𝑑 1 − 𝐷
)
𝑉𝑖 (2𝐷 2 + 3𝐷 − 1)
𝐷
Selección de componentes:
- Selección del diodo:
Debemos saber la corriente que tiene que soportar el diodo, por ello calculamos la corriente
de pico o máxima que va a pasar por él. Utilizaremos la condición crítica de paso de modo
continuo a discontinuo en el circuito:
𝐼𝐿1 −
∆𝑖𝐿1
2
− 𝐼𝐿2 −
∆𝑖𝐿2
2
𝐼𝑑𝑀𝐴𝑋 = 𝐼𝐿1 −
𝐼𝑑𝑀𝐴𝑋
≥ 0 => Condición crítica
∆𝑖𝐿1
∆𝑖𝐿2
− 𝐼𝐿2 −
=>
2
2
𝐷
𝑉𝑖 𝐷
𝑉𝑜 (1 − 𝐷)
𝐷
𝑉𝑖 𝐷
=
𝐼𝑜 −
− 𝐼𝑜 +
= 𝐼𝑜 (
− 1) −
+
1−𝐷
2𝐿1 𝑓
2𝐿2 𝑓
1−𝐷
2𝐿1 𝑓
𝐷𝑉𝑖 (1 − 𝐷)
(1 − 𝐷)
2𝐿2 𝑓
=>
2𝐷 − 1
𝑉𝑖 𝐷 1
1
=>𝐼𝑑𝑀𝐴𝑋 = 𝐼𝑜 (
)−
( − )
1−𝐷
2𝑓 𝐿1 𝐿2
Calculamos ahora su corriente media, fijándonos que el diodo sólo conduce durante Toff:
𝐼𝑑 =
1 𝑇𝑂𝐹𝐹
𝐼𝐿1 𝑑𝑡
∫
𝑇 0
−
1 𝑇𝑂𝐹𝐹
𝐼𝐿2 𝑑𝑡
∫
𝑇 0
= (1 − 𝐷)𝐼𝐿1 − (1 − 𝐷)𝐼𝐿2 => Sabemos los valores de
IL1 e IL2, los sustituimos para despejar:
𝐼𝑑 = (1 − 𝐷)
𝐷
𝐼 − (1 − 𝐷)𝐼𝑜 =>𝐼𝑑 = (2𝐷 − 1)𝐼𝑜
1−𝐷 𝑜
Ahora calculamos la tensión de bloqueo del diodo, que se producirá cuando el interruptor esté
cerrado, es decir, durante Ton. La tensión de bloqueo que soportará el diodo es Vc1, lo
deducimos así:
𝑉𝐵𝑑 = 𝑉𝑆𝑤 − 𝑉𝐶1 => 𝑉𝐵𝑑 > 𝐾(𝑉𝑖 + |𝑉𝑜 | − 𝑉𝑆𝑤 )
Donde K es el llamado factor de seguridad, que debe tomar un valor de 1,25 ≤ K ≤ 2.
- Selección del interruptor:
Sabemos que la máxima corriente que pasará por el interruptor es IL1, ya que solo conduce
cuando el circuito está en ON, por tanto:
𝐼𝑆𝑤𝑀𝐴𝑋 = 𝐼𝑑𝑀𝐴𝑋
Calculamos su valor medio:
𝐼𝑆𝑤 =
1 𝑇𝑂𝑁
∫ (𝐼𝐿1 − 𝐼𝐿2 )𝑑𝑡 =𝐼𝐿1 = 𝐼𝑖
𝑇 0
La tensión de bloqueo del interruptor se corresponde a cuando el circuito está en OFF, en la
rama del interruptor se produce la caída de la tensión de bloqueo 𝑉𝐵𝑆𝑤 = 𝑣𝑑 − 𝑉𝐶1.
Suponemos que 𝑉𝐶1 = 𝑉𝑖 + |𝑉0 |, ya que el condensador está descargado, de modo que le llega
la máxima tensión posible (𝑉𝑖 + |𝑉0 |). Nos queda que:
𝑉𝑅𝑆𝑤 = 𝑣𝑑 + 𝑉𝑖 + |𝑉𝑜 |
- Corriente eficaz por los condensadores
Calculamos la corriente eficaz por los condensadores a partir de la fórmula:
1 𝑇
𝐼𝑅𝑀𝑆 = √ ∫ 𝐼 2 𝑑𝑡
𝑇 0
Para el condensador C1:
1
𝑇
𝐼𝐶1𝑅𝑀𝑆 = √𝑇 ∫0 𝑂𝑁 −𝐼𝐿2 2 𝑑𝑡 +
𝐼𝐿1 =
𝐷𝐼𝑜
(1−𝐷)
1 𝑇𝑂𝐹𝐹
𝐼𝐿1 2 𝑑𝑡
∫
𝑇 0
= √𝐷𝐼𝐿2 2 + (1 − 𝐷)𝐼𝐿1 2 => {Sabemos que
y que 𝐼𝐿2 = 𝐼0 }
𝐼𝐶1𝑅𝑀𝑆
= √𝐷(𝐼𝑜 )2 + (1 − 𝐷) (
2
𝐷
𝐷2
𝐼0 ) = 𝐼0 √
+ 𝐷 =>
(1 − 𝐷)
(1 − 𝐷)
𝐷2
=> 𝐼𝐶1𝑅𝑀𝑆 = 𝐼0 √
+𝐷
(1 − 𝐷)
Para el condensador C2:
1
𝑇
𝐼𝐶2𝑅𝑀𝑆 = √𝑇 ∫0 𝑂𝑁 −𝐼𝑜 2 𝑑𝑡 +
=> √DIo 2 +
1 TOFF
(Ii
∫
T 0
1 𝑇𝑂𝐹𝐹
(𝐼i
∫
𝑇 0
− IL2 − Io )2 dt => {Sabemos que IL2 = -Io}
+ Io − Io )2 dt = √−DIo 2 + (1 − D)(Ii )2 => {Sabemos que IL1 =
DIo
}
(1−D)
2
D
D2
=> IC2RMS = √DIo 2 + (1 − D) (
Io ) = Io √D +
=>
(1 − D)
(1 − D)
=>IC2RMS = Io √D +
D2
(1 − D)
- Criterio para elegir el valor de C1:
Sabemos que la tensión no debe variar mucho en los condensadores, vamos a suponer que
∆vC1 < 0,1VC1 . Sabiendo esto y que ∆vC1 =
Io D
C1 f
V
i
y que VC1 = 1−D
− Vo , podemos sustituir en
la relación, quedándonos lo siguiente:
Io D
Vi
< 0,1 (
− Vo )
C1 f
1−D
Despejo C1 para saber la capacidad mínima que deberá tener el condensador:
1
Vi
f
1
Vi
Vi D
f
< 0,1 (
− Vo )
=>
< 0,1 (
−
)
=>
(1 − D) (1 − D) Io D
C1
1−D
Io D
C1
(1 − D)Vi − Vi D f
1
> 0,1 (
)
(1 − D)
C1
Io D
C1 > (
(1 − D)Io D
)
(0,1(1 − D)Vi − 0,1Vi D)f)
Ejemplo y verificación de resultados:
Efectuamos la simulación para comprobar los resultados obtenidos:
Con esto podemos comprobar que la relación de voltajes (Vo/Vi) es correcta, ya que es
positiva (al igual que en nuestros cálculos).
Si miramos la simulación en modo continuo (en el interruptor) podemos observar lo siguiente:
Vemos que la intensidad por el interruptor cae a 0 justo cuando llega a T.
De aquí podemos sacar el parámetro TON y T, y así comprobar la relación de voltajes:
7,35
TONsim = 7,35 𝜇𝑠; 𝑇𝑠𝑖𝑚 = 12,5 𝜇𝑠 => 𝐷𝑠𝑖𝑚 = 12,5 = 0,59
La frecuencia será 1/T => 𝑓 = 80000 𝐻𝑧 = 80 𝑘𝐻𝑧
Aplicando la relación de voltajes, si tuviésemos 10 voltios en la entrada, a la salida tendríamos:
𝑉𝑜 =
𝐷𝑉𝑖
=>
(1 − 𝐷)
V0 =
0,59 ∗ 10
= 14,39 𝑉
0,41
Ahora veremos qué componentes debemos seleccionar para que la simulación funcione
correctamente, a partir de la condición de paso de Modo Continuo a Modo Discontinuo
tenemos:
𝐼𝑜 𝐿||1,2 ≥
𝑉𝑖 𝐷(1 − 𝐷)
2𝑓
Despejamos Io para saber la corriente que habrá a la salida:
𝐼𝑜 ≥
𝑉𝑖 𝐷(1 − 𝐷)
2𝑓𝐿||1,2
10 ∗ 0,59(0,41)
=
2 ∗ 80000 ∗ (
= 0,020158 A = 20 mA
1
)
1
1
−3 +
−3
1 ∗ 10
3 ∗ 10
Efectuando la simulación, vemos que a la salida tenemos aproximadamente 8 mA.
Sabemos que la corriente máxima en el diodo es también la corriente máxima en el
interruptor:
2𝐷 − 1
𝑉𝑖 𝐷 1
1
𝐼𝑑𝑀𝐴𝑋 = 𝐼𝑆𝑤𝑀𝐴𝑋 = 𝐼𝑜 (
)−
( − )
1−𝐷
2𝑓 𝐿1 𝐿2
Despejando, obtenemos que:
2 ∗ 0,59 − 1
10 ∗ 0,59
1
1
𝐼𝑑𝑀𝐴𝑋 = 0,02 (
)−
(
)
−3 −
1 − 0,59
2 ∗ 80000 1 ∗ 10
3 ∗ 10−3
= 8,78 ∗ 10−3 − 3,69 ∗ 10−5 (666,67) = 0,0158 𝐴 = 15,8 𝑚𝐴
En la simulación podemos ver que IdMAX = ISwMAX:
Pero vemos que la máxima intensidad llega a los 190 mA, no se acerca a la que hemos
calculado. Posiblemente se deba a un fallo de cálculo a la hora de formular la máxima
corriente por el diodo...
Para los condensadores, sabemos que VC1=Vi, por tanto si aplicamos 10 V a la entrada, en el
condensador C1 deberán haber 10V. En la simulación vemos que se trata de 10,5.
Observamos las intensidades por los condensadores:
Calculamos su corriente eficaz:
𝐷
0.59
|𝐼𝐶1𝑅𝑀𝑆 | = 𝐼𝑜 √
= 20 ∗ 10−3 √
= 0,024 𝐴 = 24 𝑚𝐴
(1 − 𝐷)
0.41
|𝐼𝐶2𝑅𝑀𝑆 | =
𝑉𝑖 . 𝐷
𝐿2 𝑓2√3
=
10 ∗ 0.59
1 ∗ 10−3
∗ 80000 ∗ 2√3
= 0,021 𝐴 = 21 𝑚𝐴
En la simulación vemos que |𝐼𝐶1𝑅𝑀𝑆 | = 17,1 𝑚𝐴 y |𝐼𝐶2𝑅𝑀𝑆 | = 17,1 𝑚𝐴
Para las bobinas, hacemos lo mismo:
Calculamos su corriente máxima:
𝐼𝐿1 =
𝐷
𝐼
1−𝐷 𝑜
=
0,59
∗
1−0,59
0,02 = 0,029 𝐴 = 29 𝑚𝐴 => En la simulación, 𝐼𝐿1 = 30 𝑚𝐴
𝐼𝐿2 = −𝐼0 = −20 𝑚𝐴=> En la simulación 𝐼𝐿2 = −20 𝑚𝐴
Para el modo discontinuo calculamos la tensión de salida con Vi=10V:
𝑉𝑜 =
𝑉𝑖
10
=
= 8,2𝑉
2(1 − 𝐷) 2(1 − 0,59)
Si miramos la simulación, vemos que 𝑉𝑜 = 16,2 𝑉, lo cual dobla a nuestro voltaje de salida
calculado.