BASES:

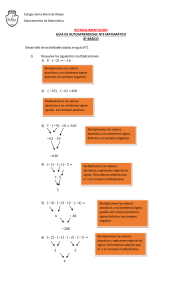
BASES:
En el sistema de bases no existen los números 10, 11, 12 (…), estos números son
sustituidos por letras de abecedario.
De tal modo que cuando nos encontremos “A” será 10,” B” será 11 y así sucesivamente.
Normalmente solo suele salir letras hasta la E (14).
Por lo cual los números son algo así:
1,2,3,4,5,6,7,8,9,A,B,C,D…
1. Pasar un número de base cualquiera(5,7,8…) a decimal:
Para pasar un número en una base cualquiera a decimal hacemos una descomposición
del número, empezando siempre por las unidades:
324(⁵ 
4.5⁰+2.5 ₁+3.5₂= 4+10+75=89
Notas:
(Cualquier número elevado a 0 es igual a 0, por lo que 4.5⁰=4)
(Multiplicamos por el número de 5 porque es la base del número)
BEBE (₁₆  E.16⁰+B.16₁+E.16₂+B.16₃= 14+176+3584+45056=48830
2. Pasar de base decimal a cualquier base:
Para pasar de decimal a otra base se divide el número entra la base hasta obtener un
cociente menor que este:
Por ejemplo para pasar el número 89 a base 5:
89 5
39 17 5
4
2
3
(El resultado es todos los restos de las divisiones de izquierda a derecha)
89= 324(⁵
3. Suma:
Para sumar dos números en bases solo podemos llegar al número anterior al de la
base:
6 5 3 (₇
5 5 6 (₇ +
--------------1 5 4 2 (₇
Para que nos sea más fácil primero nos fijamos en la base, en este caso 7, pues nos escribimos al lado de
la cuenta lo siguiente:
0
1
2
3
4 5 6
Siempre hasta el número anterior de la base.
Empezamos la suma: 3+ 6: 9, como el resultado se pasa de mi base que es nueve
volvemos a contar desde O.
0 1
2
.
.
.

3
4
5
6
Si contamos hasta nueve a partir del 6, que es el ultimo numero que me
permite esta base contar, vemos que me quedo en el número dos, por lo tanto
en el resultado tengo que poner 2 y me llevo una porque he dado una vuelta.
Continuamos, 5+5=10+1 que me llevo: 11. Pues cuento hasta once a partir de 6:
0
1
2
.
.
.


3
4
.
5
6
.
Me quedo en el cuatro, por lo que en el resultado de mi cuenta pongo 4 y me
llevo una.
En el caso que nos dé un número superior, imagina que el resultado nos da 18,
en este caso ya nos llevaríamos una, nos llevaríamos dos, porque hemos dado
dos vueltas y en mi cuenta tendría que poner el numero 4.
0 1 2 3 4 5 6
.
.
.
.
.
.
.
.
.
.
. .
4. Resta:
Para restar si no podemos quitar al de arriba, por ejemplo 1- 4, a uno no le podemos
quitar 4, por lo tanto tenemos que “pedir” al número de la izquierda uno, de tal modo
que ha ese número le resto 1 y al siguiente le sume el valor de la base en la que
estemos:
1
6
3 7
2 1 4 2(⁵
1 3 3 4(⁵ --------------0 3 0 3(⁵
Empezamos con la resta: 2- 4, como ha al número 2 no le puedo quitar 4 le quito al
número de la izquierda 1, de tal modo que el 4 se queda en 3, y al número 2 le sumo el
valor de la base: 5+2 =7, por lo que ya puedo hacer mi resta normal: 7-4= 3.
5. Multiplicación:
Para multiplicar hacemos lo mismo que con la suma, multiplicamos normal pero
cuando el resultado sea la base o un número mayor de la base tenemos que volver a
dar la vuelta:
2 3 1(₄
x 3
2(₄
----------------1 1 2 2
2 0 1 3
---------------------2 1 3 1 2 (₄
Empezamos con la multiplicación: 2x1 = 2, como no se pasa de la base 4 multiplicamos
normal y ponemos dos.
Luego viene 2x 3= 6, esta vez sí se pasa de mi base con que hacemos lo mismo que con
la suma:
0 1
2 3
.
.
.
En este caso en la multiplicación ponemos 2 y nos llevamos 1 por dar una vuelta.
El resto es lo mismo, y luego los resultados de la multiplicación se suman también en
base 4.
6. División:
La división es la mezcla de todo lo anterior.
3
1 2 3
2
3
0
2 2 3
2 0 1
2 1 (₄
2 3 (₄
10333(₄
0 2 2 2
2 0 1
0 2 1 1
1 1 1
0
1 0
Lo primero que hay que hacer en una división es hacer las multiplicaciones necesarias
que vamos a utilizar:
23 x 0 = 0
23 x 1= 23
23 x 2= 112
23 x 3 = 201
Empezamos con la división: 31 coge a 1, pues le restamos 23 que es el resultado de 23 x
1, nos da 022, este número como se pasa pues ponemos cero y bajamos cifra siguiente:
0223 este número si coge con el tres pues el resultado de la multiplicación de 23 x 3 se lo
restamos y así siempre….
(Las multiplicaciones que utilizamos y las restas son de bases, es decir no son normales).
7. Ecuaciones en base:
611(x = 456(x+1
1.X⁰+ 1.X₁+ 6.X₂= 6.(X+1) ⁰+ 5.(X+1) ₁+4. (X+1) ₂
1+X+6X₂=6+5X+5+4 (X₂+1+2X)
1+X+6X₂=6+5X+5+4X₂+4+8X
1+X+6X₂-6-5X-4X₂-4-8X=0
−𝑏 ± √𝑏 2 − 4𝑎𝑐 12 ± √122 − 4.2. (−14) 12 ± √144 + 12 12 ± 16
𝑥=
=
=
=
2𝑎
2.2
4
4
X1= 7
X2 = - 1
Es decir lo único que hay que hacer es descomponer cada número hasta que tengamos
los datos para resolver una ecuación de segundo grado, de la misma forma que
pasábamos de un numero en base a un numero decimal.
Empezando por la izquierda, en este caso: 1 por X elevado a 0, mas 1 por X elevado a
1….
Hay una forma de demostrar si es correcto el valor de X. Consiste en sustituir la X por
el valor de X en este caso 7 .