Ecuaciones diferenciales ordinarias: problemas de contorno

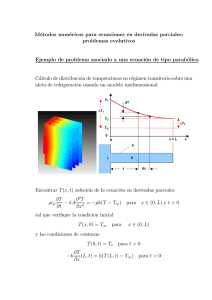
Ecuaciones diferenciales ordinarias: problemas de contorno
Formulación abstracta de problema lineal de segundo orden
Encontrar y(t) solución de la ecuación diferencial ordinaria (EDO)
α2 (x)
d2 y
dy
+
α
(x)
+ α0 (x)y = f (x) para x ∈ (a, b)
1
dx2
dx
tal que:
βa
dy
(a) + γa y(a) = δa
dx
y
βb
dy
(a) + γb y(a) = δb
dx
Algunas observaciones
• Bajo ciertas condiciones (sobre la regularidad y positividad de los
coeficientes) puede asegurarse la existencia y unicidad de solución
• En general (a pesar de que pueda garantizarse la existencia y unicidad de solución) este problema no puede resolverse analı́ticamente.
• El problema no lineal (de claro interés práctico) es (mucho) más
difı́cil de analizar
Alternativas para la resolución numérica
• Métodos de tiro
- usan técnicas para resolución de problemas de valor inicial
- se ajusta el valor de la condición inicial desconocida hasta que se
verifica la condición final
- su formulación se simplifica en el caso de problemas lineales
• Métodos de diferencias finitas
- usan técnicas de derivación numérica para aproximar la ecuación
diferencial (y las condiciones de contorno donde aparecen derivadas)
- se pueden extender a problemas de contorno asociados a ecuaciones en derivadas parciales
Ejemplo: cálculo de una aleta de refrigeración
Modelo unidimensional para cálculo de aleta
La temperatura estacionaria T (x) es solución de
−
d
dT
(kA ) = −ph(T − Tamb )
dx
dx
con unas (posibles) condiciones de contorno
T (0) = T0
y
−k
2
dT
(L) = h(T (L) − Tamb )
dx
Formulación de un esquema de diferencias finitas
• Se introducen varios puntos en el intervalo (0, L) donde se buscará una
aproximación de la temperatura
• Sobre cada uno los puntos interiores (2, 3, . . . n − 1) se busca una aproximación de la ecuación diferenencial
d2 T
−kA 2 = −ph(T − Tamb)
dx
Ası́, para cada nodo interior xi
se aproxima
−kA
Ti−1 − 2Ti + Ti+1
= −ph(xi)(Ti − Tamb )
(∆x)2
• Sobre el extremo izquierdo se impone la temperatura
T1 = T0
• Sobre el extremo derecho se impone el flujo de calor
−k
Tn − Tn−1
= h(xn)(Tn − Tamb)
∆x
3
Función aleta mdf programada en GNU Octave
• Llamada a función aleta mdf:
octave:> [x,T]=aleta mdf(L,A,p,k,T0,Tamb,fcnh,np);
donde (ayuda con help aleta mdf):
L: longitud de la aleta
A: sección (transversal) de la aleta
p: perı́metro (transversal) de la aleta
k: coeficiente de conducción térmica
T0: temperatura en extremo caliente
Tamb: temperatura ambiente
fcnh: función que describe el coeficiente de pelı́cula
np: número de puntos usados en discretización
• Ejemplo: aleta con coeficiente de convección constante
definición de función h(x) (archivo coefh.m)
function h = coefh(x)
h=10;
resolución y comparación con solución exacta:
octave:> L=1;k=1;A=1;p=1;T0=500;Tamb=300;
octave:> [x,T]=aleta mdf(L,A,p,k,T0,Tamb,"coefh",20);
octave:> xex=linspace(0,L,1000);
octave:> Tex=exacta(L,A,p,k,T0,Tamb,10,xex);
octave:> plot(x,T,"*",xex,Tex)
4
Ejemplo: cálculo de intercambio de calor en un tubo
Modelo unidimensional para cálculo de un tubo
Hipótesis de cálculo
• el fluido fuera de tubos no cambia de temperatura
• el coeficiente de transferencia es conocido (puede ser variable)
Modelo unidimensional estacionario
La temperatura estacionaria T (x) es solución de
d
dT
dT
− (kA ) = −ph(T − Tsteam)
ρcp U A
dx dx
dx
con unas (posibles) condiciones de contorno
dT
T (0) = T0
y
− k (L) = 0
dx
5
Formulación de un esquema de diferencias finitas
• Esquema centrado para derivada de primer orden
Aproximación del término convectivo en nodos interiores
ρcp U A
dT
dx
Alternativa con aproximación de segundo orden:
ρcp U A
Ti+1 − Ti−1
2∆x
• Esquema completo para la aproximación de la solución
• En el extremo izquierdo (temperatura impuesta)
T1 = T0
• En los nodos intermedios (aproximación del balance)
ρcp U A
Ti+1 − Ti−1
Ti−1 − 2Ti + Ti+1
= −ph(xi)(Ti − Tsteam)
− kA
2∆x
(∆x)2
• En el extremo derecho (flujo de calor por conducción nulo)
−k
Tn − Tn−1
=0
∆x
• Función tubo mdf programada en GNU Octave
octave:> L=1;k=1;A=1;p=1;T0=300;Tamb=500;rho=1;cp=1;U=10;
octave:> [x,T]=tubo mdf(L,A,p,rho,cp,k,T0,U,Tamb,"coefh",20);
octave:> plot(x,T,"*")
6
Resolución de problema con convección fuerte
• Cálculo de temperaturas con velocidad elevada
Cálculo de tubo en intercambiador con velocidad U = 100
octave:> L=1;k=1;A=1;p=1;T0=300;Text=500;rho=1;cp=1;U=100;
octave:> [x,T]=tubo mdf(L,A,p,rho,cp,k,T0,U,Text,"coefh",20);
octave:> plot(x,T,"*")
• Otro ejemplo numérico con número de Péclet alto
Cálculo térmico en tubo con descarga a depósito
La temperatura estacionaria T (x) es solución de
ρcp U A
d
dT
dT
− (kA ) = −ph(T − Tsteam)
dx dx
dx
con condiciones de contorno
T (0) = Tin
y
T (L) = Tout
Cálculo de temperaturas con función de GNU Octave descarga mdf
octave:> L=1;k=1;A=1;p=1;Tin=300;Text=500;...
> Tout=400;rho=1;cp=1;U=100;
octave:> [x,T]=descarga mdf(L,A,p,rho,cp,k,Tin,...
> Tout,U,Text,"coefh",20);
octave:> plot(x,T,"*")
7
• Resolución de problemas con fuerte convección
• Una alternativa poco eficiente
Cálculo con función descarga mdf y paso reducido
octave:> [x,T]=descarga mdf(L,A,p,rho,cp,k,Tin,...
> Tout,U,Text,"coefh",200);
octave:> plot(x,T,"*")
• Esquema descentrado para términos convectivos
Aproximación del término convectivo en nodos interiores
dT
ρcp U A
dx
basado en esquema con más sentido fı́sico (U > 0)
Ti − Ti−1
ρcp U A
∆x
donde se sacrifica precisión (primer orden)
• Resultados numéricos esquema descentrado
Cálculo de temperaturas con función de GNU Octave descarga mdf2
octave:> L=1;k=1;A=1;p=1;Tin=300;Text=500;...
> Tout=400;rho=1;cp=1;U=100;
octave:> [x,T]=descarga mdf2(L,A,p,rho,cp,k,Tin,...
> Tout,U,Text,"coefh",20);
octave:> plot(x,T,"*")
8