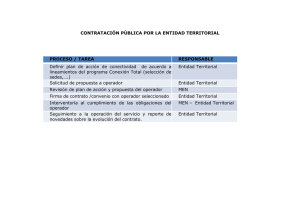
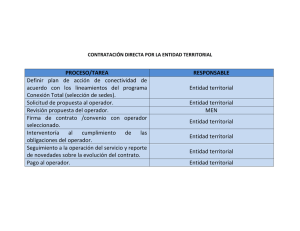
a de operadores no acotados surge como

VII. OPERADORES NO
ACOTADOS EN ESPACIOS
DE HILBERT
La teorı́a de operadores no acotados surge como necesidad de
establecer los fundamentos matemáticos de la Mecánica Cuántica
y fue desarrollada en los años 1920-1930 por von Neumann y Stone. Sus principales aplicaciones, aparte de la Mecánica Cuántica, se dirigen al estudio de las ecuaciones diferenciales. Sirva
este capı́tulo para mostrar las propiedades fundamentales de los
operadores no acotados, destacando las diferencias y nuevas dificultades que aparecen al eliminar la condición de acotación en los
operadores, en especial el problema de extensión que aquı́ aparece.
SECCIONES
1. Introducción. Operadores simétricos y autoadjuntos.
2. Propiedades espectrales de operadores simétricos y autoadjuntos.
3. Teorema espectral de operadores unitarios.
4. Teorema espectral de operadores autoadjuntos no acotados.
5. Ejercicios.
289
1. INTRODUCCIÓN. OPERADORES SIMÉTRICOS Y AUTOADJUNTOS.
Los dos ejemplos básicos de operadores no acotados son el operador multiplid
cación M f (x) = x · f (x) y el operador derivación Df (x) = dx
f (x), definidos
2
en L (R), operadores para los que se cumple la relación de conmutación
DM − M D = I, fórmula en la que se basa el principio de incertidumbre de
la Mecánica Cuántica. Se puede probar además que la relación anterior no
se da en ninguna pareja de operadores acotados (ver los ejercicios al final
del capı́tulo) y los operadores que la cumplen se pueden identificar con los
anteriores.
El primer resultado que enunciamos es uno de los primeros teoremas del
Análisis Funcional (1910) y sugiere que el dominio de un operador y el problema de extensión del mismo juegan un importante papel en la cuestión de
su acotación.
1.1.- Teorema (Hellinger-Toeplitz). Sea H un espacio de Hilbert y supongamos que T : H → H es un operador lineal definido en todo H y simétrico,
es decir tal que hT x, yi = hx, T yi, ∀x, y ∈ H. Entonces T es acotado.
En particular, como el operador multiplicación verifica
Z
hM f, gi =
xf (x) g(x)dx = hf, M gi
R
y no es acotado, no puede estar definido en todo el espacio.
Demostración. Supongamos por el contrario que existe una sucesión de Cauchy (yn )n∈N en H con kyn k = 1 y kT yn k → ∞. Definimos la sucesión (fn )n∈N
de funcionales lineales en H por fn (x) = hT x, yn i = hx, T yn i, ∀n.
Por la desigualdad de Schwarz, |fn (x)| = |hx, T yn i| ≤ kT yn k · kxk, de modo
que cada fn está acotado.
Además, de |fn (x)| = |hT x, yn i| ≤ kT xk de deduce que (fn (x))n∈N es una sucesión acotada. Por el principio de acotación uniforme (capı́tulo IV, teorema
4.2), (kfn k)n∈N está acotada, por lo que kfn k ≤ k, ∀n. Ası́
|fn (x)| ≤ kfn k · kxk ≤ kkxk.
En particular, para x = T yn resulta que
kT yn k2 = hT yn , T yn i = |fn (T yn )| ≤ kkT yn k =⇒ kT yn k ≤ k
lo que es absurdo.
♦
Observaciones. 1) El teorema anterior sugiere plantear el problema de
determinar dominios de operadores y obtener extensiones de los mismos.
290
Utilizaremos la notación S ⊂ T para indicar que T es extensión de S, es decir
D(S) ⊂ D(T ) y T |D(S) = S. Es claro que S ⊂ T si y sólo si G(S) ⊂ G(T ),
donde G representa el grafo del operador.
2) Si un operador lineal es acotado, es decir
∃k > 0 : kT xk ≤ kkxk, ∀x ∈ D(T ),
puede extenderse a D(T ) por continuidad. Si D(T ) no fuera denso en H,
se puede extender T más allá de D(T ), haciendo por ejemplo T x = 0,
∀x ∈ D(T )⊥ , y por linealidad definirlo en todo H. Dicha extensión estará también acotada y tendrá la misma norma de T . Esto sugiere suponer
que los operadores lineales acotados están siempre definidos en todo H, de
modo que en lo sucesivo adoptaremos dicho convenio.
A continuación vamos a generalizar el concepto de operador adjunto en el
caso de operadores no acotados.
1.2.- Definición. Dado un operador lineal T con dominio D(T ) ⊂ H, se
define
D(T ∗ ) = {x0 ∈ H : ∃y 0 , hT x, x0 i = hx, y 0 i, ∀x ∈ D(T )}
y se llama adjunto de T al operador T ∗ definido por
∀x0 ∈ D(T ∗ ) : T ∗ x0 = y 0 .
1.3.- Proposición. T ∗ está bien definida (es decir y 0 es único) si y sólo si
D(T ) es denso en H.
Demostración. Si D(T ) 6= H, existe y1 ∈ H con y1 6= 0 tal que y1 ⊥D(T ).
Ası́ hx, y 0 i = hx, y 0 i + hx, y1 i.
Recı́procamente, si D(T ) = H e y1 = T ∗ x, y2 = T ∗ x, entonces
hy1 , zi = hy2 , zi, ∀z ∈ D(T ) =⇒ y1 − y2 ⊥D(T ) =⇒ y1 − y2 ⊥H =⇒ y1 = y2 .
Observaciones. De la definición se deducen también las propiedades correspondientes al caso en que los operadores son acotados. En particular:
1) ∀x ∈ D(T ), x0 ∈ D(T ∗ ) : hT x, x0 i = hx, T ∗ x0 i.
2) Si T ∈ L(H), entonces T ∗ ∈ L(H) y kT ∗ k = kT k.
3) Si T ∈ L(H), entonces T ∗∗ = T .
4) Si S, T ∈ L(H), T ∗ S ∗ = (ST )∗ .
5) Si α ∈ C y T tiene dominio denso en H, entonces (αT )∗ = αT ∗ .
Sin embargo, para operadores no acotados se presentan ciertas diferencias
como se muestra a continuación.
291
1.4.- Proposición. Sean S y T dos operadores lineales con dominio denso
en el mismo espacio de Hilbert H.
a) Si S ⊂ T , entonces T ∗ ⊂ S ∗ .
b) T ∗ + S ∗ ⊂ (T + S)∗ .
c) Si ST tiene dominio denso en H, entonces T ∗ S ∗ ⊂ (ST )∗ . Si además
S ∈ L(H), entonces T ∗ S ∗ = (ST )∗ .
Demostración. a) Si x ∈ D(T ∗ ), entonces existe y ∈ H tal que hx, T zi =
hy, zi, ∀z ∈ D(T ). Como S ⊂ T , hy, zi = hx, T zi = hx, Szi, ∀z ∈ D(S). Esto
implica que x ∈ D(S ∗ ) y S ∗ x = y, o bien que T ∗ ⊂ S ∗ .
b) Si x ∈ D(T ∗ + S ∗ ), entonces x ∈ D(T ∗ ) y x ∈ D(S ∗ ). Por tanto,
∃y1 , y2 ∈ H : h x, T zi = hy1 , zi, ∀z ∈ D(T )
h x, Szi = hy2 , zi, ∀z ∈ D(S)
=⇒ h x, (T + S)zi = hy1 + y2 , zi, ∀z ∈ D(T ) ∩ D(S) = D(T + S).
Esto implica que x ∈ D(T + S)∗ y (T + S)∗ x = y1 + y2 = (T ∗ + S ∗ )x.
c) Si x ∈ D(T ∗ S ∗ ) =⇒ x ∈ D(S ∗ ), S ∗ x ∈ D(T ∗ ). Por tanto,
∃y1 ∈ H : hx, Szi = hy1 , zi, ∀z ∈ D(S),
∃y2 ∈ H : hS ∗ x, T ui = hy2 , ui, ∀u ∈ D(T ),
Ahora bien, si u ∈ D(ST ), entonces u ∈ D(T ) y z = T u ∈ D(S). Teniendo
en cuenta que y1 = S ∗ x, tenemos:
hx, ST ui = hx, Szi = hy1 , zi = hS ∗ x, T ui = hy2 , ui
lo que implica que x ∈ D((ST )∗ ) y (ST )∗ x = y2 = T ∗ S ∗ x.
Por último, si S ∈ L(H), veamos que D((ST )∗ ) ⊂ D(T ∗ S ∗ ).
Sea pues x ∈ D((ST )∗ ). Entonces ∃y ∈ H : hx, (ST )zi = hy, zi, ∀z ∈ D(ST ).
En particular hx, (ST )zi = hy, zi, ∀z ∈ D(T ). Como S ∈ L(H), S ∗ ∈ L(H)
y hx, (ST )zi = hS ∗ x, T zi, lo que implica que S ∗ x ∈ D(T ∗ ). Como además
D(S ∗ ) = H, también x ∈ D(S ∗ ); por tanto x ∈ D(T ∗ S ∗ ).
♦
Una generalización del concepto de operadores simétricos para operadores
no acotados es la siguiente:
1.5.- Definición. Un operador T : D(T ) ⊂ H → H es simétrico si
hT x, yi = hx, T yi, ∀x, y ∈ D(T ).
Un operador simétrico es maximal si no tiene extensiones simétricas propias.
292
Observación. A veces se exige que un operador simétrico tenga dominio
denso y, en caso de no cumplir esta condición, recibe el nombre de operador
hermı́tico.
Las siguientes caracterizaciones de los operadores simétricos son útiles.
1.6.- Proposición. Si D(T ) = H, son equivalentes:
i) T es simétrico.
ii) T ⊂ T ∗ .
iii) hT x, xi ∈ R, ∀x ∈ D(T ).
Demostración. i) =⇒ ii). Sea x ∈ D(T ). Existe entonces y = T x tal que
hT z, xi = hz, yi, para todo z ∈ D(T ). Esto implica que x ∈ D(T ∗ ) y que
T ∗ x = y = T x.
ii) =⇒ iii). Si x ∈ D(T ), hT x, xi = hT ∗ x, xi = hx, T xi = hT x, xi. Esto
implica que hT x, xi ∈ R.
iii) =⇒ i). Sea α ∈ C. Entonces
hT (x + αy), x + αyi = hT x, xi + αhT y, xi + αhT x, yi + α αhT y, yi
hx + αy, T (x + αy)i = hx, T xi + αhy, T xi + αhx, T yi + α αhy, T yi.
Teniendo en cuenta que hT (x + αy), x + αyi = hx + αy, T (x + αy)i, resulta:
Para α = 1, hx, T yi+hT x, yi = hT x, yi+hx, T yi =⇒ ImhT x, yi = Imhx, T yi.
Para α = i, hx, T yi+hx, T yi = hT x, yi+hT x, yi =⇒ Rehx, T yi = RehT x, yi.
De las dos igualdades se deduce que hT x, yi = hx, T yi.
♦
1.7.- Definición. Un operador T : D(T ) ⊂ H → H con dominio denso en
H es autoadjunto si T = T ∗ .
Es evidente entonces que todo operador autoadjunto es simétrico y si D(T ) =
H, el recı́proco también es cierto.
De la definición se deduce también que todo operador simétrico T que verifica
D(T ) = D(T ∗ ) es autoadjunto.
d
el operador definido en el
Ejemplos. 1) Sea H = L2 (R) y D = i · dx
conjunto de funciones que tienen lı́mite cero en los infinitos (que es denso
en H). Entonces D es simétrico.
2) Sea H = L2 [0, 1] y se define Tk f = i · f 0 , (k = 1, 2, 3), con
D(T1 ) = {f ∈ H : f absolutamente continua y f 0 ∈ H},
D(T2 ) = {f ∈ D(T1 ) : f (0) = f (1)} ⊂ D(T1 ),
D(T3 ) = {f ∈ D(T2 ) : f (0) = f (1) = 0} ⊂ D(T2 ),
293
dominios que definen varios aspectos del problema de la cuerda vibrante.
Se observa en primer lugar que T3 ⊂ T2 ⊂ T1 . Tenemos además que T1∗ =
T3 , T2∗ = T2 , T3∗ = T1 . Resulta pues que T2 es extensión autoadjunta del
operador simétrico T3 y T1 es una extensión no simétrica de T2 . Esto indica
en particular que los conceptos de operador simétrico y autoadjunto no
coinciden en el caso de operadores no acotados. Observemos además que el
cálculo del operador adjunto depende del dominio del operador y no basta
la definición formal del mismo.
En un espacio de Hilbert arbitrario H, la aplicación U : H × H → H × H,
definida por U (x, y) = i(y, −x), llamado operador de conjugación, es un
operador unitario tal que U 2 = I; además tenemos lo siguiente:
1.8.- Proposición. Sea T : D(T ) ⊂ H → H un operador lineal con D(T ) =
H.
a) Si G(T ) = {(x, T x) : x ∈ D(T )} es el grafo de T , entonces U (G(T ))⊥ =
G(T ∗ ).
b) Si T admite una clausura, entonces su adjunto T ∗ tiene dominio denso
en H y U (G(T ∗ ))⊥ = G(T ∗∗ ).
Demostración. a) Supongamos que (x, y) ∈ U (G(T ))⊥ . Entonces,
∀(u, v) ∈ U (G(T )), h(x, y), (u, v)i = 0.
Como (u, v) = U (a, T a) = (iT a, −ia) para algún a ∈ D(T ), resulta:
0 = h(x, y), (u, v)i = hx, ui + hy, vi = hx, iT ai + hy, −iai
= −ihx, T ai + ihy, ai =⇒ hx, T ai = hy, ai.
Esto implica que x ∈ D(T ∗ ) y que y = T ∗ x.
Recı́procamente, si (x, y) ∈ G(T ∗ ), x ∈ D(T ∗ ), y = T ∗ x. Por tanto, para
todo a ∈ D(T ),
h(x, y), (iT a, −ia)i = −ihx, T ai + ihy, ai = −ihT ∗ x, ai + ihy, ai = 0.
b) Supongamos que D(T ∗ ) 6= H, es decir ∃y0 6= 0 : y0 ⊥D(T ∗ ). Entonces
hy0 , xi = 0, ∀x ∈ D(T ∗ ), de donde
h(y0 , 0), (x, T ∗ x)i = 0, ∀x ∈ D(T ∗ ) =⇒ (y0 , 0) ∈ G(T ∗ )⊥ .
Debido al apartado (a),
G(T ∗ )⊥ = U (G(T ))⊥⊥ = U (G(T )).
294
Por tanto, ∃(xn )n∈N ⊂ D(T ) tal que (y0 , 0) = lı́mn U (xn , T xn ), de donde
y0 = lı́m iT xn , 0 = lı́m −ixn .
n
n
Por ser T clausurable, si lı́mn ixn = 0, lı́mn iT xn = y0 , entonces y0 = 0, lo
que contradice la suposición inicial.
La segunda parte se obtiene de (a) sustituyendo T por T ∗ .
♦
La importancia de este teorema queda patente en la variedad de consecuencias que de él se derivan.
1.9.- Corolario. Sea T : D(T ) ⊂ H → H un operador lineal con dominio
denso en H.
1) T ∗ es cerrado. En particular los operadores autoadjuntos son cerrados.
2) Si D(T ∗ ) es también denso en H, T ⊂ T ∗∗ .
3) Si T es clausurable, entonces ( T )∗ = T ∗ , T = T ∗∗ . En particular, si T
es cerrado, T = T ∗∗ .
4) N (T ∗ ) = R(T )⊥ y, si T es cerrado, N (T ) = R(T ∗ )⊥ .
5) Si T es simétrico, es clausurable y T es también simétrico.
6) H × H = G(T ∗ ) ⊕ U G(T ).
−T x + y = a
siempre tiene solución (x, y) ∈
7) Si T es cerrado, el sistema
x + T ∗y = b
D(T ) × D(T ∗ ).
8) Si T es inyectiva y R(T ) es denso en H, entonces T ∗ es inyectiva y
∗
(T ∗ )−1 = (T −1 ) .
Demostración. 1) G(T ∗ ) es cerrado por ser el complemento ortogonal de un
subespacio de H × H.
2) Como U (G(T ))⊥ = G(T ∗ ), resulta
U (G(T )) = G(T ∗ )⊥ =⇒ U (G(T )) ⊂ G(T ∗ )⊥
=⇒ G(T ) ⊂ U (G(T ∗ )⊥ ) = G(T ∗∗ ) =⇒ T ⊂ T ∗∗ .
3) Si T es la clausura de T , G( T ) = G(T ). Entonces
∗
U (G( T )) = U (G(T )) =⇒ G(T ∗ ) = U (G(T ))⊥ = U (G( T ))⊥ = G( T ).
Por otra parte, de G(T ∗ ) = U (G(T ))⊥ deducimos que
G(T ∗ )⊥ = U (G(T ))⊥⊥ = U ( G(T )) = U (G( T ))
295
y de aquı́,
G(T ∗∗ ) = U (G(T ∗ ))⊥ = U (G(T ∗ )⊥ ) = U 2 (G( T )) = G( T ).
Esto prueba que T ∗∗ = T .
4) De lo anterior se deduce
x ∈ N (T ∗ ) ⇐⇒ (x, 0) ∈ G(T ∗ ) ⇐⇒ h(x, 0), (u, v)i = 0, ∀(u, v) ∈ U (G(T ))
⇐⇒ h(x, 0), (iT a, −ia)i = 0, ∀a ∈ D(T )
⇐⇒ hx, T ai = 0, ∀a ∈ D(T ) ⇐⇒ x ∈ R(T )⊥ .
5) Si T es simétrico, T ∗ es extensión de T y T ∗ es cerrado. Además, ∀x, y ∈
D( T ), ∃(xn )n∈N , (ym )m∈N ⊂ D(T ) tales que
xn → x, T xn → T x, ym → y, T ym → T y.
Ası́ pues,
h T x, yi = lı́mhT xn , ym i = lı́mhxn , T ym i = hx, T yi.
n,m
n,m
6) Es evidente pues G(T ∗ )⊥ = U (G(T )).
7) Sea (a, b) ∈ H × H arbitrario. Tenemos:
(a, b) = f + g, f ∈ G(T ∗ ), g ∈ U (G(T )) = U (G(T ))
(a, b) = (y, T ∗ y) + U (x0 , T x0 ), y ∈ D(T ∗ ), x0 ∈ D(T )
=⇒ (a, b) = (y, T ∗ y) + i(T x0 , −x0 ) = (y, T ∗ y) + (−T x, x), y ∈ D(T ∗ ), x ∈ D(T ).
⊥
8) Por el apartado (4), N (T ∗ ) = R(T )⊥ = R(T ) = {0}. Teniendo en
cuenta ahora la proposición 1.4, como D(T ) y D(T −1 ) = R(T ) son densos
en H, entonces
(T −1 )∗ T ∗ ⊂ (T T −1 )∗ = I =⇒ (T −1 )∗ = (T ∗ )−1 .
♦
Observación. Debido al apartado 5) se puede suponer siempre que un operador simétrico es cerrado.
La siguiente propiedad será también útil en el estudio de los operadores
autoadjuntos.
1.10.- Proposición. Sea T un operador simétrico con dominio denso en
H. Entonces:
a) D(T ) = H =⇒ T = T ∗ y T ∈ L(H).
296
b) T = T ∗ y T inyectivo =⇒ R(T ) = H y T −1 = (T −1 )∗ .
c) R(T ) = H =⇒ T inyectivo.
d) R(T ) = H =⇒ T = T ∗ y T −1 ∈ L(H).
Demostración. a) Por ser T simétrico, T ⊂ T ∗ . Como D(T ) = H, T = T ∗ .
Por el teorema del gráfico cerrado, como T es cerrado y D(T ) = H, T
es acotado. (Como se observa, esto constituye otra prueba del teorema de
Hellinger-Toeplitz.)
b) Debido al apartado 4 del corolario anterior, N (T ) = R(T )⊥ , de modo
que, si N (T ) = 0, entonces R(T ) = H.
La segunda parte se obtiene ahora aplicando el apartado 8 del corolario
citado.
c) Sea v ∈ D(T ) tal que T v = 0. Entonces:
hT v, xi = 0, ∀x ∈ D(T ) =⇒ hv, T xi = 0, ∀x ∈ D(T ) =⇒ v ∈ R(T )⊥ =⇒ v = 0.
d) Si R(T ) = H, T es inyectiva y existe S = T −1 con D(S) = R(T ) =
H.
Dados f, h ∈ R(T ), f = T g, h = T k, entonces
hSf, hi = hg, T ki = hT g, ki = hf, ki = hf, Shi,
es decir S es simétrico. Por el apartado a), S = S ∗ ∈ L(H) y, por el apartado
b), T = S −1 es autoadjunto.
♦
Estudiaremos a continuación el problema de las extensiones de operadores
simétricos. Sabemos que, si T es un operador simétrico y S es una extensión
simétrica de T , entonces T ⊂ S ⊂ S ∗ ⊂ T ∗ , es decir toda extensión simétrica
de T es restricción de T ∗ .
1.11.- Proposición. a) Todo operador simétrico tiene alguna extensión simétrica maximal.
b) Toda extensión simétrica maximal de un operador simétrico es cerrada.
c) Todo operador autoadjunto es simétrico maximal.
El apartado a) es una simple aplicación del lema de Zorn y los otros dos son
consecuencia de los resultados anteriores.
1.12.- Teorema. Sean T un operador simétrico y λ = a + ib con a, b ∈ R.
Entonces:
a) k(T − λI)xk2 = b2 kxk2 + k(T − aI)xk2 , ∀x ∈ D(T ).
297
b) Si b 6= 0, N (T − λI) = {0}, es decir T − λI es inyectivo.
c) Si b 6= 0 y T es cerrado, entonces R(T − λI) es cerrado.
d) Si además R(T − λI) = H, T es simétrico maximal.
Demostración. Observamos en primer lugar que
k(T −λI)xk2 = k(T −aI)x−ibxk2 = k(T −aI)xk2 +b2 kxk2 +2 Re ih(T −aI)x, bxi
donde h(T − aI)x, bxi = bhT x, xi − abkxk2 ∈ R. Esto demuestra el apartado
a).
De aquı́ también se deduce que (T − λI)x = 0 =⇒ b2 kxk2 = 0 =⇒ x = 0, lo
que prueba el apartado b).
Para probar c) elegimos una sucesión (xn )n∈N ⊂ D(T ) tal que (T − λI)xn →
y. Entonces (xn )n∈N es de Cauchy porque
b2 kxn −xm k2 ≤ k(T −aI)(xn −xm )k2 +b2 kxn −xm k2 = k(T −λI)(xn −xm )k2 → 0.
Por ser H de Hilbert, existe x = lı́mn xn . De este modo, por ser T − λI
cerrado, debe ser x ∈ D(T − λI) y (T − λI)x = y, es decir y ∈ R(T −
λI).
Por último, para probar d) suponemos que existe un operador simétrico S
tal que T ⊂ S. Entonces H = R(T − λI) ⊂ R(S − λI). Si consideramos
un elemento u ∈ D(S) \ D(T ), aplicando el resultado de b) al operador S,
tenemos:
∃u0 ∈ D(T ) : (S − λI)u = (T − λI)u0 = (S − λI)u0 =⇒ u = u0
lo que es absurdo a no ser que T = S.
♦
El siguiente resultado permite asociar a todo operador cerrado un operador
positivo acotado y sirve de base para dar una prueba del teorema espectral
de operadores autoadjuntos no acotados.
1.13.- Teorema. Sea T cerrado con dominio denso; se define Q = I + T ∗ T .
Entonces:
a) Q : D(Q) → H es biyectivo y existen B, C ∈ L(H), con kBk ≤ 1,
kCk ≤ 1, tales que C = T B y BQ ⊂ QB = I. Además B ≥ 0 y T ∗ T es
autoadjunto.
b) Sea T 0 = T |D(T ∗ T ) ; entonces G(T 0 ) es denso en G(T ).
Demostración. Por el apartado 6 del corolario 1.9 y teniendo en cuenta que T
es cerrado, H × H = G(T ∗ ) ⊕ U G(T ). Entonces, ∀h ∈ H, existen x ∈ D(T ),
y ∈ D(T ∗ ) tales que:
(0, h) = (y, T ∗ y) + U (x, T x) = (y + iT x, T ∗ y − ix).
298
Quedan definidos ası́ los operadores Bh = −ix, Ch = y, que tienen dominio
H y son lineales. Además, debido a que la suma anterior es ortogonal, por
la definición de norma en H × H, tenemos:
khk2 = kChk2 + kT ∗ Chk2 + kT Bhk2 + kBhk2 ≥ kChk2 + kBhk2 .
Entonces kChk ≤ khk y kBhk ≤ khk, con lo que kBk ≤ 1 y kCk ≤ 1.
Además,
0 = Ch − T Bh =⇒ T B = C
h = T ∗ Ch + Bh = Bh + T ∗ T Bh = (I + T ∗ T )Bh =⇒ QB = I.
En particular, ∀y ∈ D(Q), ∃h ∈ H tal que y = Bh; por tanto, Qy = QBh =
h y BQy = Bh = y, de donde BQ ⊂ I.
La aplicación Q es biyectiva pues, por ser QB = I, Q es sobre y, por ser
BQ ⊂ I, Q es inyectiva.
Además, Q es un operador positivo pues, ∀x ∈ D(Q),
hQx, xi = hx, xi + hT ∗ T x, xi = kxk2 + kT xk2 ≥ 0.
Veamos, como consecuencia de lo anterior, que B ≥ 0:
Dado cualquier h ∈ H, sea x ∈ D(Q) tal que h = Qx; entonces
hBh, hi = hBQx, Qxi = hx, Qxi ≥ 0.
Como B ∈ L(H), B es autoadjunto. De 1.10(b) se deduce que Q es también
autoadjunto, con lo que evidentemente Q − I = T ∗ T es autoadjunto.
Para probar b), consideremos un elemento (x, T x) ortogonal a G(T 0 ). Entonces ∀y ∈ D(T ∗ T ) = D(Q) :
0 = h(x, T x), (y, T y)i = hx, yi+hT x, T yi = hx, (I+T ∗ T )yi = hx, Qyi =⇒ x⊥R(Q).
Como R(Q) = H, x = 0.
♦
TT∗
T ∗∗ T ∗
Observación. Teniendo en cuenta que
=
(pues T es cerrado)
∗
y T es cerrado, el resultado anterior también se aplica al operador T T ∗ .
Además, de la proposición 1.10 se deduce que los operadores (I + T ∗ T )−1 y
(I + T T ∗ )−1 son acotados.
Veremos en los ejercicios al final del capı́tulo algunas aplicaciones de este
teorema.
299
2. PROPIEDADES ESPECTRALES DE OPERADORES SIMÉTRICOS Y AUTOADJUNTOS.
Muchas de las propiedades espectrales de operadores autoadjuntos acotados se conservan en el caso de operadores no acotados. Algunas de dichas
propiedades se generalizan en esta sección.
Observemos en primer lugar que, si T : D(T ) ⊂ H → H es un operador lineal
cerrado con dominio denso, entonces T − λI : D(T ) → R(T ) es biyectiva si
y sólo si λ no es autovalor de T . Ası́ pues, los autovalores son aquellos para
los que, o bien T − λI no tiene inverso, o bien (T − λI)−1 no es un operador
acotado definido en todo H.
Si T es además un operador simétrico, sus autovalores son reales (teorema
1.12.b). Esto da lugar al siguiente resultado.
2.1.- Proposición. Sea T un operador autoadjunto. La condición necesaria
y suficiente para que λ sea autovalor de T es que R(T − λI) 6= H.
Demostración. Si λ es autovalor, existe x 6= 0 tal que T x = λx. Entonces:
hx, (T − λI)yi = h(T − λI)x, yi = 0, ∀y ∈ D(T ).
Esto implica que x⊥R(T − λI) con lo que R(T − λI) 6= H.
Recı́procamente, si R(T − λI) 6= H, entonces ∃x 6= 0 tal que x⊥R(T − λI).
Luego
hx, (T − λI)yi = 0, ∀y ∈ D(T )
=⇒ hx, T yi = hx, λyi, ∀y ∈ D(T ) =⇒ x ∈ D(T ∗ ), T ∗ x = λx.
Como T es autoadjunto y λ ∈ R, entonces T x = λx.
♦
2.2.- Corolario. Si T es autoadjunto, el autoespacio correspondiente a un
autovalor λ es R(T − λI)⊥ .
El siguiente resultado es también similar al correspondiente en el caso de
operadores acotados.
2.3.- Teorema. Sea T : D(T ) ⊂ H → H un operador autoadjunto con
dominio denso en H. Entonces
λ ∈ ρ(T ) ⇐⇒ ∃c > 0 : k(T − λI)xk ≥ ckxk, ∀x ∈ D(T ).
Los tres lemas siguientes serán útiles en la determinación del espectro de
los operadores simétricos.
2.4.- Lema. Sea T un operador simétrico cerrado y λ = a + ib un complejo,
con b 6= 0. Si µ ∈ C es tal que |λ − µ| < |b|, entonces N (T ∗ − µI) ∩ N (T ∗ −
λI)⊥ = {0}.
300
Demostración. Supongamos por el contrario que
∃f ∈ N (T ∗ − µI) ∩ N (T ∗ − λI)⊥
y kf k = 1. Como R(T − λI) es cerrado, N (T ∗ − λI)⊥ = R(T − λI), de
modo que existe g ∈ H tal que (T − λI)g = f . Ası́ pues, como f ∈ N (T ∗ −
µI),
0 = h(T ∗ − µI)f, gi = hf, (T − µI)gi
= hf, (T − λI)gi + (λ − µ)hf, gi = kf k2 + (λ − µ)hf, gi.
Entonces
1 = kf k2 = |λ − µ| · |hf, gi| ≤ |λ − µ| · kgk
=⇒ 1 ≤ |λ − µ| · |b|−1 ,
1 = kf k = k(T − λI)gk ≥ |b| · kgk
lo que contradice la hipótesis.
♦
2.5.- Lema. Sean M y N subespacios cerrados de un espacio de Hilbert H,
tales que M ∩ N ⊥ = {0}. Entonces dim M ≤ dim N .
Demostración. Llamamos P : H → H a la proyección ortogonal sobre N y
T : M → N a la restricción de P a M , T f = P f , ∀f ∈ M . Es evidente que T
es inyectiva. Por tanto, si L ⊂ M es un subespacio arbitrario con dim L = k,
entonces dim T L = k ≤ dim N , lo que implica que dim M ≤ dim N . ♦
2.6.- Lema. Si T es un operador simétrico cerrado, entonces dim N (T ∗ −λI)
es constante para cualquier λ con Im λ > 0.
Demostración. De los lemas anteriores, haciendo λ = a + ib, con b > 0, se
deduce que dim N (T ∗ − µI) ≤ dim N (T ∗ − λI) si |λ − µ| < b. Tomando
|λ − µ| < b/2, también |λ − µ| < Im µ, de modo que la desigualdad contraria
también es cierta.
Se prueba ası́ que la función λ 7→ dim N (T ∗ − λI) es localmente constante.
Cubriendo el semiplano superior con bolas donde se cumpla lo anterior, se
obtiene la tesis.
♦
2.7.- Teorema. Si T es un operador simétrico cerrado, entonces una y sólo
una de las siguientes posibilidades es cierta:
i) σ(T ) = C.
ii) σ(T ) = {λ ∈ C : Im λ ≥ 0}.
iii) σ(T ) = {λ ∈ C : Im λ ≤ 0}.
iv) σ(T ) ⊂ R.
Demostración. Sea H± = {λ ∈ C : ± Im λ > 0}. Por la proposición 1.12, si
λ ∈ H± , T − λI es inyectiva y tiene rango cerrado. Tenemos dos posibilidades:
301
- Si T − λI no es sobre, entonces λ ∈ σ(T ).
- Si T − λI es sobre, por la proposición 1.10(d), λ ∈ ρ(T ).
Como N (T ∗ − λI) = R(T − λI)⊥ , del lema anterior resultan las siguientes
opciones (observando además que σ(T ) es cerrado, lo que se prueba como
en el caso de operadores acotados):
i) H+ ⊂ σ(T ), H− ⊂ σ(T ) =⇒ σ(T ) = C.
ii) H+ ⊂ σ(T ), H− ∩ σ(T ) = ∅ =⇒ σ(T ) = H+ = {λ ∈ C : Im λ ≥ 0}.
iii) H+ ∩σ(T ) = ∅, H− ⊂ σ(T ) =⇒ σ(T ) = H− = {λ ∈ C : Im λ ≤ 0}.
iv) H+ ∩ σ(T ) = ∅, H− ∩ σ(T ) = ∅ =⇒ σ(T ) ⊂ R.
♦
2.8.- Proposición. Si T es un operador simétrico cerrado, son equivalentes:
i) T es autoadjunto.
ii) σ(T ) ⊂ R.
iii) N (T ∗ − iI) = N (T ∗ + iI) = {0}.
Demostración. Por ser T simétrico, sus autovalores son reales.
i) =⇒ ii): Sea T autoadjunto y tomemos λ ∈ C \ R. Teniendo en cuenta los
apartados b) y c) del teorema 1.12,
{0} = N (T − λI) = N (T ∗ − λI) = [R(T − λI)]⊥ =⇒ R(T − λI) = H
y, por el teorema anterior (repitiendo el argumento para λ), se deduce que
el espectro de T es real.
ii) =⇒ iii): Como ±i ∈ ρ(T ),
N (T ∗ ± iI) = [R(T ∓ iI)]⊥ = H ⊥ = {0}.
iii) =⇒ i): Por hipótesis, R(T − iI) = R(T + iI) = H. Veamos que además
T ± iI son inyectivas:
Sea x ∈ D(T ) tal que (T ± iI)x = 0. Por ser T ∗ extensión de T , ∀z ∈ H
resulta:
hx, zi = hx, (T ∓iI)yi = h(T ∗ ±iI)x, yi = h(T ±iI)x, yi = h0, yi = 0 =⇒ x = 0.
Esto quiere decir que existe (T ± iI)−1 ∈ L(H). Como [(T ± iI)−1 ]∗ =
(T ∗ ∓ iI)−1 , también (T ∗ ∓ iI)−1 ∈ L(H).
Sea h ∈ D(T ∗ ). Entonces existe f ∈ D(T ) tal que (T + iI)f = (T ∗ + iI)h.
Pero (T + iI)f = (T ∗ + iI)f , de modo que f = h y T = T ∗ .
♦
302
3. TEOREMA ESPECTRAL DE OPERADORES UNITARIOS.
A fin de lograr una representación espectral de operadores autoadjuntos,
utilizaremos la transformada de Cayley y la representación espectral de
operadores unitarios, que son acotados. En esta sección se deduce dicha
representación espectral. Utilizaremos el enfoque clásico, inigualable en su
alcance al enfoque actual vı́a la teorı́a de álgebras de Banach, transformada de Gelfand y teorema de Gelfand-Naimark, pero más próximo a quienes
estén orientados a las aplicaciones.
En primer lugar se prueba que el espectro de un operador unitario está en
la circunferencia unidad.
3.1.- Teorema. Sea U : H → H un operador unitario en un espacio de
Hilbert complejo H; entonces |λ| = 1, ∀λ ∈ σ(U ).
Demostración. Basta observar que,
si |λ| < 1,
k(U − λI)xk ≥ kU xk − |λ| · kxk = (1 − |λ|)kxk,
si |λ| > 1,
k(U − λI)xk ≥ |λ| · kxk − kU xk = (|λ| − 1)kxk,
y, en ambos casos, ∃(U − λI)−1 ∈ L(H).
♦
Hay varias formas de obtener el teorema espectral de operadores unitarios,
desde la de Wintner (1929) y pasando por las de von Neumann (1930), Stone
(1932), Wecken (1935), Friedrichs (1935) y Riesz-Nagy (1955).
En el caso finito-dimensional sabemos que si H es un espacio de Hilbert
con dim H = n y U es un operador unitario en H, entonces existe una
base ortonormal {v1 , . . . , vn } de H formada por vectores propios de U , con
U vj = λj vj , j = 1, . . . , n y |λj | = 1. Si llamamos Ej al subespacio propio
asociado a λj ,
Ej = {v ∈ H : U v = λj v},
y Pj a la proyección ortogonal de H sobre Ej (j = 1, . . . , m con m ≤ n), el
teorema espectral dice que
i) H = E1 ⊕ · · · ⊕ Em ;
ii) I = P1 + . . . Pm ;
iii) U = λ1 P1 + · · · + λm Pm .
Una posible generalización
en dimensión
R infinita puede producir la descomP
posición U = ∞
λ
P
o
bien
U
=
λdP , siendo T = {λ ∈ C : |λ| = 1}
k
k
k=1
T
(pues los autovalores están en la circunferencia unidad).
303
Para que tenga sentido dicha integral necesitamos definir una correspondencia entre la σ-álgebra Ω de subconjuntos de Borel en T y el espacio L(H) de
los operadores lineales y acotados en H que tenga las propiedades de una
medida. De ahı́ que debamos introducir la siguiente definición.
3.2.- Definición. Sean X un conjunto arbitrario, Ω una σ-álgebra de subconjuntos de X y H un espacio de Hilbert. Una medida espectral u ortogonal en (X, Ω, H) es una correspondencia E : Ω → L(H) con las propiedades
i) E(∆) es una proyección ortogonal, ∀∆ ∈ Ω.
ii) E(X) = I, E(∅) = 0.
iii) Si {A
Sn }n∈N ⊂ ΩPson disjuntos dos a dos y x ∈ H arbitrario, entonces
E(
An )x =
E(An )x.
n∈N
n∈N
iv) E(A ∩ B) = E(A)E(B), ∀A, B ∈ Ω.
De la definición se deduce inmediatamente el siguiente resultado.
3.3.- Lema. Si E es una medida espectral en (X, Ω, H) y x, y ∈ H, entonces
la función de conjuntos Ex,y : Ω → C definida por Ex,y (∆) = hE(∆)x, yi
es una medida numerablemente aditiva en Ω con variación total kEx,y k ≤
kxk · kyk.
El siguiente resultado da sentido al concepto de integral respecto a una
medida espectral.
3.4.- Proposición. Si E es una medida espectral en (X, Ω, H) y φ : X → C
una función Ω-medible acotada, existe un único operador A ∈ L(H) tal que
para cualesquiera ε > 0 y {∆1 , . . . , ∆n } Ω-partición de X con
sup{|φ(x) − φ(x0 )| : x, x0 ∈ ∆k } < ε (1 ≤ k ≤ n),
entonces
n
X
φ(xk )E(∆k ) < ε, ∀xk ∈ ∆k .
A −
k=1
RDicho operador se llama integral de φ respecto a E y se
R denota por A =
X φdE. Del resultado anterior se deduce que hAx, yi = X φdEx,y .
Pn
Demostración.
PnA cada función simple s = k=1 αk χ∆k le asociamos el operador As = k=1 αk E(∆k ).
Como cada E(∆k ) es autoadjunto, entonces
A∗s =
n
X
αk E(∆k ) = A s .
k=1
304
Si t =
Pm
j=1 βj χ∆0j
As At =
X
es otra función simple, entonces
αk βj E(∆k )E(∆0j ) =
k,j
X
αk βj E(∆k ∩ ∆0j ) = Ast .
k,j
De estas igualdades se deduce que
A∗s As = A s As = A ss = A|s|2 .
Si tomamos x, y ∈ H arbitrarios, obtenemos:
hAs x, yi =
n
X
αk hE(∆k )x, yi =
k=1
n
X
Z
sdEx,y ,
αk Ex,y (∆k ) =
k=1
X
de modo que
2
kAs xk =
hA∗s As x, xi
Z
= hA|s|2 x, xi =
|s|2 dEx,x ≤ ksk2∞ kEx,x k ≤ ksk2∞ ·kxk2 ,
X
es decir kAs xk ≤ ksk∞ · kxk.
Por otra parte, es claro que, si x ∈ R(E(∆i )), entonces As x = αi E(∆i )x =
αi x; de esta igualdad y eligiendo i de manera que |αi | = ksk∞ , resulta
que
(∗)
kAs k = ksk∞ .
Sea ahora φ : X → C una función Ω-medible y acotada y (s(i) )i∈N una sucesión de funciones simples medibles que converge a φ. De la fórmula (∗)
deducimos que la sucesión (As(i) )i∈N es de Cauchy en L(H); por tanto, converge a un operador A ∈ L(H). Dicho operador no depende de la elección
de la sucesión (s(i) )i∈N . Ası́ pues, dados ε > 0 y {∆1 , . . . , ∆n } con las condiciones indicadas en el enunciado, la tesis se sigue de la convergencia de la
sucesión (As(i) )i∈N al operador A.
♦
Con esta notación, si consideramos la σ-álgebra
Ω = {∆ ⊂ T : ∆ de Borel en T},
el teorema espectral se enuncia entonces de la siguiente forma:
3.5.- Teorema. Si U ∈ L(H) es unitario,
R nentonces existe una única medida
n
espectral E en (T, Ω, H) tal que U = T z dE(z), ∀n ∈ Z.
Observación. Debido a que todo punto z ∈ T
puede representarse como
R 2π
z = eit , con t ∈ [0, 2π), podemos escribir U n = 0 eint dE(t).
Demostración. El proceso será el siguiente:
305
1) Buscaremos una familia de medidas {µx , x ∈ H} tal que
Z
hU n x, xi = z n dµx (z), ∀n ∈ Z.
T
Fijado x ∈ H, consideramos la sucesión numérica {cn (x)}n∈Z , definida por
cn (x) = hU n x, xi. De la definición es claro que c−n = cn .
R
Como la medida espectral
debe verificar que U n = T z n dE(z), ∀n ∈ Z y, en
R
particular, hU n x, xi = T z n dhE(z)x, xi, ∀x ∈ H, la medida escalar
R n positiva µx definida por µx (∆) = hE(∆)x, xi debe verificar cn (x) = T z dµx (z),
∀n ∈ Z. La existencia de tal medida corresponde al llamado problema trigonométrico de momentos; la respuesta a dicho problema la proporciona el
teorema de representación de Herglotz:
Dicha medida µ existe (y es única) si y sólo si la sucesión {cn }n∈Z es definida
positiva, es decir
N
X
cj−k λj λk ≥ 0, ∀N ∈ N, ∀λ1 , . . . , λN ∈ C.
j,k=1
En este caso la sucesión {hU n x, xi}n∈Z es definida positiva, pues
N
X
cj−k (x)λj λk =
j,k=1
N
X
hU j−k x, xiλj λk
j,k=1
=
N
X
N
X
2
hλj U x, λk U xi = λj U j x ≥ 0.
j
k
j=1
j,k=1
2) A continuación queremos
encontrar una familia de medidas µx,y (∆) para
R n
n
las que hU x, yi = T z dµx,y (z), ∀n ∈ Z.
Para ello utilizamos la identidad de polarización
hU n x, yi =
1
[hU n (x + y), x + yi − hU n (x − y), x − yi]
4
i
+ [hU n (x + iy), x + iyi − hU n (x − iy), x − iyi] ,
4
por lo que basta definir
1
1
i
i
µx,y (∆) = µx+y (∆) − µx−y (∆) + µx+iy (∆) − µx−iy (∆).
4
4
4
4
3) Fijado ∆ de Borel en T, la función β(∆) : H × H → C definida por
306
β(∆)(x, y) = µx,y (∆) es una forma sesquilineal:
Z
z n dµαx1 +x2 ,y (z),
Z
Z
n
n
n
αhU x1 , yi + hU x2 , yi = α z dµx1 ,y (z) + z n dµx2 ,y (z)
T
Z T
z n d[αµx1 ,y (z) + µx2 ,y (z)],
=
n
hU (αx1 + x2 ), yi =
T
T
de modo que
Z
Z
f (z)d[αµx1 ,y (z) + µx2 ,y (z)],
f (z)dµαx1 +x2 ,y (z) =
T
T
∀f exponencial trigonométrica. Por linealidad, también es cierta para polinomios trigonométricos y, por el teorema de aproximación de Weierstrass,
también para toda función continua o continua a trozos. En particular,
Z
Z
χ∆ (z)dµαx1 +x2 ,y (z) =
T
χ∆ (z)d[αµx1 ,y (z) + µx2 ,y (z)],
T
o bien µαx1 +x2 ,y (∆) = αµx1 ,y (∆) + µx2 ,y (∆).
Análogamente, debido a la igualdad
n
x, yi = z −n dµx,y (z)
Z T
hU n y, xi = z −n d µy,x (z), ∀n ∈ Z,
hx, U yi = hU
=
Z
−n
T
y razonando como en el caso anterior, se deduce que µx,y (∆) = µy,x (∆).
4) Veremos a continuación que F : C(T) → L(H), definida por F (g) = g(U ),
es una representación de C(T) (espacio de las funciones continuas en T con
la norma del supremo), es decir es un homomorfismo de álgebras que cumple
F (g ∗ ) = F (g)∗ , donde definimos g ∗ (x) = g(x).
Definimos en primer lugar F : P P
→ L(H) por F (p) = p(U ), donde denotan
2
mos por P = {p : T → C : p(z) = N
n=N1 an z } al espacio de los polinomios
trigonométricos con la norma del supremo. Resultan de la definición las
siguientes propiedades:
i) F es lineal, F (α1 p1 + α2 p2 ) = α1 F (p1 ) + α2 F (p2 ).
ii) F es multiplicativa, F (p1 p2 ) = F (p1 )F (p2 ).
R
iii) hp(U )x, yi = T p(z)dµx,y (z), ∀x, y ∈ H.
307
iv) p(U ) = p(U )∗ :
Z
∗
Z
hx, p(U ) yi = hp(U )x, yi = p(z)dµx,y (z) =
p(z)d µx,y (z)
T
T
Z
=
p(z)dµy,x (z) = h p(U )y, xi = hx, p(U )yi.
T
v) Si p(z) ≥ 0, ∀z, entonces p(U ) ≥ 0:
Por el teorema de Fejér-Riesz, si p ∈ P es positivo, ∃q ∈ P : p = |q|2 .
Entonces
hp(U )x, xi = h( qq)(U )x, xi = h q(U )q(U )x, xi = hq(U )∗ q(U )x, xi = kq(U )xk2 ≥ 0.
vi) kF k = 1:
kp(U )xk2 = hp(U )x, p(U )xi = hp(U )∗ p(U )x, xi ≤ kpk2∞ · kxk2
⇐⇒
h[kpk2∞ I − p(U )∗ p(U )]x, xi ≥ 0.
Como kpk2∞ I − p(U )∗ p(U ) = F (q) con q(z) = kpk2∞ − |p(z)|2 ≥ 0, la desigualdad anterior se deduce de v). En definitiva,
kp(U )xk ≤ kpk∞ · kxk =⇒ kp(U )k ≤ kpk∞ =⇒ kF k ≤ 1.
Por otra parte, tomando p(z) = 1, ∀z, entonces p(U ) = I de modo que
kF k ≥ kp(U )k/kpk∞ = 1 =⇒ kF k = 1.
Como F es acotada y L(H) es completo, F se extiende a P que es el espacio C(T) de las funciones continuas con la norma del supremo, donde se
mantienen las propiedades anteriores; en particular,
Z
(∗)
hF (g)x, yi = hg(U )x, yi = g(z)dµx,y (z), ∀g ∈ C(T).
T
5) Debido a la equivalencia entre el dual de C(T) y el espacio
de las medidas
R
de Borel finitas en T, dada por µ 7→ l ∈ C(T)0 , con l(f ) = T f dµ, ∀f ∈ C(T),
podemos probar la acotación de µx,y como sigue:
Z
kµx,y k = sup f dµx,y : f ∈ C(T), kf k∞ ≤ 1
T
= sup{|hf (U )x, yi| : f ∈ C(T), kf k∞ ≤ 1}
≤ sup{kf (U )k · kxk · kyk : f ∈ C(T), kf k ≤ 1} ≤ kxk · kyk.
6) El siguiente paso es extender la representación F a la C ∗ -álgebra B(T)
de las funciones medibles Borel y acotadas en T.
308
R
Fijamos ahora g ∈ B(T) y definimos βg (x, y) = T g(z)dµx,y (z). Debido a
que βg es un forma sesquilineal acotada con kβg k ≤ kgk∞ , por el teorema
de representación de Riesz para formas sesquilineales (capı́tulo III, teorema
6.5), existe un único operador Ag ∈ L(H) tal que βg (x, y) = hAg x, yi y
kAg k ≤ kgk∞ . La nueva aplicación F : B(T) → L(H) definida por F (g) =
Ag está bien definida, kF (g)k ≤ kgk∞ y
Z
(∗∗)
hF (g)x, yi = g(z)dµx,y (z), ∀x, y ∈ H.
T
Debemos probar a continuación que F es una representación de B(T) que
extiende a la correspondiente representación de C(T).
i) Es inmediato de (∗) y (∗∗) que se trata de una extensión.
ii) Es también evidente que F es lineal y tiene norma 1.
iii) F ( g) = F (g)∗ pues, ∀x, y ∈ H:
∗
hF (g) x, yi =
hA∗g x, yi
Z
= hAg y, xi =
g(z)dµy,x (z)
T
Z
g(z)dµx,y (z) = hA g x, yi = hF ( g)x, yi.
=
T
iv) F es multiplicativa; para ello veamos en primer lugar que F (f g) =
F (f )F (g) con f ∈ C(T) y g ∈ B(T), pero debido a las equivalencias
F (f g) = F (f )F (g) ⇐⇒ hF (f g)x, yi = hF (f )F (g)x, yi = hF (g)x, F (f )∗ yi
Z
Z
⇐⇒
(f g)(z)dµx,y (z) = g(z)dµx,F (f )∗ y (z),
T
T
la igualdad
anterior será
R
R cierta si y sólo si f dµx,y = dµx,F (f )∗ y , ∀f ∈ C(T),
o bien T ϕf dµx,y = T ϕdµx,F (f )∗ y , ∀ϕ ∈ C(T), lo que equivale a la multiplicatividad de F en C(T) que ya fue probada.
R
R
Queda ası́ probado que T f (z)(g(z)dµx,y (z)) = T f (z)dµx,g(U )∗ y (z), ∀f ∈
C(T), g ∈ B(T), de donde gdµx,y = dµx,g(U )∗ y .
Sean ahora g, g1 ∈ B(T); entonces
Z
Z
hF (gg1 )x, yi =
(gg1 )(z)dµx,y (z) = g1 (z)dµx,g(U )∗ y (z)
T
T
= hg1 (U )x, g(U )∗ yi = hg(U )g1 (U )x, yi = hF (g)F (g1 )x, yi.
7) Definimos ahora, para cada ∆ de Borel en T el operador
E(∆) = F (χ∆ ) ∈ L(H).
De la definición se deduce directamente que hE(∆)x, yi = µx,y (∆). Veamos
que E es una medida espectral en T.
309
i) E(∆) es un proyector ortogonal:
E(∆)2 = F (χ∆ ) · F (χ∆ ) = F (χ∆ · χ∆ ) = F (χ∆ ) = E(∆);
E(∆)∗ = F (χ∆ )∗ = F ( χ∆ ) = F (χ∆ ) = E(∆).
ii) E(T) = F (χT ) = F (1) = I, E(∅) = F (χ∅ ) = F (0) = 0.
iii) Si ∆1 , ∆2 ∈ Ω,
E(∆1 ∩∆2 ) = F (χ∆1 ∩∆2 ) = F (χ∆1 χ∆2 ) = F (χ∆1 )F (χ∆2 ) = E(∆1 )E(∆2 ).
iv) Si {∆j }j∈N ⊂ Ω son disjuntos
S dos a dos, es fácil probar la aditividad
finita. Si llamamos Hn = k>n ∆k , para todo x ∈ H tenemos:
m
[
2
X
∆j )x −
E(∆j )x = E(Hm )x, E(Hm )x
E(
j∈N
j=1
E(Hm )x, x = F (χHm )x, x
Z
X
=
χHm (z)dµx,x (z) =
µx,x (∆j ),
=
T
j>m
expresión que tiende a cero si m → ∞.
R
8) Por último veamos que F (g) = T g(z)dE(z), ∀g ∈ C(T):
Dado ε > 0, sea {∆1 , . . . , ∆n } una partición de T mediante elementos de Ω
tal que
sup{|g(x) − g(x0 )| : x, x0 ∈ ∆k } < ε, (1 ≤ k ≤ n).
P
Entonces, para cualquierPelección xk ∈ ∆k , kg − nk=1 g(xk )χ∆k k∞ < ε.
Como
kF k = 1, kF (g) − nk=1 g(xk )E(∆k )k < ε, lo que implica que F (g) =
R
g(z)dE(z), ∀g ∈ C(T).
T
R
En particular, si g(z) = z n , entonces F (g) = U n , de donde U n = T z n dE(z),
lo que completa la demostración.
♦
La medida espectral encontrada tiene la siguiente propiedad adicional.
3.6.- Proposición. Si U ∈ L(H) es un operador unitario y A ∈ L(H) es
un operador que conmuta con U , entonces A conmuta con E(∆), para todo
∆ de Borel en T. Además µx,A∗ y = µAx,y .
Demostración. En primer lugar se comprueba que Ap(U ) = p(U )A, para
cualquier polinomio trigonométrico p. A continuación, si aproximamos toda
función continua f ∈ C(T) mediante polinomios trigonométricos (aplicando el teorema de Stone-Weierstrass), se prueba que Af (U ) = f (U )A. Por
último, si ∆ ∈ Ω, consideremos la sucesión creciente {gn }n∈N de funciones
310
continuas tal que gn → χ∆ . Por el teorema de la convergencia monótona,
∀x, y ∈ H se tiene:
hAE(∆)x, yi = hE(∆)x, A∗ yi = µx,A∗ y (∆)
Z
Z
=
χ∆ (z)dµx,A∗ y (z) = lı́m gn (z)dµx,A∗ y (z) = lı́mhgn (U )x, A∗ yi
n
T
T
n
= lı́mhAgn (U )x, yi = lı́mhgn (U )Ax, yi = hE(∆)Ax, yi.
n
n
Para la segunda parte, de AU = U A se deduce que:
hE(∆)Ax, yi = hAE(∆)x, yi = hE(∆)x, A∗ yi =⇒ µx,A∗ y = µAx,y .
♦
4. TEOREMA ESPECTRAL DE OPERADORES AUTOADJUNTOS NO ACOTADOS.
Es natural preguntarse si existe una descomposición espectral de todo operador simétrico análoga a la que existe en el caso de operadores acotados.
Trabajos importantes, especialmente de Carleman relativos a ecuaciones
integrales singulares, mostraron la imposibilidad de obtener una completa analogı́a. Fue E. Schmidt quien observó que es necesario restringirse a
operadores autoadjuntos si se quiere obtener una descomposición análoga.
El teorema espectral para operadores autoadjuntos fue probado de diferentes maneras por von Neumann, Stone, Riesz y otros y constituyó el punto
de partida de la nueva teorı́a de operadores lineales en espacios de Hilbert.
En esta sección ilustramos una demostración de von Neumann que hace uso
de la transformada de Cayley y, por tanto, se basa en la descomposición
espectral de operadores unitarios (acotados). Otras demostraciones pueden
verse en los distintos textos de Análisis Funcional (ver por ejemplo [BN],
[RN], [Fu], [Ru]).
Si uno considera los operadores, acotados o no, en espacios de Hilbert como
generalizaciones de los números complejos, se encuentra que muchos resultados sencillos en relación a los números complejos tienen análogos no triviales
en el contexto de operadores. Uno de ellos se refiere a la transformada de
Möbius. Si en el espacio C definimos el conjunto T = {z ∈ C : |z| = 1},
la transformación de Möbius w = z−i
z+i es una aplicación biyectiva de R en
T \ {1} cuya inversa es z =
i(1+w)
1−w .
Una adaptación de esta transformación al caso de operadores permitirá aplicar operadores autoadjuntos no
311
acotados sobre operadores unitarios acotados y operadores simétricos sobre
isométricos. Esto permitirá establecer una analogı́a entre operadores lineales
y números complejos. Mediante esta analogı́a los operadores autoadjuntos
jugarán el papel de números reales, los operadores positivos corresponderán
a los reales no negativos y los operadores unitarios a los complejos de módulo 1. Esto viene sugerido por el hecho de que el espectro de un operador
autoadjunto es real y el de un operador unitario está contenido en T. El paralelismo es más acusado si tenemos en cuenta que T es autoadjunto en un
espacio complejo si y sólo si hT x, xi ∈ R, ∀x. El siguiente ejemplo muestra
que lo anterior no es cierto si el espacio es real:
En el espacio X = R2 definimos el operador T (x1 , x2 ) = (x1 + 2x2 , x2 ).
Entonces hT x, xi = 2|x2 | ∈ R pero T ∗ (x1 , x2 ) = (x1 , 2x1 + x2 ).
La relación entre operadores autoadjuntos y unitarios viene dada por el
siguiente resultado.
4.1.- Proposición. Sea T un operador autoadjunto en H. Entonces los
operadores T ± iI tienen inversas acotadas definidas en todo H y el operador
U = (T − iI)(T + iI)−1
es un operador unitario en H, llamado transformada de Cayley de T .
Demostración. La primera parte se deduce de los teoremas 1.10 y 1.12 y de
las igualdades N (T ± iI) = R(T ∓ iI)⊥ .
Para ver que U es unitario, sea x ∈ H y llamamos y = (T + iI)−1 x. Entonces:
kU xk2 = h(T − iI)y, (T − iI)yi = hT y, T yi − ihy, T yi + ihT y, yi + hy, yi
= hT y, T yi − ihT y, yi + ihy, T yi + hy, yi
= h(T + iI)y, (T + iI)yi = kxk2 .
♦
Recı́procamente, conocida la transformada de Cayley de un operador autoadjunto, se puede extraer este como sigue.
4.2.- Proposición. Si U es la transformada de Cayley de un operador autoadjunto T en H, entonces I − U es inyectiva y T = i(I + U )(I − U )−1 .
Demostración. Si (I − U )x = 0 y llamamos y = (T + iI)−1 x, tenemos:
x = U x =⇒ x = (T − iI)y =⇒ (T + iI)y = (T − iI)y =⇒ y = 0 =⇒ x = 0.
La segunda parte se obtiene por cálculo directo.
♦
4.3.- Corolario. Sea U la transformada de Cayley de un operador autoadjunto T . Entonces 1 no es autovalor de U . Además 1 está en la resolvente
de U si y sólo si T es acotado.
312
El recı́proco del resultado anterior también es cierto: si 1 no es autovalor de
un operador unitario U , entonces U es la transformada de Cayley de algún
operador autoadjunto.
Los dos últimos teoremas, con los que concluimos el capı́tulo y el curso,
permiten establecer una correspondencia biunı́voca entre las medidas espectrales en R y los operadores autoadjuntos.
4.4.- Teorema (espectral de operadores autoadjuntos.) Sea T : D(T ) →
H un operador autoadjunto con dominio
R denso en H. Entonces existe una
medida espectral P en R tal que T = R λdP (λ).
Demostración. Sea U = (T − iI)(T + iI)−1 la transformada de Cayley de T ;
como ya se ha probado, U es unitario, I − U es inyectivo y T = i(I + U )(I −
U )−1 con D(T ) = (I − U )(H).
Por el teorema espectral
de operadores unitarios, existe E medida espectral
R
en T tal que U = T zdE(z).
Por ser I − U inyectivo, 1 no es valor propio de U . De aquı́ se deduce que
E({1}) = 0.
En efecto, supongamos por el contrario que H0 = E({1})H 6= {0}. Entonces
existe x 6= 0 tal que x = E({1})x de donde U x = U E({1})x. Como E({1})
es el operador asociado a la función caracterı́stica χ{1} , tenemos:
Z
λ · χ{1} (λ)dE(λ)x = 1 · E({1})x = x,
U x = U E({1})x =
T
lo cual contradice que I − U es inyectivo.
1+z
Como la función ϕ : T \ {1} → R definida por ϕ(z) = i · 1−z
es biyectiva, la
−1
función P (∆) = E(ϕ (∆)), ∀∆ de Borel en R, es una medida espectral en
R (como E({1}) = 0, E(T) = E(T \ {1}) = I).
Debido a la fórmula de la transformada de Cayley, procediendo formalmente,
obtenemos:
Z
Z
1+z
T = i(I + U )(I − U )−1 = i ·
dE(z) = ϕ(z)dE(z);
1−z
T
T
si hacemos el cambio λ = ϕ(z), resulta
Z
∞
T =
λdE(ϕ−1 (λ)) =
−∞
Z
∞
λdP (λ).
♦
−∞
R∞
Veamos el sentido de la expresión −∞ f (λ)dP (λ), con f : R → R función
medible, no necesariamente acotada.
313
4.5.- Teorema. Sea P una medida espectral en R y f : R → R una función medible. Existe entonces un único operador autoadjunto T con dominio
Z
f 2 (λ)dhP (λ)x, xi < ∞}
D(T ) = {x ∈ H :
R
tal que T =
R
R
f (λ)dP (λ) y
kT xk2
=
R
R
f 2 (λ)dhP (λ)x, xi, ∀x ∈ D(T ).
Demostración. Haremos la demostración en dos pasos.
R∞
1) Si f es acotada, −∞ f (λ)dP (λ) es un operador acotado simétrico:
R∞
En efecto, la aplicación β(x, y) = −∞ f (λ)dhP (λ)x, yi es un funcional sesquilineal acotado pues
Z ∞
d|hP (λ)x, yi| ≤ kf k∞ · kxk · kyk.
|β(x, y)| ≤ kf k∞
−∞
Por tanto, existe un operador T ∈ L(H) tal que β(x, y) = hT x, yi, ∀x, y ∈ H.
Además T es autoadjunto pues
Z ∞
hx, T yi = hT y, xi = β(y, x) =
f (λ)d hP (λ)y, xi
−∞
Z ∞
=
f (λ)dhP (λ)x, yi = β(x, y) = hT x, yi.
−∞
Escribiremos en este caso T =
R∞
−∞ f (λ)dP (λ).
2) Si S
f es medible, llamamos ∆n = f −1 [n, n + 1), ∀n ∈ Z; por definición,
R = n∈Z ∆n y la unión es disjunta. Si llamamos ahora ϕn = χ∆n , Pn =
P
P
L
P (∆n ) y Hn = Pn H, entonces 1 = n∈Z ϕn , I = n∈Z Pn , H = n∈Z Hn
(donde la suma es ortogonal por ser {Pn }n∈Z una familia ortogonal de proyecciones).
Como ahora f (λ)ϕn (λ) son funciones acotadas para todo n, existen, según
el apartado anterior, Tn0 operadores simétricos y acotados tales que
Z ∞
0
Tn =
f (λ)ϕn (λ)dP (λ).
−∞
Veamos ahora que Tn0 H ⊂ Hn , para lo cual basta probar que Pn Tn0 =
Tn0 :
R
Como Tn0 = ∆n f (λ)dP (λ), podemos aproximarlo por sumas de Riemann
P
del tipo Tn0 ∼ kj=1 f (λj )P (Fj ), siendo {F1 , . . . , Fk } una partición de ∆n y
λj ∈ Fj (j = 1, . . . , k). Entonces
Pn Tn0
∼
k
X
j=1
f (λj )P (∆n )P (Fj ) =
k
X
f (λj )P (∆n ∩ Fj ) =
j=1
314
k
X
j=1
f (λj )P (Fj ).
Como ambas sumas de Riemann coinciden, Tn0 = Pn Tn0 y, en consecuencia,
R(Tn0 ) ⊂ Hn .
Lo anterior permite definir los operadores
Z ∞
Tn =
f (λ)ϕn (λ)dP (λ)|Hn : Hn → Hn
−∞
y probaremos a continuación que existe un único operador autoadjunto T
en H tal que T |Hn = Tn (teorema de Riesz-Lorch):
P
Definimos pues T x = n∈Z Tn Pn x cuyo dominio es
D = {x ∈ H :
X
kTn Pn xk2 < ∞}
n∈Z
(ver teorema 4.7, capı́tulo III). Ası́ x ∈ D si y sólo si
converge cuando k → ∞.
P
n∈[−k,k] Tn Pn x
Ası́ definido se cumplen las siguientes propiedades:
i) D ⊃ Hn , ∀n ∈ Z.
ii) T está bien definido pues, si x ∈ D,
X
X
X
Pn x =
T (Pn x) =
Tn Pn x.
Tx = T
n∈Z
n∈Z
n∈Z
iii) D es denso en H. En efecto, por i),
Hn ⊂ D =⇒ h
[
Hn i ⊂ D =⇒ h
n∈Z
iv) D = {x ∈ H :
kTn Pn xk
2
Hn i ⊂ D =⇒ H =
n∈Z
R∞
−∞ f
Z
2 (λ)dhP (λ)x, xi
f
−∞
X
2
M
Hn ⊂ D.
n∈Z
< ∞} pues
∞
=
=⇒
[
(λ)ϕ2n (λ)dhP (λ)x, xi
Z
=
f 2 (λ)dhP (λ)x, xi
∆n
2
Z
∞
f 2 (λ)dhP (λ)x, xi.
kTn Pn xk =
−∞
n∈Z
v) T es simétrico pues, ∀x, x0 ∈ H,
X
X
hT x, x0 i =
hTn Pn x, x0 i =
hTn Pn x, Pn x0 i
n∈Z
=
X
n∈Z
hPn x, Tn Pn x0 i =
n∈Z
X
n∈Z
315
hx, Tn Pn x0 i = hx, T x0 i.
vi) T es autoadjunto, para lo cual basta probar que D(T ∗ ) ⊂ D(T ).
Sea y ∈ D(T ∗ ); entonces existe y ∗ tal que hT x, yi = hx, y ∗ i, ∀x ∈ D.
Veamos que Pn y ∗ = Tn Pn y:
hTn Pn y, xi = hTn Pn y, Pn xi = hPn y, Tn Pn xi = hy, Tn Pn xi
= hy, T Pn xi = hy ∗ , Pn xi = hPn y ∗ , xi, ∀x ∈ H.
P
P
Entonces n∈Z kTn Pn yk2 = n∈Z kPn y ∗ k2 = ky ∗ k2 < ∞ =⇒ y ∈ D.
vii) T es único. Para ello, supongamos que existe un operador autoadjunto
S tal que S|Hn = Tn , ∀n ∈ N. Veamos que S = T .
Si x ∈ D(T ), debido a que
X
X
kTn Pn xk2 < ∞,
kSPn xk2 =
n∈N
n∈N
P
se deduce que n∈N SPn x converge.
P
Por otro lado, como las sumas parciales de n∈N Pn x (que están en
D(S)) convergen a x y S es cerrado, x ∈ D(S) y además
X
X
Sx =
SPn x =
Tn Pn x = T x.
n∈N
n∈N
Esto implica que T ⊂ S.
Recı́procamente, por ser S autoadjunto, de la proposición 1.4 deducimos que S = S ∗ ⊂ T ∗ = T , de donde S = T .
♦
Observaciones. 1) La forma que adopta la descomposición espectral de un
operador autoadjunto no acotado es similar a la correspondiente del caso
acotado. Sin embargo aquı́ los lı́mites de integración en la representación no
son finitos debido a que el espectro de un operador autoadjunto no acotado,
aun siendo real, no es acotado.
2) De la descomposición espectral de un operador autoadjunto T se puede
obtener también una fórmula para la resolvente Rz = (T −zI)−1 (ver propiedades de la misma en los ejercicios al final del capı́tulo). Más precisamente,
si P es la medida espectral de T ,
Z
1
Rz =
dP (λ)
λ
−
z
R
para cualquier valor de z donde tengan sentido dichas expresiones. Esta
fórmula se puede generalizar a operadores simétricos arbitrarios y proporcionar ası́ diversas aplicaciones de la teorı́a de operadores.
3) Algunas notas históricas con respecto al teorema espectral pueden consultarse en las obras de Steen [Ste], Dunford-Schwartz [DS] y Halmos [Ha1].
316
EJERCICIOS.
1. a) Probar que los operadores M f (x) = xf (x), Df (x) = f 0 (x) definidos en L2 (R) son operadores simétricos no acotados y verifican
la relación de conmutación DM − M D = I .
b) Probar que no existe ningún par de operadores acotados A, B
que cumplan la relación AB − BA = I .
Resp.: a) En diversos lugares se ha probado ya que dichos operadores
son simétricos no acotados. Además
DM f (x) = D(xf (x)) = xf 0 (x) + f (x) = (I + M D)f (x),
es decir DM − M D = I (en esta fórmula se basa el principio de
incertidumbre en Mecánica Cuántica).
b) Supongamos que existen A, B ∈ L(H) tales que AB − BA = I.
Entonces, multiplicando a izquierda y derecha por A, obtenemos:
A2 B − ABA = A
y
ABA − BA2 = A.
Al sumar miembro a miembro, resulta que A2 B − BA2 = 2A.
Repitiendo el proceso, se llega a la igualdad general
An B − BAn = nAn−1 .
Entonces nkAn−1 k ≤ kAn Bk + kBAn k ≤ kAn−1 k · kABk + kBAk ·
kAn−1 k.
Si suponemos que A 6= 0, entonces kAn−1 k =
6 0, ∀n, y de lo anterior
se deduce que n ≤ kABk + kBAk ≤ 2kAk · kBk, lo cual contradice el
hecho de que A y B son operadores acotados.
2. Sean T1 , T2 , T3 tres operadores arbitrarios.
a) Probar que (T1 T2 )T3 = T1 (T2 T3 ).
b) Probar que T1 ⊂ T2 =⇒ T3 T1 ⊂ T3 T2 y T1 T3 ⊂ T2 T3 .
Resp.: a) Veamos en primer lugar que D((T1 T2 )T3 ) = D(T1 (T2 T3 )).
317
En efecto,
x ∈ D((T1 T2 )T3 ) ⇐⇒ x ∈ D(T3 ), T3 x ∈ D(T1 T2 )
⇐⇒ x ∈ D(T3 ), T3 x ∈ D(T2 ), T2 T3 x ∈ D(T1 )
⇐⇒ x ∈ D(T2 T3 ), T2 T3 x ∈ D(T1 ) ⇐⇒ x ∈ D(T1 (T2 T3 )).
Por otra parte, es evidente que, si x ∈ D((T1 T2 )T3 ), entonces (T1 T2 )T3 x =
T1 (T2 T3 )x.
b) Como, por hipótesis, T1 ⊂ T2 , entonces D(T1 ) ⊂ D(T2 ) y T1 x =
T2 x, ∀x ∈ D(T1 ). Resulta ası́:
x ∈ D(T3 T1 ) =⇒ x ∈ D(T1 ), T1 x ∈ D(T3 )
=⇒ x ∈ D(T2 ), T2 x ∈ D(T3 ) =⇒ x ∈ D(T3 T2 ).
Además, ∀x ∈ D(T3 T1 ):
(T3 T1 )x = T3 (T1 x) = T3 (T2 x) = (T3 T2 )x,
lo que prueba que T3 T1 ⊂ T3 T2 .
Con el otro caso se procede de la misma forma.
3. Sea H = L2 (R) y llamamos D = {f ∈ L2 (R) : x · f (x) ∈ L2 (R)}.
Probar que el operador T : H → H definido por T f (x) = xf (x) con
dominio D es autoadjunto. [Este es el llamado operador posición
en Mecánica Cuántica.]
Resp.: Veamos que D es denso en L2 (R). Para ello, basta observar
que D contiene al conjunto de las funciones con soporte compacto y
que este conjunto es denso en L2 (R).
Veamos a continuación que T es simétrico:
Z
Z
hT f, gi =
xf (x) g(x)dx =
f (x) · xg(x)dx = hf, T gi, ∀f, g ∈ D.
R
R
Esto implica que T ⊂ T ∗ (ver proposición 1.6).
Por último, comprobaremos que D(T ∗ ) ⊂ D(T ):
Sea g ∈ D(T ∗ ) y llamemos g ∗ = T ∗ g. Por definición de adjunto,
Z
Z
f (x) g ∗ (x)dx.
∀f ∈ D(T ),
xf (x) g(x)dx =
R
R
318
Si tomamos f (x) = χ[α,x0 ] , la igualdad anterior queda
Z
x0
Z
x0
g ∗ (x)dx
x g(x)dx =
α
α
y, derivando, x0 g(x0 ) = g ∗ (x0 ) para casi todo x0 . Esto implica que
g ∈ D y T ∗ g(x) = xg(x).
De lo anterior se deduce que T es autoadjunto.
4. Sea H = L2 (R) y D = {f ∈ L2 (R) : f es absolutamente continua
en todo intervalo finito y f 0 ∈ L2 (R)}. Probar que el operador
T : H → H definido en D por T f (x) = −if 0 (x) es autoadjunto.
[Este es el operador momento en Mecánica Cuántica.]
Resp.: Definimos para cada n la función continua


si x ∈ [α, x0 ]
1
fn (x) = 0
si x ≤ α − 1/n ó x ≥ x0 + 1/n


recta en el resto.
Las combinaciones lineales de funciones de la forma de fn con diferentes valores de α, x0 y n son densas en L2 (R). Por tanto, D es denso
en H.
Para probar que T es simétrico, sea g ∈ D. Entonces, ∀f ∈ D, integrando por partes obtenemos:
Z
a
b
b
−if (x) g(x)dx = −if (x) g(x)a +
0
Z
b
f (x)[ −ig 0 (x)]dx.
a
Como f (x) g(x) es integrable en R, se deduce que
lı́m
a→−∞,b→∞
b
f (x) g(x)a =
0y
Z
hT f, gi =
Z
0
−if (x) g(x)dx =
f (x)[ −ig 0 (x)]dx = hf, T gi.
R
R
Esto implica que g ∈ D(T ∗ ) y T ∗ g(x) = −ig 0 (x), es decir T ⊂ T ∗ .
Sólo falta comprobar, al igual que en el ejercicio anterior, que D(T ∗ ) ⊂
D. Sea para ello g ∈ D(T ∗ ) y llamemos g ∗ = T ∗ g. Como sabemos,
Z
Z
0
−if (x) g(x)dx =
f (x) g ∗ (x)dx, ∀f ∈ D.
R
R
319
Eligiendo las funciones fn anteriores, la igualdad anterior se escribe
como:
Z α
Z x0 +1/n
Z
−i g(x)dx − n
n
−i g(x)dx =
fn (x) g ∗ (x)dx.
α−1/n
x0
R
Haciendo n → ∞, obtenemos:
Z x0
g ∗ (x)dx para casi todos α y x0 .
−i g(α) − g(x0 ) =
α
Por la desigualdad de Schwarz, se deduce que g ∗ es integrable sobre
cualquier intervalo finito. Entonces g(x0 ) es absolutamente continua
en x0 sobre cualquier intervalo finito y, por tanto, −ig 0 (x0 ) = g ∗ (x0 )
para casi todo x0 . Esto implica que g ∈ D y T ∗ g(x) = −ig 0 (x).
5. Probar que el operador T1 f (x) = if 0 (x) es simétrico en D(T1 ) =
{f ∈ L2 [0, 1] : f es absolutamente continua, f (0) = f (1) = 0, f 0 ∈
L2 [0, 1]} pero no es autoadjunto.
Resp.: Veamos que T1∗ = T2 donde T2 f (x) = if 0 (x) tiene dominio
D(T2 ) = {f ∈ L2 [0, 1] : f es absolutamente continua y f 0 ∈ L2 [0, 1]}.
Debido a que D(T1 ) = L2 [0, 1], existe el adjunto T1∗ . Si g ∈ D(T1∗ ) y
llamamos g ∗ = T1∗ g, entonces
Z 1
Z 1
∀f ∈ D(T1 ) :
if 0 (x) g(x)dx =
f (x) g ∗ (x)dx.
0
0
R1
Si integramos
por partes, 0 f (x) g ∗ (x)dx = −
R
x
G∗ (x) = 0 g ∗ (s)ds.
R1
Como f (1) = 0 f 0 (x)dx = 0, entonces
1
Z
R1
0
f 0 (x) G∗ (x)dx, donde
f 0 (x)[ G∗ (x) + i g(x) + c]dx = 0, ∀f ∈ D(T1 ), ∀c.
0
Rx
R1
Por otra parte, ∀h ∈ L2 [0, 1], la función H(x) = 0 h(s)ds−x 0 h(s)ds
está en D(T1 ). Para esta función se tiene:
Z 1n
Z 1
o
h(x) −
h(s)ds G∗ (x) + i g(x) + c dx = 0.
0
0
Eligiendo c de modo que
R1
0
[G∗ (x)−ig(x)+c]dx = 0, resulta la igualdad
320
R1
∗ (x) + i g(x) + c dx = 0. Al ser h arbitrario, G∗ (x) =
G
h(x)
R0x ∗
∗
0 g (s)ds = ig(x) − c. Por tanto, g ∈ D(T2 ) y T2 g = g , lo que
∗
prueba que T1 ⊂ T2 .
Es claro también, integrando por partes, que T2 ⊂ T1∗ , lo que completa
la prueba.
6. Sea T : D(T ) ⊂ H → H un operador lineal con dominio denso en
H . Probar la siguiente equivalencia:
i) T es clausurable
ii) D(T ∗ ) = H .
Resp.: La implicación i) =⇒ ii) corresponde a la proposición 1.8.b).
El recı́proco se deduce del apartado 2 del corolario 1.9 (basta observar
que T ⊂ T ∗∗ y que T ∗∗ es cerrado).
7. A la ecuación diferencial f 00 − f = g , siendo g ∈ L2 [0, 1] una
función conocida, se le asocian los tres problemas de contorno
siguientes:
a) f (0) = f (1) = 0.
b) f 0 (0) = f 0 (1) = 0.
c) f (0) = f (1) y f 0 (0) = f 0 (1).
Mostrar que los tres problemas tienen solución única f tal que
f 0 es absolutamente continua y f 00 ∈ L2 [0, 1].
Resp.: En el espacio de Hilbert H = L2 [0, 1] definimos los operadores
Tk f = if 0 (k = 1, 2, 3), con dominios
D(T1 ) = {f ∈ H : f es absolutamente continua y f 0 ∈ H}
D(T2 ) = {f ∈ D(T1 ) : f (0) = f (1)} ⊂ D(T1 )
D(T3 ) = {f ∈ D(T2 ) : f (0) = f (1) = 0} ⊂ D(T2 ).
Entonces T3 ⊂ T2 ⊂ T1 y además T1∗ = T3 , T2∗ = T2 y T3∗ = T1 (como
observábamos en el ejemplo de la página 322).
321
a) Sea f ∈ D(T3∗ T3 ); entonces (I + T3∗ T3 )f = f + T1 T3 f = f − f 00 .
Como T3 es cerrado (pues T3 = T1∗ ), y D(T3 ) = H, entonces I +T3∗ T3 :
D(T3∗ T3 ) → H es biyectivo (teorema 1.13). Ası́ pues, ∀g ∈ H, existe
un único f ∈ D(T3∗ T3 ) tal que (I + T3∗ T3 )f = −g, es decir f 00 − f = g.
Ahora bien, por ser f ∈ D(T3∗ T3 ), f ∈ D(T3 ) y T3 f ∈ D(T3∗ ), es decir
f (0) = f (1) = 0, f 0 es absolutamente continua y f 00 ∈ H, lo que
resuelve el problema a).
b) Sea ahora f ∈ D(T1∗ T1 ); nuevamente, (I + T1∗ T1 )f = f + T3 T1 f =
f − f 00 . El teorema 1.13 prueba también que el operador I + T1∗ T1 :
D(T1∗ T1 ) → H es biyectivo. Ası́ pues, ∀g ∈ H, existe un único f ∈
D(T1∗ T1 ) tal que (I + T1∗ T1 )f = −g, es decir f 00 − f = g. Dicha solución
verifica ahora que f ∈ D(T1 ) y T1 f ∈ D(T1∗ ), lo que corresponde a las
condiciones f 0 (0) = f 0 (1) = 0, f 0 absolutamente continua y f 00 ∈
L2 [0, 1].
c) Consideramos en este caso f ∈ D(T2∗ T2 ). Repitiendo el proceso
seguido en los dos casos anteriores se prueba la existencia de solución
para este problema.
8. Dada g ∈ L2 (R), probar que la ecuación diferencial f 00 − f = g
tiene solución única f ∈ L2 (R) tal que f 0 , f 00 ∈ L2 (R) y f, f 0 son
absolutamente continuas.
Mediante cálculo directo, encontrar la fórmula
Z
Z
1 x t−x
1 ∞ x−t
f (x) = −
e g(t)dt −
e g(t)dt
2 −∞
2 x
para determinar la solución de la ecuación.
Resp.: Consideramos el operador T f = if 0 con dominio el conjunto
de funciones absolutamente continuas en un intervalo cerrado de R y
cuya derivada está en L2 (R).
Como dicho dominio es denso en L2 (R) y T es autoadjunto, el teorema
1.13 prueba que I + T 2 : D(T 2 ) → L2 (R) es biyectivo. Ası́ pues,
dado g ∈ L2 (R), existe un único f ∈ D(T 2 ) tal que (I + T 2 )f =
−g, es decir f 00 − f = g. Como f ∈ D(T ) y f 0 ∈ D(T ), la solución
f es absolutamente continua y f 0 ∈ L2 (R), ası́ como también f 0 es
absolutamente continua y f 00 ∈ L2 (R).
Para resolver explı́citamente la ecuación f 00 − f = g, buscamos en
primer lugar la solución general de la ecuación homogénea asociada
322
f 00 − f = 0, lo que da el conjunto y = C1 ex + C2 e−x , con C1 , C2
constantes arbitrarias.
A continuación aplicamos el método de variación de constantes para
resolver la ecuación no homogénea, es decir resolvemos el sistema
C10 (x)ex + C20 (x)e−x = 0
C10 (x)ex − C20 (x)e−x = g(x)
el cual tiene como solución C10 (x) = (1/2)g(x)e−x , C20 (x) = −(1/2)g(x)ex .
La solución general de la ecuación queda pues de la forma indicada en
el enunciado.
9. Sea E una medida espectral arbitraria (ver definición 3.2). Probar que |Ex,y (∆)|2 ≤ Ex,x (∆)Ey,y (∆), ∀x, y ∈ H .
Resp.: Teniendo en cuenta que E(∆) es una proyección ortogonal, por
la desigualdad de Cauchy-Schwarz, obtenemos:
|hE(∆)x, yi|2 = |hE(∆)x, E(∆)yi|2
≤ kE(∆)xk2 · kE(∆)yk2 = hE(∆)x, E(∆)xi · hE(∆)y, E(∆)yi
= hE(∆)x, xi · hE(∆)y, yi.
10. Sea T un operador simétrico con dominio denso. Probar que el
operador U : R(T + iI) → R(T − iI) definido por
U = (T − iI)(T + iI)−1
(llamado también transformada de Cayley de T ) es isométrico.
Resp.: Veamos en primer lugar que existe (T + iI)−1 y es acotado
(como operador definido en R(T + iI)). Para ello basta observar la
siguiente desigualdad, que es consecuencia de la proposición 1.12:
k(T + iI)xk2 = kT xk2 + kxk2 ≥ kxk2 , ∀x ∈ D(T ).
Para probar que U es isométrico, sean x, y ∈ D(U ). Entonces ∃f, g ∈
D(T ) tales que x = (T + iI)f , y = (T + iI)g. Ası́ pues,
hU x, U yi = h(T − iI)f, (T − iI)gi
= hT f, T gi + hT f, −igi + h−if, T gi + h−if, −igi
= hT f, T gi + ihf, T gi − ihT f, gi + hif, igi
= hT f, T g + igi + hif, T g + igi = hT f + if, T g + igi = hx, yi.
323
11. En el espacio `2 se define el operador V por V (α1 , α2 , . . . ) =
(0, α1 , α2 , . . . ). Probar que V es la transformada de Cayley de
un operador simétrico T con ı́ndices de defecto 0 y 1, donde, por
definición, los ı́ndices de defecto de un operador simétrico T son
las dimensiones de R(T + iI)⊥ y R(T − iI)⊥ . Hallar una expresión
de T .
Resp.: (•) Veamos en primer lugar que V es isometrı́a:
X
X
|αn |2 = kαk22 .
|αn |2 y kV αk22 =
∀α ∈ `2 : kαk22 =
n∈N
n∈N
Sin embargo, V no es unitario pues el elemento α = (1/n)n∈N está en
`2 pero no está en el rango de V .
(•) Probaremos a continuación que I − V es inyectiva. En efecto, si
α ∈ N (I − V ), entonces α = V α, es decir α1 = 0, αn+1 = αn , ∀n ∈ N,
de donde α = 0.
(•) De las condiciones anteriores se deduce la existencia de un operador
simétrico T cuya transformada de Cayley es V , T = i(I +V )(I −V )−1 ,
y D(T ) = R(I − V ).
(•) Calcularemos a continuación los ı́ndices de defecto de T :
Como D(V ) = `2 , R(T + iI) = `2 de donde dim R(T + iI)⊥ = 0.
P
2
Por otra parte, como R(V ) = {(0, α1 , α2 , . . . ) :
n∈N |αn | < ∞},
⊥
entonces R(V ) está generado por el elemento (1, 0, 0, . . . ). Teniendo
en cuenta que R(V ) = R(T − iI), es evidente que dim R(T − iI)⊥ = 1.
(•) Para obtener una expresión explı́cita de T , observemos que
(I − V )(α1 , α2 , . . . ) = (α1 , α2 − α1 , . . . ). Por tanto,
−1
(I − V )
(α1 , α2 , . . . ) = (α1 , α1 + α2 , . . . ,
n
X
αk , . . . )
k=1
(I + V )(α1 , α2 , . . . ) = (α1 , α1 + α2 , . . . , αn−1 + αn , . . . )
=⇒ T (α1 , α2 , . . . ) = i(I + V )(I − V )−1 (α1 , α2 , . . . )
n−1
X
= i(α1 , α2 + 2α1 , . . . , αn + 2
αk , . . . ),
k=1
con D(T ) = {(αn )n∈N : |α1 |2 +|α1 +α2 |2 +· · ·+|
324
Pn
2
k=1 αk | +. . .
< ∞}.
12. Sea T un operador autoadjunto con dominio denso en H y Rz =
(T − zI)−1 el operador resolvente definido en el conjunto de valores {z ∈ C : ∃(T − zI)−1 , R(T − zI) = H}. Probar:
a) kRz xk ≤ (1/|β|)kxk si β = Im z 6= 0.
b) Rz2 − Rz1 = (z2 − z1 )Rz2 Rz1 , ∀z1 , z2 ∈ ρ(T ).
c) (Rz )∗ = R z .
Resp.: a) A partir de la igualdad
k(T − zI)xk2 = β 2 kxk2 + k(T − αI)xk2 , ∀x ∈ D(T ), z = α + iβ,
si hacemos y = (T − zI)x, resulta kyk2 ≥ β 2 k(T − zI)−1 yk2 .
b) Es evidente que
R z2 − R z1
= Rz2 (T − z1 I)Rz1 − Rz2 (T − z2 I)Rz1
= Rz2 [(T − z1 I) − (T − z2 I)]Rz1 = (z2 − z1 )Rz2 Rz1 .
De esta relación se deduce la conmutatividad Rz1 Rz2 = Rz2 Rz1 , ∀z1 , z2 ∈
ρ(T ).
c) Como D(Rz ) = H, existe (Rz )∗ . Además, ∀x ∈ D(Rz ), y ∈ D(R z ):
hRz x, yi = hRz x, (T − zI)R z yi = h(T − zI)Rz x, R z yi
= hx, R z yi =⇒ R z = (Rz )∗ .
TEMAS COMPLEMENTARIOS.
1. Operadores de multiplicación y derivación ([AG], [Kr]).
2. Semigrupos de operadores ([Ru]).
3. Operadores no acotados en Mecánica Cuántica ([Kr]).
4. Operadores cerrados y clausurables. Teorema de la aplicación abierta
para operadores no acotados ([CC]).
325